Seismic earth pressures on f l exible cantilever retaining walls with deformable inclusions

Ozgur L.Ertugrul,Aurelian C.Trandaf i r

aDepartment of Civil Engineering,Mersin University,Ciftlikkoy 33343,Turkey

bFugro GeoConsulting,Inc.,Houston,TX 77081,USA

Seismic earth pressures on f l exible cantilever retaining walls with deformable inclusions

Ozgur L.Ertugrula,*,Aurelian C.Trandaf i rb

aDepartment of Civil Engineering,Mersin University,Ciftlikkoy 33343,Turkey

bFugro GeoConsulting,Inc.,Houston,TX 77081,USA

A R T I C L E I N F O

Article history:

Received 10 April 2014

Received in revised form

9 July 2014

Accepted 15 July 2014

Available online 26 August 2014

Cantilever retaining wall

Deformable geofoam panel

1-g shaking table tests

Dynamic earth pressure

Polystyrene

Flexibility ratio

Analytical approach

In this study,the results of 1-g shaking table tests performed on small-scale fl exible cantilever wall models retaining composite back fi ll made of a deformable geofoam inclusion and granular cohesionless material were presented.Two different polystyrene materials were utilized as deformable inclusions. Lateral dynamic earth pressures and wall displacements at different elevations of the retaining wall model were monitored during the tests.The earth pressures and displacements of the retaining walls with deformable inclusions were compared with those of the models without geofoam inclusions. Comparisons indicated that geofoam panels of low stiffness installed against the retaining wall model affect displacement and dynamic lateral pressure pro fi le along the wall height.Depending on the inclusion characteristics and the wall fl exibility,up to 50%reduction in dynamic earth pressures was observed.The ef fi ciency of load and displacement reduction decreased as the fl exibility ratio of the wall model increased.On the other hand,dynamic load reduction ef fi ciency of the deformable inclusion increased as the amplitude and frequency ratio of the seismic excitation increased.Relative fl exibility of the deformable layer(the thickness and the elastic stiffness of the polystyrene material)played an important role in the amount of load reduction.Dynamic earth pressure coef fi cients were compared with those calculated with an analytical approach.Pressure coef fi cients calculated with this method were found to be in good agreement with the results of the tests performed on the wall model having low fl exibility ratio.It was observed that deformable inclusions reduce residual wall stresses observed at the end of seismic excitation thus contributing to the post-earthquake stability of the retaining wall.The graphs presented within this paper regarding the dynamic earth pressure coef fi cients versus the wall fl exibility and inclusion characteristics may serve for the seismic design of full-scale retaining walls with deformable polystyrene inclusions.

©2014 Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.Production and hosting by Elsevier B.V.All rights reserved.

1.Introduction

Studies on the reduction of dynamic earth pressures of retaining walls have gained signif i cant importance during this decade. Within these studies,utilization of geofoam inclusions appears as an innovative approach to reduce the earth pressures on retaining walls.Several studies focused on the potential load reduction eff iciency of geofoam inclusions,indicating that the reduction performance of the geofoam inclusions depends on characteristics of the dynamic excitation,and mechanical characteristics of the backf i ll and deformable material.

Athanasopoulos et al.(2007),Bathurst et al.(2007),Zarnani and Bathurst(2009),and Ertugrul and Trandaf i r(2011)investigated the reduction of dynamic earth pressures of yielding rigid walls by compressible inclusions.Subsequently,Trandaf i r and Ertugrul (2011)discussed the inf l uence of geofoam inclusions on reducing lateral dynamic earth pressure and displacements of a yielding gravity retaining wall subjected to a real earthquake excitation. Athanasopoulos-Zekkos et al.(2012)used deformable inclusions to reduce the seismic incremental earth pressures and displacements of yielding gravity type earth retaining walls.

In a recent study,Ertugrul and Trandaf i r(2013)discussed the results of 1-g static loading tests performed on cantilever retaining walls with EPS and XPS geofoam inclusions.In this study,onlystatic load reduction eff i ciency of geofoamwas investigated.Based on the static test results,a f i nite element model was analyzed and the outputs of the numerical model were validated using test data. Parametric analyses were performed to investigate the effect ofdifferent backf i ll and geofoam characteristics as well as structural performances of the cantilever walls.Formulas were proposed to estimate the static load reduction eff i ciency of geofoam inclusions placed against retaining walls with different characteristics.In the currentinvestigation,dynamicresponseofcantileverearth retaining walls with deformable inclusions subjected to dynamic loads are discussed based on 1-g shaking table test results.

2.Methodology of the study

The present study focuses on the reduction of dynamic earth forces of yielding cantilever retaining walls caused by deformable geofoam inclusions.Deformable inclusion properties,f l exibility of the retaining wall,granular backf i ll characteristics and the excitation parameters signif i cantly increase the complexity of the mechanism of dynamic load reduction mechanism induced by the deformable panels of geofoam.Under such circumstances,physical testing with shaking table serves as a versatile tool to investigate this complex soil-geofoam-structure interaction.In the present study,the results of 1-g shaking table tests performed on smallscale f l exible cantilever wall models using either the granular backf i ll or the deformable geofoam panel-granular backf i ll system are presented and discussed.Tests were conducted in a state-ofthe-art laminar container to reduce the disturbance of the model response from wave ref l ections encountered in dynamic tests performed in the rigid containers.Inf l uences of wall stiffness, geofoam type,inclusion thickness and seismic excitation characteristics(frequency and amplitude)on the dynamic earth pressures and wall displacements were investigated.

Results of the current study were also compared with those of analytical Steedman—Zeng methodology(Steedman and Zeng, 1990),which was validated using data obtained from physical tests performed on centrifuge facility.

3.Physical tests

The 1-g physical tests performed on small-scale geotechnical models,an inexpensive and eff i cient way to investigate the behavior of the prototype qualitatively.However,these tests have their own disadvantages,e.g.the requirements of the dimensional similitude theory may not be fully fulf i lled in 1-g physical model tests.Some published papers(Hazarika et al.,2003;Bathurst et al., 2007)also discussed 1-g shaking table test results without mentioning prototype dimensions and the dimensional similitude relationships.In content,dynamic centrifuge tests are more successful in satisfying the similitude relationships between the prototypeandthemodel(Wangetal.,2005;Wang,2012). Nevertheless,dynamic 1-g tests can provide a source of reliable data for supporting numerical modeling and back analysis(Wood, 2004).

Fig.1.Cross-sectional view of the model conf i gurations.(a)Control test;(b)Wall with geofoam inclusion.

Fig.2.Typical cyclic stress—strain loops for EPS15(f=3 Hz;N=10 cycles).(a) Δ(σ1-σ3)cyclic=3 kPa,(b)Δ(σ1-σ3)cyclic=12 kPa.

Physical tests were conducted using a rectangular laminar sand container available in the Department of Civil Engineering at the Middle East Technical University.The uniaxial container with dimensions of 1.0 m×1.5 m×1.0 m(length×width×height) consists of laminar frames,low friction linear and ball bearings, guide walls to limit vertical dilatational movements of the frames and a thin membrane made of rubber to prevent material leakage when the laminar frames are moving.

Pressure and displacement transducers weremounted along the wall height to monitor pressures and displacements of the wall stem.Accelerometers were placed at different heights within the backf i ll and on the wall to monitor horizontal and vertical accelerations.A cross-sectional view of the test set-up and positions of the transducers are depicted in Fig.1.The model walls are composed of steelwith dimensions of 700 mm×980 mm×(2-4-5-8)mm(height×length×thickness)rigidly welded to a steel basewithdimensionsof980mm×500mm×8mm (length×width×thickness).The connection of the wall stem to the wall foundation was achieved by welding.Signals from the transducers were recorded by a digital data acquisition hardware capable of 100 kHz sampling at each channel and signal conditioning elements for the required channels.

Fig.3.Normalized Young’s modulus(E/E0)in relation to the cyclic axial strain amplitude((σ1-σ3)static=15 kPa andΔ(σ1-σ3)cyclic=3—14 kPa).

4.Material characteristics

The geotechnical properties of the dry cohesionless backf i ll material used in the tests was described by Ertugrul and Trandaf i r (2011).The granular material is classif i ed as poorlygraded sand(SP) which consists of highly angular grains.The maximum and minimum void ratios of the model sand were determined as 0.745 and 0.436,respectively,according to the procedure described by Head (1992).Specif i cgravity(Gs)wasdeterminedas2.66from thetestsperformedfollowingASTMD854-83procedures. Consolidated-drained triaxial tests yielded an internal friction angle and dilatancy angle of 43.5°and 22.5°,respectively,for an effective conf i ning stress range of 5—15 kPa.

The densities of EPS and XPS geofoam materials used as deformable panels in the physical tests were determined as 15 kg/ m3and 22 kg/m3,respectively.Low-densitygeofoam products were carefully selected for this study in order to provide a low stiffness buffer between thewall and the cohesionless backf i ll,thus allowing for soil lateral displacements induced by the compression of the deformable zone at very low conf i ning stresses.

Static and cyclic triaxial tests were carried out on geofoam samples to determine the stress—strain relationship.Cylindrical specimens having a height to diameter ratio of 2 were extracted from EPS and XPS panels by computer-controlled laser cutters at ACH Foam Technologies LLC,Salt Lake City,Utah.The uniaxial compression tests on geofoam for EPS15 and XPS22 provided yield stresses of 39 kPa and 131 kPa,respectively,at a strain rate of 10-4min-1.The strain rate was consistent with the loading rate of the geofoam panels during the backf i lling process of the 700-mm high retaining wall models in the physical tests.

According to the triaxial test results,EPS geofoam basically exhibits bi-linear stress—strain behavior with strain hardening occurring at 2%axial strain.Elastic modulus(Ei)representing the linear elastic portion was determined as 1500 kPa from monotonicloading tests.The measured elastic modulus of the EPS used in the current study is signif i cantly lower than that estimated by the relationship suggested by Horvath(1995).One important cause of the low elastic modulus reported in the current study is the low strain rate(10-4min-1)that has been adopted in the compression tests performed.Most of the relationships in the literature between the elastic modulus and the density of the geofoam were based on the monotonic test results performed with a customary strain rate of 10-1min-1(Koerner,2005).Duskov(1997)reported that loading rate signif i cantly affects the stiffness of the EPS geofoam.

Table 1A summary of the test parameters.

XPS geofoam exhibits a well-def i ned yield point in association with strain softening after yielding.Elastic modulus representing the linear elastic portion was determined as 5580 kPa.The triaxial test results also revealed that an increase in the conf i ning stresses causes a decrease in the elastic modulus and yields deviatoric stress of geofoam.

Stress-controlled cyclic triaxial tests were performed on EPS15 and XPS22 samples to determine the dynamic modulus(Edyn)and the maximum axial strain(εmax)under dynamic loads.During the tests,cyclic component of the axial stress remained below the static conf i ning stresses initially applied to the samples.Fig.2 shows the viscoelastic stress—strain response of EPS geofoam at different cyclic deviatoric stress levels.Based on the data obtained from cyclic triaxial tests,the Young’s moduli(E)of the geofoam at different axial strains were normalized with initial modulus(E0)to develop E/E0degradation curves for EPS and XPS geofoams in relation to the cyclic axial strain amplitude,as shown in Fig.3.

In the tests,cyclic axial strain amplitudes(εac)up to about 0.50% were observed.According to the results proposed by Trandaf i r and Erickson(2012),geofoam exhibits visco-elasto-plastic behavior after exceeding threshold of axial strain amplitude of 0.54%.Hence, the dynamic properties of the EPS and XPS geofoams reported in this study are representative for the viscoelastic behavior of these materials.The initial Young’s moduli of EPS15 and XPS22 corresponding to a cyclic strain amplitude εac=0.01%were estimated as 4745 kPa and 8907 kPa,respectively,using the following equation proposed by Trandaf i r and Erickson(2012):

where E0andρare expressed in kPa and kg/m3,respectively.The initial Young’s moduli estimated by Eq.(1)were found to be in agreement with the results of the laboratory tests performed in this study.Trandaf i r and Erickson(2012)indicated that results from cyclic uniaxial compression tests performed on EPS geofoam reveal insignif i cant variation in the Young’s modulus for cyclic axial strain amplitudes of up to 5×10-4.Thus,the measured Young’s modulus values at cyclic axial strain amplitudes not greater than 5×10-4in cyclic uniaxial compression tests may be appropriate to describe the small strain elastic behavior of geofoam.

5.Test procedure

Fig.4.Retaining wall model(dw=524)without deformable inclusion;(a)Before the dynamic phase;(b)After 0.1 g-4 Hz excitation;(c)After 0.4 g-8 Hz excitation;(d)After 0.7 g-10 Hz excitation.

The instrumented retaining wall models were placed on the 20-cm thick compacted layer of sand.During the backf i lling process, the wall model was kept f i xed against horizontal movements by means of lateral supports.Backf i ll was constituted of 10-cm lifts by dry pluviation,a commonly used method to reconstitute granular materials representative of some initial state(Okamoto and Fityus, 2006).To make use of dry pluviation technique,a steel shutter and diffuser screen having the same dimensions with the laminar container were manufactured.Based on the test results presented by Okamoto and Fityus(2006),hole spacing of the shutter and diffuser screen were selected as 60 mm and 2.36 mm,respectively, in order to obtain relative densities between 70%and 75%by raining procedure.At the end of the backf i lling process,the data acquisition equipment was used to monitor wall pressures on the non-yielding wall(lateral restraints were presented).The dataacquisition continued during the removal of the restraints accomplished by the slow unloading of the mechanical jack located between the wall model and the sides of the container.Lateral earth pressures and wall movements were monitored until no further wall movements and pressure redistribution occurred.The tests involving compressible geofoam inclusions were carried out following the same procedure.However,EPS and XPS geofoam panels were installed between the wall model and the backf i ll prior to the pluviation.Direct shear tests were performed to determine the interface friction between the geofoam and the granular material.The friction coeff i cient of the contact plane between the geofoam and the granular backf i ll was found as 0.13 since the surfaces of the geofoam panels used in the current study were covered with plastic tape to reduce the friction between the soil and the geofoam.With decreasing frictional force at the geofoam—backf i ll interface,the loading axis of the earth thrust becomes closer to horizontal.In the shaking table tests,harmonic displacements matching the following target sinusoidal acceleration-time history were applied to the base of the laminar container by means of dynamic actuator:

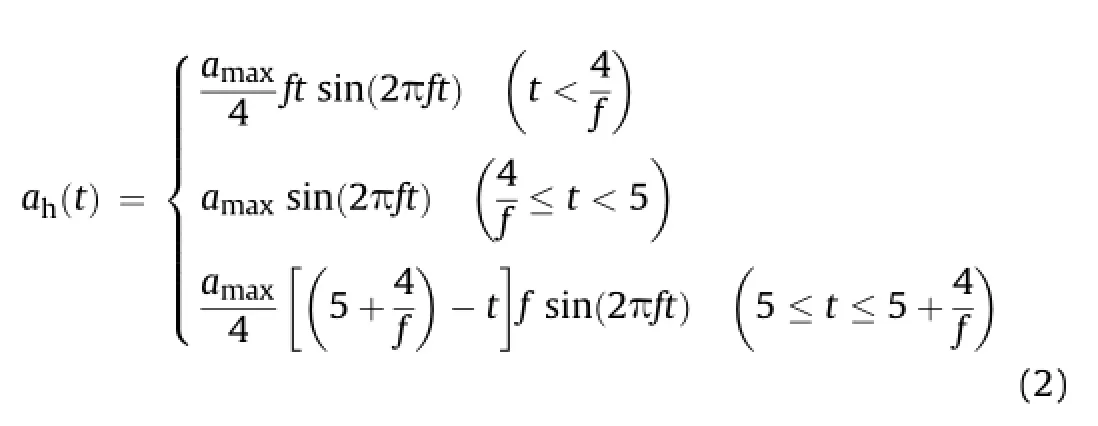
where t is the time,f is the frequency of the excitation,and amaxis the acceleration amplitude.Although the application of random earthquake excitations in physical modeling studies is considered more realistic,Bathurst and Hatami(1998)and Matsuo et al.(1998) reported that simple harmonic base excitations can cause more aggressive impact on the physical model when compared with the effect of a real earthquake excitation with similar predominant frequency and amplitude.Additionally,application of harmonic base motion allows the physical models to be excited in the same controlled way by enabling more accurate comparisons to be made regarding the effect of different input parameters investigated in this study.A summary of the test parameters is listed in Table 1.

Retaining wall models having different stem thicknesses were used to investigate the inf l uence of relative f l exibility of the retaining structure on the seismically induced earth pressures and the performance of deformable geofoam inclusions.Plane strain relative f l exibility ratio(dw)of a retaining wall is considered as the primary parameter affecting the response of the cantilever wallbackf i ll system(Veletsos and Younan,1997)and is expressed in a dimensionless form as

where G is the shear modulus of the backf i ll,H is the wall height,Ewis the Young’s modulus of the wall,twis the wall thickness,andνwdenotes the Poisson’s ratio of the material.Relative f l exibility ratios for four model walls were determined as 128,524,1024 and 8197 when calculated using Eq.(3).

6.Discussion of the test results

Fig.5.Retaining wall model(dw=524)with EPS15 deformable inclusion having ti/H=0.14.(a)Before the dynamic phase;(b)After 0.1 g-4 Hz excitation;(c)After 0.4 g-8 Hz excitation;(d)After 0.7 g-10 Hz excitation.

Residual wall displacements and surface settlements of the backf i ll at the end of different seismic excitation phases aredepicted in Figs.4 and 5.It is indicated that horizontal displacements and back fi ll settlements increase as the excitations with higher amplitude and frequency were applied to the model.EPS15 geofoam panel having a relative thickness(i.e.ratio of panel thickness,ti,to wall height,H)ti/H=0.14 caused a signi fi cant increase in the back fi ll settlement as a result of the compressive deformations of the geofoam panel.

In the test series without geofoam panels,the surface settlements at the end of the test were signi fi cantly lower when compared with those of the geofoam tests.It was observed that the fl exural wall deformations and the reduction in the back fi ll volume due to dynamic densi fi cation are the primary factors causing settlement for the tests without geofoam.However,installation of a compressible element between the wall stem and the granular back fi ll introduces another factor,i.e.compressible deformations of the geofoam layer,which causes additional surface settlements. Horvath(2010)de fi ned a dimensionless parameter(λ)called the normalized compressible inclusion stiffness:

Fig.6.Evolution of the dynamic wall pressures monitored at the wall base (amax=0.3 g,f=4 Hz).

where Patmis the atmospheric pressure,in the same units as E,used to makeλdimensionless.Parameter“λ”is dependent on H/tias can be observed from the given formula.In the current investigation, the authors def i ned ti/H as the relative thickness and used this parameter in the discussions.During the tests,it was observed that the settlement in the vicinity of the wall increases as ti/H increases.

In the dynamic tests,the granular backf i ll subjected to dynamic base excitation was densif i ed,causing higher lateral stresses in the backf i ll compared with the initial condition.As the lateral loads of the geofoam buffer increases permanently due to soil densif i cation, compressive deformations of the geofoam panels continuously increase,causing progressive vertical backf i ll settlements in the vicinity of the wall.While the compressive deformations in the geofoam panels increase,higher volume of granular backf i ll moves in the horizontal direction towards the wall.This causes additional vertical backf i ll settlements concentrated in the vicinity of the wall. As the relative thickness ratio(ti/H)of the geofoam inclusion increases,theadditionalverticalsettlementsareinducedby compressive deformations of the geofoam.

6.1.Dynamic wall pressures and lateral displacements

In Fig.6,the total dynamic earth pressures at the depth z=H (i.e.wall base)were compared for Type-III wall models(dw=524) subjected to a base excitation characterized by amax=0.3 g and f=4 Hz.Initial static stresses as well as the dynamic incremental stresses for the walls with EPS15 geofoam inclusions were found to be lower than those of the model without deformable inclusion. The increments of dynamic stresses for Type-III-E7 and Type-IIIE14 models(EPS15 inclusion with ti/H=0.07 and ti/H=0.14, respectively)were signif i cantly lower compared with the control case of the wall without geofoam inclusion(Type-III-N).

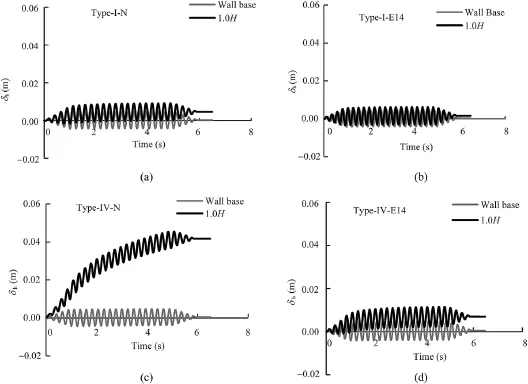
Fig.7.Evolutions of wall displacements for(a)Type-I-N;(b)Type-I-E14(dw=128);(c)Type-IV-N;(d)Type-IV-E14(dw=128).

Fig.8.Evolution of the total dynamic thrust for(a)Type-I-N;(b)Type-I-E14(dw=128);(c)Type-IV-N;(d)Type-IV-E14(dw=8197).

The evolutions of lateral displacements at the wall top during dynamic phase(amax=0.3 g and f=4 Hz)for the most rigid(Type-I, dw=128)and the most f l exible models(Type-IV,dw=8197)are compared in Fig.7.The horizontal displacements monitored at the top(indicated with bold lines)of the model Type-I(Fig.7a)are signif i cantly lower than those observed for the more f l exible model wall Type-IV(Fig.7c).Residual wall displacements(δres)increase as wall f l exibility ratio increases.EPS15 geofoam inclusions with ti/ H=0.14 signif i cantly reduce the dynamic incremental and residual wall displacements(Fig.7b and d).

Based on the comparisons of the lateral dynamic pressure and wall displacements with different f l exibility ratios,it can be noted that the earth pressure against the rigid walls was reduced by the within-backf i ll deformations induced by the lateral compression of the low stiffness inclusion.The widespread backf i ll settlements were considered to be an indicator of the compressive deformations of the geofoam panel.This positive effect of the deformable geofoam panels also reduces the f l exural displacements of the wall stem in association with the load reduction behavior.Pressures and displacements of the walls with XPS geofoam panel were not presented in Figs.6 and 7.However,it can be said that the XPS deformable panels have slightly low eff i ciency compared with the performance of the EPS geofoam panels.

The evolution of the total dynamic lateral force of model walls Type-I and Type-IV is depicted in Fig.8.Wall f l exibility has an effect on the residual earth force(Pres)as well as on the dynamic component(ΔPdyn)of thetotalthrust(Fig.8a andc).EPS15 geofoam with ti/H=0.14 provides signif i cant reduction in PresandΔPdynfor both of the models(Fig.8b and d).

Fig.9.The parameters used in the calculation of the dynamic earth forces according to Steedman—Zeng method(1990).

Fig.10.Normalized earth pressure prof i les calculated with Steedman—Zeng method (amax=0.3 g and f=5 Hz).

6.2.Comparisons of the test data with the results obtained by Steedman—Zeng method

One of the important studies addressing the evaluation of dynamic lateral earth pressures of f i xed base cantilever retaining walls was presented by Steedman and Zeng(1990).In this study, the authors proposed an analytical methodology which took into account the shear wave velocity distribution within the backf i ll, thus allowing for a phase difference and variable acceleration prof i le in a prototype.Centrifuge test data exhibited a good agreement with the results obtained by the analytical methodology well known as Steedman—Zeng(S—Z)method.

The parameters used in the calculation of seismic forces with the analytical approach suggested by Steedman and Zeng(1990) are presented in Fig.9.The harmonic base excitation is written as

where khis the horizontal acceleration amplitude,Vsis the shear wave velocity of the backf i ll,ωis the angular frequency of the base shaking,and z is the elevation measured from the wall top.For a typical f i xed base cantilever wall,the horizontal inertia force Qhactingon a horizontalelement(thickness of dz)of thefailurewedge within the backf i ll is given by

whereρis the density of the backf i ll,andαis the inclination angle of wedge with the horizontal direction.The total dynamic thrust is calculated with the following equation considering the equilibrium of the forces acting on the wedge shown in Fig.9:

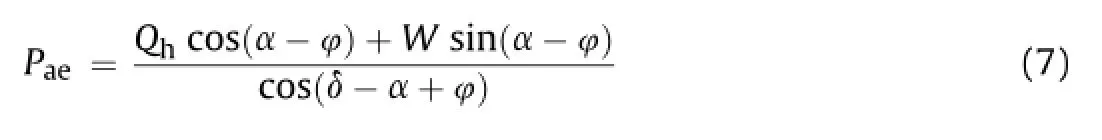
where W is the weight of the soil wedge,φ is the angle of soil shear resistance,andδis the angle of wall friction.The total lateral earth pressure coeff i cient is thus obtained as

The distribution of the total lateral pressure pae(z)is expressed as

where pad(z)and pas(z)are the dynamic and static components of the total lateral pressure,respectively.The loading point of the dynamic thrust can be expressed by

Fig.11.Normalized pressure prof i les(amax=0.3 g and f=5 Hz).(a)dw=1024,without geofoam panel;(b)dw=524,without geofoam panel;(c)dw=1024,EPS15 with ti/H=0.14; (d)dw=524,EPS15 with ti/H=0.14.

where Md(z=H)is the total bending moment at the f i xed base,and Padis the dynamic component of the total thrust.Earth pressure prof i les calculated with the analytical method and those obtained fromphysicaltests are presented in Figs.10 and 11,respectively.Thetotal earth pressures observed along the wall height are in good agreement with those calculated with the analytical procedure. However,the initial static and dynamic components were found to be signif i cantly different from those estimated by the analytical method.According to the test results presented in Fig.11,it can be inferred that the lateral arching behavior of the granular backf i ll leads to the formation of nonlinear pressure prof i les along the wall. Regarding the static and dynamic components of the total earth force,the discrepancy between the test data and the results of the analytical study could be explained with the arching effects presented in the physical model.Pressures estimated with the analytical methodology were found to be more representative for the Type-I with low f l exibility ratio,dw=128(comparison of Figs.10 and 11b).

The ratio of the dominant excitation frequency to the fundamental frequency of the wall—backf i ll system plays a major role in the magnitude of seismic pressures and wall displacements.In order to make comparisons of the seismic forces in relation to the frequency ratio achieved in the tests,the f i rst fundamental frequency(fn)of an equivalent one-dimensional linear elastic soil column can be estimated bya known height(H),shear modulus(G) and backf i ll density(ρ)as follows:

Fig.12.Location of maximum thrust in relation to(a)Acceleration amplitude,

where B is the width of the two-dimensional model.Considering the backf i ll height and the fundamental frequency of the backf i llretaining wall system for the tests carried out within this study, phase differences within the backf i ll could not be observed.However,amplif i cation of the base motion within the backf i ll could be observed for the range of investigated excitation characteristics. Since this study was performed on small-scale wall models in 1-g environment,backf i ll phasing effects were out of the scope of the investigation.

Loading points(ht/H)of the total dynamic thrust for different excitation characteristics are presented in Fig.12.According to the test data,the loading point of total thrust is estimated between 0.4H and 0.6H from the wall base.However,the loading point calculated with the analytical method is lower.This discrepancy originates from the shape of the total dynamic pressure prof i les of the physical tests and those calculated with analytical method.

6.3.Dynamic earth pressure coeff i cients(Kae)

In Figs.13—15,the lateral earth pressure coeff i cients(Kae)are depicted for wall models with different f l exibility ratios and deformable inclusion characteristics.According to Fig.13,increase of amaxcauses a nonlinear increase in Kaevalues.A good agreement can be noted between the coeff i cients calculated with the analytical method and the test data corresponding to the wall without deformable buffer.The earth pressure coeff i cients shown in Fig.13 were calculated from test data obtained from the rigid wall model Type-I(dw=128).On the other hand,wall f l exibility has a prominent role in the dynamic earth pressures as demonstrated in Fig.14.According to the test results,the total lateral dynamic forces decrease as the f l exibility ratio of the wall increases.Deformable geofoam inclusions reducing earth pressure coeff i cients depends on the inclusion characteristics and f l exural attributes of the wall. As observed in Fig.14,the inclusion with the smallest stiffness ratio(Ei/ti)provides the highest reduction.Forthewall model Type-I(dw=128),EPS15 inclusion having ti/H=0.14 providesapproximately 50%decrease in Kae.The same geofoam inclusion provides only 33%decrease in dynamic earth pressure coeff i cient for the model Type-IV(dw=8197).The inf l uence of frequency ratio（f/f*n）on Kaevalues for Type-III wall(dw=1024)is shown in Fig.15. It can be observed that Kaevalues signif i cantly increase as（f/f*n）increases.

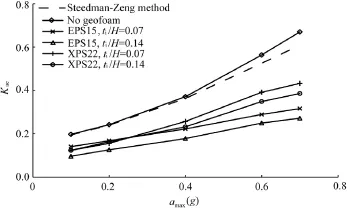
Fig.13.Variation of dynamic earth pressure coeff i cient(Kae)with amax（f/f*n=0.15）for the Type-I model(dw=128).

Fig.14.Variation of dynamic earth pressure coef fi cient(Kae)with dw(base motion

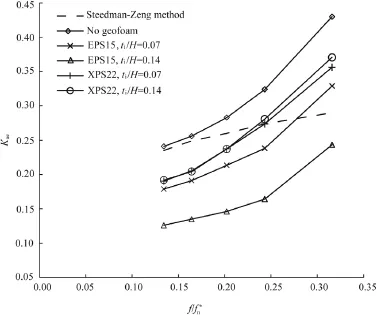
Fig.15.Variation of dynamic earth pressure coef fi cient(Kae)for wall Type-III with(amax=0.3 g,dw=1024).

7.Conclusions

In this study,results of small-scale physical tests on f l exible cantilever earth walls with deformable geofoam inclusions were presented.Wall models having different f l exibility ratios were subjected to harmonic base excitations.Deformable inclusions possessing different stiffness and thickness characteristics were installed between the model walls and the cohesionless granular backf i ll to serve as the deformable layer.Test results indicated that the wall f l exibility has a signif i cant inf l uence on the dynamic earth pressures.The dynamic earth forces and displacements of the walls with deformable panels were compared with those of the models without geofoam inclusions.Comparisons indicate that geofoam panels of low stiffness installed against the model retaining walls affect displacement and lateral pressure pro fi le along the wall height.The ef fi ciency of dynamic load and displacement reduction decreases as the fl exibility ratio of the model wall increases.On the other hand,load reduction ef fi ciency of the geofoam increases as the amplitude and frequency ratio of the seismic excitation increases.Relative fl exibility of the deformable layer(the thickness and the elastic stiffness of the polystyrene material)plays an important role in reducing seismic earth forces.Depending on the inclusion characteristics and the wall fl exibility,up to 50%reduction in dynamic lateral earth pressures may occur.According to the test results,the model retaining walls without geofoam inclusions experienced high residual stresses when subjected to the earthquakeeffectdue to densi fi cationofthe granularmaterial. Deformable inclusions reduced residual wall stresses observed at the end of seismic excitation,thus contributing to the postearthquake stability of the retaining wall.Loading point of the maximumdynamicthrustvariesbetween0.4Hand0.6H, depending on the inclusion type, fl exibility ratio of the wall and the characteristics of the harmonic motion applied to the base of the models.Dynamic earth pressure coef fi cients were compared with those calculated by the proposed analytical approach.Pressure coef fi cients calculated with this method were found to be in a good agreement with the testing results of the model walls with low fl exibility ratio.

The presented graphs concerning the earth pressure coef fi cients versus the wall fl exibility and inclusion characteristics may serve for the seismic design of full-scale retaining walls with deformable polystyrene inclusions.

Conf l ict of interest

We wish to con fi rm that there are no known con fl icts of interest associated with this publication and there has been no signi fi cant fi nancial support for this work that could have in fl uenced its outcome.

Athanasopoulos-Zekkos A,Lamote K,Athanasopoulos GA.Use of EPS geofoam compressible inclusions for reducing the earthquake effects on yielding earth retaining structures.Soil Dynamics and Earthquake Engineering 2012;41:59—71.

Athanasopoulos GA,Nikolopoulou CP,Xenaki VC.Seismic Isolation of earthretaining structures by EPS geofoam compressible inclusions—dynamic FE analyses.In:Proceedings of the 4th International Conference on Earthquake Geotechnical Engineering;2007.Thessaloniki,Greece,Paper No.1676.

Bathurst RJ,Hatami K.Seismic response analysis of a geosynthetic reinforced soil retaining wall.Geosynthetics International 1998;5(1/2):127—66.

Bathurst RJ,Zarnani S,Gaskin A.Shaking table testing of geofoam seismic buffers. Soil Dynamics and Earthquake Engineering 2007;27(4):324—32.

Duskov M.Materials research on EPS-20 and EPS-15 under representative conditions in pavement structures.Geotextiles and Geomembranes 1997;15(1—3): 147—81.

Ertugrul OL,Trandaf i r AC.Lateral earth pressures on f l exible cantilever retaining walls with deformable geofoam inclusions.Engineering Geology 2013;158:23—33.

Ertugrul OL,Trandaf i r AC.Reduction of lateral earth forces acting on rigid nonyielding retaining walls by EPS geofoam inclusions.Journal of Materials in Civil Engineering 2011;23(12):1711—8.

Hazarika H,Okuzono S,Matsuo Y.Seismic stability enhancement of rigid nonyielding retaining walls.In:Proceedings of the 13th International Offshore and Polar Engineering Conference,vol.2.Cupertino,USA:International Society of Offshore and Polar Engineers(ISOPE);2003.p.697—702.

Head KH.Manual of soil laboratory testing.Soil classif i cation and compaction tests. 2nd ed,vol.1.London:Pentech Press;1992.

Horvath JS.Geofoam geosynthetic.New York:P.C.Scarsdale;1995.

Horvath JS.Lateral pressure reduction on earth-retaining structures using geofoams:correcting some misunderstandings.In:ASCE ER2010:Earth Retention Conference 3,Bellevue,USA;2010.

Koerner RM.Designing with geosynthetics.5th ed.Upper Saddle River,USA: Prentice Hall;2005.

Matsuo O,Tsutsumi T,Yokoyama K,Saito Y.Shaking table tests and analysis of geosynthetic-reinforcedsoilretainingwalls.GeosyntheticsInternational 1998;5(1/2):97—126.

Okamoto M,Fityus SG.An evaluation of the dry pluviation preperation technique applied to silica sand samples.In:Geomechanics and Geotechnics of Particulate Media.London:Taylor and Francis Group;2006.p.33—9.

Steedman RS,Zeng X.The inf l uence of phase on the calculation of pseudo-static earth pressure on a retaining wall.Geotechnique 1990;40(1):103—12.

Trandaf i r AC,Erickson BA.Stiffness degradation and yielding of EPS geofoam under cyclic loading.Journal of Materials in Civil Engineering 2012;24(1): 119—24.

Trandaf i r AC,Ertugrul OL.Earthquake response of a gravity retaining wall with geofoam inclusion.In:Geo-frontiers 2011:Advances in Geotechnical Engineering.Reston,USA:American Society of Civil Engineers;2011.

Veletsos AS,Younan AH.Dynamic response of cantilever retaining walls.Journal of Geotechnical and Geoenvironmental Engineering 1997;123(2):161—72.

Wang MW,Iai S,Tobita T.Numerical modelling for dynamic centrifuge model test of theseismicbehaviorsofpile-supportedstructure.ChineseJournalof Geotechnical Engineering 2005;27(7):738—41(in Chinese).

Wang MW.Dynamic centrifuge tests and numerical modelling for geotechnical earthquake engineering in liquef i able soils.Beijing:Science Press;2012(in Chinese).

Wood DM.Geotechnical modeling.1st ed.New York:Spon Press;2004.

Wu G.Dynamic soil structure interaction:pile foundations and retaining structures. PhD Thesis.Vancouver:The University of British Columbia;1994.

Zarnani S,Bathurst RJ.Numerical parametric study of expanded polystyrene(EPS) geofoam seismic buffers.Canadian Geotechnical Journal 2009;46(3):318—38.

Dr.Ozgur L.Ertugrul is an assistant professor and graduate student supervisor in Department of Civil Engineering,University of Mersin.He obtained his M.S.and Ph.D.in Middle East Technical University.He earned Graduate Studies Performance Award in 2005 from Institute of Natural and Applied Sciences,Middle East Technical University.He made research on the dynamic characterization of geofoam in Department of Geology and Geophysics, University of Utah in 2009.His studies mainly concentrate on the seismic response of retaining walls,reduction of earth stresses with compressible inclusions,sesmic design of tunnels and underground structures.He has expertise on physical and numerical modeling of geotechnical problems.He has been involved in research projects funded by Turkish State Planning Organization,Middle East Technical University and Mersin University.He served as a consultant for ground improvement and deep excavations projects to the Turkish Government.He has published several papers on the seismic response of retaining walls and reduction of lateral earth stresses with deformable geofoam inclusions.He is a member of Turkish Society of Civil Engineers, Turkish National Committee of Soil Mechanics and Foundation Engineering,International Society for Soil Mechanics and Geotechnica Engineering.He makes paper reviews for journals such as Journal of Geotechnical and Geological Engineering, Lanslides and ASCE Journal of Materials in Civil Engineering.

*Corresponding author.Tel.:+90 533 393 70 66.

E-mail addresses:ozgurertugrul@hotmail.com,ertugrul@mersin.edu.tr (O.L.Ertugrul).

Peer review under responsibility of Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.

1674-7755©2014 Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.Production and hosting by Elsevier B.V.All rights reserved.

http://dx.doi.org/10.1016/j.jrmge.2014.07.004