基于模型诊断在配电网故障诊断中的应用研究

， ， ， ，，

(湖北省黄石供电公司，湖北 黄石 435000)

0 引 言

经过30多年的发展，MBD(model-based diagnosis)形成了两个有代表性的研究流派：基于一致性推理的MBD[1-3]和基于溯因推理的MBD[4-5]。基于一致性推理的MBD对诊断空间的限制较弱，它不要求任何观测被诊断逻辑推出，这就导致诊断空间中可能包含有大量的无用解；而基于溯因推理的MBD对诊断空间的限制很强，它要求所有观测需要被诊断逻辑推出，如果待诊断系统的模型不完备，则可能丢失真正解。

当配电网发生故障时，为了能够更好地辅助电网运行人员及时判断与处理故障，对配电网故障诊断来说，这就要求不仅能够指出故障元件，而且还应指出故障元件具体的故障模式，因此，如果采用基于一致性推理的MBD，那么，虽然该方法在建模方面具有比较高的效率，只需使用系统元件的正常行为模型，但这种方法所得到的候选诊断较多，诊断鉴别过程需要增加更多的观测信息，而且在最终的诊断结论中还不能指明元件所处的具体故障模式，这显然不能满足配电网故障诊断的要求；而如果采用基于溯因推理的MBD，那么，虽然该方法在理论上能够指出元件所处的具体故障模式，但这种方法由于引入了元件的故障行为模型，在建模方面存在困难，尤其是在建立完备的故障模型，而且在诊断前需要建立大量的因果理论，以蕴含配电网故障时可能表现出的各类征兆信息，否则在实际诊断过程中，由于候选诊断空间非常大，搜索蕴含故障征兆信息的诊断结论会非常耗时，甚至不能完成。

综合考虑到一致性推理MBD方法与溯因推理MBD方法所存在的不足与困难，下面将尝试将两者相结合，即混合推理的MBD方法用于配电网故障诊断。针对配电网线路的结构和故障特点，提出一种配电网线路故障诊断应用方案，以某10 kV配电网子网为诊断实例，通过对该系统进行建模、编程和实验，来验证该应用方案的可行性和有效性。

1 MBD的基本理论

为便于后面叙述与理解，先简单地介绍一下所要用到的几个基本概念[4,6]。

定义1.1 待诊断系统：一个待诊断系统是用一个三元组(SD，OBS，COMP)来表示，其中SD(system description)为系统的模型描述一阶语句，OBS(observations)为系统的观测值一阶语句，COMP(component)为组成系统的元件集合。

定义1.2 冲突集：系统(SD，OBS，COMP)的一个冲突集是一个元件集{c1，…，ck}⊆COMP，它使得SD∪OBS∪{┐AB(c1)，…，┐AB(ck)}是不可满足的。一个冲突集是最小冲突集当且仅当它的任何一个真子集都不是冲突集。其中，一元谓词AB意味着“abnormal”，AB(c1)表示元件c1异常，┐AB(c1)表示元件c1正常。

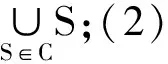
定义1.4 诊断：Δ是系统的一个诊断的充要条件，它是系统所有最小冲突集的最小碰集。系统的诊断一般通过计算系统的所有最小冲突集的最小碰集得到。

定义1.5 解析冗余关系：一种解析冗余关系是从系统模型中得出的只含有系统可观测变量的约束方程。该方程在给定任意一组观测值后能够被求值，记为r=0，其r称为残差。

定义1.6 最小冲突集候选：如果E是某解析冗余关系的最小支撑环境，则称E是一个最小冲突集候选。

将系统每个解析冗余关系所对应最小支撑环境称为一个最小冲突集候选[7]。给定一组具体的系统观测值，那些不能被系统观测值满足的解析冗余关系所对应的最小支撑环境就是系统的最小冲突集。

2 配电网诊断方案

在配电网系统中，由于配电网系统的监控设备(电流、电压互感器)的布置一般都是固定不变的，借鉴文献[8]中的方法，给出了一个将MBD理论应用于配电网故障诊断的应用方案，具体如下。①建立配电网系统、元部件的设计原理模型与故障模型；②配电网系统建模完成后，采用RGA搜索算法[9]，离线地搜索出系统中所有的解析冗余关系以及它们所关联的最小冲突集候选；③在故障发生后，利用电流、电压互感器测得的配电网故障状态信息，在线地从最小冲突集候选中搜索出最小冲突集，即将配电网的故障状态信息以及元件参数的具体值代入到解析冗余关系中，如果相对残差大于最大允许相对残差，那么这个解析冗余关系所对应的最小冲突集候选就是最小冲突集；④由所得的最小冲突集，采用逻辑数组算法[10]计算最小冲突集的最小碰集得到满足一致性推理的候选诊断；⑤利用故障模型知识，由溯因推理，对步骤(4)所得到的候选诊断进行鉴别，并给出含有具体故障描述的诊断。

3 诊断实例

图1为某10 kV配电网子网，它是具有7个节点的辐射型配电网络，其中系统等效是指除了这7个节点外的完整配电网，它的作用相当于电源，给这7个节点供电，从节点1到节点7都布置了相应的采集信息装置。该配电网子网由7条母线和6条输电线路组成。为了便于快速地找出可能的故障元件集合，图中作了两个假设：①假设母线的故障概率均为0.1；②假设输电线的故障概率都为0.4。结合第3部分提出的应用方案，采用MAPLE 12软件进行编程，对此配电网络进行仿真，以验证该应用方案的有效性和可行性。

该配电网中的设备主要包括电力变压器、输电线、母线、电压互感器、电流互感器、隔离开关、断路器以及这些设备间的连接线。为简化起见，这里考虑的故障诊断对象是母线和输电线，同时，在故障诊断过程中所使用的观测信息，以故障发生后断路器跳闸前的状态信息为基础。

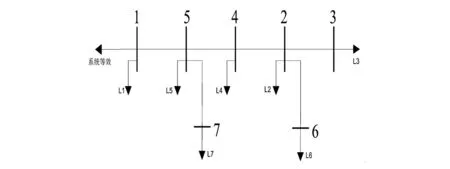
图1 某10 kV配电网子网

3.1 系统建模

3.1.1 配电网输电线的模型

该配电网系统有L15、L54、L42、L23、L57、L26等6组输电线，在正常情况下，各组输电线的每条线路的输入电流等于输出电流，且输出端电压等于输入端电压与线路中阻抗损耗之差。

1)单相输电线的统一模型

将输电线的A、B、C三相中的每一相作为一个独立的元件来建模，由于该配电网的电压等级较低，再加上输电线路较短，所以不考虑分布参数的特性，而使用集中参数模型，忽略了对地导纳，由此可得输电线的输入输出侧电压与电流的约束方程，如下。

Iin=Iout，Vout=Vin-Iout·Z·Len

其中，Iin是从输入端流入的电流；Iout是从输出端流出的电流；Vin为输入端节点电压；Vout为输出端节点电压；Z为单位长度输电线的等效阻抗；Len为输电线路的实际长度。

2)三相输电线的故障模型

本诊断实例将输电线的A、B、C三相作为一个整体进行建模，并认为三相输电线会发生各类短路故障以及断线故障，根据这些假设，得出三相输电线各内部子元件可能发生的故障情况如下。

与A相输电线有关的故障：groundA, breakA, shortInterAB, shortInterAC, shortInterABC；

与B相输电线有关的故障：groundB, breakB, shortInterAB, shortInterBC, shortInterABC；

与C相输电线有关的故障：groundC, breakC, shortInterAC, shortInterBC, shortInterABC。

表1给出了本诊断实例为三相输电线的各类故障所制定的定性故障概率值。

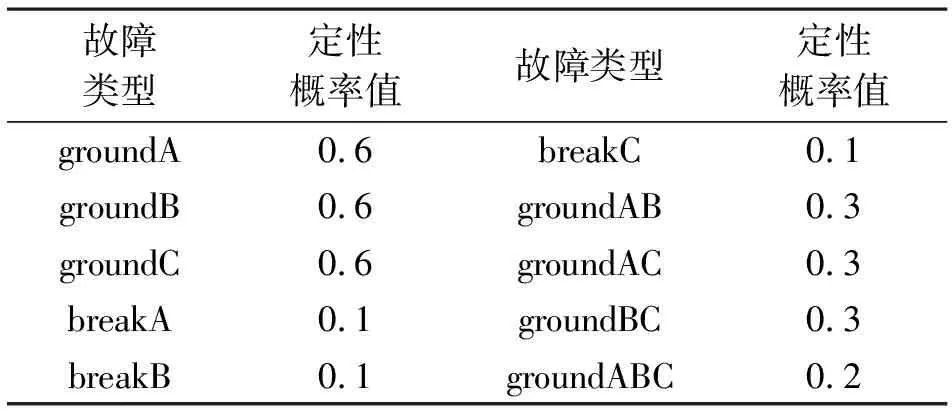
表1 三相输电线的各类故障的定性故障概率值

设_iA、_iB、_iC是三相输电线对象的各相内部子元件。现以其A相接地短路故障、A相断线故障与AB相间短路故障为例，分析三相连接线对象的故障模型。设它的内部变量如下。

IA.i、IA.o、VA.i、V：_iA输电线的输入输出端电流、电压；

IB.i、IB.o、VB.i、VB.o：_iB输电线的输入输出端电流、电压；

IC.i、IC.o、VC.i、VC.o：_iC输电线的输入输出端电流、电压。

IA.g、IB.g、IC.g：分别从_iA、_iB、_iC线路注入到地的接地短路故障电流，在接地故障时，这些值不为0，而在非接地故障时，则为0。

当输电线发生 A相短路接地故障时，相应的内部变量应该满足如下的约束关系。

IA.g=IA.i-IA.o；VA.i=VA.o= 0

当输电线发生A相断线故障时，相应的内部变量应该满足如下的约束关系。

IA.g=IA.i=IA.o=0

当输电线发生AB相间短路故障时，相应的内部变量应该满足如下的约束关系。

IA.i+IB.i=IA.o+IB.o

VA.i=VA.o=VB.i=VB.o

IA.g= 0，IB.g= 0

3.1.2 配电网母线的模型

该配电网中有7个母线，即B1，B2，…，B7，每个母线又分为A、B、C三相，因此，该配电网系统中总共有21个单相母线，由于母线具有相同的结构，因此，可以建立配电网母线的统一模型。

1)单相母线的统一模型

与输电线类似，先对单相母线进行建模。正常情况下，母线各回进出线的输入输出电流是平衡的，即两进两出的单相母线的约束方程如下。

Iin1+Iin2=Iout1+Iout2

另为每个母线对象指定一个母线电压变量Vbus。

2)三相母线的故障模型

在配电网三相母线的故障模型方面，诊断实例中，认为母线不存在断线故障问题，根据该假设，得出三相母线各内部子元件可能发生的故障情况如下。

与A相母线有关的故障：groundA, shortInterAB, shortInterAC, shortInterABC；

与B相母线有关的故障：groundB, shortInterAB, shortInterBC, shortInterABC；

与C相母线有关的故障：groundC, shortInterAC, shortInterBC, shortInterABC。

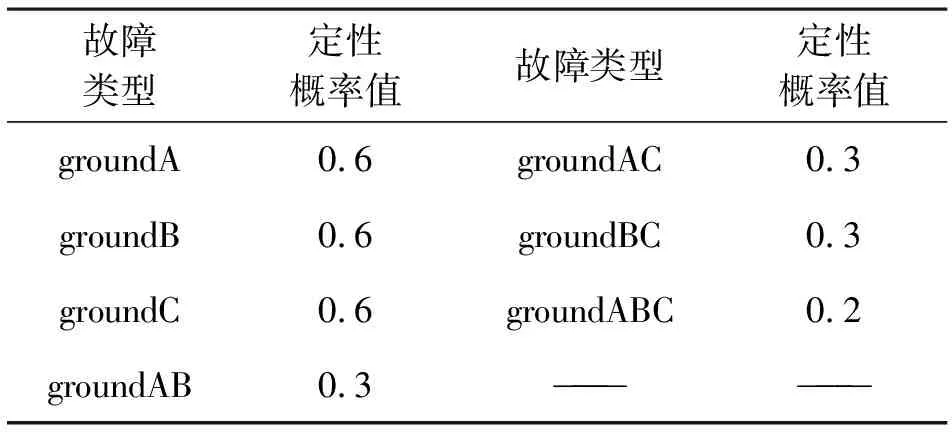
表2 三相母线的各类故障的定性故障概率值

表2给出了本诊断实例为三相母线的各类故障制定的故障概率定性值。

设_iA、_iB、_iC是三相母线对象内部的三个单相母线，现以A相母线接地故障及A相母线与B相母线的相间短路故障为例分析母线的故障模型，假设母线的内部变量如下。

Ia.i、Ia.o、Va：分别为母线_iA的各进出线连接点处的电流及母线电压变量；

Ib.i、Ib.o、Vb：分别为母线_iB的各进出线连接点处的电流及母线电压变量；

Ic.i、Ic.o、Vc：分别为母线_iC的各进出线连接点处的电流及母线电压变量；

Ia.g、Ib.g、Ic.g：分别为从母线_iA、_iB、_iC注入到地的接地短路故障电流。接地故障情况下为非0值，非接地故障时则为0。

当母线_iA发生单相接地短路故障时，与母线_iA有关的内部变量应满足约束为

Ia.g=Ia.i-Ia.o，Va= 0

当母线_iA与_iB发生相间短路故障时，与母线_iA与_iB有关的内部变量应满足约束为

Ia.g=0，Ib.g=0

Ia.i+Ib.i=Ia.o+Ib.o，Va=Vb

当母线_iA、_iB与_iC发生三相短路故障时，与三相母线有关的内部变量应满足约束为

Ia.g=0，Ib.g=0，Ic.g=0

Ia.i+Ib.i+Ic.i=Ia.o+Ib.o+Ic.o

Va=Vb，Va=Vc

3.2 诊断过程

3.2.1 最小冲突集候选

通过离线搜索得到该配电网所有的解析冗余关系及相应的最小冲突集候选共有 20个，(如：MinCSC1为最小冲突集候选，即{ B3_A，L23_A }为最小冲突集候，其对应的解析冗余关系是“0=-V3_A+V2_A-_iI_L3_A*_uZ_L23_A*_len_L23_A=0”。)，部分最小冲突集候选如下。

1) MinCSC1为{ B3_A，L23_A }；

2) MinCSC2为{ B3_B，L23_B }；

3) MinCSC3为{ B3_C，L23_C }；

……

19)MinCSC18为{ B1_A，B2_A，B3_A， B4_A, B5_A， B6_A， B7_A，L15_A， L23_A，

L26_A，L42_A，L54_A，L57_A }；

20)MinCSC44为{ B1_C， B2_C， B3_C， B4_C， B5_C， B6_C， B7_C， L15_C， L23_C， L26_C， L42_C， L54_C， L57_C }。

其中，L26_A指节点2和节点6之间的A相输电线， B1_C是指节点1的C相母线，其他的类似。

3.2.2 最小冲突集

假设在该配电网中，线路L23_A发生短路接地和线路L57_B发生短路接地故障。通过仿真获得在此故障情况下变电站内的各互感器的测量值，如表1所示，其中，V1_A为节点1母线的A相电压，_iI_L2_A为流入负荷L2的A相电流，_iI_B1_A为等效系统注入节点1母线的A相电流，其他类推。

表3 故障情况下配电网中的各互感器的测量值a)电压互感器测量值

b)电流互感器测量值

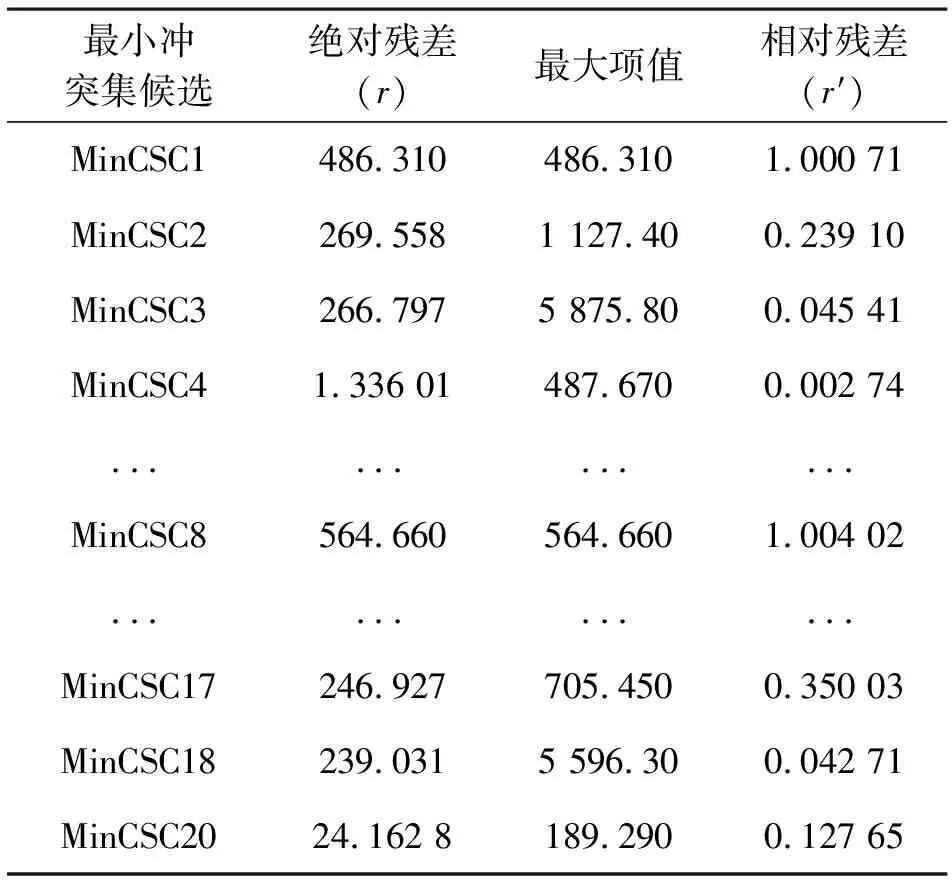
表4 解析冗余关系的残差

将上面的测量值代入到各个最小冲突集候选的解析冗余关系约束当中，所得各解析冗余关系的残差如表4所示。

由于系统模型本身存在一定的误差，使得部分解析冗余关系在正常观测下，其相对残差已超过了0.3。设允许的相对误差为0.4，从表4中相对残差r′>0.4的最小冲突集候选中得到最小冲突集。

MinCs:={{B3_A，L23_A}，{B7_B，L57_B}}

3.2.3 最小候选诊断

由冲突识别过程得到的2个最小冲突集，利用逻辑数组算法计算出它们的最小碰集，得到4个候选诊断为MinHs:={[B3_A， B7_B]，[B3_A，L57_B]，[B7_B， L23_A]，[L23_A，L57_B]}。

依据假设给定的元件故障概率定性值，采用贝叶斯定理计算上面所得的侯选诊断的故障概率，并进行故障概率排序，见表5。

表5 最小候选诊断的定性故障概率排序

3.2.4 诊断鉴别

在由溯因推理对候选诊断进行鉴别的过程中，采用优先搜索策略，即优先选择定性故障概率较大的故障模式与故障征兆信息进行匹配，如果匹配成功，则不再考虑定性故障概率更小的故障模式。

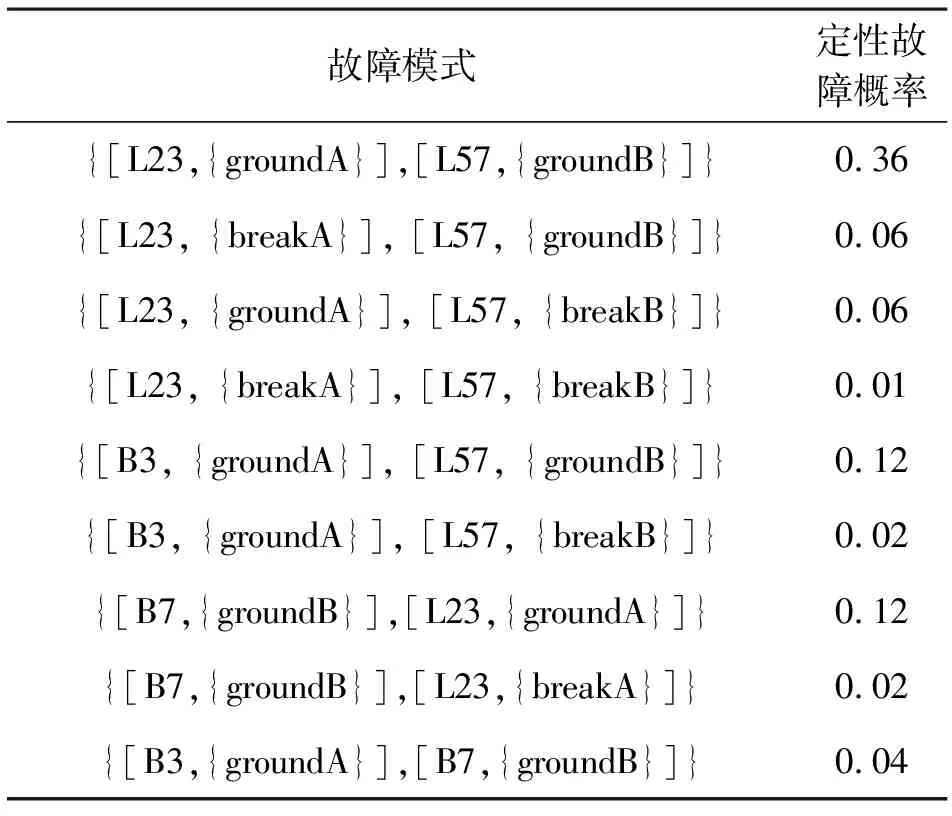
表6 各种故障模式及其定性故障概率

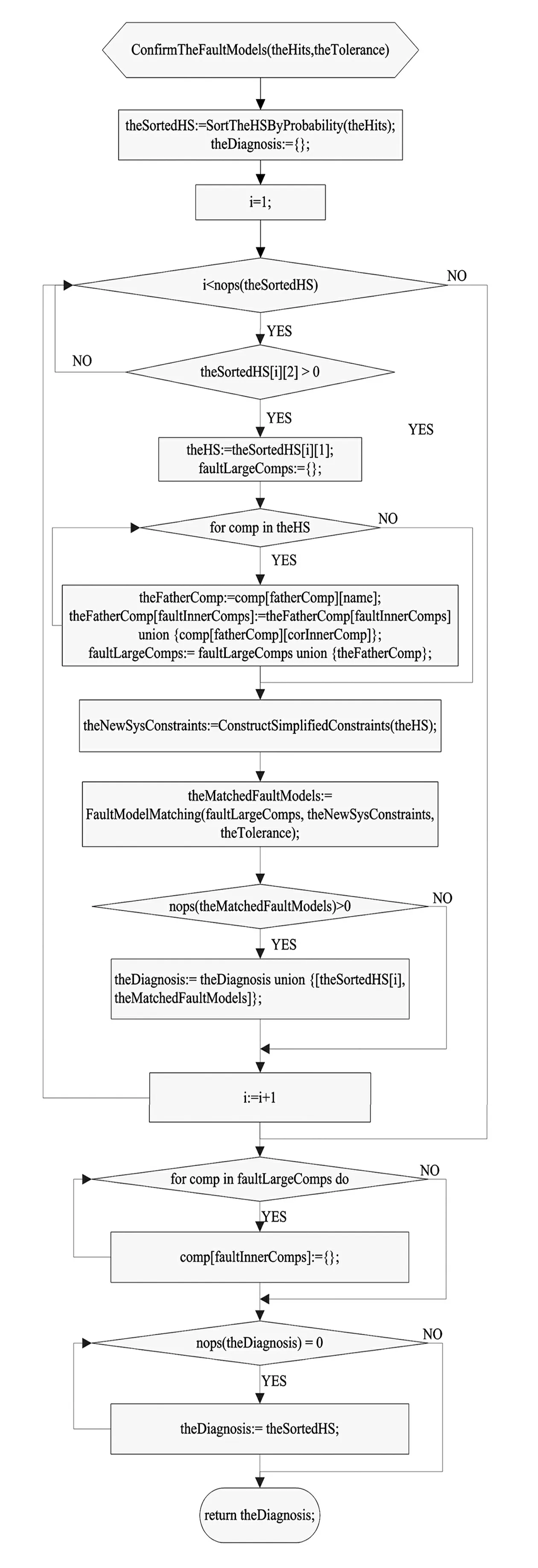
图2 故障模式匹配的程序流程图

参照表6给出的各候选诊断及其故障模式的定性故障概率的排序，选择故障模式：{ [23，{groundA}]， [L57，{groundB}]}，将该故障模式与对应的故障征兆信息进行匹配，匹配主要流程见图2，即用相应故障模式下元件故障约束代替元件的正常约束，于是，由观测信息能够得到一些新的解析冗余关系，此过程与最小冲突集识别类似，该故障模式产生出的新的解析冗余关系的最大相对残差约为0.365，由于考虑到模型本身存在一定的误差，本诊断实例在故障匹配过程中，设这些新的解析冗余关系的最大允许相对残差为0.4，经匹配(当某故障模式所对应的最大相对残差小于最大允许相对残差时，即匹配成功)，该故障模式满足条件，因此，不再考虑其他的定性故障概率较小的故障模式，即匹配过程结束，得出诊断结论，本例中的最终诊断结论如下。

{[L23，{groundA}]， [L57，{groundB}]}

由此，可判断线路L23发生A相接地故障和线路L57发生B相接地故障，此结论正好与前面的假设相符。

4 结 论

传统的配电网故障诊断是在故障后根据保护和断路器动作信息来判断故障场景，而所采用的MBD方法，可以直接利用量测量来判断最有可能发生故障的元件，即根据故障发生后保护动作前的量测量识别出可能的故障元件，具有较好的预警性。从诊断实例中可以看出，采用混合推理的MBD方法，在获得候选诊断过程中使用一致性推理方法，并针对配电网内监测点位置的不变性将最小冲突集的搜索问题分为离散搜索最小冲突集候选与在线识别最小冲突集两个步骤，而在候选诊断过程中采用溯因推理的方法，使用了配电网内设备的常见故障模型知识。从最后的诊断结果来看，这种混合推理的MBD方法能够在不增加额外观测信息的情况下给出正确的诊断。

前面将MBD方法用于配电网线路故障诊断，虽然取得了不错的效果，但由于配电网本身的复杂和庞大，在配电网的建模方面(元件建模、系统建模、系统结构改变建模等)、量测量处理(相位、时间、约束条件、不确定性)等诸多方面存在问题；而且，MBD方法本身在最小冲突集与碰集搜索算法、推理算法和约束关系等方面仍存在进一步改进的可能。

[1] Genesereth M R. The Use of Design Descriptions in Automated Diagnosis[J]. AI, 1984, 24 (1-3): 411-436.

[2] Davis R. Diagnostic Reasoning Based on Structure and Behavior[J]. Artificial Intelligence, 1984, 24(1-3): 347-410.

[3] de Kleer J. Local Methods for Localizing Faults in Electronic Circuits[R]. Boston, USA: MIT Artificial Intelligence Laboratory, 1976.

[4] Reiter R. A theory of Diagnosis From First Principles[J]. Artificial Intelligence, 1987, 32(1): 57-95.

[5] Poole D, Goebel R, A Leliunas R. Theorist: A Logical Reasoning System for Defaults and Diagnosis[C]. In:Cercone M, Calla G M C, eds. The Knowledge Frontier. New York: Springer Verlag, 1987. 331-352.

[6] De Kleer J, Mackworth A K, R Reiter. Characterizing Diagnoses and Systems[J]. Artificial Intelligence, 1992,56 (2-3):197-222.

[7] Cordier M O, Dague P, Dumas M, et al. A Comparative Analysis of AI and Control Theory Approaches to Model-based diagnosis[C].14th European Conference on Artificial Intelligence, 2000: 136-140.

[8] Cordier M O, Dague P. Conflicts Versus Analytical Redundancy Relations: A Comparative Analysis of the Model Based Diagnosis Approach From the Artificial Intelligence and Automatic Control Perspectives[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B, 2004, 34(5).

[9] 刘志刚, 钟炜, 邓云川，等.牵引变电站故障的基于模型诊断方[J]. 中国电机工程学报, 2010,30(34):36-41.

[10] 林笠. 基于模型诊断中的用逻辑数组计算最小碰集[J]. 暨南大学学报,2002,23(1):24-27.