条件期望在微分博弈中的应用

朱庆峰， 张 慧， 邓 伟

(1.山东财经大学数学与数量经济学院, 山东 济南 250014；2. 山东建筑大学 理学院, 山东 济南 250101)

条件数学期望[1]是现代概率论中最重要的概念之一.众所周知，鞅，Markov过程[2]等一些现代概率论最基本对象就是用条件期望定义的.条件期望对初学者也是一个难点，特别是对概念的理解和对这一数学工具的使用初学者较难掌握.为了让本科学生比较深刻地学习有关理论以及认识到该知识点的广泛应用，本文介绍了条件数学期望的定义与性质，并以条件数学期望为工具，研究了一类部分信息下线性二次非零和平均场微分博弈问题[3]，并通过关于部分信息取条件数学期望，得到了该博弈问题的纳什均衡点.

1 条件数学期望的定义及性质

给定概率空间 (Ω,F,P)，T>0是固定的时间常数，信息流{Ft}0≤t≤T是由1维标准布朗运动{Bt}0≤t≤T生成的σ-域，即Ft=σ{Bs;0≤s≤t}，且满足通常的假设，令F=FT.

定义1[4]设{Ai}1≤i≤m是Ω的一个有限划分，且Ai∈F,P{Ai}>0,1≤i≤m,令G是由{Ai}1≤i≤m生成的σ-代数.对一可积随机变量X，令

称E[X|G]为X关于G的条件数学期望.

性质1[4]条件数学期望有如下基本性质：

(1)E[E[X|G]]=E[X];

(2)若X为G可测，则E[X|G]=X；

(3)设a,b为实数，X,Y,aX+bY的期望存在，则E[aX+bY|G]=aE[X|G]+bE[Y|G];

(4)设X及XY的期望存在，且Y为G可测，则E[XY|G]=YE[X|G].

2 条件数学期望在微分博弈中的应用

研究部分信息平均场倒向线性二次非零和微分对策问题.考虑如下平均场博弈系统

(1)

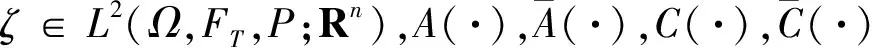
Ji(v1(·)，v2(·))=

Ni(t)(yv1,v2(t))2+

i=1,2,

(2)

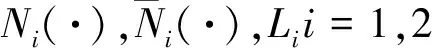
部分信息下微分博弈问题就是寻找纳什均衡点(u1(·)，u2(·))∈Rk×Rk,使得

(3)

为了证明均衡点的存在性引入下列假设

(H)Bi(Mi)-1(Bi)TΞT=ΞTBi(Mi)-1(Bi)T,

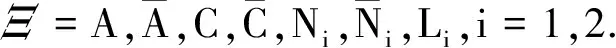
通过取关于部分信息Et的条件数学期望，给出纳什均衡点的表达式.

定理1 函数

(u1(t),u2(t))=

(4)

是上述博弈问题的一个纳什均衡点，其中(p1(t),p2(t),y(t),z(t)是下列方程的解:

(5)

证明利用条件数学期望的定义和性质，下面给出上述表达式的合理性.取关于Et的条件期望

(6)

并且函数(u1(·),u2(·))可改写为

(u1(t),u2(t))=

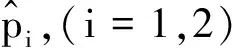
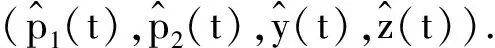
3 结束语

本文以条件期望的形式给出了一类部分信息下线性二次非零和平均场微分博弈问题均衡点的显式表达式．并根据条件期望的定义和性质，证明了该显式表达式的合理性．希望通过采用理论与经济模型相结合的教学方法，增加学生的课外实践机会、自学机会和创新机会，调动学生学习的主动性和积极性，使学生把学到的理论知识应用于解决实际问题．

[1] 茆诗松，濮晓龙，程依明. 概率论与数理统计教程[M]. 北京：高等教育出版社，2011.

[2] 张波，商豪.应用随机过程[M].北京：中国人民大学出版社，2014.

[3] 严加安.测度论讲义[M].北京：科学出版社，1998.

[4] Issacs R. Differential games[M]. New York: John Wiley and Sons, 1965.

[5] Min H, Peng Y, Qin Y.Fully coupled mean-field forward-backward stochastic differential equations and stochastic maximum principle[EB/OL].(2014-04-13)[2014-06-12]http://www.hindawi.com/journals/aaa/2014/839467.