基于时间效应的广义信度模型

刘志海, 张 强

(1.哈密市商业银行股份有限公司， 新疆 哈密 839000；2.石河子大学 理学院， 新疆 石河子 832000)

在非寿险精算中,信度理论来对未来时期经验保费的厘定具有重要的意义.主要是通过结合投保人个人的索赔经历与先验保费来共同决定保费，所制定的保费为两者的加权和.关于信度理论的详细介绍，可见文献[1].为了计算各种情况下的信度保费，人们建立了各种各样的信度模型，多数假设历史时期的索赔具有共同的风险参数,在风险参数给定下,各期的索赔满足独立同分布的的条件.然而,在保险实务中，这种假设有时候是不成立的，风险参数对时间存在着依赖性.近年来，关于风险之间的相依性的研究受到越来越多的精算研究者的关注.文献[2]在提出一种共同效应随机变量的前提下，建立了风险间有某种相依结构的信度模型，文献[3]提出了共同效应相依的信度模型，推广了文献[2]的结果. 此外，文献[4]在风险不是独立的条件下，得到了风险等相关的多合同模型的估计.文献[5]考虑了给定风险参数历史索赔服从不同分布的情形，得到了风险间等相关下的广义信度估计.文献[6]在假设误差呈现等相关正态—正态分布下得到了Bayes保费，建立了误差等相关的Bühlmann信度模型，从而推广到Bühlmann-Straub信度情形.文献[7]研究了不同年风险间的时间效应，在平方损失函数下给出了具有时间变化效应的信度模型.

另一方面，保险公司制定下一年保费的时候，往往希望与某个目标(如上一年的保费等)相差较小.平衡损失函数得到了广泛的应用，文献[8]在平衡损失函数下讨论了广义的信度模型.文献[9]在平衡损失函数下给出了Bühlmann-Straub模型的信度估计，并讨论了性质.文献[10]在平衡损失函数下给出了风险具有共同效应的信度估计，推广了文献[9]的结果.文献[11]在平衡损失函数下研究了风险相依回归的信度模型，同时得到了风险等相关与共同效应的回归信度估计.

本文考虑了不同年份的风险有时间效应，采用某种相关矩阵来刻画时间变化效应，在平衡损失函数下讨论了具有时间变化效应的信度估计.

1 模型假设与准备知识

本文研究满足如下假设的风险间具有时间变化效应的信度模型.

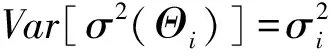
假设3平衡损失函数为如下形式

L(A,B)=w(δO(X)-A-BX)2+

(1-w)(Xn+1-A-BX)2

(1)

其中δO(X)为Xn+1的已知目标估计

在上述的假定下，我们的目标是基于所有的历史索赔数据X=(X1,X2,…Xn)′，来估测未来年的索赔Xn+1的保费，此时需要解决最小化问题

(2)

μδ=E[δ0(X)],Cov(δ0(X),Xi)=d,

d=(d1,d2,…,dn)

下面陈述一些准备型的引理.

引理1在假设1，假设2下，有以下结论

(1)Xi的均值E(Xi)=γiμ,i=1,2,…,n

(2)X可表示为X=(X1,X2,…,Xn)′,

Cov(Xn+1,X)=τn+1(τ1,τ2,…,τn)

详细证明可参见文献[3].

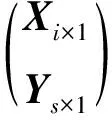
其中∑YX是Y与X的协方差矩阵，证明可见文献[12].

由引理2可知，随机变量Y在随机向量X的非齐次函数类L(X,1)上的正交投影为非齐次信度估计，即有

(3)

2 平衡损失函数下的信度保费估计

定理1在假设1和2下，通过求解最小化问题，可得未来索赔Xn+1的非齐次信度估计为

其中：

证明令Y=IδO(X)+(1-I)Xn+1,随机变量I满足P(I=1)=1-P(I=0)=w.

此时最小化问题转化为

(4)

应用引理2，可得Xn+1的信度估计为

(5)

由Y的定义，E(Y)可表示为

E(Y)=wμδ+(1-w)μ

(6)

事实上有E(Y|I)=E(X),从而可知

Cov(E(Y|I),E(X|I))=0

协方差矩阵∑YX为

∑YX=Cov(Y,X)=wCov(δ0(X),X)+

(1-w)Cov(Xn+1,X)=

wd+(1-w)τn+1(τ1,τ2,…,τn)

通过引理1，有

(7)

和

(8)

结合(5)-(8)式，可得Xn+1的信度估计为

3 结束语

信度理论作为非寿险精算学的核心内容之一，已成为非寿险保险公司精算部门重要的工具.由于现实复杂，一般情况下，风险之间都存在着某种相依性.本文考虑历年风险具有时间效应，在平衡损失函数下得到了风险具有时间变化效应的信度保费，所得到的信度估计依然为经典信度模型的加权形式，这一结果推广了经典的信度模型，可为非寿险保险公司制定下期保费提供理论依据.

[1] 温利民,林霞,王静龙. 平衡损失函数下的信度模型[J].应用概率统计,2009,25(5):553-560.

[2] 张强,崔倩倩,张娟.一类基于风险等相关的广义信度保费[J].山东理工大学：自然科学版,2012,26(6):98-102.

[3] 郑丹,章溢,温利民.具有时间变化效应的信度模型[J].江西师范大学学报：自然科学版,2012,36(3):249-252.

[4] Bühlmann H, Gisler A. A course in credibility theory and its application[M].Netherlands: Springer, 2005.

[5] Yeo K L, Valdez E, Valdez E. A Claim Dependence with Common Effects in Credibility Models[J].Insurance: Mathematics and Economics, 2006, 38(3):609-629.

[6] Wen L M, Wu X Y, Zhou X. The credibility premiums for models with dependence induced by common effects[J]. Insurance: Mathematics and Economics, 2009, 44(1):19-25.

[7] Wen L M. The credibility models with equal correlation risks[J]. Journal of Systems Science and Complexity, 2011,24(3):532-539.

[8] Wen L M，Wang W，Yu X L．Credibility models with error uniform dependence[J]．Journal of East China Normal University:Natural Science,2009,9(5)：119-126．

[9] Gomez-Deniz E. A Generalization of the credibility theory obtained by using the weighted balanced loss function[J]. Insurance: Mathematical and Economics, 2008, 42(2):850-854.

[10] Hwang W Z, Wu X Y. The credibility premiums with common effects obtained under balanced loss functions[J]. Chinese Journal of Applied Probability and Statistics,2012,28(2):203-216.

[11] Hwang W Z. Regression credibility model with correlation risk under balanced loss function[J]. Journal of East China Normal University :Natural Science, 2013(1):30-40.

[12] Radhakrishna R C, Toutenburg H,Shalabh H C,etal.Linear models and generalizations:least squares and alternatives[M].New York:Springer,1995.