低温环境下混凝土损伤模型初探

李鹏飞 秦丹丹

1 空军勤务学院机场共参与保障系（221000） 2 南京住房发展中心南京办事处（221000）

低温环境下混凝土损伤模型初探

李鹏飞1秦丹丹2

1 空军勤务学院机场共参与保障系（221000） 2 南京住房发展中心南京办事处（221000）

由损伤的定义可知，损伤的发展取决于微缺陷（微裂纹、微孔洞）的演化发展，因此，可将有损的钢纤维混凝土材料简化为一个微缺陷随机分布在基体当中的模型，再对低温环境下混凝土损伤进行研究。

低温；损伤模型；实验模拟

1 混凝土低温环境下损伤模型探讨

图1所示为钢纤维混凝土应力—应变曲线，因此可对该模型作如下假设：

图1 -40℃钢纤维混凝土应力—应变曲线

1）材料基体的弹性模量恒为E，其由无损材料的晶体结构决定，只要不发生相变，其就为恒值。

2）材料未损伤区的承载能力满足胡克定律，其真实的应力应变曲线为线性关系；材料损伤区也能承受应力，其承载能力由损伤值D决定，其关系式为σ=K（D）。当σ＜K（D0）时，微缺陷不发生变化，损伤不发展。式中D0为初始损伤，若材料的初始状态为无损状态，则D0=0。

3）材料整体的承载能力由损伤区决定，当损伤D发展到一定程度时，材料破坏，此时其残余强度σZ＞0。未损伤区依旧发生弹性卸载。

对于钢纤维混凝土,可认为其为各向同性材料，相应地，假设该材料中的损伤也是各向同性的。取一个典型的材料单元如图2所示，则有典型单元基体所产生的弹性应变εe，典型单元内所有微缺陷所产生的应变为εc,假设基体内共有N个微缺陷,每个缺陷所产生的应变为′,则微缺陷产生的总应变εc和每个缺陷产生的应变′对应的有如下关系式：

相应地，典型单元的总应变ε与基体弹性应变εe和所有微缺陷所产生的应变εc有如下关系：

对于有损材料，其应力应变关系可表示为如下形式：

式中D为材料的损失因子，E为材料的体积弹性模型。根据经典弹塑性力学理论，应力应变有如下关系式：

对比2和3可将损伤因子定义为：

如图2所示。

图2 试件单元示意图

若将材料的初始总体积定为V0,损伤演化发展后的体积为V，微缺陷的初始体积为Vd0，损伤演化发展后的体积为Vd，则有：

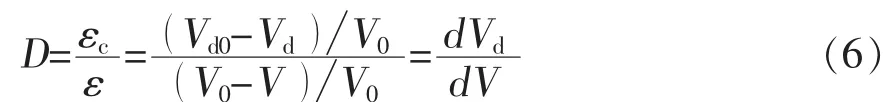
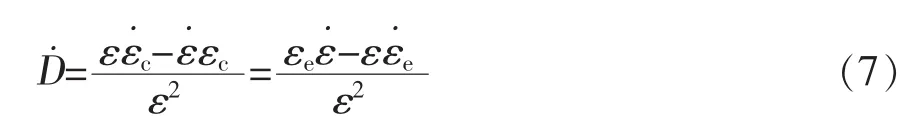
上式表明，损伤因子D实际上是微孔隙率的动态变化率。对式6求导得：对于弹性阶段而言,有ε=εe,此时亦有，代入上式可知此时，故在弹性阶段，损伤D不发展。为简化计算，这里取材料的初始损伤D0=0。

2 低温混凝土损伤模型唯象的物理解释

相比较于Lemaitre的等效应变假设而言，本模型可以说是基于等效应力假设[7]。就该模型而言，可解释为如下的唯象物理简化模型，该模型是一个弹簧B和一个单向运动物体A的串联体,如图3所示。

在该模型中，P表示一个单向运动的活塞杆，其所能承受的应力σ=K（Dp）,当载荷应力σ＜K（Dp）时，P不运动，此时损伤恒为Dp，弹簧B发生弹性变形，即材料的应力应变关系表现为线性；当荷载提供的应力σ＞K（Dp），P便开始向左运动，P向左的运动距离εc不断增加，此时的总应变ε为P的运动距离εc和弹簧B产生的弹性应变εe之和，即ε=εe+εc，故应力应变曲线表现为非线性；卸载时，弹性应变εe逐渐恢复，但P却不能向右运动以恢复变形，即材料的卸载应力应变关系表现为线性。当P不断向左运动时,P的运动距离εc不断增大,即损伤D在不断上升,当其达到某一定值DZ时，材料发生破坏，但此时的应力σZ并不为0，即σZ=K（DZ），σZ称为残余强度，材料表现出脆性特征。

图3 低温混凝土损伤模型的物理简化模型

3 损伤模型的实验模拟

在一维情形下，微缺陷演化发展所产生的应变εc与经典弹塑性理论中的塑性应变εP相等，故损伤因子D可表示为：

单轴加载条件下钢纤维混凝土的损伤模拟采用SHPB试验数据，由上式得到的损伤如图3、4、5、6所示。图中虚线部分为模拟曲线。

图4 -40℃下0%钢纤维试件损伤与应变关系曲线

图5 -40℃下1.0%钢纤维试件损伤与应变关系曲线

图7 -40℃下2.0%钢纤维含量损伤与应变曲线

由图可以清楚看出：随着钢纤维体积量的不断增加，试件的损伤值逐渐变小，其开始发生损伤时对应的应变也不断增大，体现了钢纤维对试件的增强、增韧作用，能够减少混凝土构件的损伤。

观察D-ε曲线,发现损伤因子D与ε成指数关系，故可用下式模拟损伤因子D与ε的关系：

式中K为与材料相关的常数，其值见表1。

图中模拟曲线（虚线部分）为使用Origin软件模拟而成，从模拟曲线图上可以看出，该模拟与试验数据具有较好的相关性。

表1 模拟参数表

由于试验数据偏少，上表中的K值并不是十分精确，但不难看出，随钢纤维体积率的提高，K值有明显的减小趋势。

以上均是模拟温度为-40℃时，不同纤维含量的钢纤维混凝土试件的损伤因子与应变的关系曲线,此时应变率为104.72 s-1,K值的确定也是基于这一基础。因此，为了验证K值是否在其他应变率下仍具有意义，特别对-40℃下应变率为44.50 s-1和95.12 s-1时采用此模型进行验证，其D-ε曲线如图8所示。

1）从图中可以看出，K值的选择具有一定的推广意义,虽然是在应变率为104.72 s-1的情况下推导出来的,但是在其他应变率下也有一定的使用价值。

2）从图中可以明显看出，随着纤维体积含量的增加，其损伤起始应变有所增大，这也反映了钢纤维对混凝土的增强阻裂作用，与实际试验情况相吻合；同时可以发现，当钢纤维含量增大时，高纤维含量试件的损伤D要小于同应变率下的低纤维含量试件，这也在一定程度上说明了随着钢纤维含量的增加，混凝土在冲击荷载作用下所受的损伤有所减少。

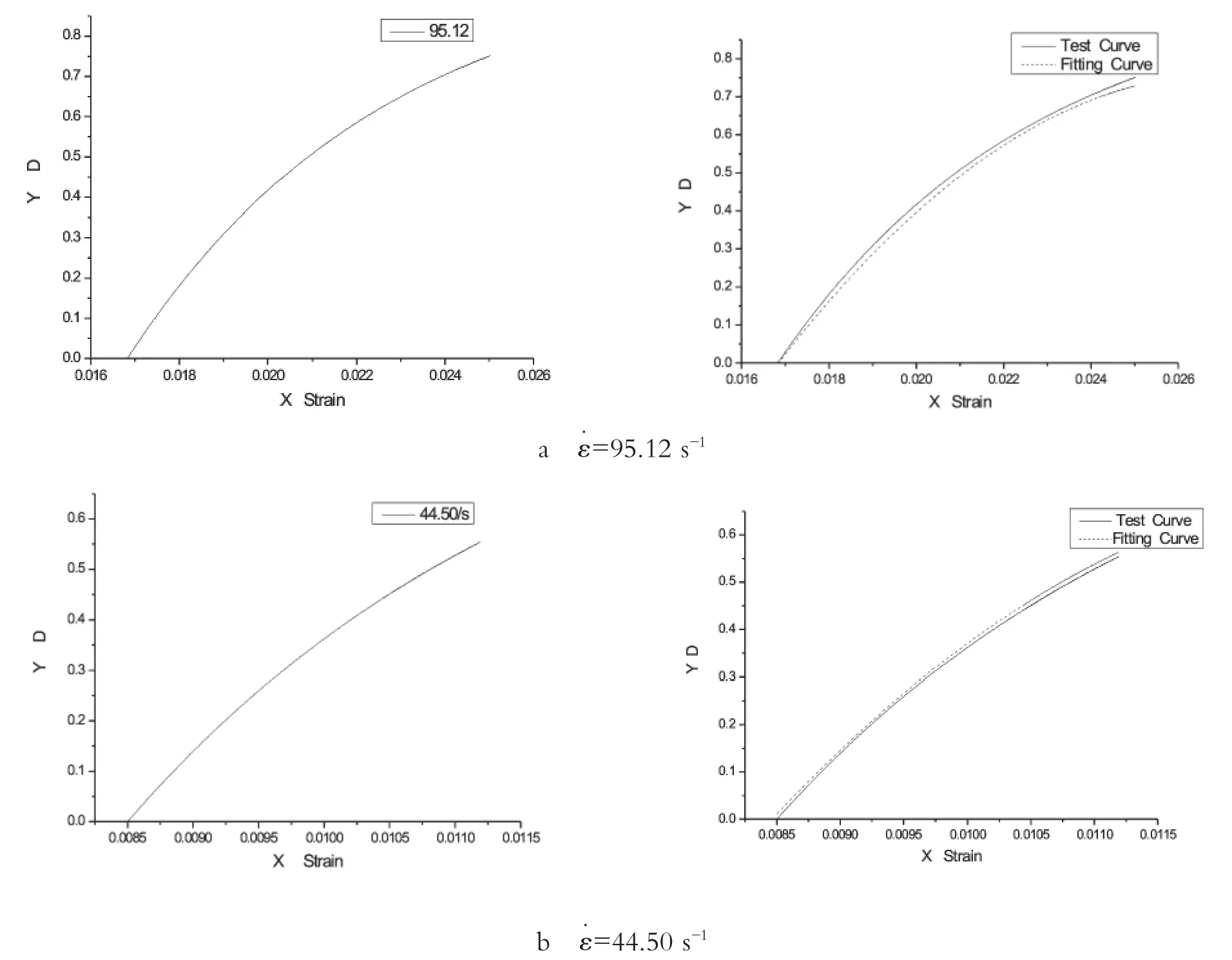
图8 -40℃下钢纤维试件损伤与应变曲线图

[1]谢剑,王传星,李会杰.超低温混凝土降温回温曲线的试验研究[J].低温建筑技术,2010,3：1～3.

[2]姚武.聚丙烯腈纤维混凝土低温性能的研究[J].建筑材料学报,2003,(6)3：243～247.

[3]吴宏阳.受冻条件下混凝土温度应力的研究[J].工程技术：96～97.

[4]张立.钢纤维混凝土低温力学性能试验研究[J].淮南师范学院学报,2009,11(3)：9～10.

[5]武鹤,魏建军,高伟.低温冰冻条件下聚丙烯纤维网混凝土疲劳性能试验研究[J].黑龙江工程学院学报,2008,22(4)：4～11.