粘滞系数测定误差分析

乔庆军，张 涛

（南阳医学高等专科学校，河南 南阳 473000）

粘滞系数测定误差分析

乔庆军，张 涛

（南阳医学高等专科学校，河南 南阳 473000）

用奥氏粘度计测量液体粘度是常用的粘度测量方法之一，但是经常存在较大误差。本文分析该实验中的系统误差和可能的偶然误差，提出减小误差的方法。

粘滞系数；奥氏粘度计；误差

当液体内各部分之间有相对运动时，接触面之间存在内摩擦力，阻碍液体的相对运动，这种性质称为液体的粘滞性，液体的内摩擦力称为粘滞力。粘滞力的大小与接触面面积以及接触面处的速度梯度成正比，比例系数η称为粘度（或粘滞系数）。

奥氏粘度计（Ostwald-viscosimeter）用于测量液体粘度，在临床上及医药行业被广泛使用。比如测定血液的粘度，对了解血液的流动性及其在生理和病理条件下的变化规律，评价微循环障碍的原因以及诊断和防治血液粘度异常疾病具有重要意义。本文给出了奥氏粘度计测量的原理，并分析了实验误差的原因。

1 问题的提出

用奥氏粘度计测量粘度是利用已知液体的粘度来测量、求得待测液体的粘度，所以是一种间接比较法。

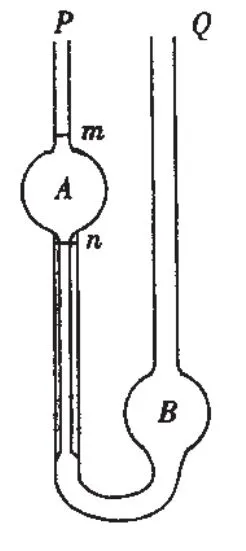
图1 奥氏粘度计

以酒精粘度测量为例：让一定体积（V）的液体（水或酒精）在重力作用下于粘度计的左侧从上向下流动，液柱高度为h，液柱长度为L，管半径为r，促使液体流动的液柱的上下表面压强差为△p，液体流量为Q，液面从m下降到n（如图1）所用的时间为t，液体的粘滞系数为η。由泊肃叶公式：Q=πr4△p/8ηL，其中Q=V/t，△p=ρgh，

故泊肃叶公式变为 V/t=πr4ρgh/8ηL

若将蒸馏水（标准液体）流动的数据代入上式，得到：

V/t水=πr4ρ水gh水/8η水L水

将待测液体（酒精）流动的数据代入上式，得到：

V/t酒=πr4ρ酒gh酒/8η酒L酒

如果两次的液体体积相等，且液柱都是竖直状态，则h水= h酒，L水=L酒

两个等式相除，得到：

η酒=ρ酒t酒η水/ρ水t水

所以只要知道水的粘滞系数、水和酒精的密度，测出同体积的水和酒精分别从m流动到n所用的时间t水和t酒，就可以算出酒精的粘滞系数。

实验步骤是：

（1）将粘度计用夹子K固定，放入盛水的水槽中并使之竖直；

（2）用注射器或量筒将5 ml的蒸馏水自B管注入，然后用橡皮球从A泡开口处向上吸管中的液体，直至液面超过刻痕m，注意不可使液体吸入橡皮球内；

（3）松开橡皮球，使液面下降，当液面经过m时开动秒表，液面继续下降，当它通过n时将秒表停住；

（4）重复上述步骤（2）、（3），共做3～5次，并求出平均值t水；

（5）将蒸馏水倒出，用酒精洗净粘度计后，将5 ml纯酒精注入粘度计，重复上述步骤（2）、（3），共做3～5次，并求出平均值t酒；

（6）利用公式η酒=ρ酒t酒η水/ρ水t水计算。

用奥氏粘度计测量粘度是常用的粘度测量方法之一，但是在实验时测量结果往往有较大的误差。产生误差的原因很多，有偶然误差，也有系统误差。关于误差的来源，现分析如下。

2 系统误差来源分析

（1）本实验最后计算酒精粘滞系数的公式η酒=ρ酒t酒η水/ ρ水t水中的两个t是测量得出的，其他3个量ρ酒、ρ水和η水是通过查表得出的已知数，不少教材的实验中提供的表格中，温度每相差5℃给一个数值，所以应用时只能取相近温度下的数值作为已知数代入公式计算，自然得出的结果不准确。

全国卫生类高职高专规划教材《物理》[1]中所给出的数据见表1。

在医生诊断完毕之后，都会开列出医嘱，在此过程中需要有两名医生和护士来共同核对药物数量，在药物使用过程中还需要严格的执行药物的“七对、三查、一注意”制度，能够明确出药物是否得到了正确的使用，对患者进一步加强负责。

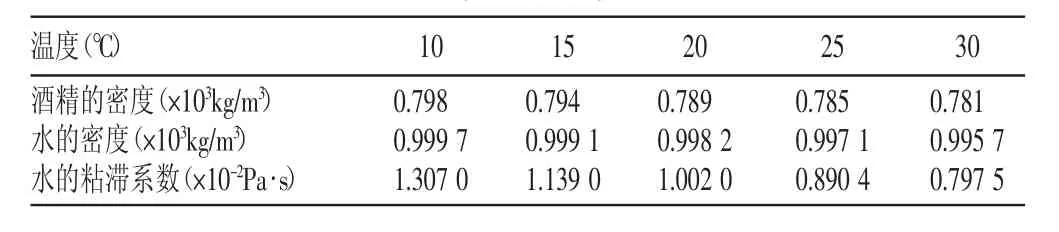
表1 实验所需资料表

若改为更精确的数据，见表2～4。

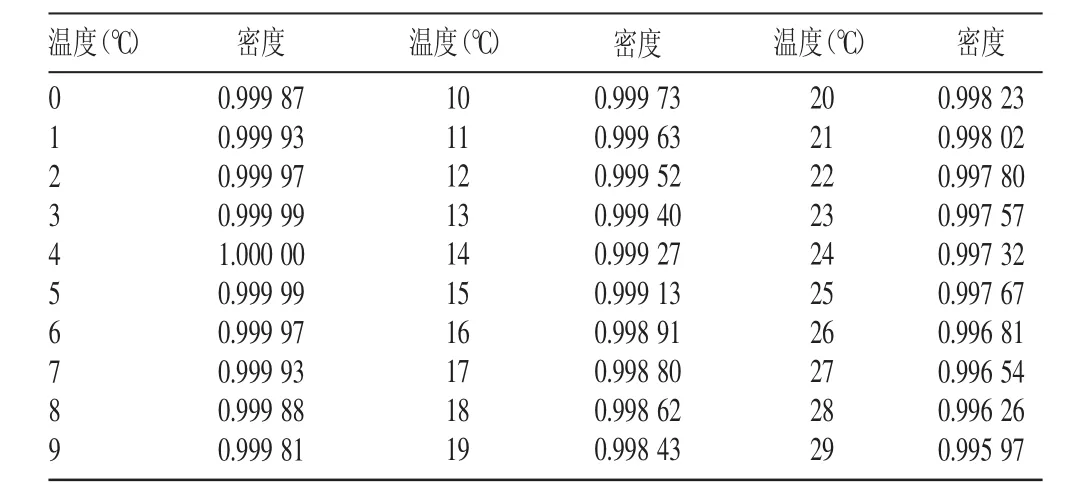
表2 水的密度（×103kg/m3）

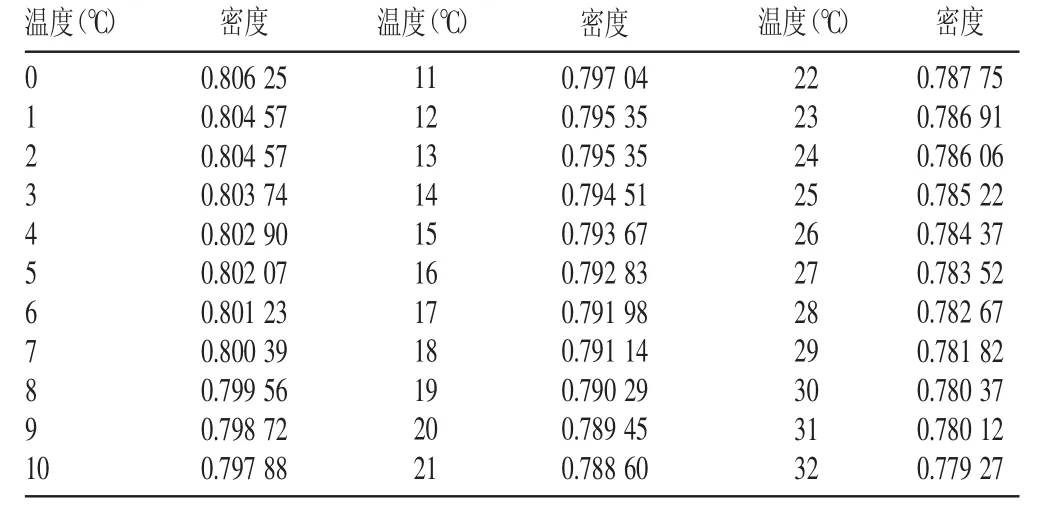
表3 酒精的密度（×103kg/m3）

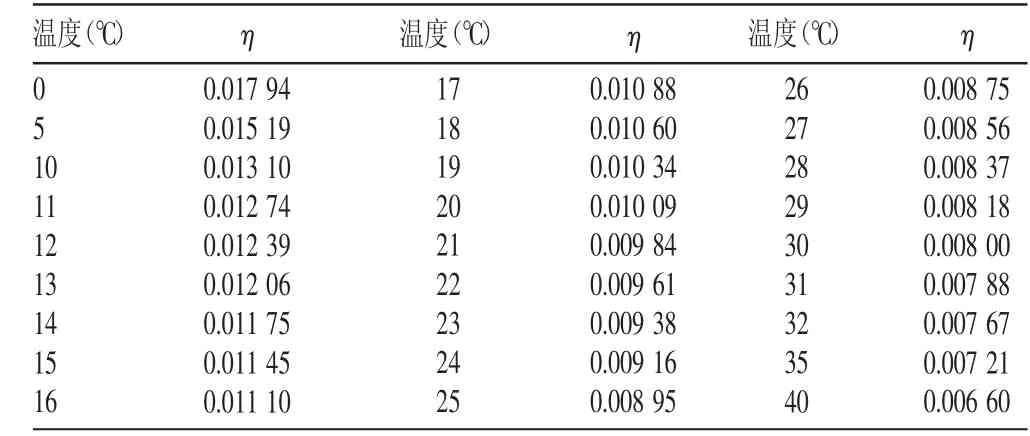
表4 水的粘滞系数（Pa·s）

代入公式的已知数越精确，最终的计算结果自然会越准确。

（2）由时间测量引起的误差。实验中，需用秒表测量水和酒精从管子中下降所用的时间。秒表在使用时要有反应时间。开始时，一般可以实现松开洗耳球与开始计时同步，但计时终点通常要有一个反应时间，这使得代入公式的时间数值偏大。

由η酒=ρ酒t酒η水/ρ水t水=ρ酒η水/ρ水×t酒t水而，所以最终计算得出的数值η酒偏小。

3 偶然误差来源分析

3.1 由液体体积引起的误差

实验中两次测量时，是用移液管分别取相同体积的水和酒精，这个体积，正常情况下应该是6 ml，且两次测量中的水和酒精体积要相同。

（1）水量与酒精量不同：

如果水的体积大，酒精体积小，则水从管子中流下所用的时间t水变大，根据公式η酒=ρ酒t酒η水/ρ水t水，

计算得出的酒精粘滞系数η酒会偏小。

（2）两次测量时，用移液管取的水和酒精量虽然相同，但是体积都过少：则在把液体注入B泡时，不能充满，用洗耳球吸到另一侧的A球时，液体也不能充满A球，而实验者就以这里（而不是刻度“m”）为起点开始计时，测量得出的时间就不是实验所要求的“液面从m下降到n所用的时间”。

而且由于液面不能充满整个A球，导致用洗耳球吸的时候，液体最多只能上升到图中所示位置，再吸，液体就会像沸腾了一样，冒出大量气泡（如图2），也就会有液体溅到A球上边的玻璃管口，溅到玻璃管口的液体被洗耳球吸走，就不能保证两次实验的液体体积相同。

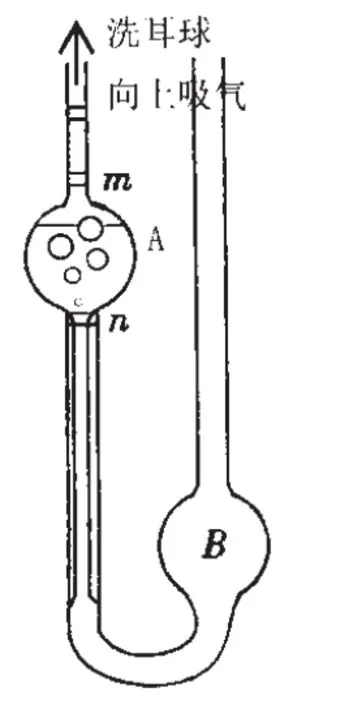
图2 液体量过少时的情况

所以，实验中，用移液管取水和酒精时，都要取6 ml，两次相等，保证最初能充满B球；用洗耳球吸到另外一侧以后，能充满A球。

3.2 由酒精浓度引起的误差

实验要测量的是纯酒精的粘滞系数，而学生实验每次用的酒精是回收利用的，所以经常测出的粘滞系数既不是98%酒精的，也不是75%酒精的，总之是加水酒精的粘滞系数，比纯酒精的粘滞系数偏小。

3.3 由温度测量引起的误差

实验要求水和酒精的温度相同，实验要在大烧杯的热水中进行，但是，由于实验者在空气中进行实验，酒精挥发，使得酒精温度明显比水的温度低；而在大烧杯的热水中进行实验，由于水温比室温高得多，大烧杯中的热水温度下降很快，加上某些实验者实验操作速度较慢，两次实验的温度实际不相同。

如果水的温度低，因为η水变大，流动时间变大，根据η酒=ρ酒t酒η水/ρ水t水，代入公式的t水是一个偏大的数值，所以最终算出的η酒偏小；相反，如果酒精的温度低，最终算出的η酒偏大。

3.4 粘度计未保持竖直状态带来的误差

由于实验是在大烧杯里做的，有些实验者就把奥氏粘度计斜靠在大烧杯的内壁，使粘度计处于倾斜状态。回顾上文的实验原理：

Q=πr4△p/8ηL，其中Q=V/t，△p=ρgh，

故泊肃叶公式变为V/t=πr4ρgh/8ηL；

若将蒸馏水（标准液体）流动的数据代入上式，得到：

V/t水=πr4ρ水gh水/8η水L水；

将待测液体（酒精）流动的数据代入上式，得到：

V/t酒=πr4ρ酒gh酒/8η酒L酒；

如果两次的液体体积相等，且液柱都是竖直放置，则h水= h酒，L水=L酒。

两个等式相除，得到：η酒=ρ酒t酒η水/ρ水t水

如果粘度计斜放，而且倾斜的角度是随机的，h水=h酒，L水= L酒的条件不存在了，再用η酒=ρ酒t酒η水/ρ水t水计算，当然就有较大误差。

综上所述，只有充分考虑实验中误差产生的原因，改进实验方法，控制实验条件才能减少误差，使实验结果接近真值。

[1]张胜.物理[M].西安：第四军医大学出版社，2005.

G424.31

B

1671-1246（2014）19-0095-03