重水堆停堆工况下单相自然循环流动与传热分析

苑景田，佟立丽，曹学武

（1.上海核工程研究设计院，上海 200233；2.上海交通大学 机械与动力工程学院，上海 200240）

CANDU 6型重水堆停堆工况时，由停堆冷却系统主热传输系统提供强迫循环，排出堆芯热量。停堆工况下冷却剂丧失强迫流动后，堆芯衰变热的排出主要依靠自然循环流动。重水堆主热传输系统设计中，蒸汽发生器的位置高于堆芯，主泵不可用时，可保障建立热虹吸导出堆芯热量［1］。研究［2］发现：重水堆主热传输系统的单相自然循环可在长时间内充当热阱，且不会有燃料包壳失效；堆芯衰变热低于4%时可建立较为稳定的单相自然循环。印度加压式重水堆在停堆低功率工况下，可通过主热传输系统的单相自然循环和蒸汽发生器二次侧作为热阱将主系统温度降低至60 ℃［3］。试验［4］发现，在一定功率水平且每个环路有两台蒸汽发生器可用时，主热传输系统内可建立稳定的单相自然循环。

RELAP5 程序采用两相流体、非平衡模型，是模拟事故瞬态过程较详细的系统程序。已有研究［5-8］表明，该程序在分析反应堆热工水力现象方面也具有较好的可信度。本工作用RELAP5分析研究CANDU 6 型重水堆停堆工况下冷却剂丧失强迫循环后的单相自然循环流动与传热行为。

1 电厂模型及初始条件

CANDU 6型重水堆主热传输系统由两个环路组成，如图1所示。每个环路由2台主热传输泵、2台蒸汽发生器、2个入口集管、2个出口集管和相应的连接管组成，形成一“8”字型。该布置中，每个环路的泵和蒸汽发生器均是串联的，反应堆供水管将燃料通道的入口、出口分别连接到反应堆的入口、出口集管上。蒸汽发生器、主热传输泵和集管位于反应堆的上方，有利于冷却剂产生虹吸自然循环，保证在因主热传输泵失效而事故停堆后，堆芯燃料能得到有效的冷却。

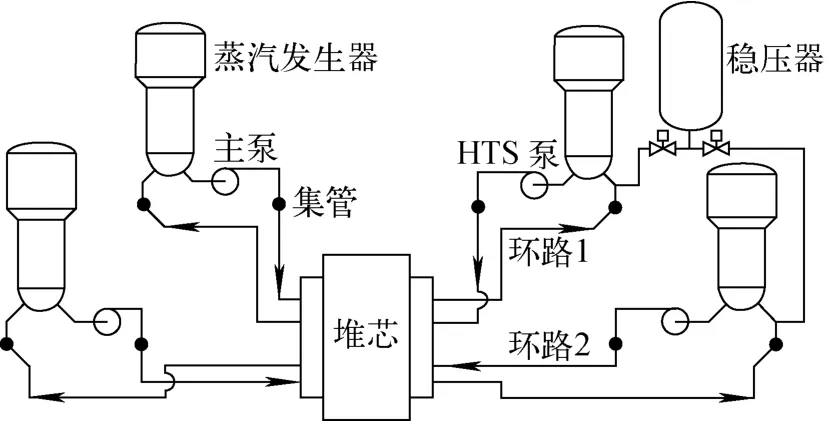
图1 重水堆主热传输系统示意图Fig.1 Schematic diagram of main heat transport system in PHWR

反应堆堆芯为水平布置，380 个燃料通道贯穿堆芯。两个热传输环路分别位于垂直堆芯位置的左右两个半区，每个环路各有190个燃料通道。每个燃料通道内容纳12个燃料棒束，并沿轴向排列，每个燃料棒束有37根环形排列的燃料棒。加压重水在燃料棒束间隙中流过，将燃料元件产生的热量带走。

使用RELAP5建立了重水堆核电厂系统模型（包括主热传输系统和简化的二回路系统），如图2所示。主热传输系统主要模拟堆芯、稳压器、主热传输泵、蒸汽发生器和一回路管道。堆芯模型按照各环路对应的不同流向分为4个流道；轴向分为端部件和燃料组件；堆芯轴向功率分布与实际堆芯轴向功率分布相同；堆芯燃料组件模型包含燃料棒的数量、燃料芯块尺寸、包壳尺寸等。稳压器模型主要由稳压器筒体、连接管线、喷淋系统和卸压系统组成。主热传输泵采用泵部件模拟。蒸汽发生器一次侧模型主要包括进出口水室和U 型管流道；二次侧包括给水进口、下降段、传热区域、汽水分离器、干燥器和蒸汽汽腔。一回路冷却剂管道包括出入口供水管、出入口集管及其他管道。二回路系统模型主要包括主给水系统模型和主蒸汽系统模型：主给水系统模型主要由控制容积和流量控制阀门组成；主蒸汽系统模型模拟蒸汽管道、主蒸汽隔离阀、主蒸汽安全阀和汽轮机等。

图2 重水堆模型节点图Fig.2 Nodalization of PHWR

主热传输系统处于冷态正常装量工况（反应堆停堆3 d 后，反应堆冷却剂温度约为38 ℃）时，堆芯功率变化如图3 所示。假定冷却剂丧失强迫循环后，主热传输系统加压至4 MPa；主热传输系统内冷却剂初始温度为38 ℃；环路内两台蒸汽发生器可用，水装量为38 000kg，并维持不变；蒸汽发生器二次侧完全卸压，维持二次侧压力0.101 MPa。

图3 重水堆停堆后堆芯功率的变化Fig.3 Decay power of core after PHWR shutdown

2 计算分析

2.1 单相自然循环流量

针对环路内蒸汽发生器具备全部输热能力时，对重水堆环路内自然循环流量进行推导，建立该工况下自然循环流量模型。

自然循环流量模型的假定条件为：1）蒸汽发生器U 型管内流体密度呈线性变化；2）流体经过燃料通道后温差较小；3）蒸汽发生器出口处流体与蒸汽发生器二次侧温差较小。

将重水堆内的单个环路简化为图4 的形式，则环路中的浮升力为：

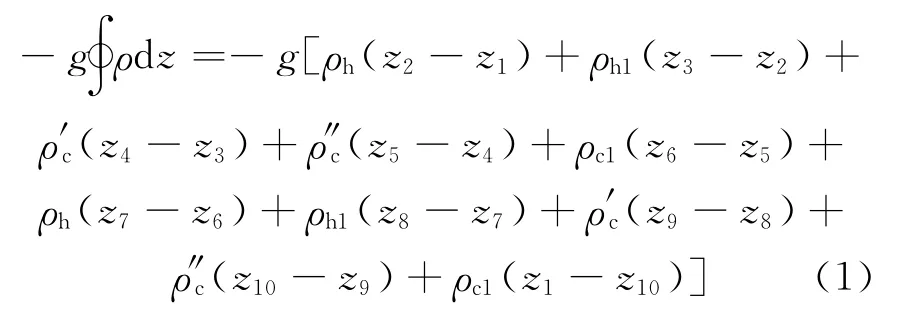
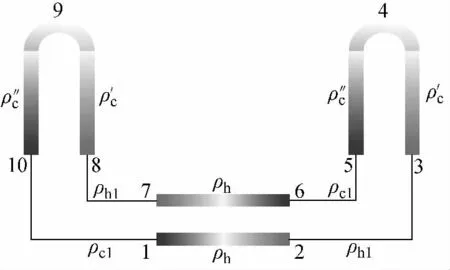
图4 重水堆单个环路简图Fig.4 Schematic of single loop in PHWR

其中：g 为 重 力 加 速 度；ρ 为 流 体 密 度；z 为 高度；z1～z10分别为图4中各点的高度，z1=z2=z6=z7，z3=z5=z8=z10，z4=z9，下标1、6表示燃料通道入口，2、7表示燃料通道出口，3、8表示蒸汽发生器入口，4、9表示蒸汽发生器U 型管顶端，5、10表示蒸汽发生器出口；ρh 为热段流体密度；ρh1为燃料通道出口流体密度；ρc1为燃料通道入口流体密度；ρ′c和ρ″c分别为蒸汽发生器U 型管上升段和下降段流体密度。

式（1）可表示为：

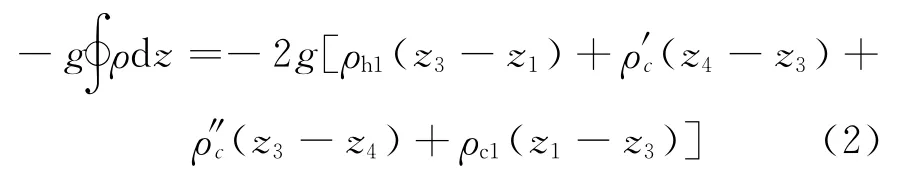
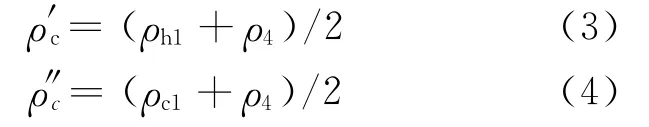
其中，ρ4 为蒸汽发生器U 型管顶端流体密度。

式（2）可表示为：

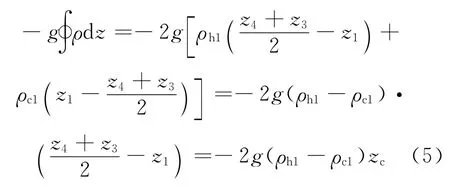
在稳态单相自然循环工况下，系统内的浮升力与系统内的总压降Δp 是平衡的（假定系统内的压降包含摩擦压降和局部压降），即：

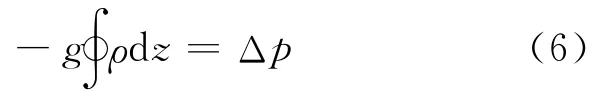
因假定流体经过燃料通道后温差较小，则流体的体积膨胀系数αV可认为是定值：

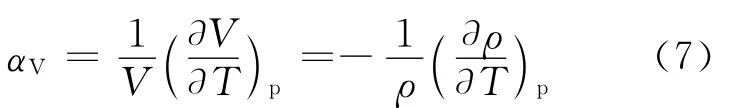
其中：下标p表示定压；T 为流体温度；V 为比体积。

上式积分后为：

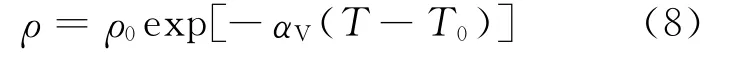
其中，ρ0 为流体温度为T0时的密度。

设T0为蒸汽发生器二次侧大气压力下水的饱和温度，假定流体经过燃料通道后的温差较小，则：

则式（8）可近似为：

因此，堆芯出、入口流体的密度差ρh1-ρc1为：

式（5）可表示为：

其中，ΔTh=Th1-Tc1。

回路内总的压降Δp 为：

其中：fi为第i段的摩擦系数；Li为第i段的通道长度，m；Di为第i 段的通道当量直径，m；ki为第i段的形阻系数；v 为回路内液体的流速，m／s；Ceff为回路总的损失系数为流体在温度为（Th1+Tc1）／2时的密度。

回路内的流速v 可通过蒸汽发生器U 型管内的质量流量W、横截面积Ac来近似获取：

则式（6）为：

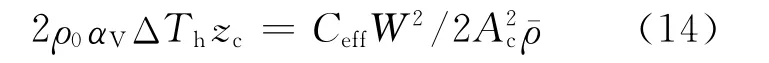
在燃料通道中，有：

其中：Q 为燃料通道功率，kW；cp为水的比定压热容，kJ／（kg·K）。

则回路内的流量为：

对一固定回路，除Ceff外，其余参数均可看作是已知参数，计算Ceff则可得回路内的流量。

在管道长度、管道直径已知的条件下，通过计算各段的摩擦系数和形阻系数来近似确定回路内每段的损失系数。

Lapin［9］在矩形管道分析中充分考虑了上述阻力因素，在其回路内层流条件下总的损失系数计算中采用下式：

其中，Rec为冷却段雷诺数。

Vijayan［10］对8字型环路稳态单相自然循环进行了研究，得出了实验回路的Ceff：

鉴于研究对象的相似性，取式（18）作为重水堆主热传输系统环路的Ceff。将程序计算值与模型计算值相比较，结果如图5 所示。由图5可看出，模型计算的自然循环流量小于程序计算结果，但流量随停堆时间的延长、堆芯衰变功率的降低所呈现的变化趋势与计算结果一致，差异可能是由条件假定以及模型中所采取的近似所引起的。

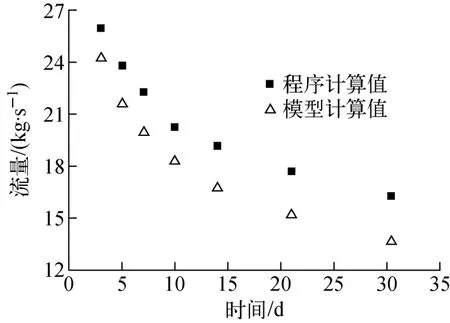
图5 自然循环流量程序计算值与模型计算值比较Fig.5 Comparison of calculation results between code and model for natural circulation mass flow rate

2.2 壁面-流体传热分析

RELAP5中将传热壁面分为竖直壁面和水平壁面，两种壁面对单相流体的自然对流计算分别使用不同的模型。竖直壁面与流体之间的自然对流模型是基于Churchill-Chu模型［11］的：

其中，Ra=GrPr。Churchill-Chu 模型是基于竖直平板壁面得出的，适用于所有层流和紊流的Ra数值范围。

水平壁面与流体自然对流换热时，采用考虑了重力影响因素的McAdams模型［12］：

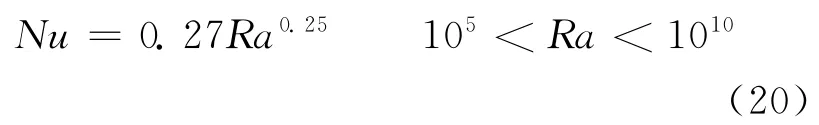
Vijayan［10］在8字型环路自然循环实验研究中，得出了水平、竖直结构壁面对流体的传热模型。

水平加热段：

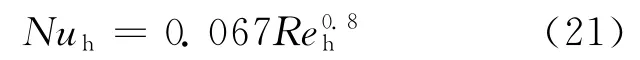
竖直冷却段：

其中，下标h表示加热段，c表示冷却段。

通过建立的重水堆模型，将RELAP5中的Churchill-Chu 模型和McAdams模型分别替换为Vijayan模型，以停堆3d的工况对上述模型进行分析比较，结果示于图6～9。通过比较发现，自然循环建立后，如图6所示，Churchill-Chu模型所得到的U 型管壁面传热系数基本上保持稳定，平均值约为701.3 W／（m2·K）；而Vijayan模型所得到的传热系数在某一值附近持续振荡，其均值约为705.8 W／（m2·K），略高于Churchill-Chu模型的相应值，但差别较小。这也可能是两种模型计算得到的蒸汽发生器出入口处冷却剂的温差几乎无差别（图7）的主要原因。对于包壳对通道内冷却剂的传热系数，自然循环建立后，McAdams模型的传热系数均值约为8 081.0 W／（m2·K），高于Vijayan模型所得到的1 654.9 W／（m2·K）（图8）；两模型传热系数的差异引起两模型计算所得到的包壳温度的差异，前者的包壳温度约为116.1 ℃，后者的包壳温度约为118.4℃（图9）。

图6 U 型管对冷却剂的传热系数比较Fig.6 Comparison of heat transfer coefficient for U tube-to-coolant

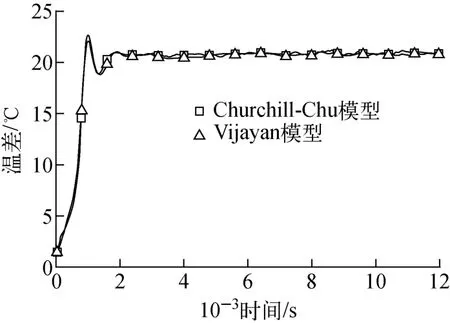
图7 蒸汽发生器出入口温差比较Fig.7 Comparison of temperature difference between SG outlet and inlet plenum

针对环路内两台蒸汽发生器可用的情况，使用Vijayan模型计算的单相自然循环的结果示于图10～12。由计算结果可看出：使用Vijayan模型后，自然循环流量并没有较大的差异（图10）；由于Vijayan模型中包壳对冷却剂的传热系数低于McAdams模型，因此Vijayan模型计算得到的包壳温度略高于原模型的计算值（图11）；而Vijayan模型与Churchill-Chu模型针对U 型管与流体间的传热系数差别较小，因此得到的冷却剂在蒸汽发生器出口处的温度并无明显差别（图12）。

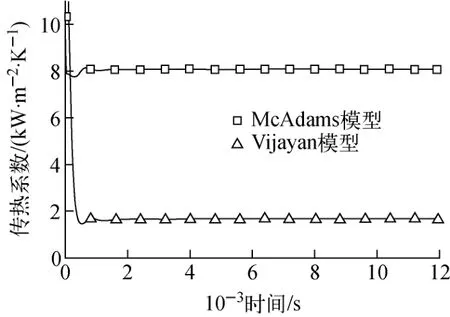
图8 包壳对冷却剂的传热系数比较Fig.8 Comparison of heat transfer coefficient for sheath-to-coolant

图9 包壳温度比较Fig.9 Comparison of sheath temperature

图10 自然循环流量比较Fig.10 Comparison of natural circulation mass flow rate

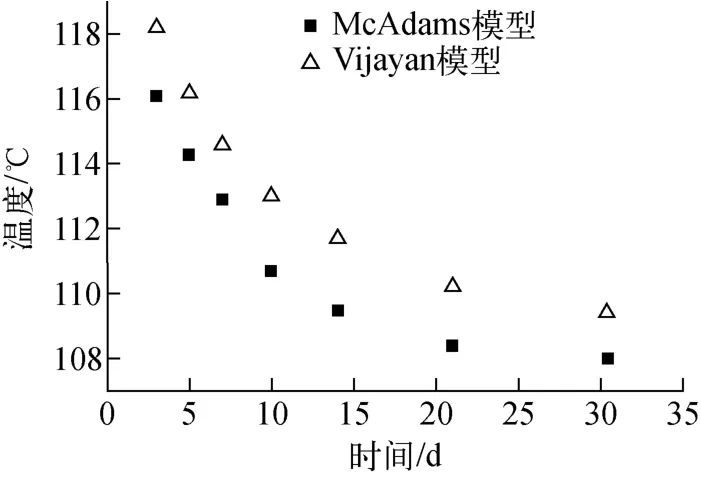
图11 单相自然循环下包壳温度比较Fig.11 Comparison of sheath temperature under single phase natural circle

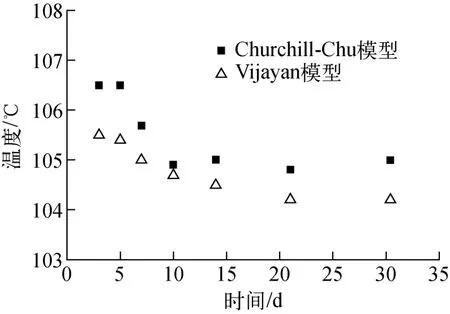
图12 蒸汽发生器出口温度比较Fig.12 Comparison of SG outlet plenum temperature

3 结论

对重水堆主热传输系统在环路内两台蒸汽发生器可用情况下自然循环流量进行了分析，得出了重水堆的单相自然循环流量模型。对程序中的竖直壁面自然对流传热Churchill-Chu模型、水平壁面自然对流传热McAdams模型，分别与Vijayan模型进行了比较分析。通过分析发现，Vijayan模型计算的水平壁面传热系数较McAdams模型的小，因而包壳温度略高，竖直传热系数与Churchill-Chu模型的差别较小，因此蒸汽发生器出口温度无明显差别。

［1］ IAEA.Analysis of severe accidents in pressurized heavy water reactors，IAEA-TECDOC-1594［R］.Vienna：IAEA，2008.

［2］ IAEA.Heavy water reactors：Status and projected development，Technical Report Series No.407［R］.Vienna：IAEA，2002.

［3］ KARUNAKARAN A.Design concepts of safety I＆C systems of 540 MWe PHWR nuclear power plant in India［R］.India：Nuclear Power Corporation of India Ltd.（NPCIL），2005.

［4］ VIJAYAN P K，RAJ V V，PILKHWAL D S，et al.Adequacy of thermosyphon cooling for an Indian PHWR［J］.Current Science，1993，64（3）：175-180.

［5］ KIM I G，LEE S.RELAP5simulation of thermal-hydraulic behavior in a CANDU reactor assessments of RD-14 experiments［J］.Nuclear Technology，2000，130（1）：18-26.

［6］ CHO Y J.Assessments of RELAP5／MOD3.2and RELAP5／CANDU in a reactor inlet header break experiment B9401of RD-14M［J］.Journal of Korean Nuclear Society，2003，35（5）：426-441.

［7］ YUAN Jingtian，TONG Lili，CAO Xuewu.Simulation of quenching in horizontal geometry channel［J］.Nuclear Science and Techniques，2010，21：370-374.

［8］ 苑景田，李京喜，曹学武，等.重水堆燃料通道内浮升力引发的间歇式流动现象数值分析［J］.核动力工程，2011，38（4）：33-36.YUAN Jingtian，LI Jingxi，CAO Xuewu，et al.Simulation of IBIF in HWR horizontal fuel channel［J］.Nuclear Power Engineering，2011，38（4）：33-36（in Chinese）.

［9］ LAPIN Y D.Heat transfer in communicating channels under conditions of free convection［J］.Thermal Engineering，1969，16：94-97.

［10］VIJAYAN P K.Investigations on the singlephase thermosyphon phenomenon in a figure-ofeight loop relevant to pressurized heavy water reactors［D］.Bombay：Indian Institute of Technology，1988.

［11］CHURCHILL S W，CHU H H S.Correlating equations for laminar and turbulent free convection from a vertical plate［J］.International Journal of Heat and Mass Transfer，1975，18（11）：1 323-1 329.

［12］McADAMS W H.Heat transmission［M］.3rd ed.New York：McGraw-Hill，1954.