基于蒙特卡罗-离散纵标双向耦合方法的快中子注量基准分析

袁龙军，陈义学，2，韩静茹

（1.华北电力大学 核科学与工程学院，北京 102206；2.国家核电技术公司 北京软件技术中心，北京 100029；3.环境保护部 核与辐射安全中心，北京 100082）

蒙特卡罗法（MC）和离散纵标法（SN）是最为常用的屏蔽计算方法。蒙特卡罗法可精确模拟复杂几何模型，但计算耗时，尤其对于屏蔽计算中常见的深穿透问题。与蒙特卡罗法相比，离散纵标法计算速度快，但难以精确描述复杂的几何模型。为综合两种方法的优点以解决同时具有复杂几何模型和深穿透问题的屏蔽计算问题，国内外开展了基于蒙特卡罗法和离散纵标法的耦合方法的研究，研制了大量耦合计算程序。目前国内外公开发表的一维耦合程序有HETC96-ANISN［1］、HERMES-ANISN［2］、MCNPANSIN［3］等；二 维 耦 合 程 序 有MCNP-DORT［3］、DORT-MCNP［4］、DORT-PROBEGEN-MCNP［5］、DORT-DOMINO-MORSE［6］等；三维耦合程序有MCNP-TRIDENT［7］、TORT-MCNP［8］等。然而一维和二维耦合程序不能精确计算三维模型，而三维耦合程序仅为单向耦合，在工程计算中不能根据实际情况灵活使用蒙特卡罗法和离散纵标法，严重限制了耦合方法在实际工程中的应用。

为解决上述问题，开发基于蒙特卡罗法和离散纵标法的三维蒙特卡罗-离散纵标双向耦合计算方法，将耦合方法用于压水堆压力容器快中子注量计算，并与基准报告进行比较分析。

1 MC-SN 双向耦合方法

作为辐射屏蔽计算最为常用的两种计算方法，蒙特卡罗法和离散纵标法分别为非确定论方法和确定论方法。实现蒙特卡罗法和离散纵标法耦合计算的关键在于实现蒙特卡罗法模拟的粒子径迹信息和离散纵标法计算的角通量密度间的相互转换，即实现蒙特卡罗模拟粒子的位置、能量和飞行方向与离散纵标法计算的角通量密度的空间网格、能群和离散方向的一一对应转换。

其中，MC粒子径迹信息到SN角通量密度的转换关系［9］为：

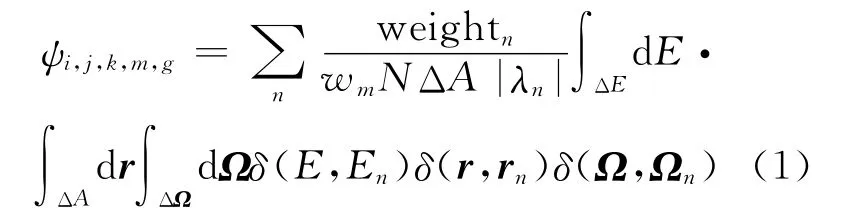
式中：ψi，j，k，m，g为空 间 网 格（i，j，k）处 第g 群 内的m 方向范围内的中子角通量密度；weightn为MC 粒子n 的权重；wm为求积权重系数；N 为MC模拟的源粒子数；ΔA 为给定面元的面积；λn为MC粒子径迹和面法线方向夹角的余弦值；En、rn和Ωn分别为粒子的能量、空间位置和飞行方向。

SN角通量密度到MC 粒子径迹信息的转换关系［10］为：

式中：wm为求积权重系数；ψ（ri，Eg，Ωm）为网格ri、能群Eg和离散方向Ωm区间内的粒子角通量密度；λm为粒子飞行方向与面法线方向夹角的余弦值；Ai为网格区间ri对应的连接面的面积；求和上限I、G 和M 分别为连接面网格数、能群数和离散方向数；p（ri）为MC抽样粒子位于网格区间ri内的概率；p（Eg／ri）为在网格区间ri内抽样、粒子位于能群区间Eg内的概率；p（Ωm／Eg／ri）为在网格区间ri、能群区间Eg内抽样，粒子位于离散方向Ωm内的概率。

根据以上转换方法，通过自主研发的接口程序，实现蒙特卡罗法和离散纵标法的双向耦合，其流程图示于图1，其中MC 程序采用国际通用的粒子输运程序MCNP4C［11］，并采用ENDF60连续能量截面数据库；SN程序采用美国橡树岭国家实验室开发的三维离散纵标程序TORT［12］，采用多群截面库MATXS10。

2 基准验证

为验证三维MC-SN双向耦合屏蔽计算方法的正确性和可靠性，本文采用了BNL（Brookhaven National Laboratory）开 发 的 NUREG／CR-6115［13］压水堆压力容器快中子注量计算基准例题。

基准题的压水堆模型如图2所示。反应堆采用基准题中标准的IN-OUT 堆芯装载模式；堆芯采用204 个燃耗深度不同的组件。基于MC-SN双向耦合方法，并根据基准题模型的特点，选取热屏蔽内表面作为第1耦合面、压力容器堆焊层作为第2耦合面，将模型划分为MC模拟区和SN模拟区，如图2a所示。其计算流程如下。

图1 三维蒙特卡罗-离散纵标双向耦合方法流程图Fig.1 Flow chart of program system for 3D MC-SN bidirectional coupling method

图2 1／8压水堆模型水平（a）和垂直（b）剖面图Fig.2 Horizontal（a）and vertical（b）sections of 1／8PWR model

1）MCNP计算。利用MCNP程序实现堆芯到热屏蔽内表面区域的精确计算，得到第1耦合面的中子径迹信息。

2）MCNP-TORT 计算。通过接口程序，将MCNP程序的粒子径迹信息转换为TORT程序的中子角通量密度，得到用于TORT 计算的边界源文件。

3）TORT 计算。通过边界源文件，利用TORT 程序实现热屏蔽内表面至压力容器焊层的计算。

4）TORT-MCNP 计算。通过接口程序，将TORT 程序的中子角通量密度转换为MCNP程序的粒子概率分布，得到用于MCNP计算的粒子抽样文件。

5）MCNP计算。通过粒子抽样文件，利用MCNP程序实现压力容器内部计算区域的精确计算。

通过以上流程，实现MCNP-TORT 双向耦合计算。

根据基准题模型结构的对称性，本文选取了全堆的1／8作为计算模型，在0°和45°边界采用反射边界，在压力容器外表面和模型顶部及底部采用真空边界。其中压力容器内壁峰值、压力容器1／4壁厚峰值和压力容器内壁焊缝处为计数位置，如图2b所示。

在基准报告中，选取压力容器内壁峰值、1／4壁厚峰值和内壁焊缝处的快中子注量率（E＞1.0 MeV）作为计算区域，并给出MCNP4A及DORT 的计算结果。本文使用单独的MCNP4C 程序和MCNP-TORT 双向耦合程序进行相应计算，得到了对应的计算结果，并与基准报告进行对比，如图3所示。

从图3可看出，耦合程序计算结果与基准结果符合良好，平均相对误差不超过3%；与MCNP4A结果相比，最大相对误差不超过10%。

通过对比，较SN程序，MCNP-TORT 双向耦合程序计算结果与基准结果更为吻合。

在相同的计算时间下，MCNP-TORT 双向耦合程序较单一MCNP程序统计误差更小，计算结果可靠性更强。单一MCNP 程序计算耗时53min，模拟粒子数为1.5 亿，统计误差为3%左右。MCNP-TORT 双向耦合程序的计算时间为48min，其中两次MCNP计算分别耗时12min和23min，模拟粒子数分别为5 000万和9 000万，统计误差均为1%左右；TORT 计算耗时13min。

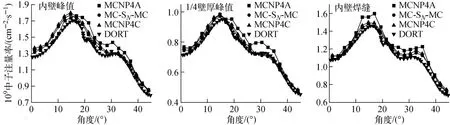
图3 压力容器内壁峰值、1／4壁厚峰值和内壁焊缝处的快中子注量率（E＞1.0 MeV）周向分布Fig.3 Circular distributions of E＞1.0 MeV fast neutron fluence rate at pressure vessel inner wall axial peak location，pressure vessel 1／4axial peak location and pressure vessel lower weld

3 结论

为解决同时具有复杂几何和深穿透问题的屏蔽计算问题，开发了基于三维蒙特卡罗-离散纵标双向耦合方法。本文将此耦合计算方法应用于NUREG／CR-6115压水堆压力容器快中子注量计算，并与基准报告中其他计算方法进行对比，结果符合良好；在相同的计算时间下，耦合计算程序统计误差优于单一蒙特卡罗程序，可靠性更强，验证了三维蒙特卡罗-离散纵标双向耦合方法的正确性与可靠性。

［1］ GABRIEL T A.CALOR：A Monte Carlo program package for the design and analysis of calorimeter systems，ORNL／TM-5619［R］.USA：ORNL，1977.

［2］ CLOTH P，FILGES D，NEEF R D，et al.HERMES：A Monte Carlo program system for beam-materials interaction studies［R］.Germany：KFA，1988.

［3］ GALLMEIER F X，PEVEY R E.Creation of a set of interface utilities to allow coupled Monte Carlo／discrete ordinate shielding analysis［C］∥Third International Topical Meeting on Nuclear Applications of Accelerator Technology.USA：American Nuclear Society，1999：404-409.

［4］ 郑征，吴宏春，曹良志.蒙卡与SN耦合方法在压水堆堆腔漏束计算中的应用［C］∥第十一届全国蒙特卡罗方法及应用学术交流会.绵阳：［出版者不详］，2012.

［5］ EGGLESTON J E，ABDOU M A，YOUSSEF M Z.The use of MCNP for neutronics calculations within large buildings of fusion facilities［J］.Fusion Engineering and Design，1998，42：281-288.

［6］ EMMETT M B，BURGART C E，HOFFMAN T J.DOMINO：A general purpose code for coupling discrete ordinates and Monte Carlo radiation transport calculations，ORNL-4853［R］.USA：Oak Ridge National Laboratory，1973.

［7］ URBAN W T，SEED T J，DUDZIAK D J.Nucleonic analysis of a preliminary design for the ETF neutral-beam-injector duct shielding，LAUR-80-2926［R］.New Mexico：Los Alamos Scientific Laboratory，1980.

［8］ KUROSAWA M.TORT／MCNP coupling method for the calculation of neutron flux around a core of BWR［J］.Radiation Protection Dosimetry，2005，116（1-4）：513-517.

［9］ CHEN Y，FISCHER U.Program system for three-dimensional coupled Monte Carlo-deterministic shielding analysis with application to the accelerator-based IFMIF neutron source［J］.Nuclear Instruments and Methods in Physics Research A，2005，551：387-395.

［10］HAN Jingru，CHNE Yixue，YUAN Longjun，et al.Validation of three-dimensional coupled discrete ordinates-Monte Carlo program system through shielding benchmark analysis［R］.［S.l.］：ICETCE，2012.

［11］BRIESMEISTER J F.MCNP：A general Monte Carlo N-particle transport code，version 4C，LA-13709-M［R］.USA：Los Alamos National Laboratory，2000.

［12］RHOADES W A，SIMPSON D B.The TORT three-dimensional discrete ordinates neutron／photon transport code，ORNL／TM13221［R］.USA：Oak Ridge National Laboratory，1997.

［13］CAREW J F，HU K，AROSON A，et al.PWR and BWR pressure vessel fluence calculation benchmark problem and solutions［R］.Washington D.C.：Brookhaven National Laboratory，2001.