BP神经网络在AP1000核电站事故诊断应用中的初步研究

赵云飞，张立国，童节娟，张 勤，曲静原

（清华大学 核能与新能源技术研究院，北京 100084）

随着现代社会中系统复杂性越来越高，人们对其智能化有了更高的要求，人工神经网络能表达复杂系统内的复杂非线性关系，为提高大型复杂系统的智能化提供了一条途径。McCulloch和Pitts早在1943年就为人工神经网络做出了开拓性的工作，Rumelhart和McCelland等在1986年提出多层网络的误差反向传播学习算法，简称BP算法［1］。BP神经网络是前向型神经网络的核心，已被应用于复杂系统的模式识别、故障诊断和预报［2-4］等领域。

核电站一般由压力容器、一回路冷却剂系统、二回路蒸汽发生器、汽轮机、发电机等组成，另外还包括一回路注入系统等许多安全设施。自美国三哩岛事故和前苏联切尔诺贝利事故后，核电站提高了其安全系统的冗余性，这也进一步增加了其复杂性，日本福岛核事故后，核电站的复杂性势必进一步增加。核电站发生事故时，始发事件与电站响应之间存在非常复杂的关系，仅凭操作员自身很难准确判断事故类型或造成判断错误，这阻碍了下一步应急行动。核电站发生事故后，如何快速准确诊断出事故类型一直受到人们的关注并得到广泛研究，这其中包括基于模糊推理、遗传算法和人工神经网络诊断传统轻水堆核电站事故［5-7］，不过BP神经网络用于AP1000核电站事故诊断还没有过深入研究。

本文利用神经网络能方便表达复杂系统非线性关系的优点，将其应用于第三代AP1000核电站核应急中的事故诊断。本文首先简单介绍BP神经网络，然后分析AP1000 核电站的部分事故序列，并收集这些事故序列中的电站参数数据，在此基础上建立BP神经网络模型，利用一部分数据训练网络，剩余数据作为测试数据以验证网络模型诊断结果的准确性。

1 BP神经网络

BP神经网络模拟人脑中神经元的工作原理，包含输入层、隐藏层和输出层，每层由若干神经元组成，各层之间的神经元通过权值连接，如图1所示。

BP神经网络学习过程中采用误差反向传播算法，这种算法的一次迭代包含正向过程和反向过程，正向过程中根据输入层各节点输入和各层神经元之间的连接权值计算输出层各节点输出，并与精确值比较得到输出层误差，反向过程中根据输出层误差层层递进修正各层神经元之间的权值，直到输入层与第1隐藏层之间的权值修正完毕。重复正向过程和反向过程，直到网络的正向输出结果与精确值之间的误差小于设定值。

为表达输入和输出之间的非线性关系，各层之间可采用非线性传递函数，如logistic函数和双曲正切函数。隐藏层可为1层或多层，不过在实际应用中，1 层隐藏层，即3 层的BP神经网络即可满足拟合输入与输出关系的要求。在标准BP 神经网络基础上做了很多优化，包括权值修正算法、训练过程中改变学习率等，这些极大提高了BP 神经网络的拟合能力和训练速度［1］。

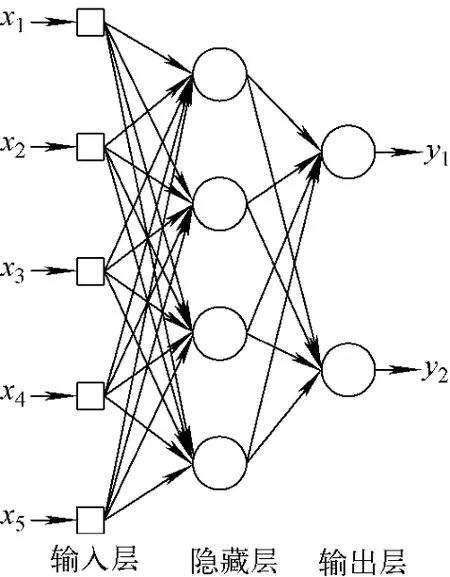
图1 BP神经网络示意图Fig.1 Schematic diagram of BP neural network

2 AP1000核电站事故分析

相比于传统的轻水堆核电站，AP1000 核电站在设计上更多的采用重力、自然循环等非能动思想，所以事故分析及电站响应与传统核电站有所不同。AP1000 核电站安全分析报告分析了各种类型的事故，包括一回路系统热量载出增加、二回路热量载出减少、反应堆冷却剂系统流量减少、反应堆冷却剂装量 增 加 及 减 少 等［8］。作 为BP 神 经 网 络 在AP1000核电站事故诊断中的初步研究，本文选取了其中的4 种事故：蒸汽发生器（SG）泄压阀或安全阀误开启事故；蒸汽系统管道破口事故；丧失正常给水事故；给水管道破口事故。

以蒸汽发生器泄压阀或安全阀误开启事故为例说明事故发生后核电站的响应。蒸汽发生器泄压阀或安全阀误开启事故是一回路系统热量载出增加类型事故之一，将导致二回路蒸汽流量先增加后减小，因为从一回路系统的热量载出增加，所以一回路系统温度和压力下降，同时由于慢化剂的负温度反应性系数，导致堆芯反应性升高。主要的安全保护措施有：堆芯补水箱触发；由功率过高触发的反应堆停堆；主给水管道隔离；启动给水系统隔离；主蒸汽管道隔离阀关闭。

通过分析这4种事故，选取了分析结果中9个电站响应参数，这9个参数分别是核功率、一回路压力、环路1堆芯入口温度、环路1堆芯出口温度、环路2堆芯入口温度、环路2堆芯出口温度、稳压器内水量、环路1 蒸汽发生器压力、环路2蒸汽发生器压力。图2为蒸汽发生器安全阀误开启事故中一回路压力和环路1温度变化曲线。

3 BP神经网络建模及试验分析

3.1 BP神经网络建模

基于MATLAB中BP 神经网络工具箱建立用于AP1000事故诊断的网络模型［9］。网络中输入节点有9个，分别对应9个电站响应参数。输出节点，即要诊断的事故类型有4个，分别对应蒸汽发生器泄压阀或安全阀误开启事故、蒸汽系统管道破口事故、丧失正常给水事故和给水管道破口事故，若输出节点对应的事故发生，则输出为1，否则为0。由AP1000安全分析报告，针对每种事故，本文提取了事故发生后601个时刻（时间间隔为1s）的电站响应参数值，因为这些参数单位和量级不同，所以在输入到神经网络前首先进行归一化处理，处理公式如下：

其中：P 为原始参数值；Pmin和Pmax分别为每个参数的最小值和最大值；P′为归一化后的参数值，范围为0～1。

网络中设置1个隐藏层，因为隐藏层中神经元数的设定无统一公式，为更准确地拟合输入和输出之间的关系，本文设定31个隐藏层神经元。

隐藏层的传递函数采用对数正切函数，输出层的传递函数采用logistic函数，本文中采用trainlm 函数对网络进行训练。网络模拟性能由模拟结果与精确值之间的均方误差表示，网络训练的终止可由以下决定：迭代次数达300次；或模拟结果的均误方差小于10-4；或误差曲面的梯度小于10-7。为最大程度地实现对各种事故特征的拟合，选取神经网络的训练数据和测试数据时按事故后时间顺序，每隔5组数据选取1 组测试数据，剩余数据为训练数据，这样所有的电站响应参数中的2 004组作为样本训练神经网络，利用剩余的400组数据作为测试数据验证网络模拟结果的准确性。

3.2 BP神经网络模拟试验分析

网络训练过程中模拟结果与精确值之间的均方误差与迭代次数的关系示于图3。迭代次数达到300次时迭代终止，最终的均方误差为0.000 131 64，由图3可见，迭代开始阶段均方误差下降很快，并逐渐减慢，迭代次数达到200次后，均方误差下降已经很慢，可认为在200次时已达到迭代收敛。

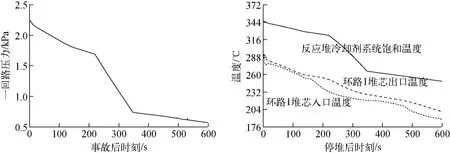
图2 蒸汽发生器安全阀误开启事故中一回路压力和环路1温度变化曲线［8］Fig.2 Curves of RCS pressure and loop 1temperature in inadvertent opening of steam generator safety valve accident［8］

利用训练好的神经网络对400组测试数据进行模拟，模拟结果与精确值的比较表明，神经网络对400 组测试数据均能做出正确诊断。BP神经网络中均方误差的定义为：

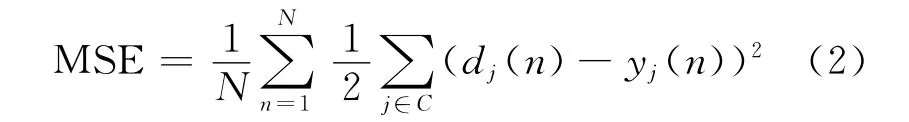
其中：N 为测试数据组数，N=400；C 为4个网络输出的集合；dj（n）和yj（n）分别为第n 组数据输出节点j 的精确值和网络模拟值。经过计算，400组模拟结果与精确值之间的均方误差为1.326×10-6。表1列出了部分比较结果。

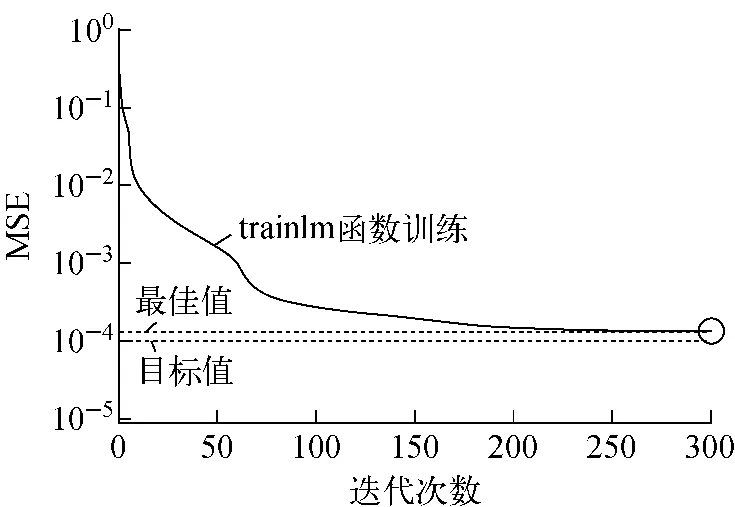
图3 神经网络训练过程Fig.3 Neural network training process

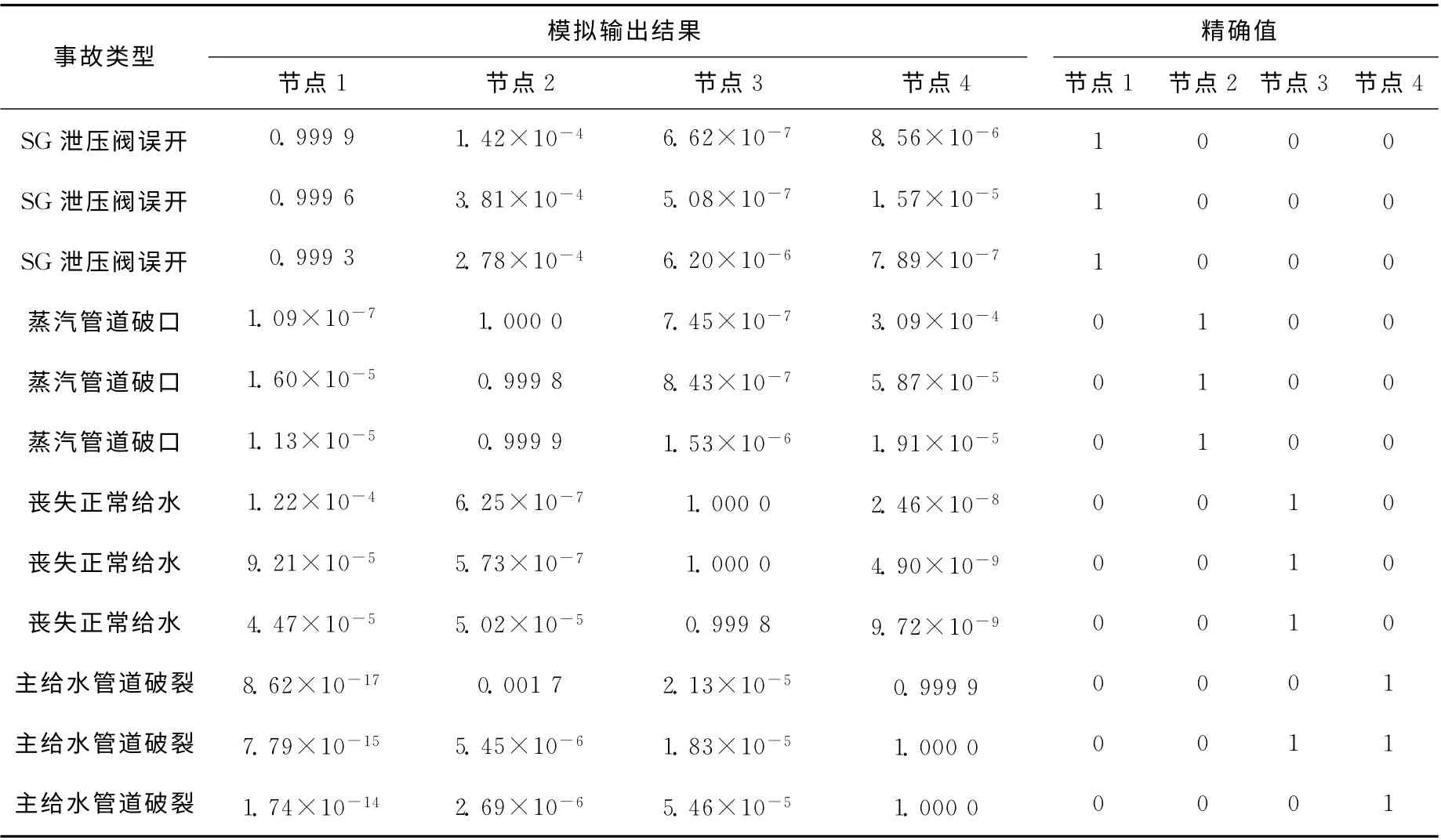
事故类型模拟输出结果 精确值节点1 节点2 节点3 节点4 节点1 节点2 节点3 节点4 SG 泄压阀误开SG 泄压阀误开SG 泄压阀误开蒸汽管道破口蒸汽管道破口蒸汽管道破口丧失正常给水丧失正常给水丧失正常给水主给水管道破裂主给水管道破裂主给水管道破裂0.999 91.42×10-46.62×10-78.56×10-6 0.999 63.81×10-45.08×10-71.57×10-5 0.999 32.78×10-46.20×10-67.89×10-7 1.09×10-71.000 07.45×10-73.09×10-4 1.60×10-50.999 88.43×10-75.87×10-5 1.13×10-50.999 91.53×10-61.91×10-5 1.22×10-46.25×10-71.000 02.46×10-8 9.21×10-55.73×10-71.000 04.90×10-9 4.47×10-55.02×10-50.999 89.72×10-9 8.62×10-170.001 72.13×10-50.999 9 7.79×10-155.45×10-61.83×10-51.000 0 1.74×10-142.69×10-65.46×10-51.000 0 111000000000 000111000000 000000111010 000000000111

4 结论

本文基于AP1000安全分析报告中分析的事故序列，利用MATLAB 中的BP 神经网络工具箱建立了用于AP1000核电站事故诊断的网络模型，利用对AP1000安全分析报告进行事故分析得到的2 004组数据训练网络，以事故分析得到的其他400组数据为测试数据，验证训练得到的网络在事故诊断中的准确性，结果表明神经网络能准确诊断这400组数据对应的事故类型。

本工作是对BP 神经网络在AP1000核电站事故诊断中应用的初步研究，分析的事故局限于AP1000安全分析报告中的部分事故，若要对AP1000核电站事故诊断建立1套完整的BP神经网络模型，需分析更多的事故，并以此来训练网络模型。另外本文对BP神经网络的各项参数也未进行很详细的研究，这些参数可能对网络的训练过程及网络模型在事故诊断中的鲁棒性有一定影响，不过本文仍对后续基于BP神经网络建立核电站事故诊断智能化系统的工作做出了初步探索并打下了一定基础。

［1］ HAYKIN S.Neural networks：A comprehensive foundation［M］.2nd ed.London，UN：Prentice Hall，1999.

［2］ GUPTA C N，PALANIAPPAN R，SWAMINATHAN S，et al.Neural network classification of homomorphic segmented heart sounds［J］.Applied Soft Computing，2007，7：286-297.

［3］ SUN Yanjing，ZHANG Shen，MIAO Changxin，et al.Improved BP neural network for transformer fault diagnosis［J］.Journal of China University of Mining ＆Techonology，2007，17（1）：138-142.

［4］ ZHANG Yudong，WU Lenan.Stock market prediction of S ＆ P 500via combination of improved BCO approach and BP neural network［J］.Expert Systems With Applications，2009，36：8 849-8 854.

［5］ LEE M.Expert system for nuclear power plant accident diagnosis using a fuzzy inference method［J］.Expert Systems，2002，19（4）：201-207.

［6］ 周杨平，赵炳全.基于遗传算法和知识库的核电厂故障诊断方法［J］.核动力工程，2000，21（4）：362-367.ZHOU Yangping，ZHAO Bingquan.Method of fault diagnosis in nuclear power plant based on genetic algorithm and knowledge base［J］.Nuclear Power Engineering，2000，21（4）：362-367（in Chinese）.

［7］ SANTOSH T V，VINOD G，SARAF A K，et al.Application of artificial neural networks to nuclear power plant transient diagnosis［J］.Reliability Engineering and System Safety，2007，92：1 468-1 472.

［8］ AP1000final safety evaluation report［R］.US：NRC，2004.

［9］ 张德丰.MATLAB神经网络应用设计［M］.北京：机械工业出版社，2009：61-69.