一体化汽-气稳压器动态特性研究
吴 磊,贾海军,刘 洋,马喜振
(清华大学 核能与新能源技术研究院 先进反应堆工程与安全教育部重点实验室,北京 100084)
一体化压水反应堆将主换热器或蒸汽发生器、主循环泵、稳压器等主回路核心装置布置在反应堆压力容器内。此种布置消除了传统的冷却剂回路管道,结构紧凑,避免大LOCA,大幅提高了反应堆的安全性。汽-气稳压器具有自稳压特性,其因结构简单、省去了加热和喷淋装置、防止容积沸腾等特点而在一体化反应堆以及其他类型中小型反应堆中得到应用。清华大学自主开发设计的NHR 系列等即是采用汽-气稳压器的一体化压水反应堆的典型代表[1]。近年来,NHR 系列的热工参数逐步提升,以适用于城市集中供热、生产工业蒸汽、海水淡化等非发电领域。稳压器的稳压能力和动态特性对整个反应堆一回路系统的安全性有重要影响,需要对其进行深入研究。
当前,对汽-气稳压器的动态特性进行了一些实验和理论研究。Leonard 等[2]对汽-气稳压器涌入过程进行实验研究,重点考察了不同种类非凝结性气体,不同的气体组分以及分层现象等对稳压特性的影响。Hassan等[3]进一步改进和发展了Relap5程序中相关计算模型。2006年,Ambrosini等[4]对汽-气稳压器内存在的传热传质理论进行总结并指出,可基于不同的表达式来归纳多种形式的传热传质比拟方法。Kim 等[5]通过实验的方法考察了在高压下有非凝结性气体存在时的冷凝传热系数,并发展了高压下的汽-气稳压器模型[6]。
本文主要是建立汽-气稳压器计算模型,通过与汽-气稳压器涌入实验数据进行比较,验证模型的可靠性,同时基于此模型对采用一体化汽-气稳压器的NHR-Ⅱ系统的稳压动态特性进行研究,揭示NHR-Ⅱ系统功率调节过程中压力和温度跟随滞后对系统压力变化的影响机理。
1 理论模型
汽-气稳压器通过压缩非凝结性气体和蒸汽的混合物进行稳压,一般布置在一体化压水反应堆顶端。汽-气稳压器按照工质特性分为3个区:气相混合区、气液相界面区和液相区,如图1所示。上部的气相混合区主要包含非凝结性气体和蒸汽的混合物,由气体和水蒸气的分压决定非凝结性气体与蒸汽的含量比值;下部的液相区主要是对应蒸汽分压的饱和水;气液界面是气液混合区域。在动态条件下,冷凝、扩散、蒸发、自然对流等共同决定汽-气稳压器内部物理现象的复杂性。

图1 一体化汽-气稳压器区域划分Fig.1 Three regions in integrated gas-steam pressurizer
本文数学模型是通过求解不同的场方程来获得整个系统描述需要的压力(p)、相比内能(Ug,Uf)、空泡份额(αg)、相速度(vg,vf)、非凝结性成分含量(Xg)等变量,独立变量为时间(t)和距离(x)。提出以下假设:假定在汽-气混合区域内非凝结性气体和水蒸气具有同样的速度和温度,即vn=vs、Tn=Ts,其中vn和vs分别为非凝结性气体和水蒸气速度,Tn和Ts分别为非凝结性气体和水蒸气温度,并认为蒸汽和非凝结性气体的混合物仍处于热力学非平衡态条件。
基于气相和液相基本的质量、动量和能量守恒方程,在有非凝结性气体的存在下,需要添加或修正传热传质项,并对相关物理模型进行建模计算。主要包括以下内容:
质量方程添加项:当有非凝结性气体存在时,质量守恒方程会随着非凝结性气体的种类N 增加N-1个,形式如下:
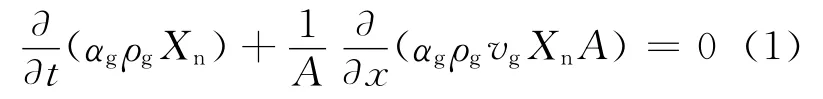
其中:ρg 为气相密度;Xn为气相中非凝结性气体的含量;A 为通道横截面积。
能量方程添加项:当有非凝结性气体存在时,能量守恒方程中添加了界面直接加热项Qgf(式(3))。界面相关项的定性温度采用主流的蒸汽分压所对应的饱和温度,而非局部对应的界面蒸汽分压对应的饱和温度。
动量守恒方程:基本形式未改变,只是在有非凝结性气体存在时将所有场方程中蒸汽物性参数采用蒸汽/非凝结性气体混合物物性参数代替。
界面冷凝的处理:通过Colburn-Hougen迭代方法计算蒸汽和液相表面温度,应用此温度于热流密度关系式;在气体湍流状态或非凝结性气体存在时,采用Vierow 和Schrock提出的基于Nusselt层流冷凝系数的修正因子。
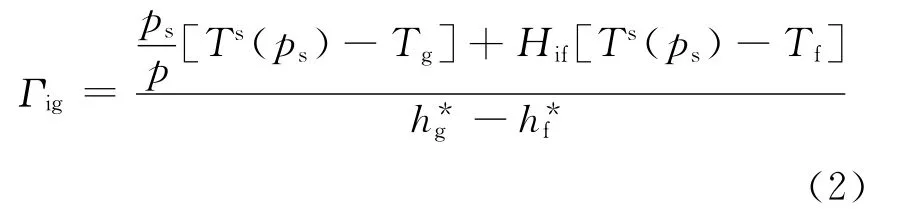
相界面质量的交换处理:主要是用气相分压参数代替系统总压对应参数。相界面交换的质量为:其中:Γig为相界面交换的质量;ps为水蒸气分压;Ts(ps)为水蒸气分压对应的饱和温度;Tg和Tf分别为气相温度和液相温度;h*g和h*f分别为气相焓和液相焓;Hif为界面与液相间传热系数。
相界面能量的交换处理:有非凝结性气体存在时主流之间的热量交换为:

其中:pn为非凝结性气体分压;Hgf为气液相间直接传热系数。
当非凝结性气体存在时,界面的热量传递和质量传递都需进行修正,能量方程中用到h*g和Γig,采用蒸汽分压代替总压。
混合相物性参数处理:有非凝结性气体存在时,水蒸气的参数直接查水蒸气参数表,将非凝结性气体当作理想气体处理,采用修正的Gibbs-Dalton混合物计算方法。
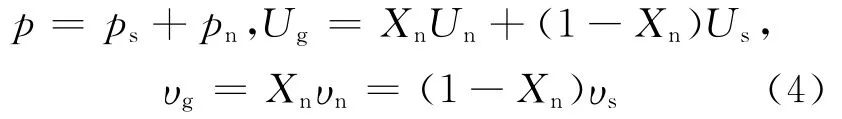
其中:Us和Un分别为水蒸气和非凝结性气体比内能;υs和υn分别为水蒸气和非凝结性气体比体积;υg为气相比体积。
扩散系数的计算采用Fuller方法[7]:
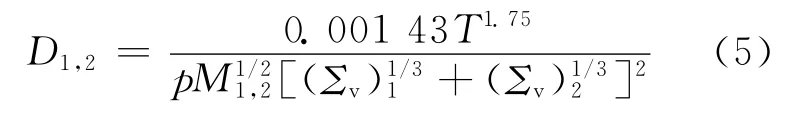
其中:D1,2为 扩 散 系 数;M1,2=2(1/M1+1/M2)-1,为平均相对分子质量;Σv为原子扩散体积。
2 模型验证
选择麻省理工学院进行的汽-气稳压器内涌入波动实验进行模型的验证分析[2],主要考察汽-气稳压器压力响应特性。N2作为非凝结性气体且质量分数分别为0%、10%、20%,实验条件列于表1。
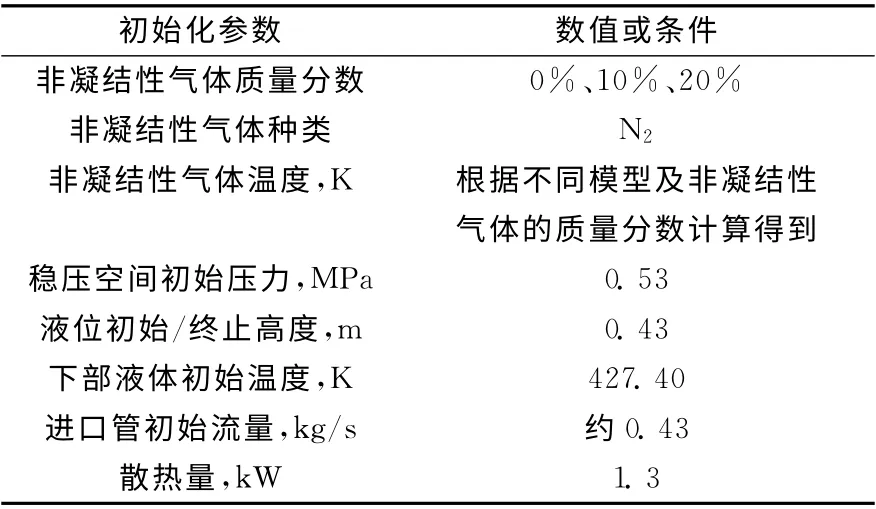
表1 验证实验条件Table 1 Verification experiment conditions
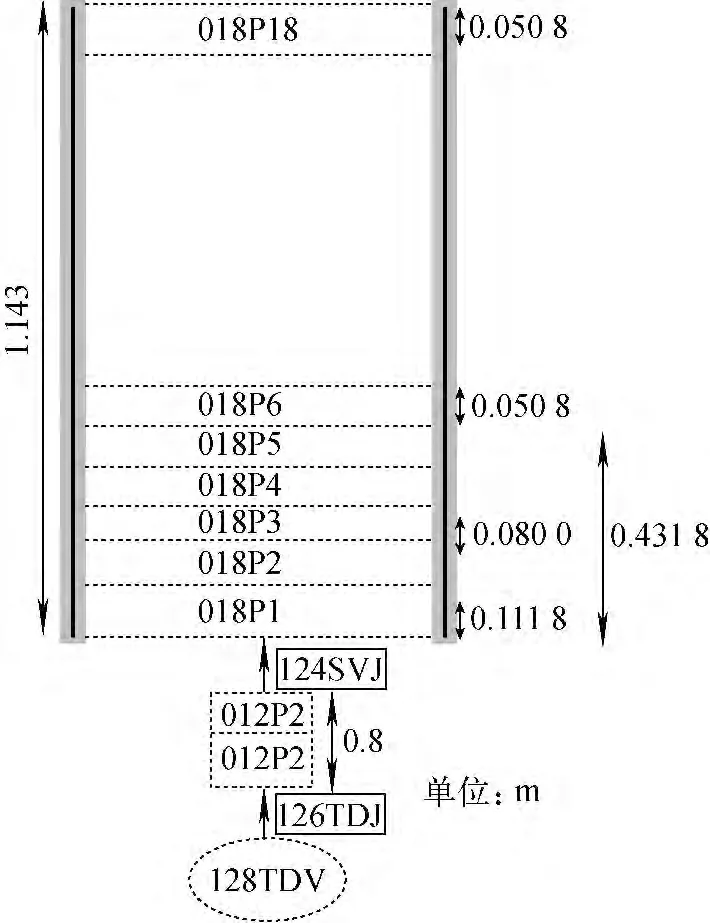
图2 验证性实验系统节点划分Fig.2 Nodalization of experimental system
实验装置的节点划分如图2所示。实验水箱用控制体018表示,划分为18个小控制体,并通过管道012与时间控制体128连接,边界条件根据实验数据以流量为时间函数形式给出。初始化条件列于表1。由于N2和水蒸气(H2O)的相对分子质量相差不大,初始化时将N2和水蒸气视为平衡态的均匀混合性气体处理。计算结果如图3所示。
图3a为N2质量分数为0%时的压力变化。过程维持时间约34.8s,计算得到系统压力从初始的0.53 MPa随过冷水的涌入逐步上升到峰值0.64 MPa,与实验结果基本一致,峰值相对误差为0.94%。N2质量分数为10%和20%的模拟和实验结果如图3b、c所示。计算得到系统压力从0.53 MPa分别升至0.79 MPa和0.91 MPa 的峰值,平均上升速率分别为0.007 3和0.011 MPa/s。与实验结果对比可知,峰值相对误差分别为8.78%和12.89%,均在15%以内,具有较好的一致性。
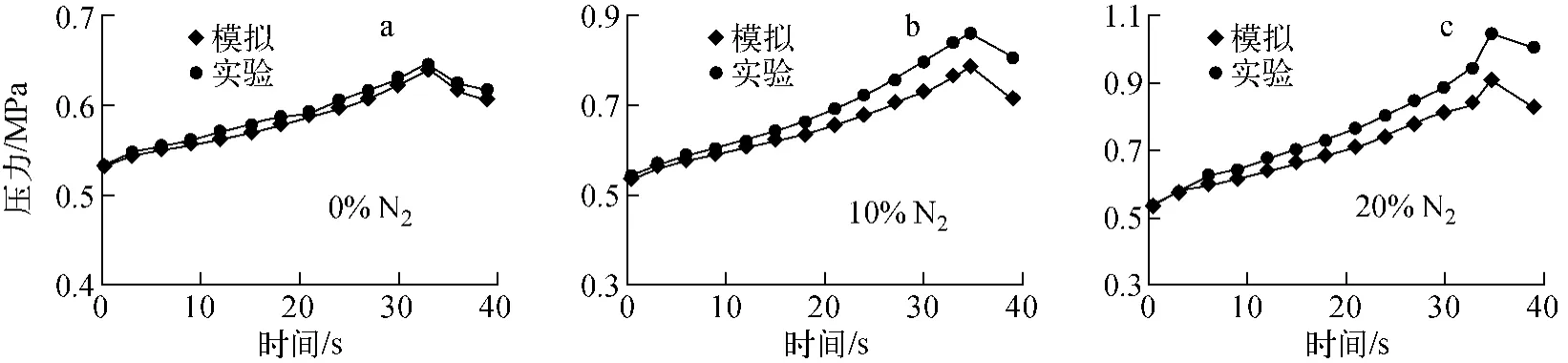
图3 系统压力变化Fig.3 Pressure response with nitrogen
由图3可知,计算模型可对非凝结性气体存在条件下的稳压特性进行较好的预测,误差值在工程应用允许范围内。随N2质量分数的增加,系统压力峰值和压力增加速率均增加,这说明非凝结性气体的存在抑制热量的散失或传递,且这种抑制作用随着非凝结性气体质量分数的增加而增强。
3 NHR-Ⅱ汽-气稳压动态特性
根据前文研究可知,理论模型能对汽-气稳压器稳压动态特性进行较好的预测。基于上述计算模型,进一步研究采用一体化汽-气稳压器和全功率自然循环的NHR-Ⅱ系统稳压动态特性。
3.1 系统参数及动态过程介绍
主要考察NHR-Ⅱ系统功率线性迅速增加等反应堆系统极端运行工况。功率调节具体过程如下:功率从0s开始保持30%直到1 000s,使得整个NHR-Ⅱ系统稳定,然后在60s内线性增加到100%,功率保持稳定至5 000s,整个过程结束。整个动态过程中,一、二回路采用运行控制方案为主回路平均温度不变的方案,即主回路堆芯进出口温度平均值保持不变,同时保证二回路压力不变,而二回路流量增大,进口温度下降。具体参数列于表2。
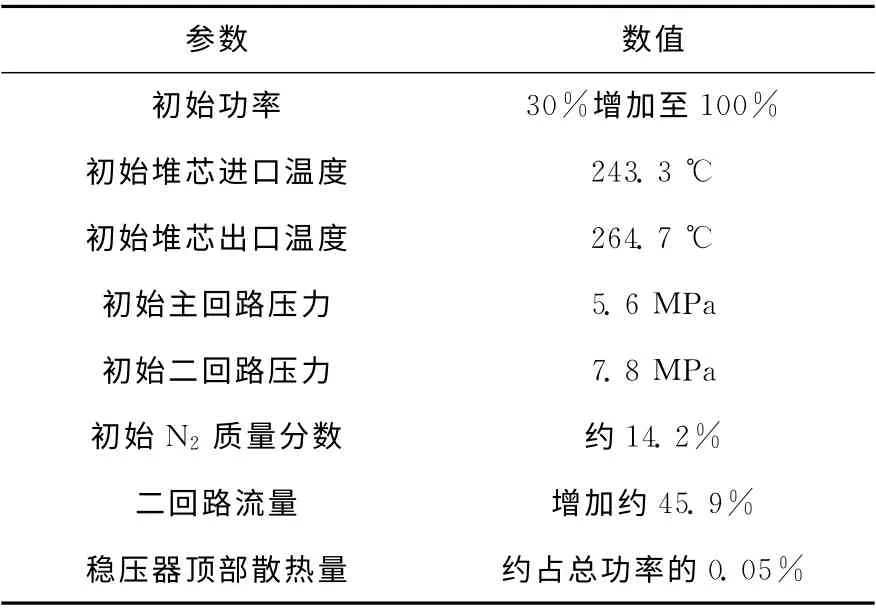
表2 NHR-Ⅱ动态调节过程热工参数Table 2 Operation parameters and conditions in NHR-Ⅱ
3.2 系统节点划分
系统节点划分如图4、5所示。控制体014表示堆芯流通通道,与之相邻的热构件是堆芯燃料棒;控制体026 表示稳压空间,即一体化汽-气稳压器,划分为10个控制体;控制体024为分支,分别连接稳压器、主换热器、上升段;013、015、017共同表示节流件,进行系统阻力控制和自然循环流量调节;部件PHE 表示主换热器;二回路的进出口分别由时间控制体连接,给出二次侧流量、温度、压力等参数;初始化条件列于表2。
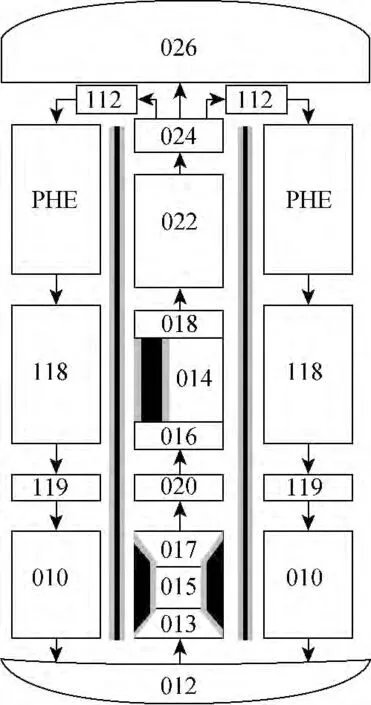
图4 NHR-Ⅱ系统节点划分Fig.4 Nodalization of NHR-Ⅱsystem
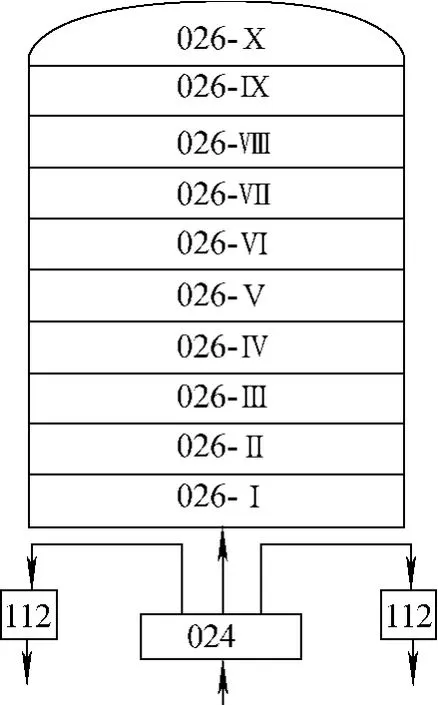
图5 稳压器节点划分Fig.5 Nodalization of pressurizer
3.3 结果分析
1)系统压力变化特性
由于NHR-Ⅱ采用全功率自然循环和一体化汽-气稳压器设计,在动态运行过程中对压力跟随变化特性具有较高的要求。在功率快速提升过程中,重点关注系统压力的变化。
(1)压力变化影响因素
在功率调节的动态过程中,稳压器下部的液体体积和稳压器内的温度变化,主要决定着系统压力的变化。选定涌入或涌出稳压器内流体质量和稳压器内温度进行定量分析。
涌入稳压器流体直接压缩稳压空间内的汽-气混合物,改变其内部温度以及物质组分分布,对压力的变化具有重要的影响。图6为涌入稳压器流体质量随时间的变化。
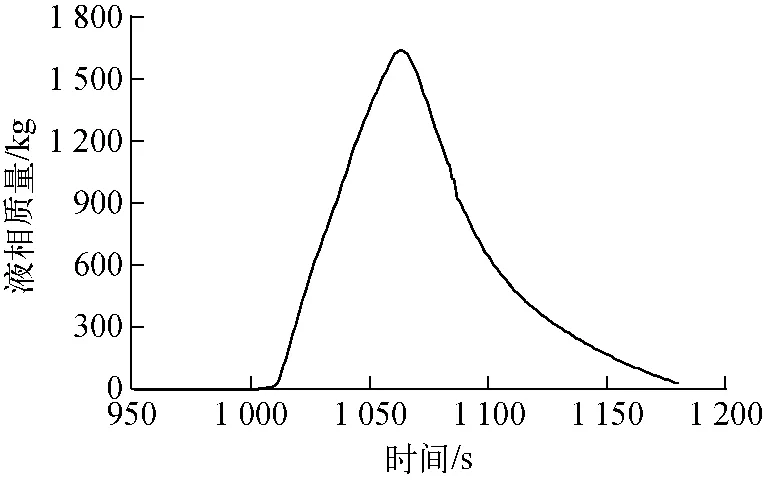
图6 涌入稳压器流体质量随时间的变化Fig.6 Mass of liquid surged into pressurizer vs time
初始阶段,功率保持在30%,涌入稳压器的液相质量约为0kg。在功率提升初始阶段(1 000~1 013s),功 率 从30%线 性 增 加 到45%,涌入稳压器的流体仍基本为0kg;在接下来功率提升的47s(1 014~1 060s),流体涌入稳压器内部的质量近线性增加,且涌入稳压器的质量最大值出现在1 060s,约为1 625kg;在功率稳定在100%阶段,涌入稳压器的液相质量逐渐减少,最终稳定在某一数值。这表明,在此阶段开始有部分液相涌出稳压器,主要是由于二回路冷却能力的增强使主回路平均温度降低和压缩反冲作用等原因造成的。
稳压器内部气相和液相区域温度直接影响着稳压空间液相的蒸发和蒸汽的冷凝,从而对系统压力产生重要影响。图7为稳压器不同区域内温度随时间的变化。
在30%功率稳定阶段,稳压器内温度的分布保持稳定,且存在一定的温差。在功率从30%提升至100%阶段,稳压器下部液相区域温度提升的速率明显大于稳压器混合相区域,这主要由不同的传热机理所造成。稳压器下部液相区域温度的变化主要是堆芯出口温度对流传热迁移引起的;稳压器混合相空间温度变化主要是通过与稳压器下部液相区域的热传导以及混合相空间内微弱的自然对流引起的,热量传递效率远小于前者,从而稳压器下部液相区域温度提升的速率明显大于稳压空间液相区。在功率保持100%稳定阶段,稳压器内温度持续升高,最终稳定在最大值。由于考虑了稳压器外壁的散热,稳压器在竖直方向由下到上温度逐渐减小,存在温度梯度。
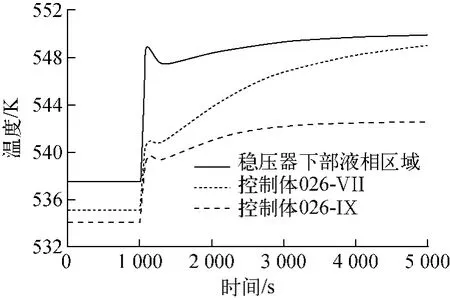
图7 稳压器不同区域温度Fig.7 Temperature in different regions of pressurizer
(2)系统压力变化特性及压力跟随滞后现象
图8为功率调节过程中系统压力的变化。当系统功率增大到100%后,系统压力仍会不断上升,但增加速率减缓,直到压力稳定,且最终的稳定值即为系统压力的最大值。
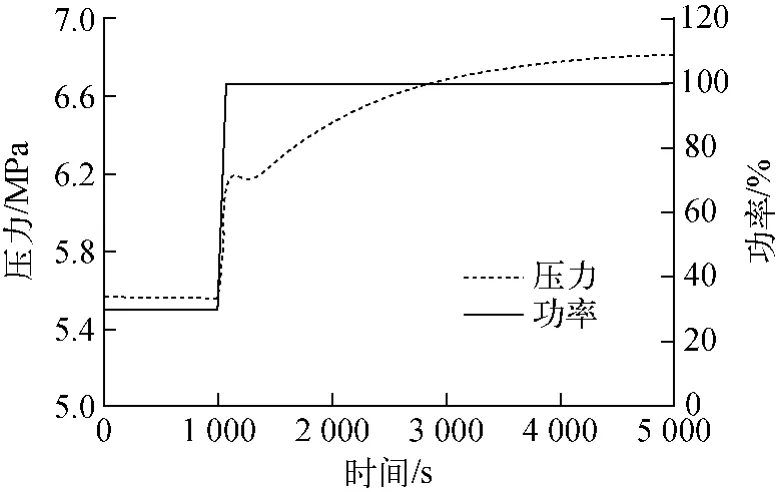
图8 整个动态过程系统压力变化Fig.8 Pressure change in whole progress
系统压力在初始的1 000s内达到稳定值,约为5.56MPa;从1 000s开始,系统压力随功率的提升不断增大,最终稳定值(亦为最大值)约为6.85MPa。整个过程压力增加1.29 MPa,压力增加速率为0.000 19 MPa/s。在功率提升阶段(1 000~1 060s),压力从5.56 MPa上升至6.08MPa,占整个调节过程压力增加值的40.4%;压力增长的平均速率为0.009 9MPa/s,此时压力增加速率远大于整个调节过程的变化速率。这表明压力的增加大部分是在恒定功率(100%)下完成,并非在压力提升过程(1 000~1 060s)完成,压力的变化整体滞后于功率的提升。
为进一步研究系统压力动态变化特性,选定功率提升过程进行分析。选定考察时间范围为980~1 100s,此过程包含功率提升阶段(1 000~1 060s)。在选定阶段,压力变化的斜率逐渐增加,并定义:在功率提升阶段,小于平均压力变化斜率20%的阶段为压力变化滞后阶段。
根据压力变化滞后的定义,压力变化滞后现象出现在功率提升的初始13s(1 000~1 013s),此阶段功率从30%增加到45%,系统压力变化速率约为整个过程平均速率的20%,系统压力从5.56 MPa增加到5.58 MPa,压力增加值仅占整个功率调节阶段压力增加值的3.25%;紧随压力变化滞后阶段,功率增加到100%,压力变化斜率增大,压力会随着功率的增加而近线性增大,此时系统压力变化的跟随性较好,认为是压力近线性跟随阶段(1 014~1 060s);下一阶段功率保持100%不变,压力不断增加但增加率逐渐减小,此阶段被定义为功率提升后压力跟随阶段,如图9所示。

图9 选定阶段系统压力和功率变化Fig.9 Change of pressure and power in selected stage
根据对系统压力变化各影响因素分析,将系统压力变化的三阶段(压力变化滞后阶段、压力近线性跟随阶段、功率调节后压力跟随阶段)划分为4个过程:
第1 过程t1:功率从30%提升至45%,NHR-Ⅱ系统稳压器下部液相体积变化很小,同时加热段出口温度尚未迁移到稳压空间底部液相区域,稳压空间内温度基本保持不变,从而系统压力基本保持不变。此过程持续13s,对应压力变化滞后阶段(1 000~1 013s)。
第2 过 程t2:功 率 从45% 线 性 增 加 到100%,主回路液相持续被加热,平均温度升高,涌入稳压空间的液相体积逐步变大并达到最大值。稳压空间底部液相区域温度从537.5K 增加到544.6K,稳压空间的温度也增加4K。此过程系统压力近线性增加,对应压力近线性跟随阶段(1 014~1 060s)。
第3过程t3:此时功率稳定在100%,涌入稳压空间的液相总量逐步减小,即有液相从稳压器内涌出,主要归因于二回路的冷却增强和压缩反冲作用。同时,稳压空间的温度快速增加。此过程系统压力持续增加,但增加速率明显低于第2过程。
第4过程t4:此过程功率恒定,整个系统稳压液相区域的温度分布稳定,无液相涌入或涌出稳压空间。同时,在稳压器中存在热传导和微弱的自然对流,稳压空间的温度缓慢增加。此过程整个系统的压力仍增加并最终趋于稳定,但增加速率较第3过程缓慢。
综上可知,压力变化滞后发生在第1过程,压力近线性跟随阶段发生在第2过程,且第1、2过程属于功率调节阶段;第3、4 过程属于功率调节后压力跟随阶段。
2)系统温度变化特性
(1)温度滞后现象
在功率调节过程中,堆芯出口温度最先变化,且能实时跟随功率提升。堆芯出口温度变化需经上升段传递到稳压空间下部液相区域,此过程称为温度迁移滞后(图10)。
图10中,两条曲线分别代表堆芯出口温度变化和稳压空间下部液相区域温度变化,在时间轴上呈现的是“曲线平移”。平移时间thys可通过下式估算得到:

其中:Lu为上升段长度;vu为上升段平均流速。本例中平移时间约为35s。
系统温度变化除温度迁移滞后外,还存在温度传递滞后,主要发生在稳压器内。在一体化汽-气稳压器中,当热量被传递到稳压器底部液相区域后,需通过热传导和稳压空间微弱的自然对流将热量传递到整个稳压器内,称为温度传递滞后。由于热量的传导速率远小于热量的对流导热,从而在稳压空间内温度的变化远滞后于系统温度的变化。正是由于这两种温度滞后现象共同组成系统温度滞后,影响系统压力的变化。
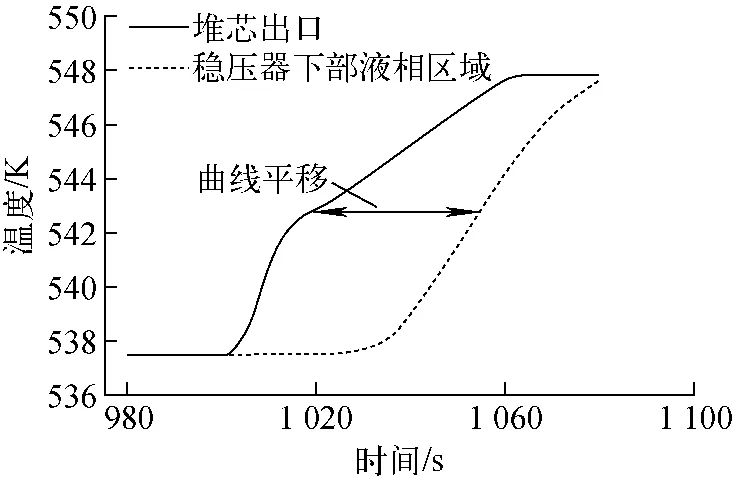
图10 温度迁移滞后Fig.10 Temperature transport hysteresis
(2)堆芯出口过冷度变化
由于压力滞后阶段的存在,影响堆芯出口过冷度变化并威胁系统安全。系统在一定堆芯出口过冷度下运行,堆芯出口温度随功率迅速提升而增加,在压力变化滞后阶段,系统总压保持不变,对应系统饱和温度保持不变,从而造成堆芯出口过冷度大幅减小甚至出现局部沸腾,威胁系统的安全性。图11 为NHR-Ⅱ系统功率快速提升情况下堆芯出口过冷度的变化。堆芯过冷度ΔTc算式为:
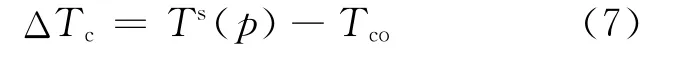
其中:Ts(p)为系统压力下对应饱和温度;Tco为堆芯出口温度。
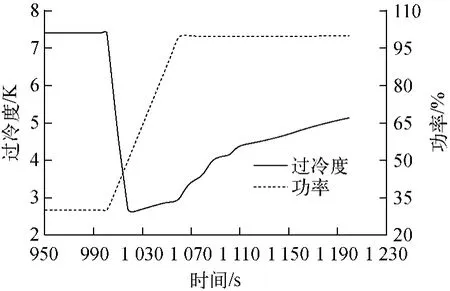
图11 NHR-Ⅱ系统功率快速提升过程堆芯出口过冷度变化Fig.11 Change of core outlet subcooled temperature during power regulation stage
在NHR-Ⅱ系统功率快速提升过程中,堆芯出口过冷度随着功率增加立即减小,在压力滞后阶段从7.3K 减小到最小值2.7K,随后逐步增加。在NHR-Ⅱ系统功率迅速提升过程中,堆芯出口过冷度最小值为2.7 K,表明NHR-Ⅱ系统是安全的。
4 结论
本文研究了一体化汽-气稳压器动态稳压特性,主要结论如下:
1)计算模型能较好地预测一体化汽-气稳压器动态特性,误差控制在可接受范围内,可满足工程应用要求。
2)稳压空间混合相的压缩和稳压器内热量的传递共同决定NHR-Ⅱ系统中压力的变化。这两个因素先后在功率提升过程占主导作用,致使整个调节过程经历压力滞后、压力近线性变化、压力跟随等3个阶段。压力滞后出现在功率调节初始阶段,且此阶段堆芯过冷度会急剧减小。
3)系统温度变化滞后主要是由于系统不同区域传热机理差异引起的,并对系统压力的变化有重要影响。温度迁移滞后主要发生在从堆芯出口到稳压器下部液相区域,由对流传热决定;温度传递滞后主要发生在稳压器内,由稳压器下部液相区域导热和稳压混合相空间微弱的自然对流决定。
4)在功率提升过程中的压力滞后阶段,堆芯出口过冷度迅速下降并达到最小值,可能会威胁整个系统的安全性。在NHR-Ⅱ系统功率突升过程中,堆芯出口过冷度在安全范围内,系统安全。
[1] 张亚军,王秀珍.200 MW 低温供热堆研究进展及产业化发展前景[J].核动力工程,2003,24(2):180-188.ZHANG Yajun,WANG Xiuzhen.Application of the 200MW low temperature nuclear heating rector[J].Nuclear Power Engineering,2003,24(2):180-188(in Chinese).
[2] LEONARD M T.The effect of a non-condensable gas on pressurizer in-surge transientients[R].US: Massachusetts Institute of Technology,1983.
[3] HASSAN Y A,BANERJEC S.Implementation of a non-condensable mode in Relap5/mod3[J].Nuclear Engineering and Design,1996,162:281-300.
[4] AMBROSINI W,FORGIONE N,MANFREDINI A,et al.On various forms of the heat and mass transfer analogy:Diffusion and application to condensation experiments[J].Nuclear Engineering and Design,2006,236:1 013-1 027.
[5] KIM J W,LEE Y G,AHN H K,et al.Condensation heat transfer characteristic in the presence of non-condensable gas on natural convection at high pressure[J].Nuclear Engineering and Design,2009,239:688-698.
[6] KIM T W,KIM J W,PARK G C.Development of non-equilibrium pressurizer model with noncondensable gas[J].Nuclear Engineering and Design,2006,236:375-384.
[7] POLING B E,PRAUSNITZ J M,O’CONNELL J P.The properties of gases and liquids:Ch.11[M].5th ed.New York:WCB/McGraw-Hill,2001.

