基于自然循环回路的非能动安全壳冷却系统数值模拟

黄 政

（中国核电工程有限公司，北京 100840）

非能动安全系统对于提高电站的固有安全性、可靠性和经济性有重要意义，一直是研究的热点之一。在新一代先进核电站的设计中，如AP1000、ESBWR、SMART 等，大多引入了非能动的设计理念［1］。反应堆冷却剂系统发生破口时，会有大量蒸汽进入安全壳空间，使安全壳快速升温升压。若此时喷淋系统因故障或丧失电源而失效，进入安全壳的热量无法导出，则会威胁到作为最后一道安全屏障的安全壳的完整性，造成放射性物质释放到环境的严重后果。

本文针对一种采用自然循环回路的非能动安全壳冷却系统（PCCS），建立自然循环回路的一维均相流模型，研究该系统的稳态运行特性，并对影响系统换热能力的主要参数进行分析。

1 系统组成与运行方式

本文研究的PCCS原理图如图1所示。该系统由6个独立系列组成，每个系列的主要设备包括：2台位于安全壳内的并联换热器，位于安全壳外与大气环境连通的冷却水箱及相关的管道和阀门。

事故发生后，大量蒸汽进入安全壳空间，气体通过冷凝、对流和辐射作用将热量传递给换热器，依靠冷热源密度差和高度差产生的驱动压头克服回路沿程阻力损失，建立并维持工质的循环流动，从而将热量导入作为最终热阱的冷却水箱，使安全壳内的温度和压力降低。当换热器的热流密度较高时，流动工质甚至会达到对应压力的饱和温度而汽化，此时回路上升段及部分加热段将处于气液两相流动状态，而下降段的工质经水箱冷却后重新恢复为单相状态。

图1 PCCS原理图Fig.1 Schematic of PCCS

2 数学模型

2.1 基本假设与节点划分

本文主要研究对象为PCCS自然循环回路和安全壳两部分。为建立自然循环回路均相流数学模型，提出如下假设条件：1）流体为不可压缩；2）仅考虑流体沿垂直管道的一维流动；3）气液两相流速相等，且处于热力学平衡状态，不考虑欠热沸腾；4）能量方程中，忽略气液相界面的黏性耗散及流体动能和势能；5）冷却水箱能保证冷却充分，使下降段入口流体为单相状态；6）相对于安全壳的响应速度，PCCS自然循环瞬态过程可忽略；7）安全壳内气液相之间仅考虑质量和能量交换，不考虑动量交换。

PCCS自然循环回路的坐标系与节点划分如图2所示。仅考虑沿高度z 方向的一维流动，取向上为正，原点位于最低点。回路各段都均匀划分为100个网格节点，并采用交错网格的形式，即压强、焓值及流体物性等参数定义在网格中心，用整数编号表示；而速度则定义在网格边界上，用半整数编号表示。编号顺序与流动方向相同。对于换热器传热管壁面，轴向相应地划分为100段；径向仅考虑2个温度节点。冷却水箱采用1个控制体模拟。

对于安全壳，仅采用1个控制体进行模拟，壳内分别考虑气相空间、液相空间、破口质能释放及PCCS带热作用。

2.2 控制方程

自然循环回路的质量连续性方程为：

图2 PCCS自然循环回路坐标系与节点划分示意图Fig.2 Schematic of coordinate system and nodalization of natural circulation loop of PCCS

自然循环回路的动量方程为：

自然循环回路的能量方程为：

其中：ρ为流体密度，kg／m3；u为流体流速，m／s；p 为压强，Pa；A 为回路管道面积，m2；τw为管道壁面切应力，N／m2；K 为局部阻力系数；f 为摩擦阻力系数；Uw为壁面湿润周长，m；UH为加热周长，m；d为管道直径，m；H 为流体比焓，J／kg；q为换热器传热管的热流密度，W／m2。

通过导热传递的换热器热流量为：

其中：φ 为换热器热流量，W；Tcont和Tf分别为安全壳和流体温度，℃；Tw，in和Tw，out分别为换热器传热管内、外壁面温度，℃；hin和hout分别为传热管内、外侧总换热系数，W／（m2·℃）；dw，in和dw，out分别为传热管内、外径，m；Aw，in和Aw，out分别为传热管内、外侧换热面积，m2；λ 为传热管壁面的导热系数，W／（m·℃）。

冷却水箱的能量方程为：

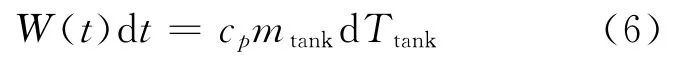
其中：W（t）为t时刻冷却水箱吸收的热功率，W；cp为比定压热容，J／（kg·℃）；mtank为冷却水箱内的冷却水质量，kg；Ttank为冷却水箱内的冷却水温度，℃。

安全壳的质量方程为：

安全壳的能量方程为：

其中：˙mvap和˙mliq分别为进入气相空间和液相空间的净质量流量；˙mbrck，v和˙mbrck，l分别为从反应 堆冷却剂回路破口进入安全壳气相空间和液相空间的质量流量；˙mevap、˙mboil和˙mcond分别为蒸发、沸腾和冷凝质量流量；Wvap和Wliq分别为进入气相空间和液相空间的净能量流量；Wbrck，v和Wbrck，l分别为从反应堆冷却剂回路破口进入安全壳气相空间和液相空间的流体能量流量；Wevap、Wboil、Wcond和Wconv分别为蒸发、沸腾、冷凝和对流的能量流量；Wpccs为PCCS系统的换热功率。

2.3 结构关系式

对于层流（Re＜2 000），f 的表达式为：

对于湍流（Re＞5 000），f 采用Colebrook-White公式［2］计算：

其中：e为管道壁面粗糙度，m；Re为流体雷诺数。

对于过渡区域（2 000≤Re≤5 000），则采用lg f-lg Re的线性插值的方法计算f。

对于换热器传热管壁内外侧的换热系数，内侧采用Churchill公式［3］为：

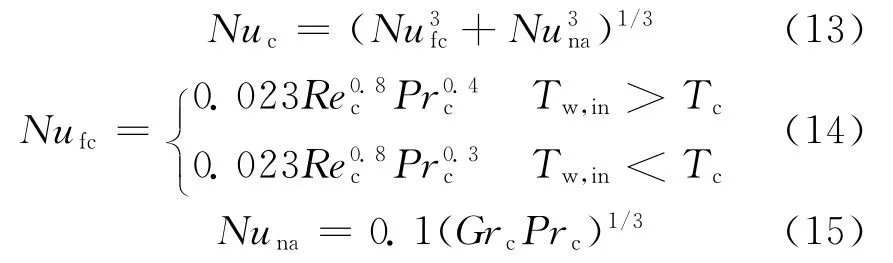
其中：Nuc为传热管外侧冷却剂流体的努赛尔数；Nufc和Nuna分别为强迫循环和自然循环对流换热的努赛尔数；Prc、Rec和Grc分别为冷却剂流体的普朗特数、雷诺数和格拉晓夫数。

对于传热管外侧，主要传热机理为蒸汽在含有不可凝气体条件下的冷凝，则采用Dehbi公式进行计算：

其中：L 为传热管长度，m；p 为混合气体压力，atm；w 为不可凝气体质量分数；T∞为混合气体主体温度，℃。

对于流体物性，单相情形参照IAPWS IF97计算。以下给出两相情形汽水混合物物性计算表达式。

比容为：

动力黏度为：

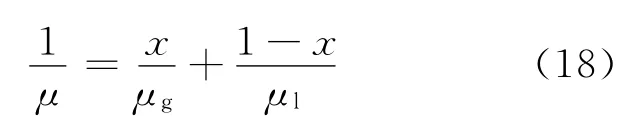
气液混合物焓值：

其中：ν为气液混合物比容，m3／kg；x 为静态含汽率；μ 为气液混合物动力黏度，Pa·s；下标g和l分别表示饱和蒸汽和饱和水。

2.4 数值求解

对于自然循环回路，采用控制容积法在编号i和i-1相邻控制体间积分，对方程进行离散。求解时，先假定一个初始质量流量，从下降段入口开始计算，采用牛顿迭代法进行求解，即令：

其中：上标（n）表示第n步迭代；f（˙m）为构造的关于质量流量˙m 的函数；p′tank、ptank分别为目标换热水箱及实际水箱的压力，MPa。

对于安全壳，可以把上述方程整理成以气相温度和液相温度为自变量的能量守恒方程，再采用二阶牛顿迭代法进行求解：

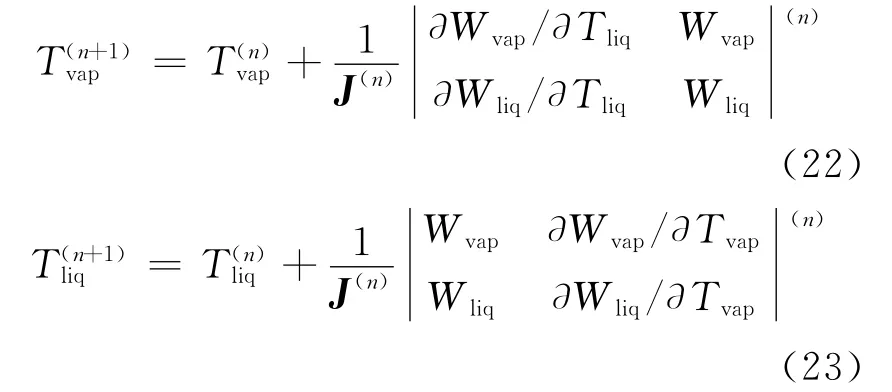
其中，J 为相应的二阶Jacobi矩阵。

2.5 系统参数和边界条件

PCCS回路几何参数列于表1。仅考虑换热器与安全壳的换热，上升段和下降段均假设为绝热边界条件。冷却水箱与大气连通，压力为0.10 MPa。

表1 自然循环回路几何参数Table 1 Geometric parameters of PCCS loop

3 计算结果与讨论

3.1 稳态运行特性

为研究不同冷热源温度边界条件下的PCCS的工作特性，取安全壳温度变化范围为120～150℃，冷却水箱温度变化范围为40～100℃。

图3为PCCS回路上升段出口处的静态含汽率。结果表明，在不同的冷热源温度边界条件下，PCCS可能工作在单相或两相流动状态下。随冷热源温度的升高，工作方式逐渐由单相流动转变为两相流动，且上升段出口静态含汽率也相应逐渐升高，最大值约为0.035。

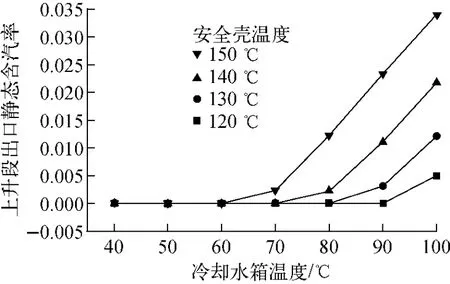
图3 回路上升段出口静态含汽率Fig.3 Static quality at outlet of riser for PCCS

图4为自然循环回路稳态质量流量。可看出，安全壳温度越高，循环流量越大。单相自然循环流动时，流量随冷却水箱温度的升高而减小；进入两相自然循环流动时，流量随冷却水箱温度的升高而增大。因此，在发生相变的过渡点附近，温度区域对应的是循环流量的最小值。

图4 自然循环回路稳态质量流量Fig.4 Steady-state mass flow rate of natural circulation loop

图5为不同冷热源温度下PCCS总的稳态换热功率。可看出：换热功率随水箱温度降低线性减小，随安全壳温度升高线性增加。但在流动由单相向两相过渡转变时，换热功率会有一阶跃变化，使相同冷热源温度下两相的功率高于单相线性外推的功率。这主要是由于进入两相流动后质量流量随冷热源温度的升高而增大造成的（图4）。

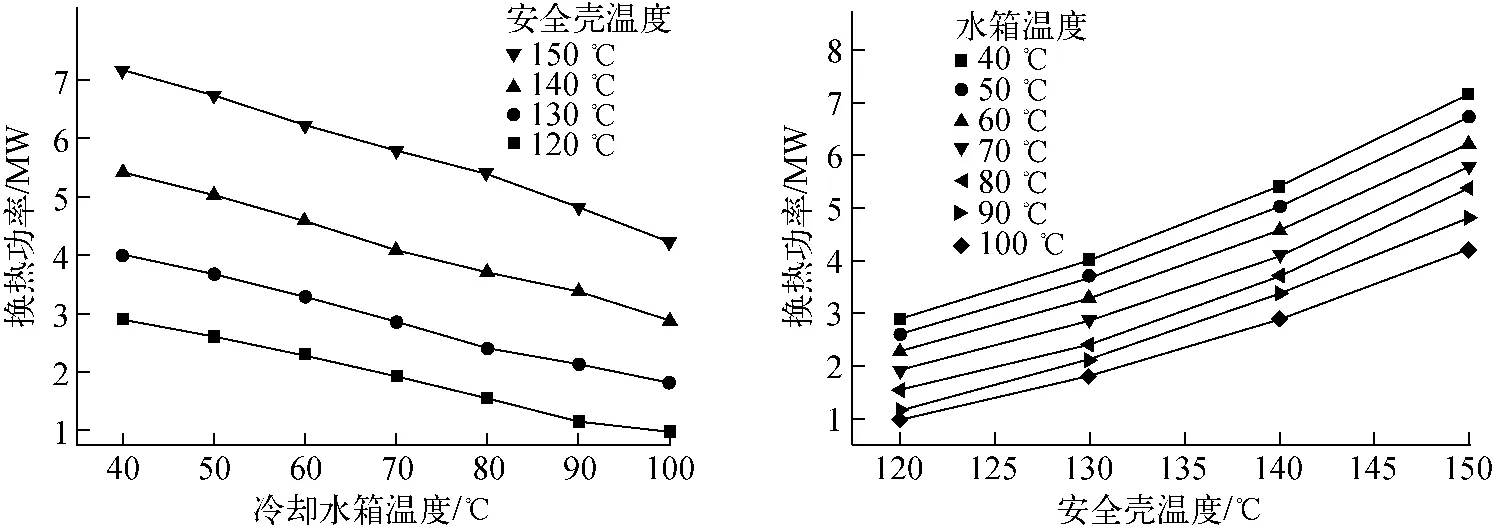
图5 PCCS稳态换热功率Fig.5 Steady-state heat transfer power of PCCS

图6 上升段和下降段最大流速Fig.6 Max fluid velocity of riser and downcomer

图6为上升段和下降段的最大流速。可看出，单相循环时，最大流速变化均不明显（略微下降）；进入两相后均有所增加，且上升段的最大流速变化更为显著。单相循环时，下降段的最大流速大于上升段；而进入两相循环后则相反。整个计算温度范围内，上升段和下降段的最大流速均出现在安全壳和水箱温度最高的工况下（Tcont=150 ℃，Ttank=100 ℃），分 别 为34.1m／s和1.51m／s。

图7为安全壳温度为150 ℃、水箱温度取4个典型值下的回路节点温度和密度分布，其中节点从下降段入口开始编号。对于温度，下降段基本不变；换热器段大致为线性升高；上升段内单相情形保持不变，发生闪蒸后则线性降低。对于密度，单相阶段差别不大，进入两相区域后随含汽率的升高下降明显。图8为不同安全壳和冷却水箱温度下的PCCS回路闪蒸起始点的高度位置。可看出，安全壳和水箱温度越高，发生闪蒸的位置越低，两相段越长。最低位置为4.98m，位于换热器出口位置。

3.2 瞬态运行特性

图7 PCCS回路节点参数分布Fig.7 Fluid parameters of PCCS loop

计算瞬态时，PCCS 共有6 个系列投入运行。通过反应堆冷却系统破口进入安全壳的质能释放数据采用冷管道双端断裂事故，安全壳和PCCS 冷却水箱初始温度为40 ℃，容积1 000m3。计算得到的安全壳和PCCS系统响应如图9～11所示。可看出，PCCS投入早期，由于水箱温度低，安全壳温度高，PCCS换热功率较高，能使安全壳快速降温。随着水箱中的冷却水温度的升高并最终达到饱和沸腾，PCCS功率又逐渐降低，但由于此时衰变热功率亦降低，因此，安全壳温度变化缓慢并趋于稳定。单相阶段，PCCS循环流量较为稳定；进入两相阶段后，流量随含汽率的升高而上升。

图8 PCCS回路闪蒸起始点高度Fig.8 Elevation of onset of flashing for PCCS loop

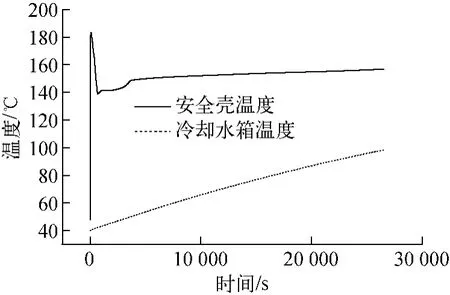
图9 安全壳和PCCS水箱温度Fig.9 Temperatures of containment and PCCS tank

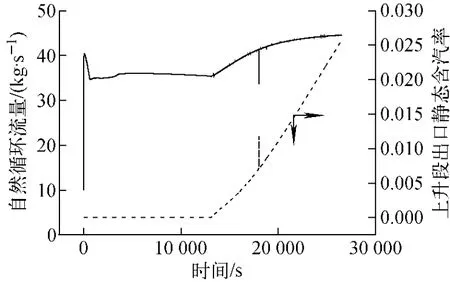
图10 PCCS自然循环流量和上升段出口静态含汽率Fig.10 Mass flow rate of natural circulation and static quality at outlet of riser for PCCS

图11 PCCS换热功率Fig.11 Heat removal power of PCCS

4 结论

本文通过建立数学模型，研究了PCCS的稳态运行特性和回路参数分布情况，以及事故条件下PCCS和安全壳的瞬态响应，得到如下结论。

1）PCCS在不同边界温度条件下处于单相或两相自然循环。换热功率对于安全壳和换热水箱温度近似呈线性分布。

2）安全壳温度越高，循环流量越大。在发生相变的过渡点附近循环流量最小。

3）单相循环时，下降段的最大流速大于上升段；而进入两相循环后则相反。上升段和下降段的最大流速均出现在安全壳和水箱温度最高的工况下。

4）PCCS能在喷淋系统故障的事故条件下，在一定时间内以非能动方式实现安全壳降温。长期阶段换热能力降低，需对水箱进行冷却和补水操作。

［1］ RAO N M，SEKHAR C C，MAITI B，et al.Steady-state performance of a two-phase natural circulation loop［J］.Int J Heat Mass Transfer，2006，33（8）：1 042-1 052.

［2］ BLEVINS R D.Conversion of the Darcy-Weisbach form to the Fanning form used in MELCOR［M］.New York：Krieger Pub Co.，1984.

［3］ DEHBI A，GUENTAY S.A model for the performance of a vertical tube condenser in the presence of noncondensable gases［J］.Nuclear Engineering and Design，1997，177（1-3）：41-52.