含STATCOM的不同阻尼控制器对次同步振荡抑制的影响

，，

(西南交通大学电气工程学院，四川 成都 610031)

0 引 言

中国的能源资源非常丰富，但其分配极不均衡，煤炭资源80%集中在西部和北部，水资源80%集中在西南地区。但另一方面，随着中国经济的快速发展，用电负荷急剧增加，尤其是中国的东部经济发达地区，这一现状决定了必须采用大容量、超高压、远距离输电[1]。

串联补偿技术可以明显地提高输电线路的利用率，促进实现上述输电要求，促进经济效益。但是串联补偿会引起发电机轴系与电气系统以一个或多个低于同步频率交换能量而损坏的现象。次同步振荡是一类严重的系统稳定性问题，不但会使系统产生振荡现象，而且极易造成汽轮发电机组的大轴损毁[2]。如何采取有效的措施抑制次同步振荡是电力系统中一项重要的研究内容。

文献[3]采用人工神经网络法对扭振系统的特征值进行实时分析，可用于在线分析SSO；文献[4]采用多变量频域法对次同步振荡进行分析，可反映出发电机dq轴的不对称性；文献[5]采用开环系统频率特性法对汽轮机调节系统的SSO特性进行分析；文献[6]基于模态控制理论，利用特征值法设计SSDC；文献[7]提出了一种基于传递函数的波特图设计SSDC参数的方法；文献[8]提出了与遗传算法相结合的SSDC设计；文献[9]提出了基于H∞控制理论的SSDC，提高了SSDC的在线计算速度，并使其具有一定的鲁棒性。

国内，STATCOM作为一项成熟的技术，主要用于电压调节、无功补偿、提高线路输送能力等方面，但在利用STATCOM抑制次同步振荡方面的研究较少。基于测试信号法，介绍STATCOM装置的基本原理、控制部件和抑制次同步振荡的原理，根据不同滤波器设计对次同步阻尼控制器的抑制效果不同，设计了3种次同步阻尼控制器，其中，提出一种新的控制器设计方法，利用该方法设计了窄带通次同步阻尼控制器。最后利用PSCAD/EMTDC软件在IEEE第一标准模型基础上，对其抑制效果进行了仿真验证。

1 次同步振荡机理

发电机组的轴系在转动时会有一个自身的模态扭振频率ωm，当发电机组受到扰动时将会使系统产生振动，振动将在定子电压上产生频率为ω0-ωm的次同步电压分量和ω0+ωm的超同步电压分量，相应的转速偏移量为Δω=Aωmcosωmt。这两个分量依据电网在相应频率下的阻抗，产生对应频率的电流，从而造成发电机电磁转矩的变化。如果发电机转速偏移量Δω与电磁转矩变化量ΔTe之间的相角差超过90°，则ΔTe会助增初始扰动，即出现负阻尼。一旦该负阻尼超过发电机轴系所提供的机械阻尼，则轴系扭振得以维持甚至发散，从而形成了机械与电气之间的相互激励，此过程即为机电扭振互作用[10]。它是 SSO 的一种主要表现形式，其原理如图 1 所示。

图1 机电扭振互作用的原理示意

具有串联补偿的单机无穷大系统如图2所示。

图2 具有串联补偿的单机无穷大系统

当输电系统采用串联电容补偿时(如图3)，其电气系统的自然谐振频率ωer为

(1)

则相应有电气系统自然振荡频率fer为

(2)

式(2)中，f0为系统同步频率；ω0=2πf0，XC、XL、X″、XT分别为同步频率下串联电容器容抗、线路电抗、发电机次暂态电抗、变压器正序电抗。

2 STATCOM的基本结构

静止同步补偿器STATCOM是一种新型的并联 FACTS装置。其原理如图3所示。STATCOM 是由全控型的电力电子元件组成的桥式变流器来实现动态发出或吸收无功电流的。STATCOM 的主电路由变流器构成，变流器由直流部分和交流部分组成，交流部分通过电抗器并联接入电力系统，直流部分通过储能元件为电流循环提供一条路径。

图3 STATCOM 的原理示意图

STATCOM主要由变流器、断路器等组成的一次系统和检测环节、控制环节、驱动装置、保护电路、检测装置组成的二次电气系统，如图4所示。STATCOM需要采用连接电抗器或变压器并入系统，这是因为STATCOM装置采用了桥式电路。

图4 STATCOM 结构示意图

整个抑制 SSO 的过程：检测 1 环节检测到发电机的旋转角速度信号，通过检测运算电路得到发电机的转速偏差信号Δω，检测 1 环节把锁相环得到的电压同步信号和计算得到的转速偏差信号Δω发送至控制器，同时检测2环节也把测量得到 STATCOM 直流侧的电压信号经过与参考直流侧电压做差后发送至控制器。控制环节根据设定的控制算法对检测环节发送的信号进行处理，在同步信号的共同作用下通过直接电流控制算法得到触发脉冲信号，脉冲信号通过驱动电路控制变流器的门极，从而控制其导通和关断，从而使 STATCOM 输出合适的电流达到抑制SSO的目的。

3 STATCOM抑制次同步方案设计

3.1 STATCOM的抑制次同步振荡的策略概述

FACTS 装置抑制SSO通常是通过附加阻尼控制器来实现的。在抑制SSO的工作中最重要的是次同步阻尼控制器(SSDC)的设计。图5即STATCOM并联到IEEE次同步谐振第一标准测试模型的原理图。研究表明：SSDC设计的不当，FACTS装置不仅不能抑制SSO，而且有可能恶化SSO状态，重则导致系统次同步失稳。控制器的设计包括选取反馈信号选取、滤波器设计、控制方法选取。

图5 STATCOM 抑制次同步振荡原理图

这里采用发电机角速度偏差作为阻尼控制器的反馈信号。滤波器选择选用相频特性比较好的 Butterworth 滤波器。控制方法如图6所示，利用向系统注入补偿电流抑制 SSO。

图6 FACTS抑制次同步谐振的机理分析

图中，ΔId为当系统受到各种大小扰动后，机组定子侧产生的电流波动；ΔIs为由于机电互激，电气系统侧引起的电流增量；Ic为FACTS 装置补偿的电流；ΔTe为总的电流波动ΔI引起的电磁转矩变化量；ΔTm为系统受到扰动后，原动机的机械转矩增量；Δω为发电机转子的角速度偏差。

3.2 控制器SSDC设计

以 IEEE 次同步谐振第一标准测试模型为研究对象，其中，转子轴系6个轴段构成，6个轴段对应转子轴系6个扭振模式，除去一个刚体模式，进行SSO分析的有5个扭振模式，轴系的机械扭振模态频率分别为15.71 Hz、20.21 Hz、25.55 Hz、32.28 Hz、47.45 Hz。其中，模式5对应的串补度低，模态阻尼非常大，一般不会发生SSO。所以在设计阻尼控制器时只用考虑前4个扭振模式。

3.2.1 分模态次同步阻尼控制器

分模态次同步阻尼控制器(SSDC)的框架见图7，它以发电机角速度偏差Δω作为反馈信号，对发电机轴系的4个扭振模式分别设置模态控制通道。

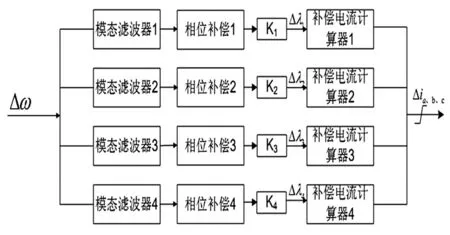
图7 分模态SSDC结构框图

图7中的模态滤波器，下面考虑两种不同滤波器组合对抑制SSO的影响。

第1种：每个模态通道中采用1个模态带通的四阶Butterworth滤波器，记此类型的次同步阻尼控制器为SSDC1。其参数设置如表1至3所示。

表1 SSDC1中滤波器设置

表2 SSDC1 参数设置 /C°

表2中，φ-为次频电流相频响应；φ+为超频电流相频响应；βi为相位补偿角度；γi为可调相位偏差角度。

表3 SSDC1 各模态通道的增益设置

在IEEE第一测试模型中投入SSDC1时系统的电气阻尼特性如图8所示。

图8 投入SSDC1系统的电气阻尼转矩系数

从图8可以看出，投入 SSDC1 时，系统的电气阻尼转矩系数在各个扭振模态频率处为正，但是在两个扭振模态频率之间的部分频率段上电气阻尼转矩系数已经变成负值。为将更多频段上的电气阻尼调节为正，因此设计了 SSDC2。

第2种：每个通道采1个模态带通和其余模态带阻二阶Butterworth滤波器， 每个滤波器的带宽设置为3 Hz，记此类型的次同步阻尼控制器为SSDC2。SSDC2中参数设置如表4至6所示。

表4 SSDC2中滤波器设置/Hz

表5 SSDC2 参数设置/°

表6 SSDC2 各模态通道的增益设置

在IEEE 第一测试模型中投入 SSDC2 时系统电气阻尼特性如图9所示。

由图9对比图8可知，加入 SSDC2 后系统的电气阻尼特性有很大提高，只在24 Hz处电气阻尼系数为负值。

图9 投入SSDC2系统的电气阻尼转矩系数

3.2.2 改进分模态次同步阻尼控制器(SSDC)

为进一步减小次同步阻尼控制器对发电机参数的依赖性，增强控制器的适应性，提出一种新的控制器设计方法：补偿电气谐振频率电流，增加系统在电气谐振频率的互补频率处的电气阻尼。

由图9可知，投入 SSDC2 后，系统只在电气谐振频率的互补频率处电阻尼为负， 而窄带通次同步阻尼控制器只可以增加某一个频率处的电气阻尼，将两者结合，就可以在不影响 SSDC2 为系统提供的电气阻尼情况下，增加电气谐振频率的互补频率处的电气阻尼，实现将整个频段的电气阻尼调整为正。称这种改进型的分模态次同步阻尼控制器为 SSDC3。其基本框架结构如图10所示。

图10 改进分模态次同步阻尼控制器

其第5通道的相位补偿角度和可调相位偏差角度如表7所示。

表7 SSDC3通道5参数设置

表8 SSDC3通道5增益设置

在IEEE 第一测试模型中投入 SSDC3时系统的电气阻尼特性如图11所示。

从图11可以看出，投入将窄带通次同步阻尼控制器与分模态次同步阻尼控制器组合设计新的次同步阻尼控制器SSDC3，所有频段上的电气阻尼均为正值。

图11 投入SSDC3系统的电气阻尼转矩系数

4 STATCOM抑制次同步振荡仿真

为了进一步验证设计的SSDC抑制 SSO 的有效性，利用 PSCAD/EMTDC 电磁暂态仿真软件对图5所示的系统进行时域仿真分析。仿真时忽略转子轴系机械阻尼，设置t=3 s 时处发生三相接地短路，短路持续时间0.05 s。

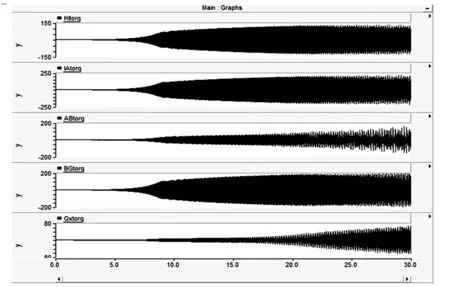
图12 不投入抑制装置时各轴段间的扭矩

从图12可以发现系统在没加 STATCOM 时各个轴段间的扭矩曲线呈现发散趋势，即系统发生次同步振荡。从图13、图14、图15可以发现在投入抑制装置SSDC1、SSDC2、SSDC3后各轴段间的扭矩在故障发生后有小值发散，随着故障的消除，补偿电流注入产生的阻尼作用，扭矩逐渐收敛，最后各轴段稳定在正常扭矩值。由图13和图14、图15相比较可得出，投入SSDC1时，各轴段间的扭矩在7.5 s时收敛为稳态扭矩值，投入SSDC2、SSDC3时，各轴段间的扭矩在6 s左右收敛为稳态值。这是因为投入SSDC1时只有在扭振模态频率处电气阻尼为正值，投入 SSDC2 后除 24 Hz 外整个频段的电气阻尼均为正值。投入SSDC3后整个频段的电气阻尼均为正值，仿真发现系统发生故障后，扭振模态频率处的振荡会引起其他频率的振荡。如果设计的次同步阻尼控制器在整个频率范围内电气阻尼均为正值，其可以在发生次同步振荡时更好更快地加以抑制。

图13 投入抑制装置 SSDC1 时各轴段间的扭矩

图14 投入抑制装置 SSDC2 时各轴段间的扭矩

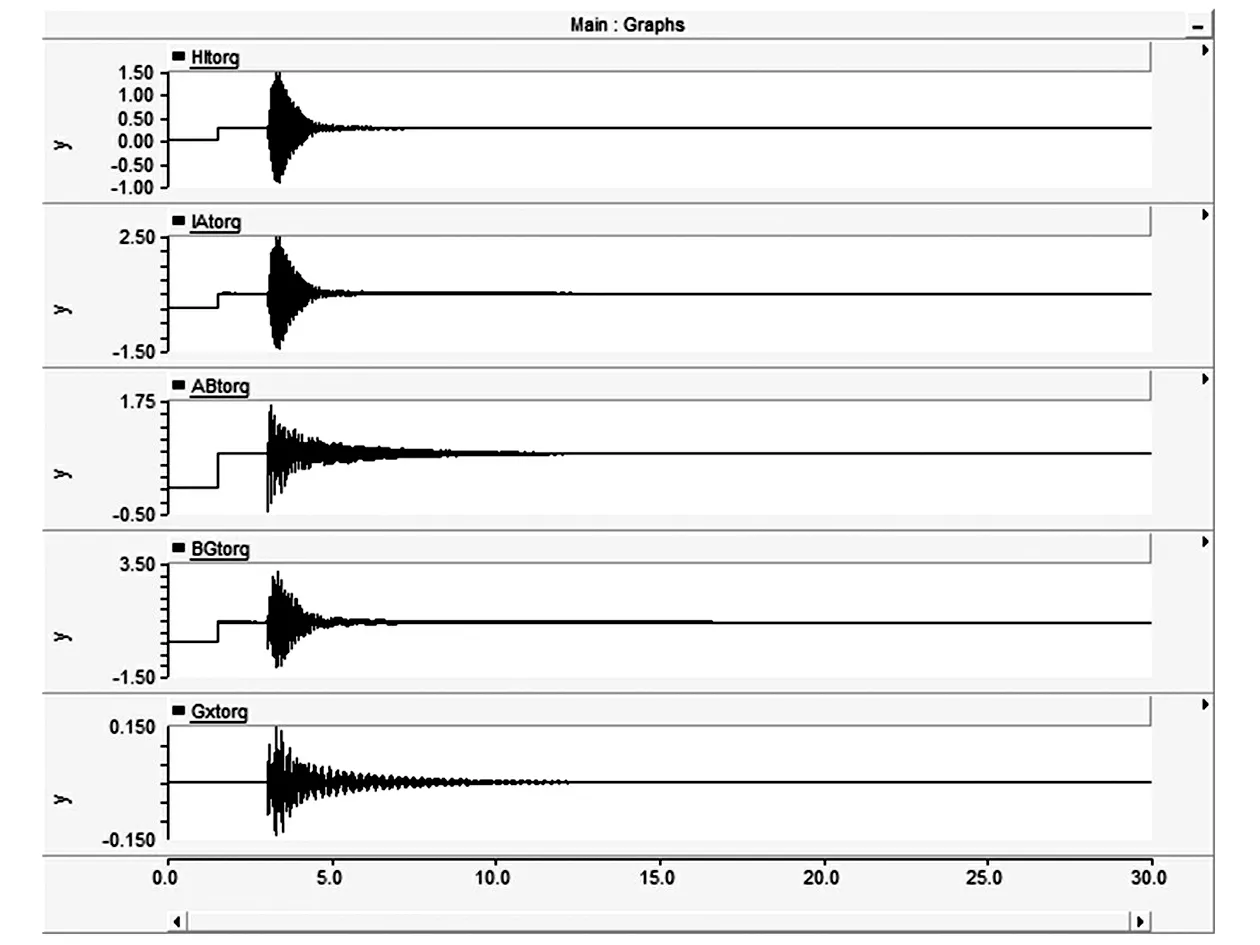
图15 投入抑制装置 SSDC3时各轴段间的扭矩

5 结 论

时域仿真验证与对比，得出下列结论。

(1) 设计的3个次同步阻尼控制器都可以达到抑制SSO的目的， 也就是说在轴系扭振模态频率处电气阻尼转矩系数为正就可以抑制次同步振荡。

(2) 如果可以使整个频段的电气阻尼转矩系数为正，发生次同步振荡后施加抑制装置时发电机各机械量和系统中电气量起始振荡幅值更小，恢复到平衡位置的时间更短，对发电机轴系的疲劳损伤最小，对系统中电气设备的危害也越小。

[1] 张运洲，张卫东．国家电网公司电网“十一五”发展规划综述[N]．国家电网报， 2006-36-38(1).

[2] 周孝信，郭剑波，林集明，等．电力系统可控串联电容补偿[M].北京:科学出版社，2009.

[3]HsuYY，JengIH．AnalysisofTorsionalOscillationsUsingAnartificialNeuRalnetwork[J].IEEETrans．onEC，1992，7(4)：684-690．

[4] 陈陈．多变量频域法分析电力系统次同步振荡[J]．电力系统自动化，1989，(5)：22-27．

[5] 于达仁，徐基豫．大型汽轮机调节系统的设计对轴系扭振的影响[J]．中国电机工程学报．1992，12(4)：35-39．

[6]YY．HsuandL．Wang．ModalControlofanHVDCSystemfortheDampingofSubsynchronousOscillations[J]．IEEProecedings,1989,136(2)：78-86.

[7]R.J.Piwko，E.VLarsen.HVDCsystemcontrolfordampingofsubsynehronousOscillations[J].IEEETranscetionsonPowerApparatusandSystems.1982，101(7)：2203-2211．

[8] 江全元，程时杰，曹一家．基于遗传算法的HVDC附加次同步阻尼控制器的设计[J]．中国电机工程学报，2005(1)：87-91．

[9] 杨秀，王西田，陈陈．基于H∞鲁棒控制理论的高压直流输电系统附加次同步振荡阻尼控制设计[J]．电网技术，2006，30(9)：57-61．

[10]PadiyarKR．AnalysisofSubsynchronousResonanceinPowerSystems[M]．Boston，USA：KluwerAcademicPublishers,1999：87-96.