一道能量转化题引起的思考

（福建省长汀第一中学，福建 长汀 366300）

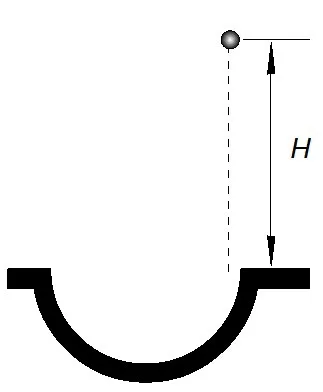
（1）小球第一次离槽上升的高度h；

（2）小球最多能飞出槽外的次数。

解析：（1）小球落至槽底部的整个过程中，由动能定理得

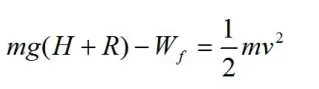
纳入标准：①双上肢麻木、步态不稳和体格检查符合颈椎病，经保守治疗无效的患者；②具有阳性症状和体征，如腱反射亢进、霍夫曼征阳性和四肢感觉麻木、肌力减退等；③C3～C7无节段不稳和后凸畸形的患者。

问题产生在第（2）小题，笔者课前在做这道题时发现，这道题如果用能量守恒定律来做对学生应该显得更容易理解，所以笔者的做法如下所示

两种方法此时得到的结果是一样的，求出来的n一个为6.25，另一个为6.75，因此最终都只能取6次 。有学生提出了疑问——如果此题的数据不是这样的，还是用以上的两种解题方法，则会产生不一样的结果，分析如下：

假设槽半径R=3 m，原题的槽半径R=0.4 m，其它的条件均不变，如果用第一种方法来做，也就是说小球一次都飞不出槽外，但是如果用第二种方法来做的话：

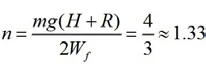
也就是说小球可以飞出槽外一次。显然这里一定是有一种解法是错误的。仔细分析可以发现第二种解法是错误的，这种错误产生的原因是什么呢？

该式的意思是小球从自由下落开始到槽口处（可以是左端的槽口也可以是右端的槽口）重力做的正功与克服摩擦力做的功的代数和满足大于等于0，这样得到n值再去掉后面的小数即为小球在槽中克服摩擦力做功的次数，每一次均为。这个时候小球每完成的机械能的损失，小球就会飞出槽口一次，并且小球在没有完成的累积前，小球的运动方向始终都是沿着圆弧做顺时针的运动，或者是做逆时针的运动，然后才会飞离槽口。这样我们就可以将得到n值再去掉后面的小数来作为小球飞出槽口的次数。

第二个列式，根据能量守恒定律得到

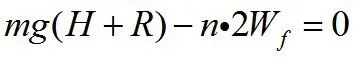
粗看该式，感觉不会有问题，列这个式子的原意是考虑到小球最终会停在是最低点，所以心想就要把这个R也要加进去（正是因为这一步，导至这种做法错误），这样一来每一次经过一次半圆形槽壁，也是损失的机械能为，这样小球可以飞出槽口的次数也就误以为也是这个n值再去掉小数后得到的值。实际上第一次下滑到最低点时的机械能剩下25 J（取最低点为零势能点，此时只有动能），而在这一过程中克服摩擦力做功＝15 J，从最低点开始，小球沿着圆弧还要上升一个R的距离，这一过程需克服重力做功恰好也为m g R＝15 J，这个上升过程还要继续克服摩擦力做功也为15 J，25 J<15 J+15 J＝30 J，显然30 J这个能量是不能让小球出槽口的。也就是说小球还未出槽口就返回又向最低点运动了。

出不了槽口的小球只能在槽内的不断的往复运动，振幅在不断的减小，摩擦力做功是与路径有关的，所以不断的进行累积，直至小球停在最低点。这一过程最终小球的机械能全部转化成了内能，这一过程小球克服摩擦力做功是25 J，这个数值的确是大于=15 J，但是这个25 J中的的前面15 J，并不是在一次的顺时针运动（或者是逆时针运动）连续获得。它是小球通过在槽内不断的往复运动累积而得到，所以此时不能因为E=25 J>＝15 J就认为小球还可以出槽口一次。

总的来看，所以第二种解法错在未认真审题，未仔细研究透整个运动情景，题目要求的是讨论小球有多少次能出槽口，并不是因为物理规律选择错误，若要用第二种解法，正确的解法应该选择槽口为末位置来考虑，而不必去考虑小球是否停下。

根据能量守恒定律

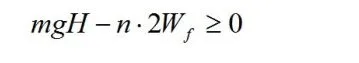
类似这种题型的题目还有很多，不管选用什么物理原理和规律来解题，都要注意选择好所研究的过程，否则极易出现类似的错解。

能量还是贯穿整个物理学的一条主线，从能量角度分析思考问题是研究物理问题的一个重要而普遍的思路曲线运动、竖直平面内的圆周运动等，有变力参与下的运动，一般都要考虑从能的角度帮助分析。在具体的问题面前首先要选好研究对象和研究过程，对象或者是过程的选取（这一步非常重要），可以是用整体法（整过程或整系统），也可以是用隔离法（分成子过程、子系统甚至单个物体），它直接关系到问题能否解决以及解决得否简便，比如求摩擦力做功下物体走过的总路程，用整体法处理就比较简捷。