一种改进的可靠性分配方法及其应用验证*

李大伟，陈云翔，项华春，宋 飞

(1.空军工程大学 装备管理与安全工程学院，西安710051;2.解放军94565 部队73 分队，安徽 蚌埠233000)

1 引 言

可靠性分配是指将系统设计中规定的可靠性指标按照一定的算法分配给各个分系统、部件和元器件，是系统论证、方案设计乃至工程研制阶段的重要工作［1－2］。可靠性分配的科学性对保证指标的实现至关重要。目前，工程上常用的可靠性分配方法有等分配法、比例分配法、AGREE 分配法(考虑重要度和复杂度的分配法)、评分分配法和工程加权法等［3］。等分配法是建立在各个分系统重要度、复杂度等一样的前提下，过于理想化。比例分配法需要找到与该系统非常相似的系统作为参照，不具有一般性。AGREE 分配法、评分分配法和工程加权法虽然考虑到影响系统可靠性的诸多因素，但都不够全面。同时，上述这些方法都是针对串联系统的［4］。

重要度是可靠性分配中一个非常重要的影响因素。故障树是系统可靠性建模的有效工具，传统的故障树分析法计算底事件重要度时需要进行不交化运算。文献［5］给出了一种基于二元决策图(Binary Decision Diagrams，BDD)的方法，文献［6］对这两种方法进行了比较，表明故障树分析法由于要进行不交化运算，计算结果存在误差，BDD 法得到的是精确解。但是BDD 法的计算复杂度与节点顺序有很大关系，文献［7］虽然提出了一种确定最优节点顺序的方法，但是算法复杂度随底事件个数呈指数增长。

贝叶斯网络(Bayesian Network，BN)是进行不确定性概率推理的有效工具，从状态描述和推理机制看，它比故障树分析适用范围更广，非常适用于可靠性分析［8］。基于以上考虑，本文对AGREE 分配法和评分分配法进行了改进，提出了一种综合考虑重要度、复杂度、环境条件、工作时间和技术成熟度的可靠性分配方法，能够实现系统初步设计阶段系统可靠性指标的快速分配。

2 贝叶斯网络的基本理论

贝叶斯网络由Pearl 于1986年提出，是一个包含条件概率表的有向无环图。BN 能表示大规模变量集合的联合概率分布，可以分析大量变量之间的相互关系，利用贝叶斯定理揭示的学习和统计推断功能，实现预测、诊断和聚类等任务［9］。

贝叶斯网由代表变量的节点和连接节点的有向边组成，一个简单的包括6 个节点的贝叶斯网络如图1所示。

图1 简单的贝叶斯网举例Fig.1 Example of a simple Bayesian network

一个具有N 个节点的贝叶斯网络可以用一个二元组N = ＜＜V，E ＞P ＞描述，包括两部分，下面分别介绍。

(1)＜V，E ＞表示一个有向非循环图G。网络图中的节点V={V1，V2，…，VN}(N≥1)表示变量，变量可以是任何问题的抽象。网络图中节点间的有向边E 是弧的集合，表示节点变量之间的关联关系。对于网络图中的有向边(Vi，Vj)，将Vi称为Vj的父节点，Vj称为Vi的子节点。没有父节点的节点称之为根节点，没有子节点的节点称为叶节点。网络图中，用pa(Vi)表示Vi的父节点集合，A(Vi)表示Vi的非后代节点集合。

有向图＜V，E ＞蕴含了非常重要的条件独立性假设，即在给定的pa(Vi)下，Vi与A(Vi)条件独立，即

P(Vi|pa(Vi)，A(Vi))=P(Vi|pa(Vi))

(2)贝叶斯网络图中P 表示一个与每个节点相关的条件概率分布(Conditional Probabilities Distribution，CPD)。由条件独立性假设可知，贝叶斯网络的条件概率分布可表示为P(Vi|pa(Vi))，它代表节点和其父节点的关联关系。当网络图中根节点的先验概率和非根节点条件概率给定时，就可得到包括所有节点的联合概率分布

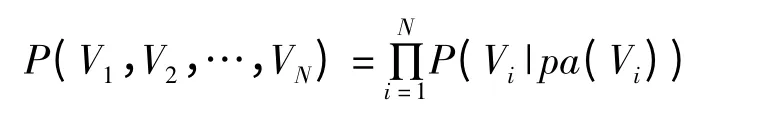
图1中的联合概率分布函数可表示为

当根节点先验概率和节点间条件概率给定时，就可得到任意节点的边缘概率

3 贝叶斯网络的定量分析

由于在BN 中避免了底事件不交化运算，因此计算得到的底事件重要度是精确解。传统故障树(Fault Tree，FT)中最小割集、底事件重要度等运算在BN 中都很容易实现。

3.1 故障树向贝叶斯网络的转化方法

FT 向BN 转化的算法如下:

Step 1:对FT 中的每个底事件，在BN 中建立一个根节点，对该根节点进行命名。对FT 中重复出现的事件，只需用一个节点表示;

Step 2:按照FT 中底事件的失效分布确定BN中对应根节点的先验概率分布;

Step 3:对FT 中的逻辑门，在BN 中建立一个节点，节点状态取值与逻辑门的输出事件一致。FT 的顶事件即为BN 总的输出节点;

Step 4:按照FT 中逻辑门的输入输出关系确定BN 中节点之间的连接关系。

根据以上算法，任何故障树都可以转化为相应的贝叶斯网络图。典型的故障树逻辑门对应的贝叶斯网络及相应的条件概率如图2所示。

图2 典型故障树逻辑门对应的贝叶斯网络Fig.2 Corresponding BN of typical gate for FT

3.2 最小割集求解

在故障树分析中，求解最小割集需先找出所有的割集，然后利用吸收律和等幂律将割集最小化，过程非常复杂，利用BN 求解最小割集则较为容易，求解过程可参见文献［8］。

3.3 底事件重要度计算

底事件重要度表示了底事件对顶事件的贡献，用于改进系统设计、确定需要重点监控的部位和制定故障诊断时的核对清单等。利用BN 中的精确推算法可以求出根节点Ei的重要度。

(1)概率重要度

概率重要度又称Birnbaum 重要度，指在只有第i 个部件由正常状态转为故障状态时使顶事件发生概率的变化。概率重要度度量了部件i 所导致的顶事件发生概率的变化，它并没有直接考虑部件i 实际发生的概率。概率重要度表示如下:

(2)关键重要度

为考虑那些不仅对顶事件的发生起关键作用，自身发生概率也很高或者能够改进的部件，就需要采用一种修正Birnbaum 重要度的重要度计算方法。关键重要度是指部件i 故障概率的变化率与它引起顶事件发生概率的变化率之比，计算公式为

(3)结构重要度

结构重要度表示第i 个部件在系统中所处位置的重要程度，与部件本身的故障概率没有关系，表示为

4 系统可靠性指标分配模型

4.1 可靠性指标分配的原则

(1)重要程度

根据部件的重要程度评定，重要度高的部件分配较高的可靠性指标。由于在系统初步设计阶段底事件的发生概率是未知的，因此，以结构重要度ISti表征部件的重要程度，ISti∈［0，1］。

(2)复杂程度

根据组成系统的部件数量以及组装的难易程度评定，复杂的部件分配较低的可靠性指标。

(3)技术成熟度

根据下属部件的技术水平和成熟度来评定，技术上不成熟的部件分配较低的可靠性指标。

(4)环境条件

根据部件所处的环境评定，工作环境严酷的部件分配较低的可靠性指标。

(5)工作时间

根据部件工作时间来评定，工作时间长的部件分配较低的可靠性指标。

4.2 基于模糊数的底事件评分

在传统的评分分配法中，专家按照10 分制对复杂程度、技术成熟度、环境条件和工作时间进行打分［1］，由于分值范围大，给专家打分带来困难。由于专家的偏好判断和信息的不完全等原因，用模糊数来进行刻画专家打分更符合实际［10］。

考虑到不同专家的专业水平和经验，假设n 个专家的权重分别为λ1，λ2，…，λn，专家对第k 个指标的打分用三角模糊数可表示为珘A1=(l1，m1，u1)，=(l2，m2，u2)，…，=(ln，mn，un)。根据三角模糊数的运算法则［11］，则所有专家的综合打分 珘Ak可用模糊数表示为

4.3 可靠性指标分配建模

在系统可靠性设计中，由于系统组成的复杂性、底事件可靠性指标获取困难，要做到分配结果的绝对精确是不可能的，在初步设计时没有必要浪费大量的时间和精力。因此，在把握总的设计原则的前提下，能满足顶层可靠性指标即可。

(1)基于最小割集的父节点可靠性指标分配

最小割集重要度主要用于系统故障诊断的排序中，每个最小割集代表一个故障模式。按照最小割集重要度一致的思想，将顶层可靠性指标等分:

式中，PT为父节点的可靠性指标，K 为最小割集，m为最小割集数，PK为最小割集分配的可靠性指标。

(2)基于结构重要度和根节点评分的最小割集可靠性指标分配

若最小割集中包含1 阶最小割集，首先将PK在1 阶最小割集之间分配。假设故障树共包含h 个1阶最小割集Ki(i=1，2，…，h)，分别对应根节点Ei，则

式中，PKi表示第i 个1 阶最小割集分配的可靠性指标，Ci为最小割集对应的根节点Ei的综合评分，rij为根节点Ei第j 个因素的评分。

并且满足约束

则根节点Ei分配的可靠性指标PEi为

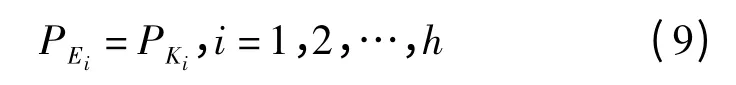
对1 阶以上最小割集，根据可靠性指标分配的原则，将最小割集的可靠性指标向根节点进行分配。假设某最小割集K 共包括n 个根节点Ei(i =1，2，…，n)，则有

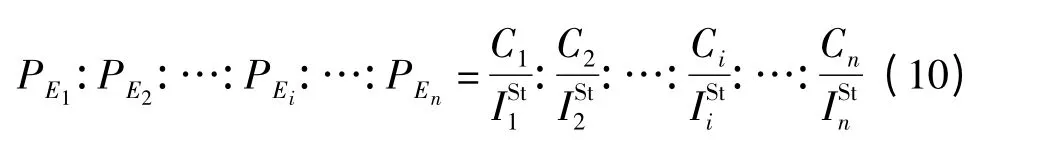
式中，Ci、rij定义同前。

且满足约束

则有

式中，PEik表示由于最小割集中存在交集时PEi的第k 个分配值。

5 案例

以某型飞机横向电传操纵系统“丧失平尾的滚转控制功能”为顶事件构建故障树，以其中部分子树(见图3)为例进行可靠性指标分配。图3中，或门G2、G3 下的底事件是相互独立的。已知顶事件G1“飞控系统控制失效”的可靠性要求为1. 44×10－4，显然，G2 和G3 下包含相同的底事件E1、E4和E5，通过故障树计算时必须进行不交化运算。

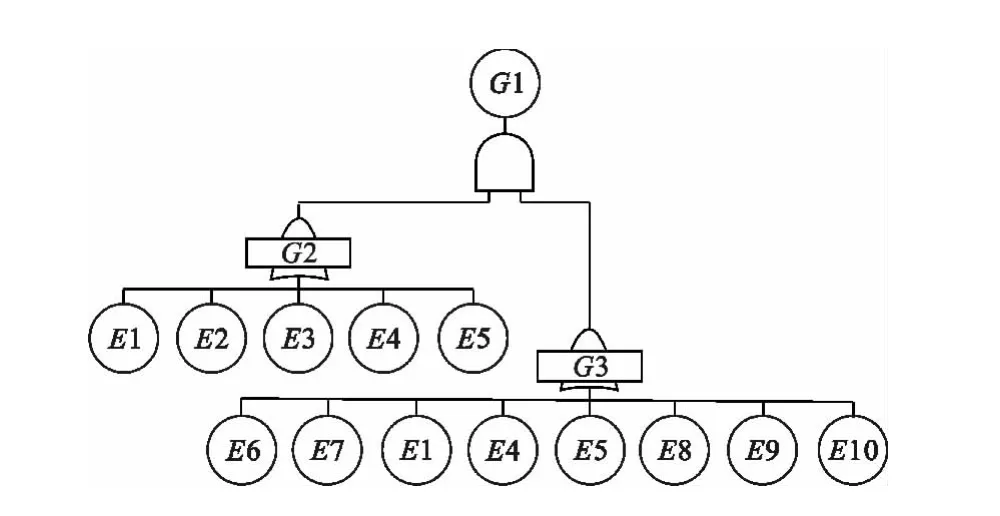
图3 飞行控制系统控制失效的故障树Fig.3 FT of control failure for flight control system

利用Kevin Murphy 等开发的基于Matlab 的贝叶斯网络仿真软件FullBNT［12］，建立了与图3对应的贝叶斯网络，如图4所示。

图4 飞控系统控制失效的贝叶斯网络Fig.3 BN of control failure for flight control system

根据上文提出的基于贝叶斯网络的最小割集计算方法，得到图3所示故障树的最小割集，见表1。

表1 飞控系统控制失效最小割集Table 1 Minimum cut sets of control failure for flight control system

用FullBNT 中联合树推理引擎计算图4中根节点结构重要度，并将计算结果与FTA、BDD 的计算结果进行对比，列于表2。从表2可以看出，利用BN 和BDD 法计算得到的底事件结构重要度是一致的，FTA 得到的结果与上述两种方法存在误差，误差产生的原因是用FTA 求解底事件重要度需进行不交化运算。

表2 结构重要度计算结果Table 2 Results of structure importance

邀请4 位可靠性专家对10 个底事件在复杂度、技术成熟度、环境条件和工作时间方面进行打分，由层次分析法确定4 位决策专家的权重分别为λ1=0.277 5、λ2=0.296 2、λ3=0.220 5、λ4=0.205 8。指标评语与三角模糊数的对应关系见表3。

表3 指标评语与三角模糊数之间的关系Table 3 Relationship between index description and triangular fuzzy numbers

以底事件E1的复杂度评价为例，4 位决策专家的评语分别为一般、一般、复杂、复杂，由式(4)～(5)计算得，E1的复杂度最终评分为r11=6，类似地可以确定其他底事件相应指标的评分，结果列于表4。

表4 专家打分表Table 4 Expert scores

将结构重要度计算结果和专家评分代入公式(6)～(12)对可靠性进行分配并与AGREE 分配法对比，如表5所示。从表5可知，考虑到底事件的综合影响因素后，改进方法对1 阶最小割集对应的底事件中E4、E5的可靠性要求更高，这是由E4、E5的综合评分Ci决定的。1 阶以上最小割集分配的可靠性指标数量级基本一致，但是部分指标进行了重新分配。因此，改进方法分配的可靠性指标能够充分考虑到部件重要度、复杂程度、技术成熟度、环境条件、工作时间对可靠性指标的影响，能满足飞机初步设计阶段可靠性分配要求。

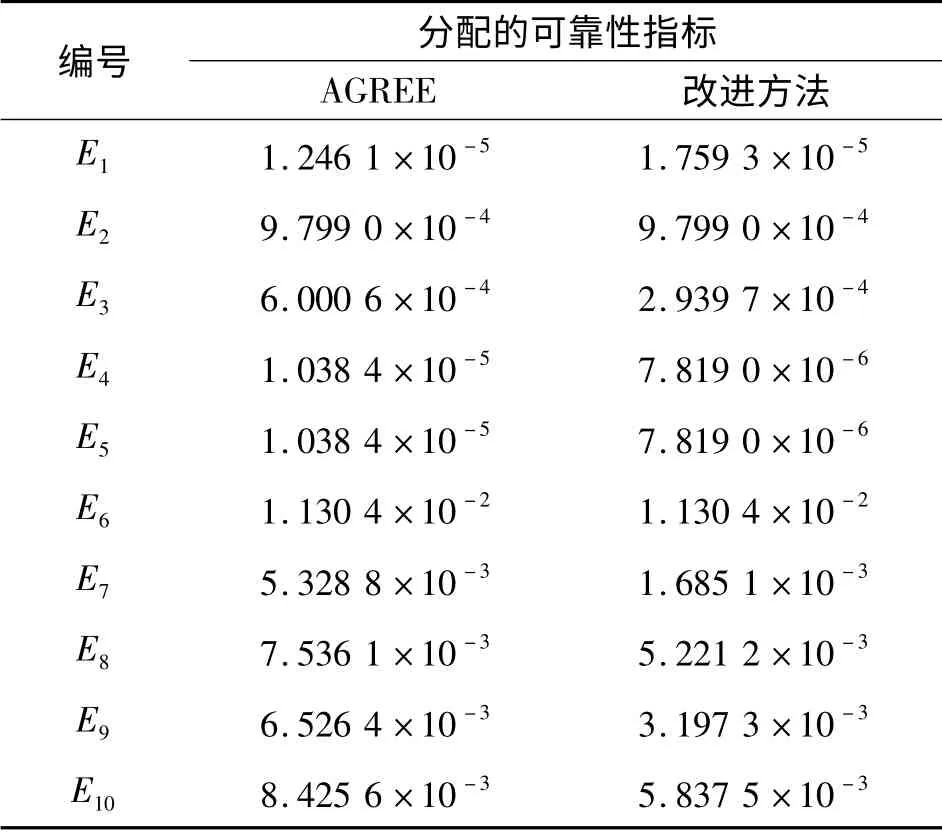
表5 可靠性指标分配结果Table 5 Allocation results of reliability index

6 结 论

(1)通过贝叶斯网络求解最小割集避免了用吸收律和等幂律将割集最小化的过程，计算过程简单。在底事件重要度计算中，贝叶斯网络方法得到的是精确解，且易于计算机编程实现。

(2)所建立的可靠性指标分配模型能够全面考虑割集重要度、底事件重要度、复杂度、环境条件、工作时间和技术成熟度的影响，比AGREE 分配法和评分分配法更为科学。

(3)案例仅给出了与门和或门构成的故障树的可靠性分配，通过将故障树的其他逻辑门转化为基本逻辑门，能够实现复杂系统的可靠性分配，但对于不能转化为与门和或门的逻辑门，该模型还有待进一步完善。

(4)可靠性分配是逐步迭代的过程，本文提出的可靠性性分配模型中底事件重要度按结构重要度计算的，随着设计的深入，在获取底事件实际发生概率的条件下，可以以概率重要度或关键重要度作为底事件重要度进行分配，模型仍然有效。

［1］ 宋笔锋，冯蕴雯，刘晓东，等.飞行器可靠性工程［M］.西安:西北工业大学出版社，2006.SONG Bi－ feng，FENG Yun－ wen，LIU Xiao－ dong，et al. Aircraft Reliability Engineering ［M］. Xi'an:Northwestern Polytechnical University Press，2006. (in Chinese)

［2］ 朱起悦.电子产品研制过程的可靠性管理［J］.电讯技术，2005，45(2):183－186.ZHU Qi－yue.Reliability Management for Developing Electronic Products［J］. Telecommunication Engineering，2005，45(2):183－186.(in Chinese)

［3］ 吴晓颖，张万君.某型引信可靠性分配［J］.四川兵工学报，2010，31(12):38－39.WU Xiao－ ying，ZHANG Wan－ jun. Reliability Allocation for an Fuze［J］.Journal of Sichuan Ordnance，2010，31(12):38－39.(in Chinese)

［4］ 梁晓锋.以顶层参数为目标的舰船可靠性关键技术研究［D］.上海:上海交通大学，2011.LIANG Xiao－feng.Research on Key Technology for Warship Reliability Analysis Aiming at Top－Level Parameters［D］.Shanghai:Shanghai Jiaotong University，2011.(in Chinese)

［5］ Andrews J D，Dunnett S J.Event－tree Analysis Using Binary Decision Diagrams［J］.IEEE Transactions on Reliability，2000，49(2):230－238.

［6］ 于捷，孙立大，石耀霖，等.基于BDD 技术的数控机床故障树重要度分析［J］. 机床与液压，2008，36(12):186－189.YU Jie，SUN Li－ da，SHI Yao－ lin，et al. Analysis of Fault Tree Importance of CNC Machine Tools Based on BDD［J］. Machine Tool ＆ Hydraulics，2008，36(12):186－189.(in Chinese)

［7］ Sinnamon R M，Andrews J D. Improved Accuracy in Quantitative Fault Tree Analysis［J］. Quality and Reliability Engineering International，1997(13):285－292.

［8］ 周忠宝，董豆豆，周经伦.贝叶斯网络在可靠性分析中的应用［J］.系统工程理论与实践，2006(6):95－98.ZHOU Zhong－bao，DONG Dou－dou，ZHOU Jing－lun.Application of Bayesian Networks in Reliability Analysis［J］.Systems Engineering－Theory ＆ Practice，2006(6):95－98.(in Chinese)

［9］ 李海军，马登武，刘霄，等. 贝叶斯网络理论［M］. 北京:国防工业出版社，2009.LI Hai－ jun，MA Deng－ wu，LIU Xiao，et al. Bayesian Network Theory［M］. Beijing:National Defense Industry Press，2009.(in Chinese)

［10］ 刘卫锋，何霞.一种对方案有偏好的三角模糊数多属性决策方法［J］.模糊系统与数学，2013，27(2):155－159.LIU Wei－ feng，HE Xia. A Triangular Fuzzy Number Multi－attribute Decision－making Method with Preference Information on Alternatives［J］.Fuzzy Systems and Mathematics，2013，27(2):155－159.(in Chinese)

［11］ 冉静学.三角模糊数排序方法的研究［J］.中央民族大学学报(自然科学版)，2011，20(4):37－41.RAN Jing－xue.The Research on the Rank of Triangular Fuzzy Numbers［J］.Journal of the Central University for Nationalities(Natural Scientific Edition)，2011，20(4):37－41.(in Chinese)

［12］ Murphy K P.The Bayes net toolbox for matlab［J］.Computing Science and Statistics，2001，33(5):331－351.