基于统计分析的公共自行车服务系统研究

余 敏，张秀英

(郑州铁路职业技术学院，河南 郑州 450052)

0 引言

本文的案例来源于2013 年全国大学生数学建模竞赛的D 题(http://www.mcm.edu.cn/problem/2013/cumcm2013problems.rar)。

公共自行车作为一种低碳、环保、节能、健康的出行方式，正在全国许多城市迅速推广与普及。在公共自行车服务系统中，自行车租赁的站点位置及各站点自行车锁桩和自行车数量的配置，对系统的运行效率与用户的满意度有重要的影响。

附件1［1］为浙江省温州市鹿城区公共自行车管理中心提供的某20 天借车和还车的原始数据，所给站点的地理位置参见附件2［1］。在搞清楚公共自行车服务模式和使用规则的基础上，根据附件提供的数据，建立数学模型，讨论以下问题:

(1)分别统计各站点20 天中每天及累计的借车频次和还车频次，并对所有站点按累计的借车频次和还车频次分别给出它们的排序。

(2)试统计分析每次用车时长的分布情况。

根据公共自行车服务模式和使用规则以及温州市鹿城区公共自行车服务指南［4］，结合实际情况，作出如下假设:

(1)附件1［1］中的数据能够反映该城区公共自行车服务系统的现状;

(2)附件1［1］中借出车站号和还车车站号相同，且用车时长为小于等于1 分钟的记录为无效记录，建立模型时该记录中的数据均不予考虑;

(3)附件1［1］中还车车站号为0 的记录，认为该车丢失或损坏，统计借车频次时有效，而统计还车频次时无效;

(4)每次用车时长不超过24 小时(即1440 分钟)的数据为有效数据;

(5)各站点所提供的自行车型号相同，且每位用车人的车速基本相同，设为12km/h。

根据以上假设，首先对附件1［1］中借车和还车的原始数据进行预处理，把借出车站号与还车车站号相同且用时长小于等于1 分钟的记录以及每次用车时长超过24 小时(即1440 分钟)的记录删除，得到20 天数据的预处理表。

对于问题(1)，利用spss 软件的频数分析和excel 的计算与排序功能，得到:各站点20 天中每天及累计的借车频次和还车频次;按累计的借车频次和还车频次的排序，并根据用车频次和用车时长的分布情况，分析各站点设置是否合理。

对于问题(2)，利用spss 进行频数分析，得到每天的用车时长的分布情况;然后以用车频次最多的一天的数据，建立每次用车时长的分布函数模型。

1 借车频次、还车频次的统计模型的建立与求解

1.1 数据的预处理

由假设2 和假设4 可知，每次用车时长超过24小时(即1440 分钟)以及借出车站号与还车车站号相同且用车时长小于等于1 分钟的记录为无效租车记录，所以要对附件1［1］中借车和还车的原始数据进行预处理。将20 天的数据表导入软件spss，利用spss 软件的数据筛选功能，删除上述两类记录，得到20 天借车与还车数据的预处理表，并将它们导入spss，建立spss 数据文件。

1.2 统计借车频次和还车频次并排序

利用spss 软件，对预处理后的20 个spss 数据文件进行频数分析，计算各个站点每天的借车频次和还车频次，并将20 天各站点的借车频次和还车频次汇总成一个excel 表。然后，利用汇总后的excel 表计算20 天各站点的累计借车频次、累计还车频次、合计用车次数(即累计借车频次与还车频次之和)及每天的总用车次数。最后，再用rank 函数得到按累计借车频次和还车频次的排序结果，如表1 所示(由于数据量过大，这里只列出部分数据及排名)。

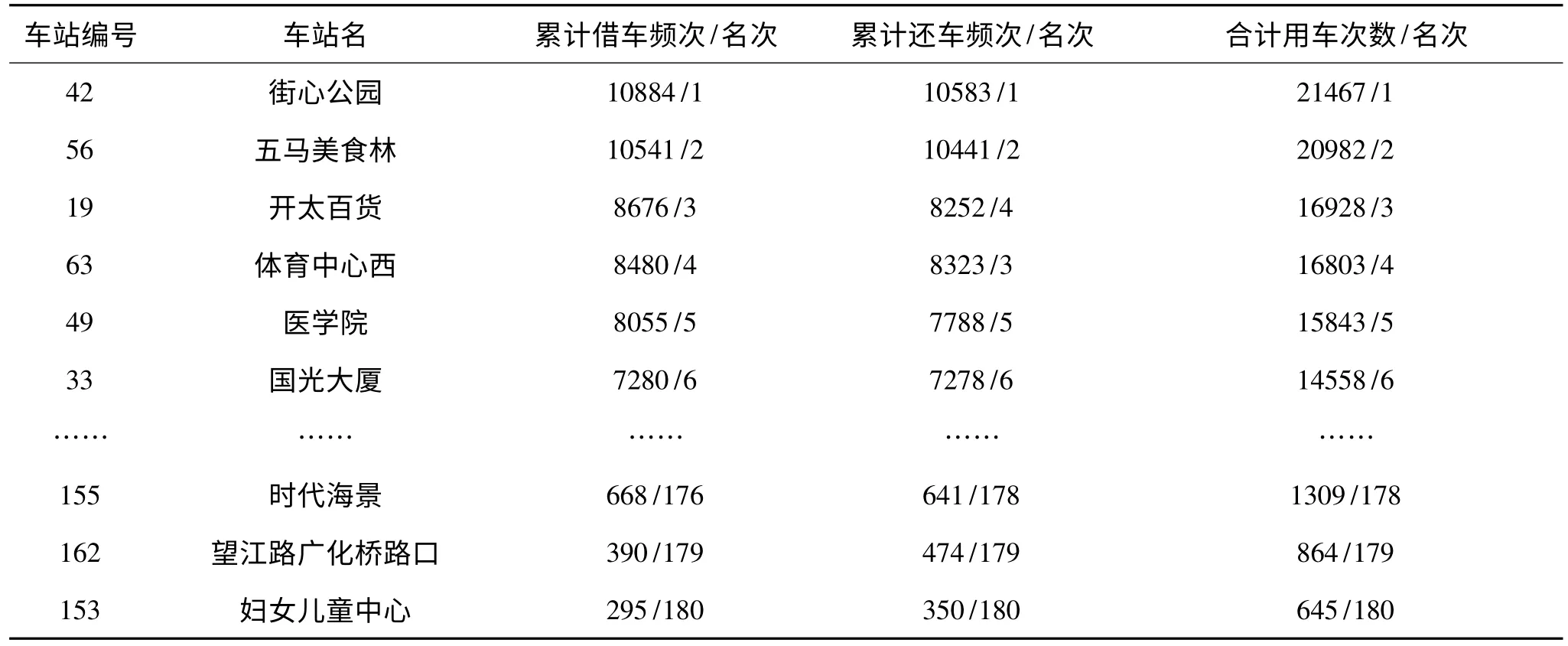
表1 各站点20 天的累计借车频次和累计还车频次及排序

从统计出的每天的借车频次、还车频次及总用车次数可以看出:第13 天的合计使用公共自行车次数为38800，是用车次数最多的一天。

从统计数据还可以看出，各站点每天的借车频次、还车频次和累计借车频次、累计还车频次排名基本一致。如，街心公园、五马美食林的累计借车频次和还车频次排名分别为第1 和第2 位，而且每天的用车次数最多的站点也是这些站;而妇女儿童中心、望江路广化桥路口和时代海景的累计借车频次和还车频次较低，分别排名倒数第1、2 和3 位。结合附件2，可以看出:街心公园和五马美食林附近有较多娱乐场所和办公楼，这些地方的人流密度大，相应的用车人数就会多;而妇女儿童中心、望江路广化桥路口都是郊区位置，附近的娱乐场所和办公楼较少，人流密度小，相应的用车人数就少。这应该是造成在这些车站借、还车频次高和低的原因。结合该区的地图，为了更好地提高自行车服务系统的效益、方便市民出行，可以在街心公园、五马美食林等用车频次较高的站点投放更多的车辆和锁桩或增设新的站点;而在用车频次较少的妇女儿童中心等站点，为了尽可能减少资源浪费，可以适当减少车辆和锁桩数。

2 用车时长分布的模型建立与求解

设样本的观测值为(y1，y2，…，yn)。由统计学知识可知:均值、众数、中位数能反映某变量所有取值的集中趋势和集中位置;样本方差和样本标准差用来刻划样本观测值离散程度;为了更全面地了解数据分布的特点，可以用偏度和峰度来刻画数据的分布形态，其中偏度是描述变量取值分布形态对称性的统计量，其定义为:

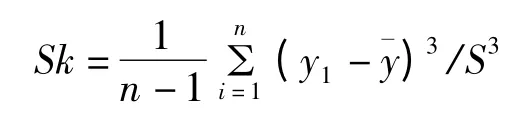
当Sk ＞0 时，分布曲线为正偏态，当Sk ＜0 时，分布曲线为负偏态。峰度是用来描述变量取值分布形态陡缓程度的统计量，其定义为:

当Ku ＞3 时，分布曲线呈尖顶峰度，为尖顶曲线;当Ku ＜3 时，分布曲线呈较平坦曲线。

为了更直观地反映观测数据的分布情况，还可以作出观测变量的直方图、条形图和Q-Q 图，用分布函数进一步刻划变量的分布规律。下面将分别从以上几个方面来研究每次用车时长的分布规律。

2.1 统计分析1～20 天中每次用车时长的分布规律

将预处理后的20 天借车、还车数据表导入spss，用频数分析功能分别计算每天用车时长的均值、众数、中位数、偏度、峰度等，见表2，并作出频数条形图。

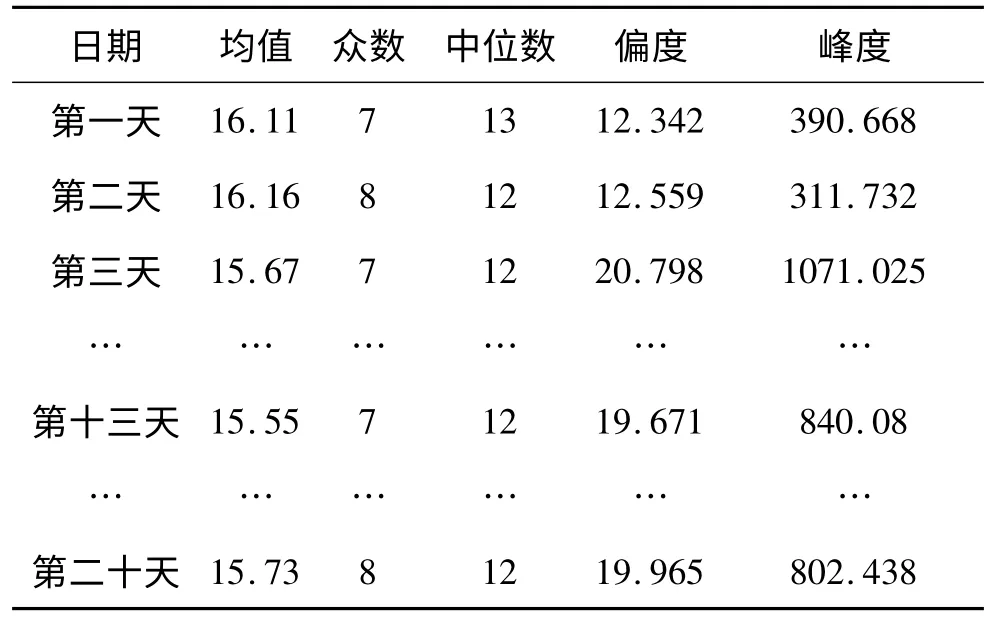
表2 1～20 天每次用车时长的统计

从表2 及每天的用车时长频数表(数据过大，表里略去一部分数据)可以看出，每次用车时长的分布均为偏正态分布，分布曲线均为尖顶曲线，而且大多数天中峰度都远远大于3，说明每天的每次用车时长均不符合正态分布，为正偏态，且从每天的用车时长条形图可以看出:每天用车时长的分布近似于指数分布。每天用车时长的众数均为7～9 分钟，中位数为11～13 分钟，平均数为15～17 分钟，用车时长不超过30 分钟的用车次数均超过85%，用车时长不超过60 分钟的用车次数均超过98%。

下面再以第一天和总用车次数最多的一天(第十三天)为例对用车时长的分布作进一步的分析和研究。

第一天的用车时长分布为正偏态;峰度大于3，分布曲线为尖顶曲线;用车时长的众数为7，说明用车时长较为密集地分布在众数7 的周围。从输出的四分位数可以看出，用车时长为1～7 分钟的占25%，用车时长为1～13 分钟的占50%，用车时长为1～20 分钟的占75%，用车时长不超过60 分钟的占98.8%。图1 为第一天每次用车时长的分布条形图，从图1 可以看出，第一天每次的用车时长分布近似为指数分布。图2 是第一天每次用车时长的正态概率图(Q-Q 图)，图中实线是正态分布的标准线，而散点是实际数据的分布。可以看出偏离正态分布线的点比较多，而用车时长在1～30 分钟之间的点集中在正态线附近，这进一步说明第一天的用车时长不符合正态分布，而是正偏态。作出用车时长在1～30 分钟之间的分布直方图，如图3 所示。

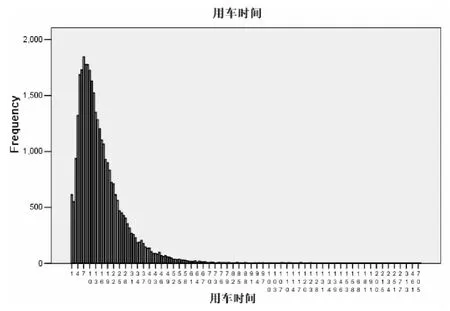
图1 第一天每次用车时长频数的条形图

图2 第一天每次用车时长的Q-Q 图

图3 第一天用车时长在1～30 之间的直方图

2.2 每次用车时长的分布函数模型

为了更好地描述每天用车时长的分布规律，可以将每天的用车时长进行数据分组，以便建立用车时长的分布函数。以第十三天为例，将用车时长每隔10 分钟分一组，统计出每组的频数和频率，如表3。

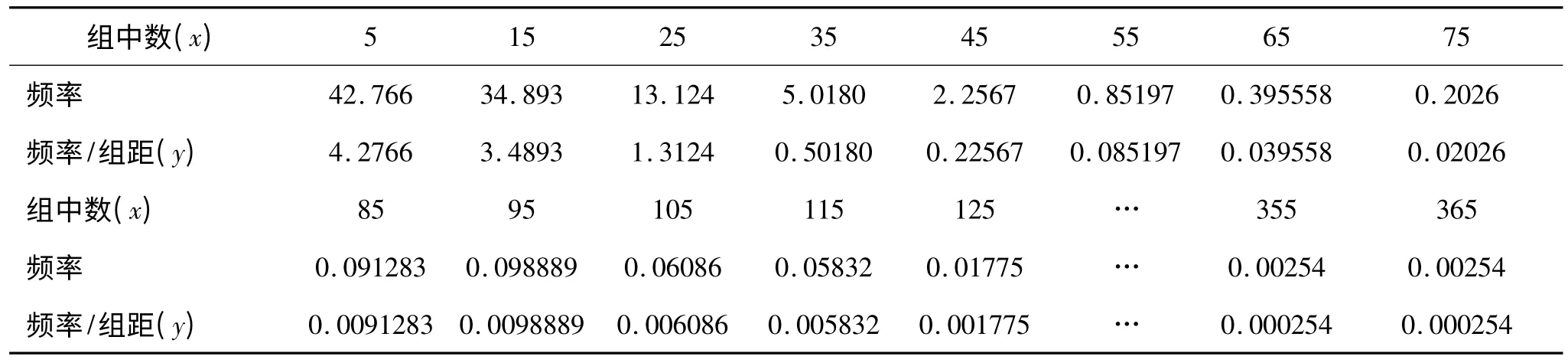
表3 第十三天每次用车时长分组的频数分析表

根据表3 的数据，利用spss 进行曲线回归分析，可以看出，用s 型曲线的拟合效果最好，拟合曲线如图4 所示。

图4 每次用车时长的分布曲线

得到用车时长的曲线回归方程为:

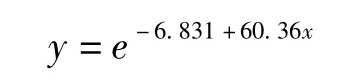
综合以上对用车时长的研究分析，可以看出:用车时长的分布为偏正态，近似为s型曲线;用车时长不超过1 小时的用车次数超过98%，按现行的收费标准，有98%的租车是免费的，这说明目前的收费标准是合理的，有利于推广普及这种绿色环保公共交通系统;平均用车时长为15～17 分钟，如果以公共自行车的平均速度为12km/h 来计算用车距离，可得该区平均用车距离为3～3.4km，这与国内外的调查数据所得的公共自行车的合理用车距离为2～5.5km 是比较吻合的。

［1］全国大学生教学建模组委会D 题:公共自行车服务.http://www.mcm，edu.cn/problem/2013/cumcm2013problems.rar.

［2］章文波，陈红艳.实用数据统计分析及时性SPSS12.0［M］.北京:人民邮电出版社，2009.

［3］李黎辉，陈华，孙小丽.武汉公共自行车租赁点布局规划［J］.城市交通，2009(7):39-44.

［4］李如婷.温州市鹿城区公共自行车服务指南.http://www.wzrb.com.cn/article413173show.html，2013-9-15.

［5］鹿城区公共自行车服务站点列表.http://www.wzcard.com.cn/help/bikeAdress.aspx.