两跳M IMO级联中继网络自由度研究

王寅君，刘 锋，曾连荪

（上海海事大学 信息工程学院，上海 201306）

随着宽带无线技术的发展，人们对移动通信不断提出更高要求，这就需要采用有效的技术手段来提高数据速率、扩大网络覆盖、提高系统容量、增加带宽效率并加强系统在各种环境下的鲁棒性。继续采用传统网络架构将无法适应未来无线应用的要求，为了弥补传统蜂窝网络的不足，设计新的网络结构已经是必然的趋势。在移动基站与终端间采用多天线技术和中继传输成为了实现这个目标的主要技术之一。

多输入多输出（MIMO）[1]技术是利用多根发射天线和多根接收天线进行无线传输的技术，是无线通信智能天线技术领域的重大突破。它可在不增加系统物理带宽的情况下，利用多接口多信道同时进行数据收发，能成倍地提高通信系统容量和频谱利用率，是新一代无线通信系统的关键技术之一。MIMO的一个主要特点是能实现信号在空间上的复用，在高性噪比下，我们使用术语自由度（DoF）来衡量这一空间复用增益。

级联中继技术[2]，以最简单的两跳中继为例，就是指将一个基站-终端链路分割为基站-中继和中继-目的两个链路，从而将一个由于质量较差而中断的链路替换为两个质量较好的级联链路，以获得较高的链路容量以及更好的无线覆盖。基本的中继策略主要有两种，分别是AF（放大转发）、DF（解码转发），其中AF又称为非再生中继方式，而DF解码转发模式又称为再生中继方式。本文主要考虑DF中继策略，在这种模式下，以下行传输为例，中继端将接收来自于基站端的被噪声干扰的信号，同时，它将对其信号进行解码处理，以获得原始信息然后它再对其重新编码并以一定功率发送给用户端。同时，因为解码-转发中继方式具有噪声不会被二次传递的优点，已成为了研究领域中主要考虑的中继转发方式[3]。在实际中继系统中，考虑到中继节点的射频设备的限制，在同一频段上很难做到同时接受和发送信息，一般采用时分双工（TDD）模式，即中继节点用不同的时隙接收和发送信息；或采用频分双工（FDD）模式，即中继节点用不同的频段接收和发送信息。本文主要考虑TDD模式下的DF中继策略。

MIMO技术对多跳无线中继网络容量的影响主要体现在两个方面：第一，MIMO技术通过使用多天线机制，使节点能够同时与多个邻居节点进行并行通信；第二，通过使用多天线增加空间自由度，能够增强空间复用能力，MIMO技术在这两个方面均可提升两跳无线网络的容量。

目前，MIMO两跳无线中继网络容量或自由度问题仍是一个开放性课题[4]，对于MIMO两跳网络的发送、接收天线数不同时的结论仍未给出。文献[5]给出了单向MIMO两跳网络发送、接收天线数相同时的容量上、下界表达式[5]。文献[6]给出了双向MIMO两跳网络容量其发送、接收天线数相同时的容量上、下界表达式[6-7]。

下文将建立典型的MIMO中继网络的模型。着重对发送、接收天线数不同时的情况进行分析，运用改进型的最大割-最小流定理、迫零法[8]得到网络容量与网络自由度的上下界，并证明自由度上界可达。

下文结构如下：第一部分介绍了信道模型。第二部分推导了两跳级联中继模型下的容量与自由度的上界，运用迫零处理推导了自由度的下界。第三部分进行了总结。

1 系统模型

本文所讨论的系统模型如图1所示，该模型包括了3个节点，一个源节点，一个目的节点，一个中继节点。其中源节点有根天线，目的节点有根天线，中继节点的根天线分别用于发送和接收。

由于整个系统工作在TDD模式下，故系统的消息传输分为两个时隙进行（因为不能同时收发）：在第一个时隙内，中继节点接收来自源节点的消息并进行解码处理，此时目的节点不接收消息；在第二个时隙内，中继节点转发处理后的消息给目的节点，此时源节点并不发送消息。在网络的运行过程中，这两个时隙的长度不一定相等，其具体取值情况取决于各跳传输速率的相对大小。

假定所有的信道都是频率平坦的，S-R之间的链路关系为

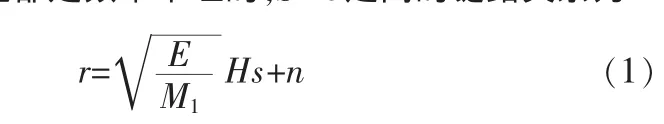
图1 中继网络模型Fig.1 Model of the relay network

其中，r为N×1的接收向量信号，H为源节点至中继节点的链路传输矩阵，其元素为服从N（0，1）、独立同分布的随机变量，即瑞利衰落信道，n为N×1的高斯白噪声，满足公式E{nnH}=IN，发送端的待发消息信号，E为发送节点发射功率。同理R-D之间的链路关系为y=为中继节点至目的节点的链路传输矩阵，也假设为瑞利衰落信道，z是方差为σ2n的高斯白噪声，中继发送端t=[t1，t2…tN]T为N×1的转发信号，P为中继节点发射功率。不失一般性，假设发射功率大小相等（即），下文中统一使用作为发射功率。

2 系统容量与自由度

在本章中，将先推导出上述MIMO两跳TDD网络的容量与自由度上界，然后通过使用迫零处理方法来证明自由度上界是可达的。

2.1 容量与自由度上界分析

最大流-最小割定理给出了网络容量的上界，但其适用于全双工网络。对于半双工网络，需要进行一定改进，以反应网络的多种状态。

如图2所示，系统网络模型工作在TDD模式下，此时链路的每一跳都是下一跳的输入，网络可以看成是由两个无线信道组成的级联信道，即两个单用户的MIMO信道的级联。根据信息论的知识，级联信道的容量小于等于它的每一个子信道的信道容量。如果将源节点至中继节点之间的割集记为Cu1，将中继节点至目的节点之间的割集记为Cu2，那么该网络的容量上界为 min（Cu1，Cu2），Cu1，Cu2可以通过改进的最大流-最小割定理[4]求得。

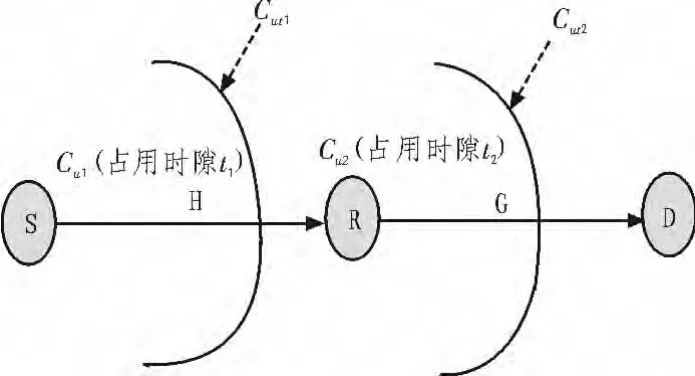
图2 最大流-最小割图Fig.2 Sketch map ofmax-flow min-cutmethod

由于网络分为两个状态运行，第一个状态中第一跳处于激活状态而第二跳为非激活状态，故此时只有一个割集有效，即源节点S与中继节点R之间的割集Cu1=t1I（s；r）；同理，第二个状态中第一跳处于非激活状态而第二跳为激活状态，故此时也只有一个割集有效，即中继节点R与目的节点D之间的割集Cu2=t2I（t；y），此处已经考虑了链路激活的时间。记第一跳链路的容量为C1，第二跳链路的容量为C2，则两个割集简化为

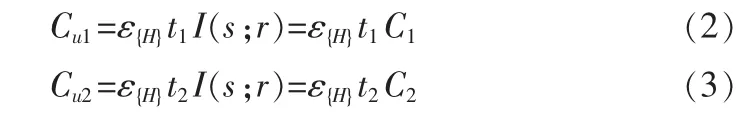
故容量上界可以表示为

对于C1，当s为循环高斯复随机变量时得到容量值最大值[4]，有公式

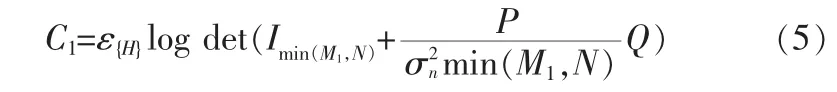
其中 N≥M1时，有 Q=HHH，当 N＜M1时，有 Q=HHH。

同理，可推得：

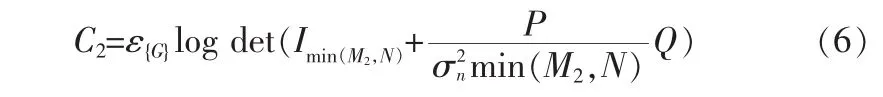
考虑高信噪比的情况，此时信道容量可以简单的表示为

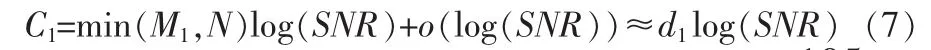
C2=min（M2，N）log（SNR）+o（log（SNR））≈d2log（SNR） （8）

其中SNR为平均信噪比，d1=min（M1，N）为第一跳链路的自由度，d2=min（M2，N）为第二跳链路的自由度。

2.1.2 N≤m的情况

当N≤m时有Q=HHH，同理运用简森不等式可得：Cu1≤t1

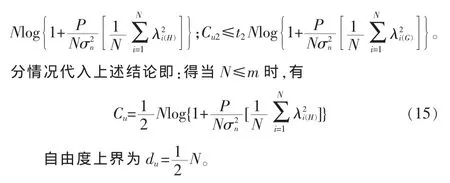
2.1.3 m＜N＜M 的情况

在m＜N＜M时，通过运用简森不等式，且根据最优时隙分配，可得到如下结论：

2.2 自由度下界分析

我们使用线性迫零（ZF）[5]来求解自由度的下界dlower。先简要说明下ZF的原理及优缺点，迫零的译码算法就是找到一个加权矩阵 W，使其满足关系式：WiHj=1（i=j），WiHj=0（i≠j），这里的Wi和Hj分别表示加权矩阵W的第i行与信道矩阵H的第j列（符合该条件的加权矩阵就是H的伪逆矩阵H+）。作为利用信道传输矩阵H+的伪逆矩阵来实现信号分离的一种算法，迫零算法能够消除信号间的干扰，但是却放大了被检测信号的噪声。不过对于自由度来说，线性迫零处理即可获得最大的自由度。

对于迫零法的运用需要注意一点，即迫零法的处理位置，当发送端天线数小于接收端天线数时，在接收端进行迫零检测即可，当发送端天线数大于接收端天线数时，需要在发射端进行迫零预编码。

下界需要讨论的情况与上界相同，包括：1）N≥M，2）N≤m，3）m＜N＜M。

2.2.1 N＞M的情况

当N＞M时，第一跳中中继（接收端）天线数大于源（发送端）天线数，因此我们仅需在中继（接收端）进行ZF检测。通过对接收信号乘以信道伪逆矩阵H+，即可得到式子H+r=s+H+n，从该式可以看出，经过迫零处理后用sˆ恢复了信号s。信道H服从瑞利分布，则其依概率为满秩矩阵，故r（H）=min（M1，N），因此第一跳可用的最大数据流为 min（M1，N）=M1。 在第二跳中中继（发送端）天线数大于目的（接收端）天线数，该情况下需要在发送端进行ZF预编码。由于信道矩阵G服从瑞利分布，且为满秩矩阵，可得第二跳可用的最大数据流为min（M2，N）=M2。 此时需要对两跳传输数据进行速率匹配，这可以采用块衰落模型来实现，即s为一个M1×K的数据块，其中K为M1M2的整数倍。将待发送信号转换为M2个数据流s˜，然后乘以信道伪逆矩阵 G+，得到待转发信号 t=G+˜，经过信道G传输后目的节点得到的信号为

3 结 论

本文中，推导了MIMO中继网络中源节点天线数与目的节点天线数不同时单源-单中继-单宿网络模型的自由度上下界，在上界讨论中，可以发现对网络自由度都有一定的影响，网络3个量的大小关系决定了不同情况下的自由度。在下界情况中，我们选用较为简单但可行的迫零方法来求解下界，得到自由度下界与上界相等的结论。

[1]李方敏，马小林，方艺霖，等.MIMO多跳无线网络[J].软件学报，2010，21（4）:732-749.LI Fang-min，MA Xiao-lin，FANG Yi-lin，et al.MIMO wireless networks with multi-hop[J].Journal of Software，2010，21（4）:732-749.

[2]李光平，杨亮，冯久超，等.两跳MIMO中继系统通信性能分析的研究发展[J].电讯技术，2011，51（8）:154-158.LIGuang-ping，YANG Liang，FENG Jiu-chao，etal.Research progress on performance analysis of two-hop MIMO relay systems[J].Telecommunication Engineering，2011，51 （8）:154-158.

[3]祖立军，王平，王玉金，等.时分半双工MIMO中继系统性能分析[J].计算机工程，2011，37（2）:88-93.ZU Li-jun，WANG Ping，WANG Yu-Jin，et al.Performance analysis of time-division half-duplex MIMO relay system[J].Computer Engineering，2011，37（2）:88-93.

[4]张源，高西奇.三节点无线高斯中继信道容量分析[J].通信学报，2006，27（7）:127-134.ZHANG Yuan，GAO Xi-qi.Capacity analysis of three-node wirelessgaussian relay channel[J].Journalon Communications，2006，27（7）:127-134.

[5]HELMUT Bolcskei，ROHIT U.N，Ozgur Oyman，et al.Capacity scaling laws in MIMO Relay networks[J].IEEE Transactions on Wireless Communications，2006，5 （6）：1433-1444.

[6]VAZE Rahul，HEALTH R W.Capacity scaling for MIMO Two-Way Relaying[C]//Proc of the ISIT，2007:1451-1455.

[7]NIESEN Urs，DIGGAVI S N.The approximate capacity of the gaussian N-relay diamond network[J].IEEE Transactions on the Information Theory，2013，59（2）:259-263.

[8]李美艳.MIMO系统中ZF算法实现[J].信息通信，2011（4）:17-18.LIMei-yan.The implementation of ZF algorithm in MIMO systems[J].Information&Communications，2011（4）:17-18.