以水银为介质的微加速度开关静力学分析

孙宪南,贾建援

（1.陕西广播电视大学，710061;2西安电子科技大学，710126）

1 微开关的发展

自Frobenius在1973年首先制作出一种金属悬臂梁型加速度开关以来，已经出现了各种不同的MEMS加速度开关。在工作原理上可以分为两类：一类是准静态开关，该开关结构是通过弹性结构连接一个质量块，并将质量块作为一个敏感质量和可动电极，当所受的加速度达到一个预定阀值时，质量块受力作用,克服弹性恢复力,发生位移达到一个预设位置,并与一个定电极接触,从而触发电信号,导通电路使开关工作。这种开关对于工艺容差要求严格，精度较低，阈值范围局限在低频低量程加速度范围内，测量能力和环境适应能力较弱，容易造成开关失灵或误操作，难以实现智能化集成。另一类开关是动态开关，这类开关受惯性力,弹性恢复力,应力和静电吸引力等多个力共同作用。加速度阈值通过动态方程计算分析确定，因而这种开关具有动态信号的测量能力。

加速度开关是感受加速度的重要惯性器件,为了满足控制系统的保险功能要求,加速度开关应具备体积小、机械接触可靠、允许通过电流大、精度较高等特点。传统的加速度开关采用精密机械加工,存在体积较大、抗震能力较弱等不足。因此,迫切要求研制新型的微加速度开关。微流体加速度开关是一种受加速度控制的开关量传感器。它可以作为控制开关使用,也可以用来提供开关量信号。随着微机械加工技术在传感器领域中的应用和推广,已经出现了不同类型的微加速度开关,这些开关根据用途的不同而具有不同的结构形式。本文中以水银为介质的微加速度开关，利用在常温下水银是液态金属、表面张力大的特点，构成对加速度敏感的液体电极，水银电极与固定电极组成加速度开关，它的抗载能力不受元件（水银）强度的限制，因此过载量程比可以极大提高。利用水银这种导电液体作为开关通断的介质，具有接触面积达，接触电阻小的特点。因而适用于大电流应用领域。

2 水银加速度开关原理

用水银作为对加速度敏感的弹性电极与硅片上电极构成硅微加速度计，独特之处是用液体弹性电极代替通常的固体弹性电极。其目的是探索一种抗高过载、低量程、高灵敏度、低成本的加速度传感器。这种加速度计具有结构简单、对硅微加工工艺要求低、本征抗高过载、易于集成SOC (system on a chip)、易于实现三维加速度测量的突出优点;对于冲击环境下的惯性测量有不可替代的作用。高性能、低成本、微体积、易于与相关系统集成SOC的微加速度传感系统的应用前景十分广阔。

2.1 结构组成

2.1.1 基板结构

基板为左右对称结构，如图2.1所示。正向加速度阀门开启使水银流动，反向加速度阀门关闭使水银不流动。在硅基板上刻蚀出水银储放腔体、水银微通道和气体微通道，保留通道壁突台和腔体外框突台。水银张力膜将流体区域分隔为水银腔和气体腔，两通道壁所夹下部区域构成水银微通道，腔体外框、通道壁和阀门间的缝隙构成气体微通道。

2.1.2 盖板结构

盖板与基板键合封装，形成矩形储液腔和矩形微通道。在基板/盖板/基板与盖板的水银通道位置制备电极，水银张力膜随加速度的变换发生位移，通过水银的流动使电极导通或断开。

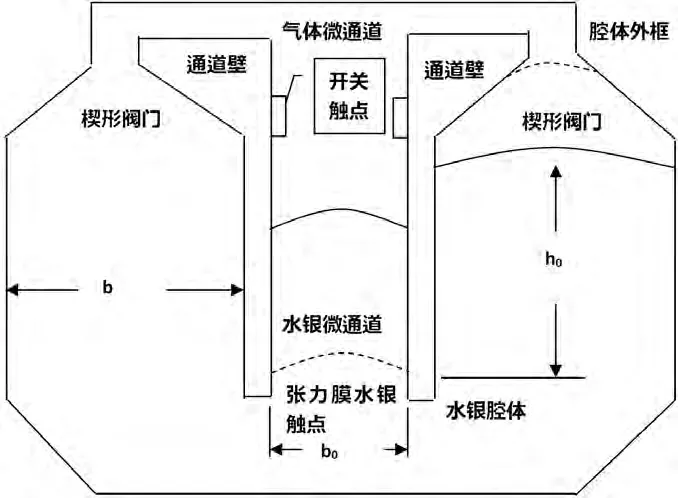
图2.1 加速度开关结构示意图

2.2 工作原理

在载体加速度由10g降低至1g的过程中，开关处于断开过程。首先加速度降至9.9g时，精准的触点结构设计可保证开关在准确的位置断开。然后，在加速度由9.9g降至或低于1g的过程中，出于触点断开、阀门开启状态。当加速度继续降低时，阀门关闭，开关恢复到初始限位状态。

2.3 微尺度效应对微流体的影响

当流道和型腔特征尺寸小于1 mm时，支配流体流动的物理环境及其自身特性发生变化，探明微尺度条件下流体的流动特性对微纳零件的制造与微机械装置控制系统的设计十分重要。因此，随着不同领域对零件微型化要求的不断提高，微流体流动行为的研究已成为微注射成型技术、甚至整个微机械领域的热点之一。

在有关微流体流动行为的研究中，J.Pfahler等。考察了流体在硅材料矩形微流道中的运动特性。实验结果表明：在截面尺寸相对较大的微流道中流体的运动规律与Navier-Stokes方程式相吻合；而当矩形截面流道深度H降至0.8时，试验结果偏离Navier-Stokes方程的计算结果。李勇等以微圆管为对象，研究了用Navier-Stokes方程描述微流体运动特性的适用性。结果表明，对于运动粘度为2.6×10-6m2/s的硅油，当圆管直径降至4.5时，Navier-Stokes方程不再适用；对于管径为11.2的流道，当流体的运动粘度为4.3×10-4m2/s时，流量与压力损失仍呈比例关系。江小宁等研制了一套测量微尺度流动流量的系统，并测量了管径为8，14和24圆管流道内流体流量与压力损失的关系。结果表明，在这样的条件下，流体依然不可压缩连续流动，且实验结果与Navier-Stokes方程式的描述十分接近。在微流体流动过程中，由于微尺度效应作用，表面力作用增强，粘性力远远超过惯性力，流道直径减小导致微流体雷诺数减小，沿程阻力系数增大，且微流道的长径比增大。

3 静力学公式

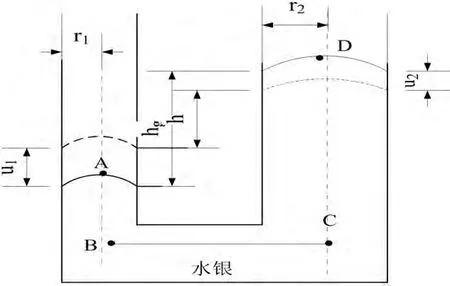
图3.1 圆管道水银液面模型示意图

3.1 静力学模型

如图3.1，曲面为水银液面，r1，r2分别为两微管的半径，h为加速度值为a下的两管水银液面高度差，hg为重力加速度下两管液面高度差，u1，u2分别为加速度a下的两管水银液面运动的位移。

在静止状态下，由于微通道内表面张力的作用，分别为水银微通道和水银腔体之间有一高度差h。根据Yong和Laplace式公式

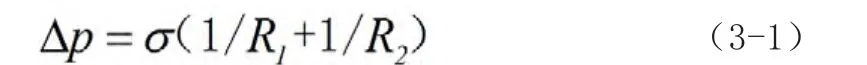
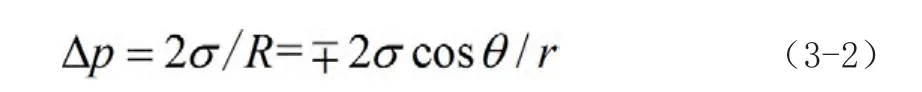
3.2 水银微通道内的静力学方程

由图3.1可看出，B和C点是等压面，即PB=PC，由静止液体静压强公式

因为表面张力的作用，还要考虑附加压强的作用。所以：

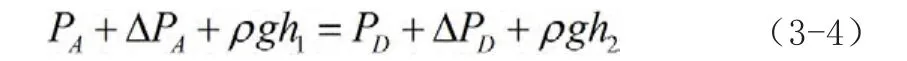
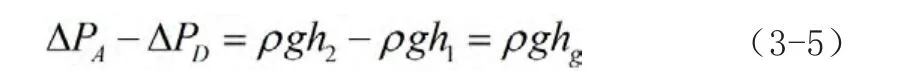
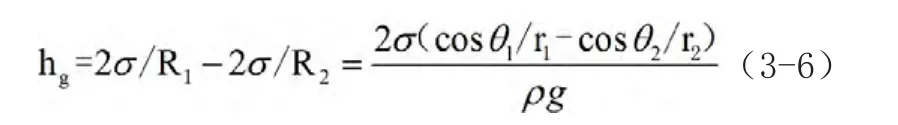
上式为重力加速度下的两管水银液面高度差公式，当加速度变为a时，上式变为：

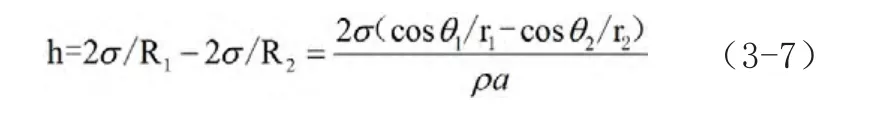
考虑几何约束条件（微管道中水银运动时体积不变），即：

代入式（3-6）和（3-7）得出：

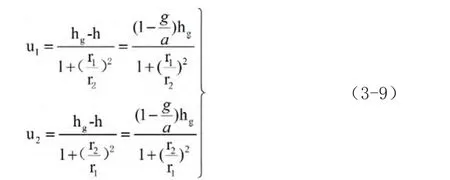
此式即为在加速度a下，两微管中水银液面的位移方程。

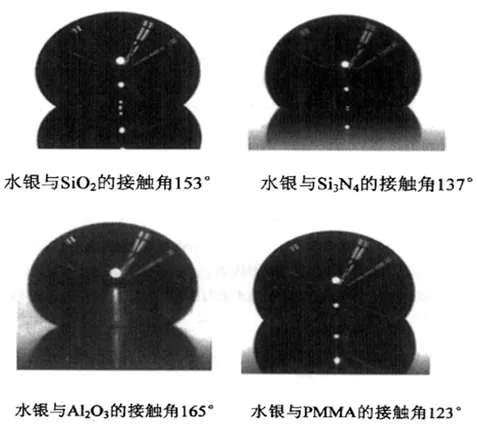
图3.2 水银同四种物质的接触角

式（3-7）中：h为加速度为a时，图4.1两管两液面的高度差，由此看出，接触角和表面确定，水银微通道在加速度a下的上升高度，就能确定。图3.2为朱红试验测出的接触角示意图。

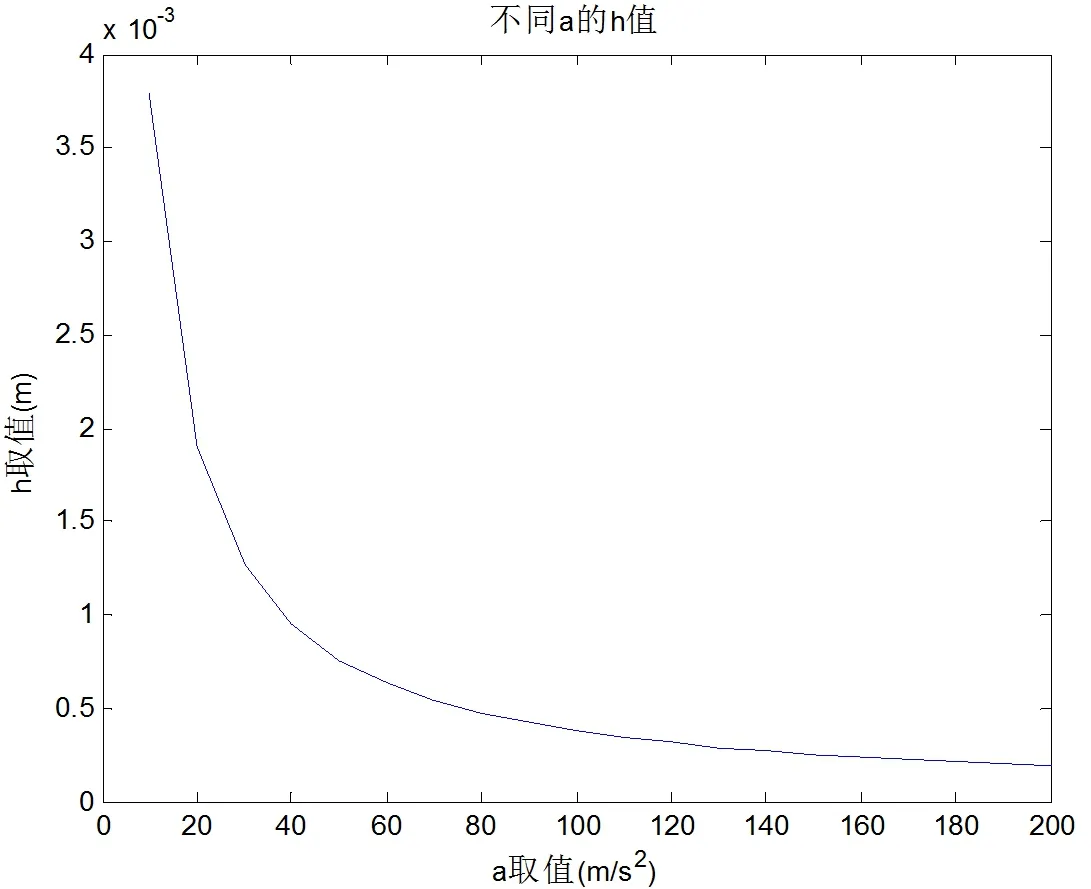
图3.3 两管液面高度差随加速度增加的变化趋势

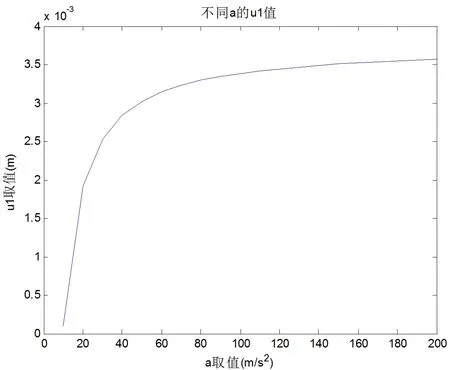
图3.4 水银液膜随加速度增加的位移变化

由图中可以看出，随着加速度的增大，两通道液面差值在缩小，加速度达到一定值后，两管液面高度趋向于齐平。微通道内水银位移随着加速的增大而增大，但在十倍于重力加速度后，升高幅度趋缓。

4 总结

论文研究探索新型原理的微加速度开关——利用水银作为介质的微加速度开关。最终目标是实现抗高过载的低量程，接触性好的加速度开关。下一步研究要分析不同管截面尺寸突变、串联与并联时的流动阻力，计算水银微通道及腔体、阀门空气缝隙和空气微通道的流动阻力；要进一步研究水银液面在不同加速度下的接触角变化趋势，将水银流体具有的惯性力用载体加速度与流体相对载体流动的加速度之和来表达，得到惯性力表达式，进而更精确可求得触点相对于载体的运动。

[1] 陈光焱,何晓平,施志贵等.开关点电可调节的MEMS冲击加速度锁定开关[J]..半导体学报.2007,8，Vol.28，No.8. 1295-07.

[2] 陈光焱,何晓平,施志贵等.准LIGA 微加速度开关的研制[J].微纳电子技术.2003, 8. 0312-02.

[3] 蒋炳炎，谢磊，谭险峰等. 流道截面形状对微流体流动性能的影响[J]..中南大学学报(自然科学版).2006,10, Vol.37，No.5. 0964-06.

[4] PFAHLER J，HARLEY J，BAU H.Liquid transport in micron and submicron channels[J].Sensors and Actuators，1990，22(1/3)：431-434.

[5] 李勇，江小宁，周兆英，等.微管道流体的流动特性[J].中国机械工程，1994，5(3)：24-25.

[6] 江小宁，周兆英，李勇等.微流体流动的试验研究[J].光学精密工程，1995，3(3)：51-55.

[7] 孔祥言.高等渗流力学[M]，中国科技大学出版社，1999:296-298.