流量测验流速仪法流量总不确定度的计算

克斯尔 ·卡合曼，谢 葆

(新疆巴音郭楞水文水资源勘测局，新疆巴音郭楞841000)

误差理论是一种研究各种测量值精度的数学方法，随着人类认识能力的不断发展，人们对测量结果准确度的要求愈来愈高。作为水文基础科学的一个重要内容流量测验，对测验误差中的各种测量的可能误差范围进行估算和评价，从而设法定量地评价流量测验精度，以进一步提高流量测验精度，满足水资源的开发利用和水利水电工程设计与施工对流量测验资料的各种要求，为防洪抗旱预报提供可靠精确的依据。

1 流量测验误差

流量测验误差可分为随机误差、未定系统误差、已定系统误差和伪误差。随机误差，按正态分布，采用置信水平为95%的随机不确定度描述。未定系统误差，采用置信水平不低于95%的系统不确定度描述。已定系统误差，应进行修正。含有伪误差的测量成果必须剔除。不确定度的数值应以百分数表示。

当采用流速仪法测流时，其误差应包括下列内容:(1)测深误差和测宽误差:测深误差和测宽误差由观读的随机误差和仪器本身所造成的未定系统误差组成。(2)流速仪检定误差:流速仪检定误差由检定的随机误差和仪器本身在测量中所造成的未定系统误差组成。(3)由测点有限测速历时导致的误差:流速仪法测流由测点有限测速历时导致的流速脉动误差(简称Ⅰ型误差)，为随机误差。(4)由测速垂线测点数目不足导致的垂线平均流速计算误差:测速垂线测点数目不足导致的垂线平均流速计算规则误差(简称Ⅱ型误差)，由随机误差和已定系统误差组成。(5)由测速垂线数目不足导致的误差:测速垂线数目不足导致的误差(简称Ⅲ型误差)，由随机误差和已定系统误差组成。

流速仪法的流量测验总不确定度应由流量测验总随机不确定度和总系统不确定度组成，并应按下列规定估算:

1)总随机不确定度应按下式估算:

式中:X＇Q为流量总随机不确定度(%);X'm为断面Ⅲ型随机不确定度(%);X'e为断面Ⅰ型随机不确定度(%);X'p为断面Ⅱ型随机不确定度(%);X'c为断面的流速仪率定随机不确定度(%);X'd为断面的测深随机不确定度(%);X'b为断面的测宽随机不确定度(%)。

2)总系统不确定度应按下式估算:

式中:X″Q为流量总系统不确定度(%);X″c为测宽系统不确定度(%);X″b为测深系统不确定度(%);X″d为流速仪检定系统不确定度(%);

3)总不确定度应按下式估算:

式中:XQ为流量总不确定度(%)。

流量测验成果应采用实测流量、总不确定度和已定系统误差三项数据表达。流速仪法的流量已定系统误差可按下式估算:

式中:μ^Q为流量已定系统误差(%);μ^m为Ⅲ型误差的已定系统误差(%);μ^s为断面Ⅱ型误差的已定系统误差(%)。

《河流流量测验规范》(GB 50179－93)，是全国水文站流量测验方法与分析计算方面的技术标准。是为保证流量测验精度和提供可靠的基础资料而制定的规范。但是在查算各种误差时，必须内插或是取上限值和下限值。使用起来比较繁琐，而且内插都是直线插补，人为误差较大。通过相关分析，有些数值不一定都是线性相关，而对数和指数相关关系比线性要好。在对各类误差相关分析时，一、二、三类精度的水文站，做了一点法的各类误差分析。采用相关最好的函数作为计算依据。对《河流流量测验规范》(GB 50179－93)中的各类误差查算表进行了统计分析工作，将查算表转换成相关方程，通过解方程直接计算出各类误差值。但这些方程求解起来比较困难，而且容易出现计算错误。可以利用EXCLE表格与VBA语言编写程序进行计算。以断面Ⅲ型随机不确定度计算表为例，如表1，先设m的初始值为整数“0”或“1”，得出方程初始值，设立“按钮”，输入实际值，按“按钮”计算。就方便、迅速、准确得到方程值。如此这样，计算出各分值，再算出流量总不确定度。

2 实例

现以塔里木河吾斯满水文站为例计算说明。乌斯满水文站位于巴音郭楞蒙古自治州尉犁县喀尔曲尕乡，地理位置为东经85°28'，北纬40°58'。其距上游英巴扎水文站179 km，距下游恰拉水文站219 km。测站观测项目有:水位、水温、流量、悬移质泥 沙等。主河道为自然河道，测流断面宽度约100 m。

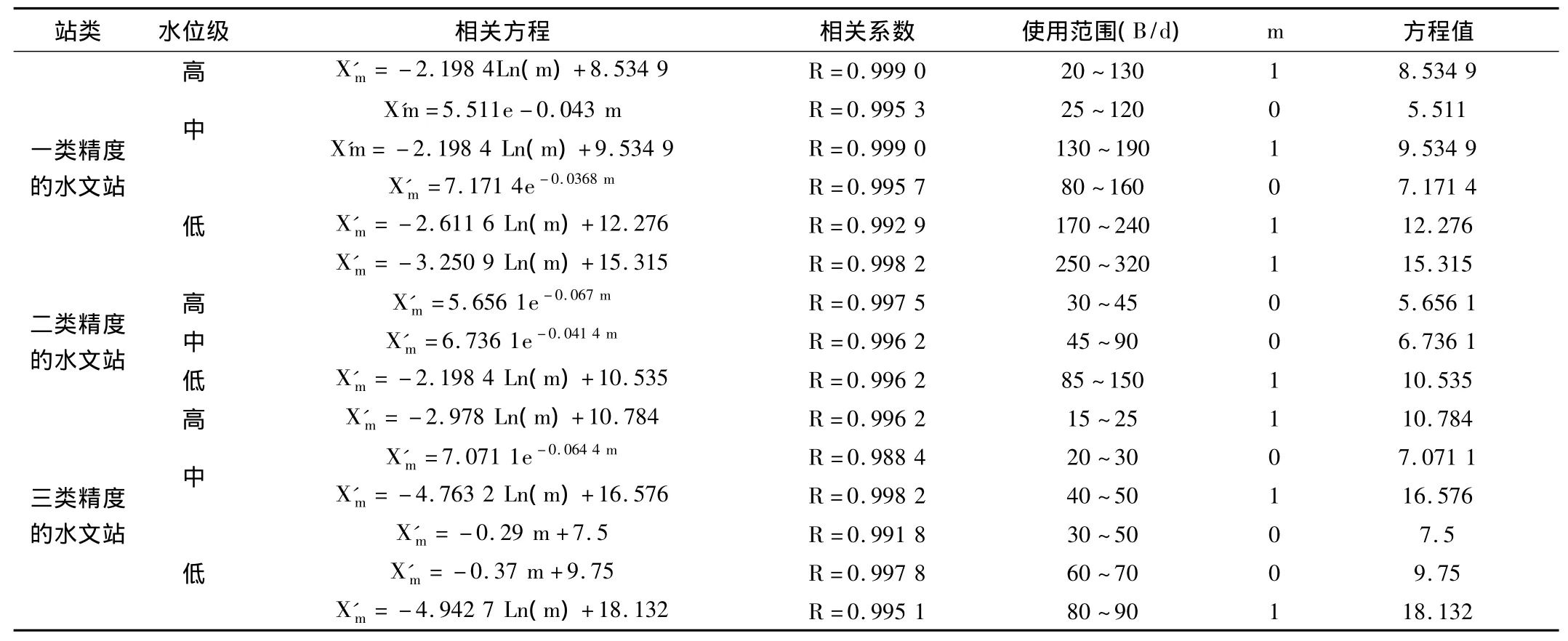
表1 断面Ⅲ型随机不确定度计算表

表2 吾斯满水文站流速仪法流量总不确定度计算成果表

计算结果如表2。从计算结果可得:乌斯满水文站断面高、中水位总随机不确定度、系统误差符合规范要求，但宽深比较大，说明流量测验值精度较高，符合规范要求;低水位系统误差偏小，而宽深比较小，流量测验值精度较低，需要分析，找出误差原因，改进测验方法。

3 结语

流速仪法的流量测验总不确定度计算时，参数较多。人工计算，费时，费力，比较困难，容易出错。而采用EXCLE表格及其VBA程序结合计算条理清晰，计算方法简便，计算成果精度高。给流量测验工作提供方便，提高工作效益。

［1］GB 50179－93河流流量测验规范 1994－02－01实施 中国计划出版社