小剪跨比RC梁受剪分析的优化拉压杆模型
贺志启 刘 钊
(东南大学土木工程学院,南京210096)
在小剪跨比钢筋混凝土梁中(剪跨比小于2左右),同时存在着“梁作用”和“拱作用”的双重受剪机制.上述2种机制的作用比例与很多因素相关,包括梁的剪跨比、配箍率和混凝土强度等,其中剪跨比是决定性因素[1-2].一般认为,对于剪跨比λ≤1的深梁,剪力主要通过“拱模型”直接传递至支座;对于λ≥2的浅梁,剪力主要经由“梁模型”进行间接传递;当1≤λ≤2时,这2种机制共同作用.
为了恰当反映小剪跨比RC梁内的复杂受剪机制,国内外学者提出了多种理论模型,如桁架拱模型[3]、拉压杆模型[4]等.这些模型均为超静定模型,难点是如何进行解耦分析.一种处理方式是假设模型中所有杆件均具有相同的轴向刚度,以此求解超静定模型[5-6];还有学者通过非线性有限元分析来求解超静定模型[7],其中模型中压杆的宽度根据支承情况确定,并假设拉杆能够达到屈服;本文作者也曾借助于拉压杆模型的最大强度建立准则,从理论上给出了“梁作用”和“拱作用”的解耦关系[8].
本文遵循能量原理的思路,通过3个层次的最小应变能分析,研究了小剪跨比RC梁受剪分析的最优拉压杆模型.该模型是静定模型,并且能够恰当表达小剪跨区域内的双重受剪机制.
1 拉压杆模型的最小应变能准则
拉压杆模型的理论基础是塑性下限定理,然而,混凝土材料的塑性变形能力有限,并不是塑料力学中所假想的理想刚塑性材料.因此,为避免出现超出混凝土塑性变形能力的应力重分布,拉压杆模型的变形应尽可能小,即为“最大刚度准则”.同时,结构的刚度和内部的应变能是直接相关的.对于能量封闭体系,能量守恒表现为外力功W等于结构应变能U,即

式中,P为外荷载;K为拉压杆模型的总体刚度;Fi,Li及εmi分别为拉压杆模型中第i根杆件的内力、长度及平均应变.
据此,可推演得到“最大刚度准则”等价于“最小应变能准则”,即

考虑到混凝土压杆的刚度远大于钢筋拉杆的刚度,因而拉压杆模型的应变能绝大部分集中在拉杆[4].因此,拉压杆模型的最小应变能准则可改写为

式中,Π为拉杆应变能指标;Ti和Li为第i根拉杆的内力和长度;εy为钢筋屈服应变.
本文遵循能量原理的思路,借助多层次的最小应变能分析,以此实现拉压杆模型的最优参数化构形.所提出的策略是:拓扑优化分析→STM基本构形→最小应变能分析→STM最优构形.即首先通过结构拓扑优化分析确定拉压杆模型的基本构形,然后针对由混凝土压杆和钢筋拉杆构成的拉压杆模型,进行最小应变能分析,以此推导模型的最优构形参数.
2 最小应变能拓扑优化分析
2.1 拓扑优化分析程序的开发
拉压杆模型的自动生成问题可转化为连续体的拓扑优化问题,并常常以最小应变能作为优化目标.在基于最小应变能指标的拓扑优化分析中,通过不断地从连续体中剔除应变能密度低的单元,最后实现结构总体刚度的极大化,即结构应变能的最小化.优化的目标函数可表示为[9]

式中,Cj为结构中单元j的应变能;Wj为单元j的重量.
若进一步定义结构性能指标ω,则优化目标是使得性能指标取得极大值,即

式中,下标“0”表示初始状态;“i”表示经过第 i次优化后的状态.
本文借助既有相关拓扑优化算法,通过对通用有限元程序ANSYS进行二次开发,实现了结构渐进拓扑优化功能,可实现平面和空间拉压杆模型的自动生成.该程序的编制框架为(见图1):程序不断地剔除低应变能密度的单元,直至有限元模型的连续性遭到破坏而不能运算为止;性能指标ω取得最大值时对应的拓扑构形,即为最优构形.编制该程序的关键技术包括:
①通过ANSYS程序中的生死单元功能来实现单元的剔除.
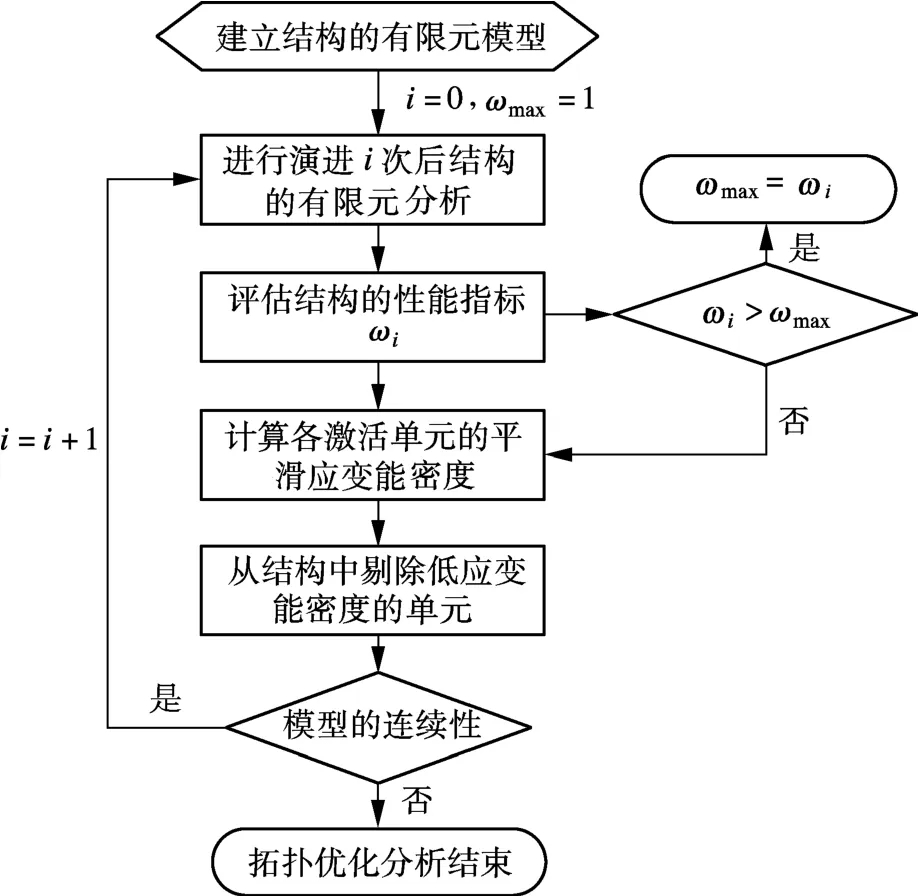
图1 拓扑优化程序框架
②通过三参数(ρe,R0和RΔ)来控制单元剔除的速度.通过单元移除率ρe来控制在每次演进过程中,剔除单元数量占总激活单元数量的最大比例(一般可取为5% ~10%);同时,通过下式来计算第i次演进时低应变能密度的阀值:

式中,[ζe,i]为第i次演进时低应变能密度的阀值,当单元的应变能密度小于该值时,应进行剔除;ˉζe,i为第i次演进时所有激活单元的应变能密度平均值;R0为初始比率,可取为1%;RΔ为演进速率,可取为1%.
③通过平滑化操作来避免棋盘式单元形态的出现.首先计算节点的平滑应变能(将与节点相邻单元应变能的平均值作为该节点的平滑应变能),然后计算单元的平滑应变能(将单元上4个节点平滑应变能的平均值作为该单元的平滑应变能).
2.2 小剪跨比梁的拓扑优化分析
针对跨中作用单点集中力的简支梁,进行了最小应变能拓扑优化分析,得到了不同剪跨比加载梁的最优拓扑构形(见图2),由图2可得:① 当剪跨比λ=1时,全部的集中荷载通过斜压杆直接传递至支座;②当剪跨比有所增大时,模型中出现了斜向拉杆,表明桁架模型开始发挥作用;③当剪跨比进一步增大,λ>2时,模型中出现多根间接斜压杆,说明桁架模型逐渐起主导作用.

图2 不同剪跨比梁的最优拓扑构形架
至此,借助于拓扑优化分析的结果,可以确定小剪跨比梁中拉压杆模型的基本构形为:① 当λ≤1时,最优模型为“直接压杆模型”.该模型中的斜压杆为集中力作用点与支座中心的连线,易于确定.②当1<λ≤2时,最优模型为“带斜拉杆的桁架模型”(见图2(b)、(c)).在无腹筋梁中,斜拉杆为混凝土拉杆;在有腹筋梁中,斜拉杆由腹筋构成.该模型中存在3根倾角不同的斜压杆,但目前还无法定量确定其几何参数.
3 最小应变能参数分析
为了定量计算深梁(1<λ≤2)中拉压杆模型的斜压杆倾角,这里进行了2个层次的最小应变能参数分析.
3.1 最小应变能自动搜索
利用编制的算法,自动搜索应变能最小的拉压杆模型构形.模型的基本形状如图3(a)所示,模型中节点B(或节点C)的位置可在竖向和水平向2个方向变动,节点E(或节点F)的位置可在水平方向变动.算法的基本结构如下:① 分层变化拉压杆模型的几何参数x1(0→a),x2(0→d)和x3(0→a);②提取每种模型中所有拉杆的内力Ti和长度Li,并计算应变能指标∑TiLi;③搜索应变能指标最小的拉压杆模型,即为最优模型.
针对不同剪跨比的深梁,按上述算法可自动搜索得到拉压杆模型的最优几何参数(x1,x2和x3),如表1所示.通过对这些最优拉压杆模型的几何形状进行观察,可以发现以下规律:①杆件AE和BE大体上呈垂直关系;②杆件 AE和BD大致平行.根据这些规律,可用图3(b)所示的简化模型来代替前述最优模型,该模型中只存在斜压杆倾角θ这一单参数.

图3 集中荷载作用深梁(1<λ≤2)的拉压杆模型
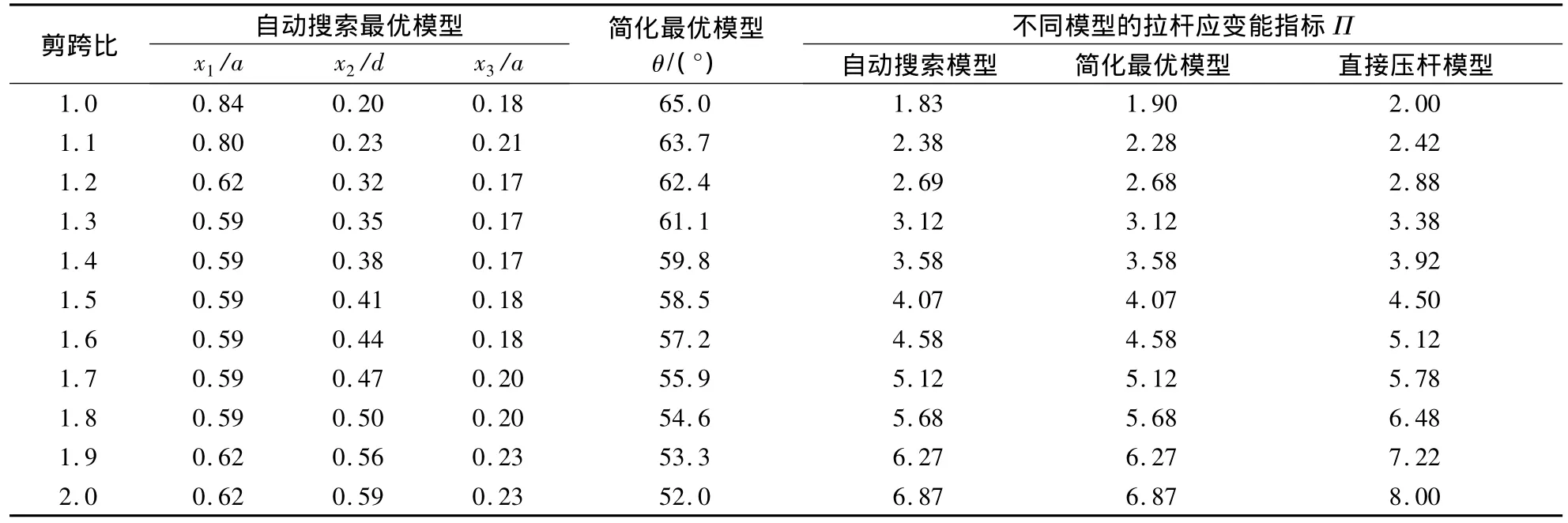
表1 集中荷载作用深梁(1≤λ≤2)的最优拉压杆模型参数
3.2 最小应变能目标函数求解
针对图3(b)所示的单参数简化模型,基于最小应变能原理,直接推导斜压杆倾角θ的最优取值.在简化模型中,拉杆的应变能分析如表2所示.

表2 简化模型中的拉杆应变能分析
半模型中拉杆的应变能指标为

为使应变能取得最小值,斜压杆倾角θ应满足

因此,斜压杆倾角θ的最优取值可求解为

同时,可求得最优模型中斜拉杆BE的内力为

在无腹筋梁中,该斜向拉力由受拉混凝土承担;在有腹筋梁中,主要由腹筋承担.
在表1中,除列出了最优模型的几何参数外,还列出了不同模型的应变能指标.可以发现,虽然“直接压杆模型”中的荷载传递最为直接,但其拉杆应变能并不是最小的.只有当梁的剪跨比λ接近于1时,“直接压杆模型”中的应变能才与最优的“带斜拉杆的桁架模型”的应变能相差无几.
3.3 最优拉压杆模型的特征
通过前述3个层次的最小应变能分析(最小应变能拓扑优化分析、最小应变能自动搜索和最小应变能目标函数求解),确定了小剪跨比RC深梁的最优拉压杆模型构形,该模型具有以下特征:①当梁的剪跨比λ≤1时,受剪分析的最优模型为“直接压杆模型”,此时剪力荷载通过斜压杆直接传递至支座;②当梁的剪跨比1<λ≤2时,受剪分析的最优模型为“带斜拉杆的桁架模型”(见图3(b)),斜拉杆与斜压杆大体上呈垂直关系,而斜压杆倾角θ与剪跨比λ直接相关,其最优角度为θ=78-13λ.
4 无腹筋小剪跨比梁的抗剪强度
在无腹筋小剪跨比RC梁中,拉压杆模型中的斜向拉杆表征了混凝土的受拉作用.当混凝土斜拉杆断裂时,可反映无腹筋梁劈裂破坏时的抗剪承载力,即
式中,WBE为斜向拉杆的宽度,可假设为与之垂直压杆 AE 长度的一半[10],即 WBE=0.5d/sinθ;TBE为斜向拉杆的内力,可按式(10)计算;b为腹板厚度;ft为混凝土轴心抗拉强度,可按ft=0.5(fc)2/3进行换算,fc为混凝土棱柱体抗压强度.
根据式(11),抗剪承载力可推导为

将斜压杆倾角θ的最优取值代入式(12),并经最小二乘拟合,最终可得无腹筋小剪跨比RC梁抗剪承载力的简化计算式为

式中,λ≤2.
为验证本文所提抗剪强度计算公式的正确性,与文献[11]收集的20根无腹筋短梁的抗剪承载力试验值进行对比,如图4所示.由此可见,本文公式能够较好地反映剪跨比对无腹筋梁抗剪承载力的影响,并且与 GB50010—2010规范[12]中的式(6.3.4)相比,本文所提出的理论公式与试验数据拟合线更为接近,有更好的计算精度.

图4 无腹筋RC深梁抗剪承载力试验值与计算值的对比
5 结论
1)提出了确定拉压杆模型最优构形的“多层次最小应变能分析方法”.该方法首先借助结构拓扑优化分析拟定拉压杆模型的基本构形,并利用最小应变能参数分析确定模型的最优构形参数,具有适应能力强、参数化建模等特点.
2)小剪跨RC梁内存在着复杂的受剪机制,当梁的剪跨比λ≤1时,剪力荷载通过“拱模型”直接传递至支座;当1<λ≤2时,剪力荷载通过“带斜拉杆的桁架模型”进行间接传递,模型中斜拉杆与斜压杆大体上呈垂直关系,而斜压杆倾角θ与剪跨比λ直接相关,其最优角度为θ=78-13λ.
3)本文依据拉压杆模型所提出的无腹筋小剪跨比梁抗剪承载力计算式,形式简洁,并且能够较好地反映剪跨比的影响.
References)
[1] Fenwick R,Paulay T.Mechanisms of shear resistance of concrete beams[J].Journal of Structural Engineering,ASCE,1968,94(10):2325-2350.
[2] Mihaylov B,Bentz E,Collins M.Behavior of large deep beams subjected to monotonic and reversed cyclic shear[J].ACI Structural Journal,2010,107(6):726-734.
[3] 刘立新.钢筋混凝土深梁、短梁和浅梁受剪承载力的统一计算方法[J].建筑结构学报,1995(4):13-21.Liu Lixin.An unified calculation method for shear capacity of RC deep beams,short beams and shallow beams[J].Journal of Building Structures,1995(4):13-21.(in Chinese)
[4] Schlaich J,Schäfer K,Jennewein M.Toward a consistent design of structural concrete[J].Journal of the Prestressed Concrete Institute,1987,32(3):74-150.
[5] Matamoros A,Wong K.Design of simply supported deep beams using strut-and-tie models[J].ACI Structural Journal,2003,100(6):704-712.
[6] Yang K,Ashour A.Strut-and-tie model based on crack band theory for deep beams[J].Journal of Structural Engineering,ASCE,2011,137(10):1030-1038.
[7] Kim B,Yun Y.An indeterminate strut-tie model and load distribution ratio for RC deep beams(Ⅰ)model&load distribution ratio[J].Advances in Structural Engineering,2011,14(6):1031-1041.
[8] He Z,Liu Z,Ma Z.Investigation of load transfer mechanisms in deep beams and corbels[J].ACI Structural Journal,2012,109(4):467-476.
[9] Liang Q,Xie Y,Steven G.Topology optimization of strut-and-tie models in reinforced concrete structures using an evolutionary procedure[J].ACI Structural Journal,2000,97(2):322-332.
[10] Al-Nahlawi K,Wight J.Beam analysis using concrete tensile strength in truss models[J].ACI Structural Journal,1992,89(3):284-290.
[11] 熊进刚,付国平.钢筋混凝土无腹筋短梁受剪承载力计算的软化桁架模型[J].南昌大学学报:工科版,2004,26(1):49-53.Xiong Jingang,Fu Guoping.Softened truss model for calculation of shear capacity of reinforced concrete short beams without web reinforcement[J].Journal of Nanchang University:Engineering& Technology,2004,26(1):49-53.(in Chinese)
[12] 中华人民共和国住房和城乡建设部.GB 50010—2010混凝土结构设计规范[S].北京:中国建筑工业出版社,2010.

