基于回采工作面流场分布的拖管抽采瓦斯参数模拟研究＊

孙晓元 王 川 孙英峰 邢云峰

（1.太原科技大学环境与安全学院，山西省太原市，030024；2.中国矿业大学 （北京）资源与安全工程学院，北京市海淀区，100083；3.北京起重运输机械设计研究院，北京市东城区，100007）

受地质构造、煤层赋存及采掘方式多方面因素的影响，回采工作面及采空区的瓦斯流场表现为明显的不均衡性和多变性。这种特点在以较快开采速度和较高开采强度为特征的现代综合机械化采煤工艺中体现的尤为突出。作为典型的高瓦斯且具有煤与瓦斯突出危险的矿井，华晋焦煤集团沙曲矿开采的4＃煤层瓦斯压力为1.52～1.57 MPa，瓦斯含量为7.3～17.82m3／t。根据现场测定，煤层透气性系数为1.577～3.999 m3／MPa2·d，衰减系数0.01～0.016 （100d-1），抽放难度较大。而传统的埋管抽放方式受空间非连续性的限制，尚未达到理想的抽放效果。鉴于此，亟需采用拖管抽采技术来改进采空区抽放方法，并在对工作面和采空区瓦斯流分布特征进行准确的理论分析和数值模拟基础上，确定最佳抽放点位置和合理抽放参数，为实际应用提供技术支持。

1 风流在采场中的运动模型

将风流从进入工作面进风巷，流经工作面 （部分漏风流经采空区），然后从回风巷排出的整个过程视为研究对象，该过程包括风流在自由空间中的湍流过程和多孔介质 （采空区）的快速流动过程，两种过程所表现的流动方式不同，遵循的控制方程也有所差异。

1.1 风流在自由空间中的流动方程

由于巷道和工作面正常通风时其雷诺准数远大于临界雷诺数，因此国内外学者往往从Navierstokes方程出发来描述其物理性质。当风流为定常流动 （定常粘度、不可压缩，即η，ρ=const）时，其平面二维动量表达式 （N-S方程）为：

式中：u——风流在自由空间中的速度矢量，m／s；

ρ——风流密度，kg／m3；

p——风流压力，Pa；

ν——风流的运动粘度，m2／s；

f——单位质量风流的体积力，N／kg。

式中：η——风流的动力粘度，Pa·s。

由式 （2）和 （3）可以看出，定常流动N-S方程的因变量包括速度矢量u和压力标量p，为讨论方便，将其用下标 “ns”来表示。

1.2 风流在多孔介质中的流动方程

根据O 形圈理论，在距离工作面30m 范围内的采空区裂隙较为发育，且此范围内有较高速度的漏风流经过。实测表明，采空区内的风流基本上属于介于N-S自由流动和Darcy渗流之间的快速过渡流动，因此，可以选用Brinkman方程对其进行描述：

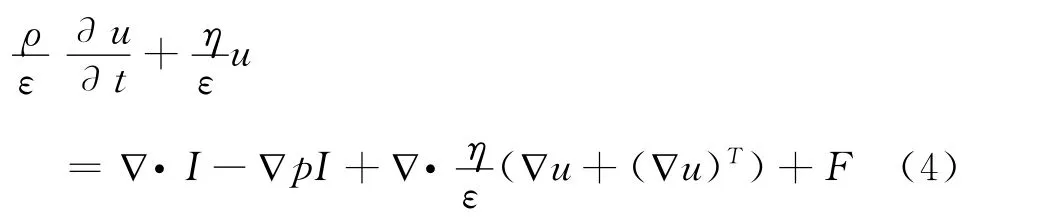
式中：ε——多孔介质的孔隙率；

I——单位矢量；

F——流体阻力，N。

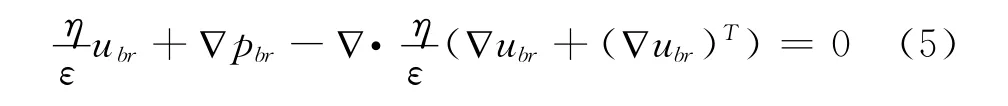
同样，根据质量守恒方程可以得出：

式（5）和 （6）组成了风流在多孔介质中运移的控制方程，可以看出，Brinkman方程的因变量包括速度矢量u和压力标量p，为讨论方便，将其用下标 “br”来表示。

1.3 风流运动模型

通过上述分析可知，利用N-S方程和Brinkman方程可以较好描述风流在自由空间和多孔介质中的流动过程，因此可以将两者联合起来构建风流从进入进风巷道并流经工作面 （部分经过采空区）直至流出回风巷道的运动模型，如图1所示。实际上，将控制方程 （2）、（3）、（5）和 （6）联立起来即可对工作面及采空区的流动速度和压力分布进行求解，但要注意边界的连续性，即在漏风界面上存在uns=ubr和pns=pbr。

在进行理论分析和数值模拟时，需考虑采空区渗透率和孔隙率的分布问题，即受O 形圈影响不同的区域会有所差异。一般情况下，这些参数和碎胀性系数Kp（x，y）存在函数关系。而碎胀性系数的表达式为：

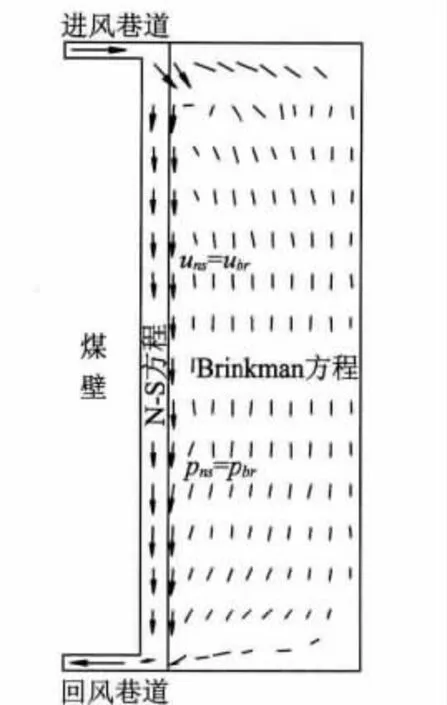
图1 风流运动模型

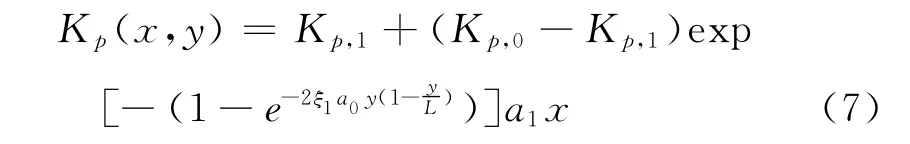
式中：Kp，0——初次冒落的碎胀系数；

Kp，1——压实后的碎胀系数；

a0、a1、ξ1 ——调整系数；

L——工作面长度，m。

2 瓦斯在采场中的运移模型

上述讨论研究了风流在采场中的运动规律，然而往往更要关注的是瓦斯在采场中的运移特征。为此，将瓦斯在采空区的运移分为浓度扩散和对流运移两个过程来进行讨论，这是因为若单纯考虑Fick扩散第二定律来描述平面二维尺度空间内的瓦斯非稳定流动场时，其方程表达式为：

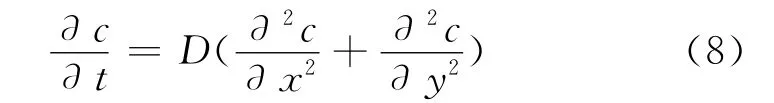
式中：c——瓦斯浓度，mol／m3；

D——扩散系数。

显然，式（8）是基于纯浓度梯度 （即浓度为唯一驱动力）和质量守恒定理得到的。但对于所要重点研究的采空区上隅角及其附近裂隙较为发育的区域则有所不妥，这是因为该区域有较高速度的流体经过，瓦斯运移的驱动力还应包括通风对流；该区域的瓦斯是存在有源补充的，汇源项包括遗煤及深部采空区不断向外涌出的瓦斯。因此，需要将式（8）加以完善，改写为：

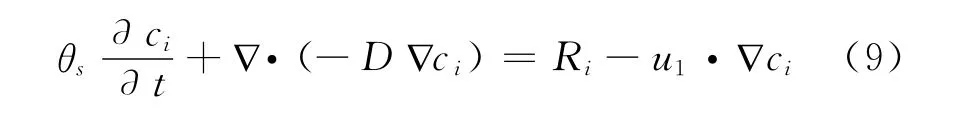
式中：θs——瓦斯瞬时比例系数；Ri——汇源项；

u1——瓦斯平均流速，m／s。

关于平均流速的计算模型，文献采用Darcy方程来进行刻画，鉴于本文研究区域的特殊性，故采用Brinkman方程来描述速度场分布，即联立公式（5）、（7）和 （9）来探讨采空区裂隙发育带及上隅角附近的瓦斯运移规律。

3 瓦斯在抽放渗流场中的运移模型

在对瓦斯进行抽放时，其有效抽放影响范围内瓦斯的流动满足质量守恒方程：

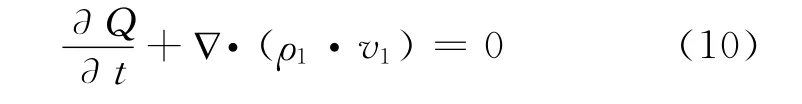
式中：Q——单位体积煤岩体所含有的瓦斯量，

kg／t；

v1——钻孔周边的瓦斯渗流速度，m／s；ρ1——瓦斯密度，kg／m3。

显然，单位体积煤岩体中的瓦斯含量应包括吸附瓦斯含量和游离瓦斯含量两部分。其中吸附瓦斯含量由Langmiur等温吸附方程求得：

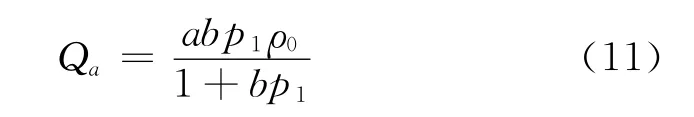
式中：Qa——吸附瓦斯含量，kg／t；

p1——瓦斯压力，MPa；

a——吸附常数，单位体积煤体的极限瓦斯吸附量，m3／t；

b——吸附常数，MPa-1；

ρ0——标准大气压下的瓦斯密度，kg／m3。

与之相对应的，若将瓦斯渗流视为理想气体在不考虑吸附解吸的等温过程时，游离瓦斯含量为：

式中：Qf——游离瓦斯含量，kg／t；

ε——多孔介质的孔隙率；

β——瓦斯气体的压缩因子，kg／m3·Pa。

显然，存在公式：

假设瓦斯在煤层中的渗流模式为达西流动，并考虑Klinkenberg效应，则渗流的速度为：

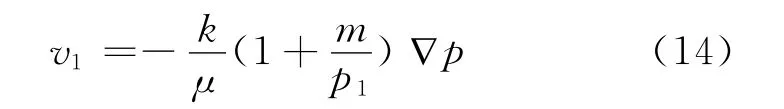
式中：k——煤岩的渗透率，m2；

v1——渗流速度，m／s；

μ——瓦斯的动力粘度系数，Pa；

∇p——压力梯度；

m——Klinkenberg等效因子。若考虑等温过程多孔介质孔隙率的变化：

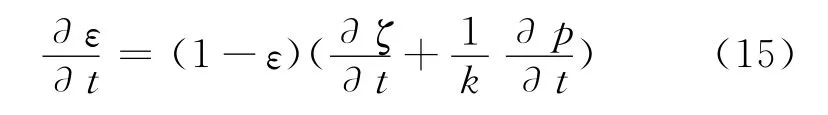
式中：ζ——含瓦斯煤岩的体积应变。

将式 （11）～ （15）联立可得瓦斯在抽放渗流场中运移的控制方程为：

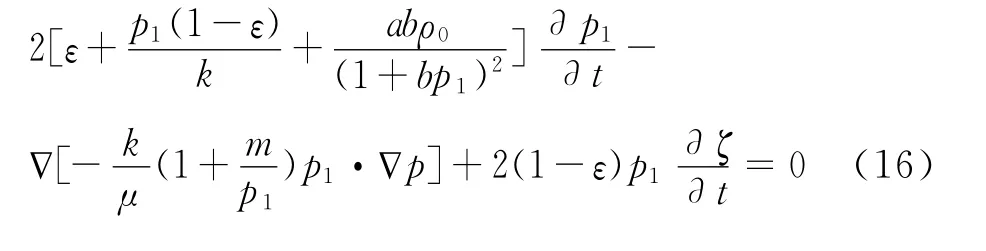
4 数值模型及结果分析

通过上述分析，求得回采工作面风流与瓦斯的流场分布及抽放渗流场控制方程的解析解是十分困难的，这是因为这些方程绝大部分都含有一阶或二阶偏微分项。因此，可以专门采用基于偏微分方程的有限元求解平台COMSOL Multiphysics多物理场耦合分析工具。

4.1 几何模型

算例选用沙曲矿14205综采工作面，工作面长度为158m，高度2.5m，进风巷和回风巷净断面尺寸为4m×2.5m，采空区冒落带高度为8m，为模拟O形圈内的瓦斯运移规律，走向长度选为50m。

4.2 初始值和边界条件

在14205综采工作面正常回采期间的生产班和非生产班多次测定其进回风巷和工作面的风速、风量和瓦斯浓度等参数。通过统计分析，相关初始条件与其他边界条件的取值：进风巷风速172m／min，进风巷风量1800m3／min，空气密度1.29kg／m3，空气动力粘度5×10-5Pa·s，瓦斯动力粘度1.34×10-5Pa·s，煤壁瓦斯涌出量34.21m3／min，落煤及遗煤瓦斯涌出量14.5m3／min，内部采空区瓦斯涌出量49.85m3／min，工作面、采空区初始气体压力0.1MPa，采空区初始瓦斯浓度3mol／m3，瓦斯分子扩散系数0.0756 m2／h，采空区初始碎胀系数1.5，抽放管路负压2kPa。

图2 风流在采空区和工作面运动模型的浓度分布云图

4.3 模拟结果分析

单独模拟风流在采空区和工作面运移时速度和浓度场分布，如图2所示。其中在工作面运动方程采用N-S 方程，在采空区 （多孔介质）中采用Brinkman方程来刻画速度场，将上述两方程求得的速度场带入空气溶质的对流传递中，以实现方程的耦合。图2中横坐标代表模拟的不同时刻，从图中可以看出，风流大部分经工作面由回风巷排出，少部分风流进入采空区。由于采空区各处碎胀性系数设置的不同，其渗透率也有所差异。风流在进入采空区后，受风流方向及渗透率的影响，采空区靠近进风巷及工作面的位置空气浓度首先上升，原因是其区域位于O 形圈范围内。而中部区域由于渗透率较低，其浓度比O 形圈内要低，见图2 （c），但随着时间步的推移，中部区域的浓度也逐渐上升，说明瓦斯也逐步流入此区域，见图2 （d），并最终达到平衡。

图3模拟的是未采取抽放措施时采空区和工作面的瓦斯体积分数分布云图。其中瓦斯在采空区（多孔介质）的平移扩散时的速度场为Brinkman方程的模拟结果。由图3可以看到，虽然在初始值设置的时候将采空区的瓦斯浓度预定为3mol／m3，并且有内部采空区和落煤 （遗煤）瓦斯的涌入，随着时间的推移，采空区中高瓦斯浓度所占有的区域逐渐减小，并呈现出一定的规律性，即倾向方向上越接近进风巷瓦斯体积浓度越低，下降的速度越快，而越接近回风巷道瓦斯体积浓度越高，且浓度下降的速率越慢；走向方向上瓦斯体积浓度随深度的增大而逐渐增加；垂向方向上随高度的增大瓦斯体积浓度也在增大；采空区中部渗透率较低区域的瓦斯浓度下降速率小于O 形圈范围，说明在裂隙发育带的气体流动速率较快。

图3 未采取抽放措施时采空区及工作面的瓦斯体积浓度分布云图

图4显示的是抽放前后采空区及工作面瓦斯体积分数与浓度等值面对比图，这里采用了以缝代孔的方式来模拟抽放。通过分析可以发现，虽然单纯利用通风可以降低采空区及工作面的瓦斯，但一方面降低的速率较慢，另一方面在上隅角附近尤其是“三角区”范围内的瓦斯浓度依然较大，如图4（b）所示，仍存在发生瓦斯事故的危险。因此，有必要采取抽放措施。图4 （c）～4 （f）显示了拖管抽放后的采空区及工作面瓦斯体积浓度等值面图和分布云图，对比图3 （a）和图3 （b），拖管抽放后上隅角瓦斯浓度迅速下降，抽放100000s后上隅角瓦斯浓度降为10.9%，其效果与未抽放1000000s时单纯靠通风降低瓦斯的效果 （9.27%）基本相似，当拖管抽放1000000s时，上隅角附近的瓦斯浓度已降到了5.97%。经过模拟发现，随着时间的推移，当拖管抽放时间达到2000000s时，上隅角的浓度降为0.9%，若能对上隅角进行适当的封堵，减小该区域的渗透率，将能进一步降低上隅角的瓦斯浓度并提高抽放效率。

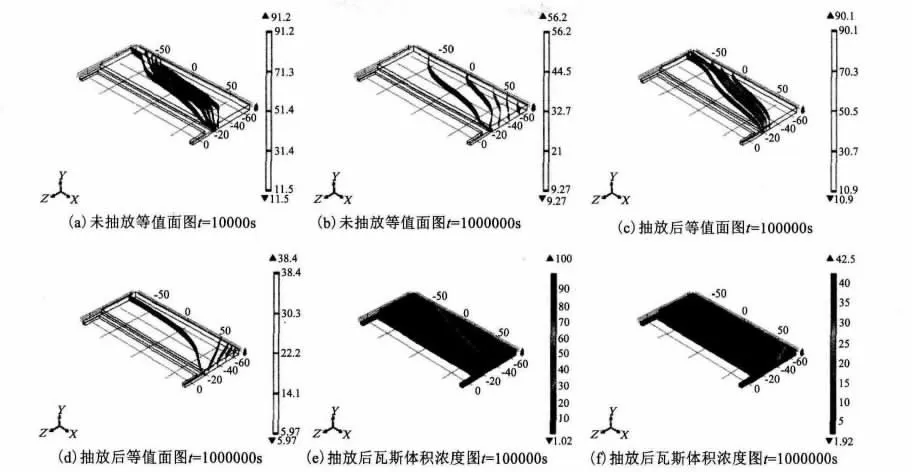
图4 拖管抽放前后等值面与瓦斯体积分数对比图

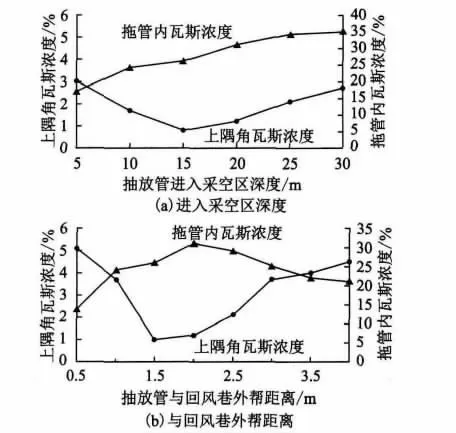
图5 拖管抽放深度及与回风巷外帮距离参数的确定

为了确定14205综采工作面拖管的合理位置，需要对不同高度、深度及距回风巷外帮位置处的瓦斯抽放效果进行模拟。显然，抽放管内的瓦斯浓度随高度的增加而增大，这是由瓦斯的升浮弥散特性所决定的。由此，只需要根据现场实际情况将瓦斯抽放拖管的位置抬到工程允许的适合高度即可，这里将其确定为2.3m。图5显示的是不同抽采深度和距离外帮不同位置时，上隅角及抽放管内瓦斯浓度（抽放时间均为2000000s），上隅角的取样位置选择在采空区纵深1m、距离底板2.3m、距回风巷外帮0.3 m 处，抽放管的取样位置选择在抽放管内距离瓦斯流出点1 m 处。由图5 （a）可以看出，随着抽放管进入采空区深度的增加，拖管内的瓦斯浓度也在逐渐上升，但当拖管抽放口进入采空区深度过大时，其距离工作面较远，上隅角位置的瓦斯浓度控制效果较差，从安全考虑，选择进入采空区深度为15m 为宜；由图5 （b）可以看出，由于采空区瓦斯流场分布的复杂性，抽放管并非越接近回风巷外帮越好，确定准则应综合上隅角瓦斯浓度及拖管内瓦斯浓度综合考量，经过分析，选择在距离外帮1.5m 处为宜。

综上所述，沙曲矿14205综采工作面拖管抽采的合理抽放参数为抽放高度2.3m，拖管进入采空区深度15m，抽放位置距离回风巷外帮1.5m。

5 结论

（1）采用COMSOL Multiphysics多物理场耦合分析工具可以合理准确的研究回采工作面与采空区的速度场和浓度场特征，同时也可利用该工具来对拖管抽采措施进行效果考察，从而为工程实践提供了一定的参考依据。

（2）风流在自由空间内的运动规律遵循Navier-stokes方程，而在采空区O 形圈内遵循Brinkman方程。同样，瓦斯在采空区内的速度场分布也符合Brinkman方程。风流和瓦斯气体的混合过程为对流扩散和溶质传递过程，运用上述方程可以很好地刻画工作面和采空区的流场分布规律。

（3）由于沙曲矿14205综采工作面的特殊性，有必要采取拖管抽放措施。合理的抽放参数为抽放高度2.3m，拖管进入采空区深度15m，抽放位置距离回风巷外帮1.5m。

［1］ 吴兵，雷柏伟等.回采工作面上隅角瓦斯拖管抽采技术参数研究 ［J］.采矿与安全工程学报，2014（2）

［2］ 李东印，许灿荣等.采煤工作面瓦斯流动模型及COMSOL数值解算 ［J］.煤炭学报，2012 （6）

［3］ 章争荣，张湘伟.二维定常不可压缩粘性流动N-S方程的数值流形方法 ［J］.计算力学学报，2010（3）

［4］ 钱鸣高，许家林.覆岩采动裂隙分布的 “O”形圈特征研究 ［J］.煤炭学报，1998 （5）

［5］ 张人伟，贺晓刚等.朱仙庄矿综放面采空区 “三带”范围的确定及应用 ［J］ .采矿与安全工程学报，2008 （3）

［6］ 杨天鸿，陈仕阔等.采空垮落区瓦斯非线性渗流-扩散模型及其求解 ［J］.煤炭学报，2009 （6）

［7］ Brinkman H C.A calculation of the viscous force exerted by flowing fluid on a dense swam of particles［J］.Applied Scientific Research，1947 （1）

［8］ 李宗翔，衣刚等.基于 “O”型冒落及耗氧非均匀采空区自燃分布特征 ［J］.煤炭学报，2012 （3）

［9］ 杨其銮，王佑安.煤屑瓦斯扩散理论及其应用 ［J］.煤炭学报，1986 （3）

［10］ 李宗翔，纪书丽等.采空区瓦斯与大气两相混溶扩散模型及其求解 ［J］.岩石力学与工程学报，2005（16）

［11］ 杨天鸿，徐涛等.应力-损伤-渗流耦合模型及在深部煤层瓦斯卸压实践中的应用 ［J］.岩石力学与工程学报，2005 （16）

［12］ 马海峰，王磊等.掘进煤巷瓦斯渗流模型及运移规律研究 ［J］.中国煤炭，2013 （8）

［13］ 李培超，孔祥言等.饱和多孔介质流固耦合渗流的数学模型 ［J］ .水动力学研究与进展 （A 辑），2003 （4）

［14］ 尹光志，李铭辉等.基于含瓦斯煤岩固气耦合模型的钻孔抽采瓦斯三维数值模拟 ［J］ .煤炭学报，2013 （4）

［15］ 刘华锋，陈辉等.顺层钻孔瓦斯抽采半径确定及抽采效果考察研究 ［J］.中国煤炭，2013 （6）

［16］ 黄志安，张英华等.FLAC 在确定沙曲矿裂隙带上下界中的应用 ［J］.矿业研究与开发，2006 （1）

［17］ 王恩志，王洪涛等 .“以缝代井列”——排水孔幕模拟方法探讨 ［J］.岩石力学与工程学报，2002（1）

［18］ 李宗翔，王继仁等.采空区开区移动瓦斯抽放的数值模似 ［J］.中国矿业大学学报，2004 （1）

［19］ 郭玉森，林柏泉等.围岩裂隙演化与采动卸压瓦斯储运的耦合关系 ［J］ .采矿与安全工程学报，2007 （4）

［20］ 邢云峰，孙晓元，孙英峰.合理钻孔间距和瓦斯抽放时间的理论分析与数值模拟 ［J］ .中国煤炭，2014 （5）