避难硐室围岩与空气耦合传热机理研究＊

张祖敬 何廷梅

（中煤科工集团重庆研究院有限公司，重庆市北碚区，400037）

煤矿避难硐室是为灾区遇险人员提供安全避灾环境的井下密闭硐室，是煤矿井下优先建设的紧急避险设施。研究表明，人员静坐或轻度劳动时，产热量86～130 W。避灾过程中，若无降温措施，人体代谢和设备运行产生的热量将引起硐室环境温度升高。高温热环境中，人体热平衡遭到破坏，体内未散出的热量将导致体温升高，引发热病，甚至死亡。为保证人员生命安全，需采取降温措施，使环境温度维持在人体热耐受范围。

热负荷计算是硐室降温设计的基础前提。本文借助半无限大物体传热理论，推导出避难硐室内无降温措施条件下的空气升温规律计算公式和硐室内维持恒温时围岩结构与空气耦合传热计算公式，借助Fluent软件，对两阶段的传热过程进行数值分析。

1 煤矿避难硐室传热模型简化

针对地下建筑传热，黄福其、冯金秋等根据埋深不同，将地下建筑分为深埋地下建筑 （埋深＞12 m）和浅埋地下建筑；根据几何形状不同，分为长洞 （长／宽≥2）和短洞，在研究深埋地下建筑热传导过程时，把地下建筑矩形横断面当量化为圆形，对维护结构内表面的平均温度以及传热量的影响极小。结合煤矿井下埋深及避难硐室形状，可将避难硐室简化为当量圆柱体深埋地下密闭建筑传热模型。

根据避难硐室内是否采取降温措施及室内环境温度变化情况，将避难硐室内的热工传递过程分为升温阶段 （未采取降温措施时室内空气升温过程）和恒温阶段 （空气升温到一定温度后采取降温措施使空气温度维持相对稳定的过程）两个阶段。

2 传热理论分析

2.1 升温阶段传热理论分析

避灾时期，人员常保持坐姿，产热相对稳定，个体差异小，可视为恒功率热源。由于空气密度与比热较小，空气的吸收热量远小于围岩导出的热量，可认为硐室内热源单位时间内产生的热量全部由壁面通过对流换热传出。供给硐室壁面围护结构内表面单位面积的热量q可视为均匀分布，则有：

式中：q——围岩表面热流密度，W／m2；

Q——室内热源功率，W；

A——围岩表面面积，m2。

根据恒热流密度条件下半无限大物体传热理论，得出τ时刻硐室内空气温度t（0，τ）为：

式中：a——围岩热扩散系数，m2／h；

λ——围岩导热系数，W／ （m·K）；

τ——时间，h；

α——对流换热系数，W／ （m2·K）；

r0——硐室当量半径，m；

t0——围岩初始温度，℃；

F0——傅立叶准数。

2.2 恒温阶段传热理论分析

假定避难硐室生存的室内空气温度达到规定值t（0，τ）=tn后，硐室内空气温度一直维持在tn值，硐室岩体内的温度仍保持岩石的初始温度t0，且认为此阶段的时间从零时刻开始，则由导热微分方程、初始条件及边界条件，可列出如下方程组：

式中：r——围岩当量半径，m；

t（0，τ）——τ时刻r 处围岩温度，℃。

由方程组 （4）可得硐室围岩表面温度为：

式中：Bi——毕渥数；

f1（F0，Bi）——引入函数。

由牛顿冷却定律可得围岩表面热流密度为：

实际过程中，硐室传热过程的恒热流传热期与恒温传热期是连续的，即恒热流传热期结束便是恒温传热期的开始。因此，恒热流密度传热期结束时与恒温传热期开始时的硐室壁面热流密度应相等。经升温过程避难硐室内空气温度达到tn值后，硐室围岩壁面及内部温度发生改变。假设恒温传热期从初始时刻起在t2时刻时，避难硐室内壁面的热流量与恒热流传热期结束τ1时刻的热流量相等，即：

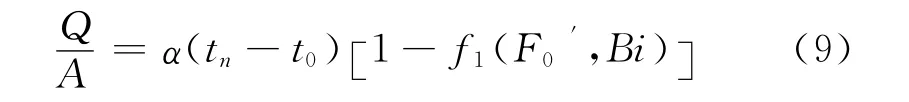
则有：

式中：τ2——恒温传热开始时的时间。

计算恒温使用时期某时刻τ的传热量，按τ=τ+τ2代入式 （8）计算即可。

硐室围岩调热圈半径计算公式：

3 数值计算分析

以51 人煤矿避难硐室作为研究模型，采用Fluent软件模拟避难硐室内空气与岩体围护结构的三维动态耦合传热过程。

3.1 几何模型建立与边界条件设置

避难硐室围岩种类以砂岩、泥岩、石灰岩居多，热扩散系数a 取值范围为15×10-4～50×10-4m2／h。经计算，96h 内，硐室围岩调热圈半径最大为2.25 m，模型中取围岩厚度为2.5 m。室内为拱形断面，长17m、宽4m，51人呈17排3列分坐于硐室内。将人体模型简化为圆柱体。放置3台空气净化降温一体机 （简称一体机），硐室内的空气通过一体机底面的矩形进风口进入一体机，然后通过前侧上方的圆形出风口将风流送入硐室。一体机的进风口离地面高度0.2m。一体机可为避难硐室内环境降温，为硐室内的空气净化提供风流循环动力，不考虑一体机内部空气净化过程与空气降温过程，结合一体机风流进、出口，对一体机外形进行简化。硐室几何形状、避灾人员分布及3台一体机位置如图1 所示。采用Tet／Hybrid进行体网格划分。划分后网格节点573809个，面网格6304053个，体网格3097324个。

图1 避难硐室物理简化模型

避难硐室模型涉及流体与固体两个区域，实体物为空气、岩体、人体面、空调面。根据大部分工程实例，选围岩类性为砂岩，密度2400kg／m3、比热920J／ （kg·K）、导热系数2 W／ （m·K），空调表面为钢。

在升温阶段，一体机仅为硐室内提供空气净化循环动力，不对硐室内降温。为避免一体机进出口温度不同，对室内热负荷造成影响，通过编制UDF程序控制一体机出风口温度，使一体机出风口温度等于其进风口的平均温度。考虑到室内空气温度变化对空气密度带来的影响，空气密度采用boussinesq假设。采用SIMPLE 算法进行计算，时间步长为1s。当硐室内平均温度上升到34℃（307.16K）后，停止升温阶段的计算。改变相应参数，进入恒温阶段模拟计算。升温阶段主要初始参数设置如表1所示。

升温阶段结束时的围岩温度条件即为恒温阶段的初始围岩边界条件，因此，在恒温阶段，不改变围岩参数，将人体表面设置为绝热面，将流体温度及一体机风口温度设为34℃，一体机风速仍为12 m／s。仍采用SIMPLE算法进行计算，改时间步长为5s，计算截止两个阶段的时间总长度为96h。

表1 主要初始参数设置

3.2 模拟计算结果分析

3.2.1 升温阶段一体机进、出口温度分析

取中间1台一体机的进、出口温度变化曲线进行分析，如图2、图3所示。

图2 进口温度曲线

图3 出口温度曲线

由图2和图3可以看出，通过UDF 程序控制的一体机进出、口温度随时间变化基本保持一致，能保证室内热负荷不受进出、口风流的影响，即一体机只具有空气净化功能。

3.2.2 升温阶段室内温度变化分析

通过Fluent每5 min记录一次室内平均空气温度，得出空气温度变化曲线如图4所示。经计算得出室内升温期空气温度变化曲线如图5所示。

图4 硐室内平均温度模拟计算曲线

图5 硐室内平均温度理论计算曲线

室内平均空气温度与进、出口空气温度具有相同的变化趋势。在经历1h的快速升温后，室内空气平均温度达到307.47K。而此后5h内温度上升缓慢。由图4 与图5 比较可看出，采用Fluent软件模拟与采用本文推导出的公式计算获得的温度曲线基本保持良好的一致性。

由Fluent中监视画面得出，经历5.56h 后，室内空气平均温度达到307.16K。5.56h后的空气温度场分布如图6所示，可看出，此时室内空气温度分布主要集中在306.5～308.5K 范围内。

图6 5.56h后硐室内温度场分布

3.2.3 热流密度分析

取硐室上下及左右两侧的围岩表面的热流密度进行分析，通过监视画面获得的热流密度曲线如图7所示。

图7 硐室围岩表面热流密度曲线

由图7可以看出，在升温期，室内空气与壁面非稳态耦合传热未达到动态传热平衡前，壁面的热流密度随空气与壁面温差的增大而增大，而达到传热动态平衡后，壁面的热流密度则相对比较稳定。恒温使用期，由于壁面的温度不断升高，室内空气与壁面的温差逐渐减小，因而壁面的平均热流密度随时间也不断降低。经计算可得恒温期壁面平均热流密度随时间变化曲线如图8所示。

图8 恒温期壁面平均热流密度曲线

通过图7与图8比较可以看出，计算得出的结果与采用Fluent模拟软件模拟计算得到的恒温期壁面热流密度随时间具有相同的变化趋势。经计算得到恒温传热90h 后的壁面热流密度为14.34 W／m2，而由Fluent软件计算得出恒温传热持续90h后的壁面平均热流密度为14.28 W／m2，采用两种方式计算得到的平均热流密度值相差较小。

图9 恒温传热90h后围岩温度场分布

3.2.4 岩体调热圈半径分析

通过在Fluent软件分析得出恒温90h后的围岩温度场分布如图9所示。

模拟计算得出，恒温90h后硐室壁面受传热影响的范围为1.98m，计算得出90h内围岩调热圈半径为2.15m。

4 总结

（1）结合避难硐室内是否采取降温措施及室内温度变化情况，将室内围岩结构与空气耦合传热问题划分为升温期与恒温期两个阶段。

（2）采用半无限物体传热理论，推导出硐室内恒温期围岩与空气耦合传热过程中热流密度计算公式。

（3）结合51人型避难硐室案例，利用Fluent软件对避难硐室内升温期和恒温期的传热过程进行分析，并与理论计算结果进行比较，相互验证了理论推导与数值计算的可靠性。

［1］ 李树荣，王洪权，王旭.矿井紧急避险设施设计与应用探讨 ［J］.中国煤炭，2012 （7）

［2］ 栗婧，金龙哲，汪声等.矿井密闭空间中人体呼吸商计算 ［J］.北京科技大学学报，2010 （8）

［3］ 王普秀.航天环境控制与生命保障工程基础 ［M］.北京：国防工业出版社，2003

［4］ 茅靳丰，韩旭.地下工程热湿理论与应用 ［M］.北京：中国建筑工业出版社，2009

［5］ 黄福其，张家猷.地下工程热工计算方法 ［M］.北京：中国建筑工业出版社，1981

［6］ 陶文铨.传热学 ［M］.西安：西北工业大学出版社，2006

［7］ 张祖敬，陈于金.煤矿避难硐室热环境控制范围探讨 ［J］.矿业安全与环保，2014 （1）