基于子空间类法的阵列误差有源校正方法

(电子科技大学电子工程学院,四川成都611731)

0 引言

对阵列误差的低鲁棒性,一直以来都是高分辨空间谱估计技术走向实用化的一个瓶颈[1],所以准确估计阵列误差、提高测角精度是国内外学者研究的热点[2-5]。现有的阵列校正方法通常可以分为自校正类[6]和有源校正类[7]。自校正类方法通常根据某种优化函数对空间信源的方位与阵列的扰动参数进行联合估计,阵列自校正可以不需要方位已知的辅助信源,而且可以在实际方位估计时在线完成。但是,信源方位和阵列误差参数之间往往相互耦合,使得自校正中参数估计的可辨识性很难得到保证[8]。有源校正通过在空间设置方位精确已知的辅助信源来对阵列扰动参数进行离线估计,本文主要讨论有源校正方法。

现有的有源校正算法很多,但是针对同时存在多种阵列误差的校正算法还比较少。文献[6]利用信号子空间和噪声子空间的正交性,提出了同时对通道幅度相位参数、阵元间互耦参数和入射角参数进行估计的自校正方法,但该方法需要对通道幅度相位参数、阵元间互耦参数的初值进行精确的估计。文献[9]提出了一种针对均匀线阵中互耦误差、阵元幅相误差、位置误差和多普勒频率估计方法,但实际中目标方位信息未知,所以存在目标方位和阵列误差参数之间的耦合,使得校正中参数估计的可辨识性降低。

本文提出了一种同时估计阵列位置参数、阵元幅相参数及阵元互耦参数的方法。该方法采用单个校正源,通过旋转阵列天线得到多个校正方位的样本数据,从而达到多个信源独立分时校正的效果;利用特征分解,得到信源导向矢量的估计值,根据信号空间和噪声空间的正交性得到代价函数,循环迭代估计出阵列位置参数、阵元幅相参数及阵元互耦参数。利用本文所提算法可以对同时校正多种阵列误差,通过计算机模拟仿真和实际阵列天线的校正实验均验证了该算法的性能。

1 信号模型及处理

M个阵元的均匀线阵,阵元间距d为半波长,在阵元远场中,信号源在以线阵法线为参考的θ处。以第一个阵元为参考阵元,假设理想的阵元位置为((i-1)d,0)(i=1,2,…,M)。接收到的快拍数据可以表示为

式中,S(t)为发射信号复包络;N(t)为M×1阵列 噪 声 矢 量;a0(θ)=[1,…,ex p(-iφ0m),…,exp(-iφ0M)](m=1,…,M)为阵列接收导向矢量,其中;K为快拍数。

阵列的协方差矩阵R定义为

式中,Rs=E[S(t)SH(t)]为信号源的协方差矩阵,I为单位矩阵,σ2为噪声功率。

考虑阵列误差时,接收到的快拍数据可以表示为

式中,互耦矩阵C为M×M维由阵元间互耦引入的误差矩阵,均匀线阵的互耦矩阵是Toeplitz阵;G=diag[1,g2exp(iφ2),…,g Mexp(iφM)]为阵元的 幅 相 误 差;a(θ)=[1,…,exp(-iφm),…,ex p(-iφM)]T,其中,[d1,d2,…,d M]为阵元的实际位置,且满足d i=(i-1)d+Δd i,Δd i为第i个阵元的位置扰动。

则阵列的协方差矩阵为

2 参数估计算法

对R进行特征分解得到：

式中,λ1为最大特征值。由子空间原理可知,归一化信号源导向矢量的估计值,其中e1为R的最大特征值对应的特征矢量,e11为e的第一个元素。定义E M=[e2,e3,…,e M],其各列张成噪声子空间,且与阵列流型张成的空间正交。

由信号空间和噪声空间的正交性,可以构造代价函数为Q=arH(θ)E M(E M)Har(θ),当ar(θ)为真实的阵列导向矢量(或者ar(θ)很接近真实导向矢量)时,代价函数Q取得最小值。基于时空矩阵特征分解的基本原理,采用迭代算法估计阵列误差参数。算法具体原理和步骤如下：

① 令循环次数r=0,给定C的初始值C0(一般取为单位矩阵I)。

② 天线阵列处在可精密旋转的转台上,转动线阵天线阵列,使天线连续转动J个角度θj(j=1,…,J)(利用多次的数据可更准确地估计阵列误差参数,尤其是在求阵列位置误差参数时可利用最小二乘估计),获得每个角度的样本数据,根据式(4)计算协方差矩阵R j,并将R j进行特征分解估计

将R j(j=1,…,J)分别进行特征分解得到最大特征值对应的归一化特征矢量构成areal(θj)。a m_real(θj)为areal(θj)的第m个元素,由式(4)可得

显然,各阵元的幅度因子[9]为

将式(7)两边取相位,由于函数exp(·)的周期性,存在相位模糊问题,则

记p(θj)=[arg(a1_real(θj)),…,arg(a M_real(θj))]T,c(θj)=[c1(θj),c2(θj),…,c M(θj)]T,φ =[φ1,φ2,…,φM]T,d=[d1,d2,…,d M]T,则由式(9)得

由式(10)可得

式中,c′(θj)=[c′1(θj),…,c′M(θj)]T=c(θj+1)-c(θj)亦为整数组成的列向量,记

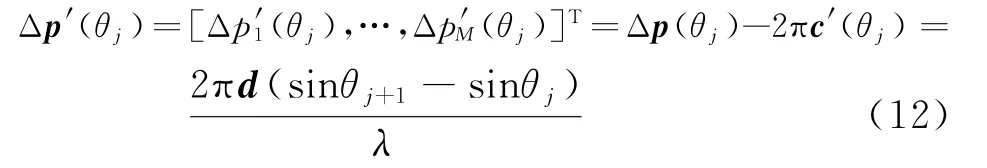
在阵元位置误差不太大时,对于均匀线阵,d1,d2,…,d M近似为线性变化,选取合适的c′(θj),使Δp′m(θj)满足近似线性变化。c′m(θj)的选取采用如下方法：

由于第一个阵元为参考阵元,p1(θj)=arg(a1_real(θj))=0,φ1=0,由式(9)可推知c′1(θj)=0。

对m＞2,c′m(θj)=-round[(m=3,4,…,M;j=1,2,…,J-1),round[x]等于最接近x的整数。

由式(12)可得

记为Y=B·X,其中Y=[Δp′(θ1),…,Δp′(θJ-1)],,X=[sinθ2-sinθ1,…,sinθJ-sinθJ-1]。

上式中Δp′(θj)是测量值,θj是已知值,则可以解出d。当J=3时,式(13)有唯一解,当J＞3时,式(13)为超定方程,其最小二乘解为B=YXT(XXT)-1。

阵元位置由下式估计：

将上式代回到式(10),则可由θj方向的数据估计出阵元的相位：

由式(15)可知,相位模糊不影响阵列天线相位φ的校正,即可写为

最后用J个φj的平均值来估计相位φ,即

④ 由信号空间和噪声空间的正交性,构造代价函数：

根据文献[5],若C为Toeplitz阵,式(18)可以写为

式中,c=C1k(k=1,2,…,L),L为C的第一行非零元素个数;M×L维矩阵T j=T1j+T2j,

如果限制c的第一个元素为1,即对c加上一个约束条件cHw=1(w=[1,0,0,…,0]T),采用拉格朗日乘子法在cHw=1的条件下使代价函数Q j取得最小值,可得到c的估计式：

式中,F j=THj E jM(E jM)HT j为L×L维矩阵。为提高精度,可由J次估计的的均值作为最后估计的,再由得到C r+1。

⑤ 计算总的代价函数为

当|Q r-Q r+1|＞ε(事先设定的门限),令r=r+1,转到③继续循环,否则循环结束。

3 仿真验证

为了验证上述方法的正确性,进行了相应的算法仿真,仿真条件：采用8阵元均匀线阵,d=[0,1.20,1.90,3.20,4.23,4.69,5.88,7.11],g=[1,1.3,0.7,1.1,1.2,0.8,1.2,0.7],φ=[0°,80.21°,-34.38°,5.73°,-51.57°,36.67°,8.02°,-22.92°],c=[1.000 0,-0.127 4-0.357 7i,0.3521+0.4001i],天线阵列转动角度分别为20°,40°,60°,80°,ε=1×10-9,信噪比SNR=20 dB。

图1给出了仿真校正的代价函数随循环次数变化曲线,由图可见,本方法是收敛的,代价函数随着循环次数的增加而逐渐减小,在循环开始时收敛速度较快,循环30次以后逐渐变慢,最后收敛到稳定值。表1、表2为计算机仿真校正结果,从表1、表2可以看出,本文所提算法可以很好地校正阵列误差,包括阵元幅相误差、阵列位置误差和阵元互耦误差。校正得到的估计值与阵列误差参数的真实值基本吻合。]

图1 仿真校正代价函数随迭代次数的变化曲线

表1 阵元位置、幅相误差的计算机仿真校正结果

表2 互耦系数的计算机仿真校正结果

4 实验验证

实际阵列天线处于可精密旋转的转台上,为8阵元均匀线阵,阵元间距为0.028 3 m(标称值),在天线阵列200 m以外有一信源发射C波段正弦波信号,天线阵列转动角度分别为-30°,0°,30°,ε=1×10-9信噪比约为30 dB。

图2给出了实际天线阵列校正的代价函数随循环次数变化曲线,由图可见,跟仿真实验结果一致,该校正方法是收敛的,代价函数随着循环次数的增加而逐渐减小,在循环开始时收敛速度较快,循环4次以后逐渐变慢,最后收敛到稳定值。由于影响实际天线阵列校正的因素较多,例如天气、地面环境等,所以代价函数最后收敛的稳定值比仿真校正时的稳定值大。

图2 实验校正代价函数随迭代次数的变化曲线

表3、表4为实际天线阵列各阵列误差参数的校正结果,把校正得到的误差参数补偿到阵列接收数据中,再进行MUSIC谱估计,就可以消除阵列误差对MUSIC谱估计的影响了。

表3 实际天线阵列互耦系数校正结果

表4 实际天线阵列阵元位置、幅相误差校正结果

图3是实际天线阵列误差校正前后MUSIC谱估计的对比关系图。从图中可以看出,存在阵列误差的情况下,MUSIC算法的旁瓣电平很高,而且峰值严重偏离了真实的来波方向。采用本文所提的迭代方法对阵列误差进行校正,再进行MUSIC处理,从图中可以看出,阵列误差校正后的谱峰已经相当尖锐,旁瓣电平比未校正时低了很多,而且峰值出现的位置基本与来波方向一致。

5 结束语

本文基于时空矩阵特征分解的基本原理,提出了采用迭代算法同时估计阵列位置参数、阵元幅相参数及阵元互耦参数的方法。考虑了各种误差同时存在的情况,更符合实际应用背景。仿真和实测数据验证了本文所提方法收敛性能好。由仿真数据校正得到的阵列误差参数的估计值与真实值基本吻合,说明该方法误差参数校正的精度高。并对比了实测数据阵列误差校正前后的MUSIC谱,阵列误差校正后的MUSIC谱峰更尖锐,旁瓣更低,DOA估计精度大大提高。所以该方法的实用性很高,可用于实际系统阵列误差的校正。

图3 阵列误差校正前后的MUSIC谱对比

[1]FRIEDLANDER B.A Sensitivity Analysis of the MUSIC Algorithm[J].IEEE Trans on ASSP,1990,38(10)：1740-1751.

[2]唐雪峰,胡晓琴,花良发,等.基于辅助阵元的十字阵阵元位置误差校正方法[J].现代雷达,2013,35(9)：77-79.

[3]陈之涛,王雨阳,刘浩.一种发射通道校正技术的实现[J].雷达科学与技术,2012,10(3)：332-335.CHEN Zhi-tao,WANG Yu-yang,LIU Hao.An Implementation of Calibration Method for Transmitting Channels[J].Radar Science and Technology,2012,10(3)：332-335.(in Chinese)

[4]WANG Guibao,TAO Haihong,SU Jia,et al.Mutual Coupling Calibration for Electromagnetic Vector Sensor Array[C]//2012 10th International Symposium on Antennas,Propagation&EM Theory,Xi’an,China：[s.n.],2012：261-264.

[5]郑志东,张剑云,康凯,等.互耦条件下双基地MIMO雷达的收发角度估计[J].中国科学：信息科学,2013,43(6)：784-797.

[6]FRIEDLANDER B,WEISS A J.Direction Finding in the Presence of Mutual Coupling[J].IEEE Trans on AP,1991,39(3)：273-284.

[7]刘洛琨,王鼎,汪涛.抑制校正源方位偏差的阵列误差矩阵鲁棒校正算法[J].系统工程与电子技术,2014,36(3)：409-416.

[8]ASZTELY D,SWINDLEHURST A,OTTERSTEN B.Spatial Signature Estimation for Uniform Linear Arrays with Unknown Receiver Gains and Phases[J].IEEE Trans on Signal Processing,1999,47(8)：2128-2138.

[9]李琼,叶中付,徐旭.存在阵列误差条件下的目标二维参数估计[J].中国科学技术大学学报,2004,34(4)：487-494.