基于捷变频非合作雷达辐射源的无源雷达时频同步方法

(国防科技大学自动目标识别重点实验室,湖南长沙410073)

0 引言

无源雷达[1]自身不发射电磁波,而是用第三方辐射源信号作为参考信号来探测目标,具有优越的“四抗”特性。对于非合作雷达辐射源的无源雷达探测系统,无源雷达必须通过空间和频率搜索来截获非合作雷达辐射源的直达波信号,根据搜索时记录的射频频率值来完成频率同步,再从直达波提取发射脉冲前沿来完成时间同步。因此,对于无源雷达探测系统,时间同步、频率同步的关键在于直达波参数的提取。

如何快速、准确地提取直达波参数来实现时间、频率同步一直是无源雷达技术的难点之一。本文研究的直达波为线性调频(LFM)信号,估计的参数有脉冲到达时间(TOA)、脉宽(PW)、带宽、载频(CF)。针对LFM信号检测问题,目前已有众多文献提出了许多应用于不同场合的检测算法,包括分数阶傅里叶变换(FFT)、魏格纳分布(WVD)、最大似然估计(MLE)、短时傅里叶变换(STFT)、小波变换(WT)等方法。文献[2]提出了用FRFT插值实现LFM信号的参数估计方法,突破了分数阶傅里叶域分辨率的限制,提高了参数估计的精度。文献[3]借助 WVD-Hough变换的线性积分过程实现LFM信号的检测与参数估计。文献[4]提出了用MLE方法估计跳频信号的载频及跳频时间周期。文献[5]提出了基于短时傅里叶变换和小波变换的参数估计算法,然而STFT窄的观察窗和WT宽度变换的时间窗影响了时频域的分辨率。

为了将算法应用于工程,必须寻找一种能够快速估计参数的方法,本文用分段自相关法[6]粗略估计脉宽和脉冲到达时间,该方法计算量小、精度较高,粗略估计的脉宽与精确参数模板匹配后可以获得精确的脉宽参数。针对某捷变频雷达信号特点,采用改进的解线调方法[7]估计带宽和载频,该方法能够准确估计出带宽的值,且粗略估计的载频与精确参数模板匹配后可以获得精确的载频参数。通过匹配滤波[8]的方法精确估计脉冲到达时间的值。本文提出的快速估计某捷变频雷达直达波信号参数的方法计算量小、精度高,适合实际工程实现。

1 脉冲参数提取的流程及算法介绍

本节主要介绍脉冲参数提取的流程及算法,流程如下：

首先,用分段自相关方法粗略估计脉宽和脉冲到达时间,通过与脉宽模板匹配,获得脉宽的精确值;其次,用解线调的方法精确估计带宽、粗略估计载频,通过与载频模板匹配,获得载频的精确值;最后,利用精确的脉宽、载频、带宽,用匹配滤波的方法精确估计脉冲的到达时间,进而实现时频同步,流程图如图1所示。

下面介绍参数提取流程中所需要用到的算法。

1.1 分段自相关法估计脉宽及脉冲到达时间

设实际接收到的信号为

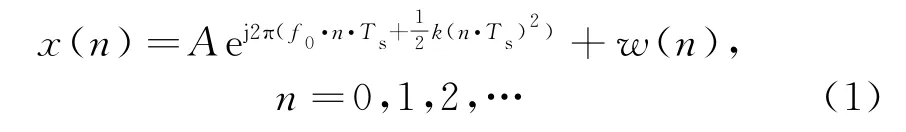
式中,A,f0,k分别为LFM信号的幅度、起始频率和调频斜率;Ts为采样间隔;w(n)为均值为零、方差为σ2的高斯白噪声。分段自相关法[6]的相关函数为

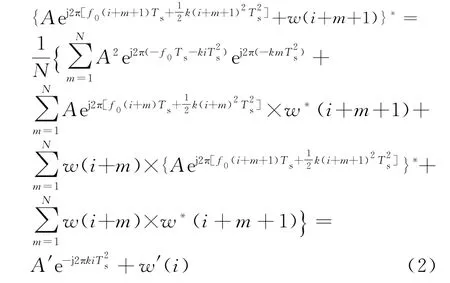
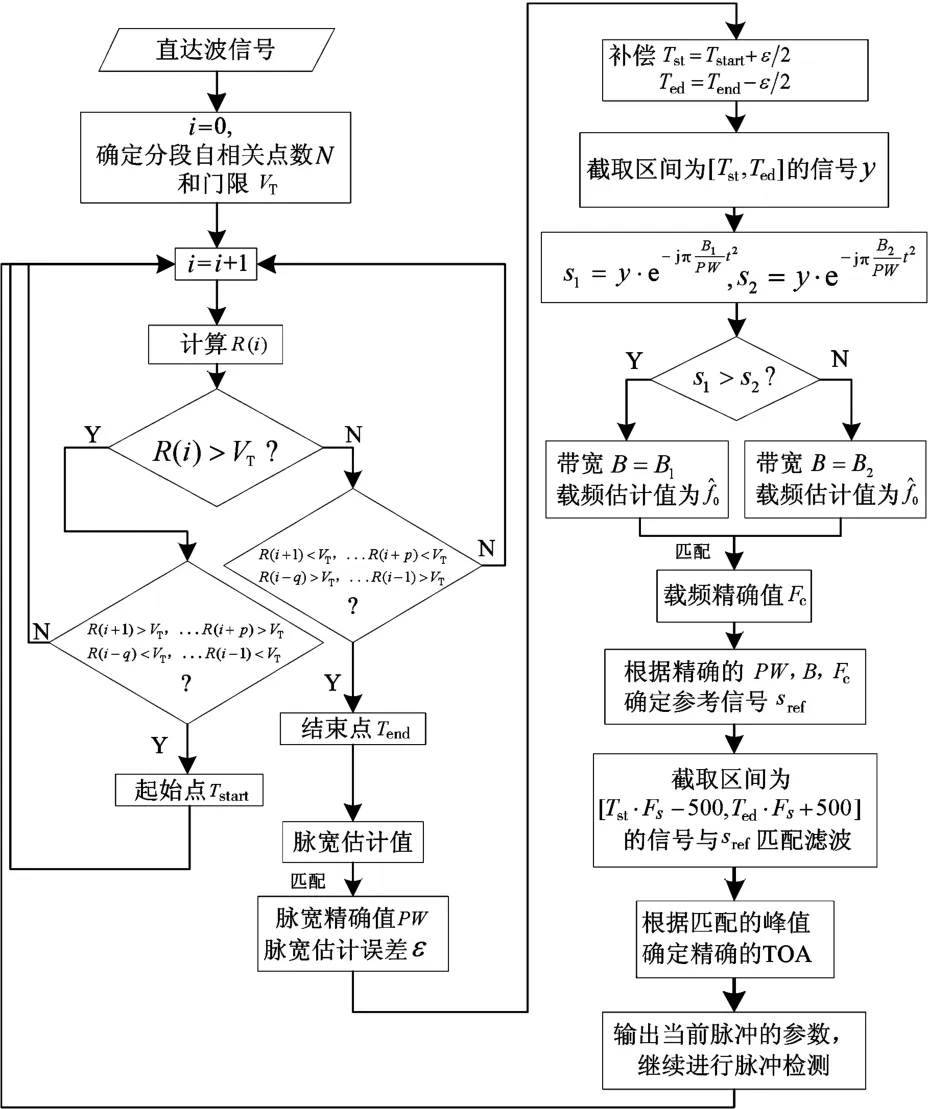
图1 参数估计流程图

式中,w′(i)为相关后的噪声,A′e-j2πkiT2s为信号部分,且

当积累点数N较大时,根据中心极限定理,w′(i)可以看作为均值为0,方差为的高斯白噪声。

该算法可由下式进行迭代运算：

从式(3)可以看出,采用这种递推的计算方法,每计算一个R(i)仅需要一次复数乘法和一次复数加法,计算量大大减少,因此适合硬件实时处理。

1.1.1 检测门限确定

为了检测是否存在脉冲信号,需要确定检测门限,而检测门限应随噪声的变化而变化,所以需要估计噪声的方差,噪声的标准差的无偏估计值σ由下式决定：

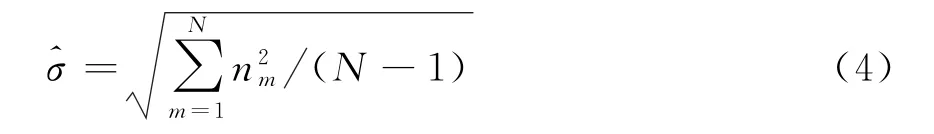
式中,n m为第m时刻的噪声值。

无信号时,R(i)的实部、虚部的噪声相互独立,都服从N(0,σ2/2N)分布,则R(i)的模值服从均值,方差的瑞利分布。因此,在一定的虚警概率条件下,本文取检测门限

式中,a由虚警概率确定。

确定检测门限以后,大于VT的部分即认为有信号,反之没有信号,但是由于噪声的随机性,在没有信号的情况下,可能会出现虚警;当信号较弱时,可能会出现漏警。为了消除这种影响,采用双门限法,即认为只有当连续超过门限p次,才认为有信号,同理,只有连续低于门限q次,才认为信号结束。

由于相关运算的延迟效应,相关后的结果近似为一个梯形,图2中实线代表自相关运算结果,AC=DF=N,H、F为信号的真实起止点,G、J为检测到的起止点,则脉冲起点修正值为,终止点的修正值为,其中,BG=EJ=VT,CH、BG为梯形高度估计值。

图2 分段自相关检测示意图

1.1.2 分段自相关法估计脉宽、脉冲到达时间的步骤

首先给出以下两个定义：

① 脉冲检测状态 上一个脉冲结束与下一个脉冲到达之间的系统状态;

② 脉冲测量状态 同一个脉冲到达与结束之间的系统状态。

分段自相关算法描述如下：

Step1 以信号第一个点为起点截取长度为N的序列,记为x(1),以信号第二个点为起点截取长度为N的序列,记为x(2),依次类推。N≪n,n为一个调频周期内信号序列长度。

Step2 利用式(2)和式(3)计算R(i)。

Step3 设定检测门限VT,如果R(i)＜VT且系统处于脉冲检测状态,则重复Step2和Step3,如果R(i)＜VT且系统处于脉冲测量状态,则转入Step5;如果R(i)＞VT,则转入Step4。

Step4 记录当前对应的时间Tstart,则为脉冲到达时间的估计。

Step5 判断脉冲是否结束。如果结束,则记录当前对应时间Tend。

1.2 解线调法估计载频

解线调就是解除线性调频信号s(n)的线性调制,将s(n)变成一个单频信号,然后测得该单频信号的频率,即线性调频信号的载频。

令s(n)为一个单分量线性调频信号：s(n)=,n=0,1,2,…,假定s(n)的调频

斜率k已知,用e-j2πk(nTs)2与信号相乘,得

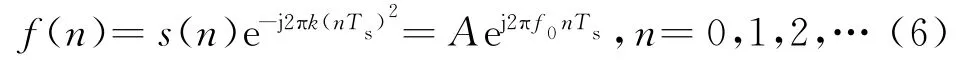
即f(n)变成了单频信号,其频率等于起始频率f0。

假设测得信号s(n)的脉冲到达时间为Tstart,脉冲结束时间为Tend,脉宽为PW,经精确脉宽模板匹配后得信号的脉宽为T,而Tstart,Tend修正为,截取区间为的一段信号进一步处理,因为实测数据带宽有两种,分别为B1,B2,所以,调频斜率有两种,分别为,利用式(6),得

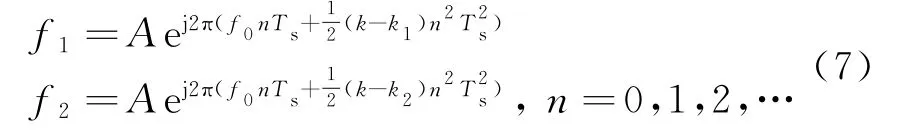
对于单频信号,能量聚集在一个频点上,而对于LFM信号,能量则分布于整个带宽上,因此,通过测量比较f1,f2频谱的最大值,便可以得到精确的线性调频斜率k,进而得到信号的带宽B,同时通过单频信号的频谱也可以估计出信号的载频0。再与精确载频模板匹配,可以得到精确的载频f0。

1.3 匹配滤波法精确估计脉冲到达时间

由于分段自相关算法估计脉冲到达时间存在误差,这将影响后期雷达测距时的精度,因此,有必要再进一步提高脉冲到达时间的精度。本文采用匹配滤波方法。

已知某个输入信号x′(t)同时包含目标x(t)和噪声分量ω(t),则滤波器的输出由卷积给出：

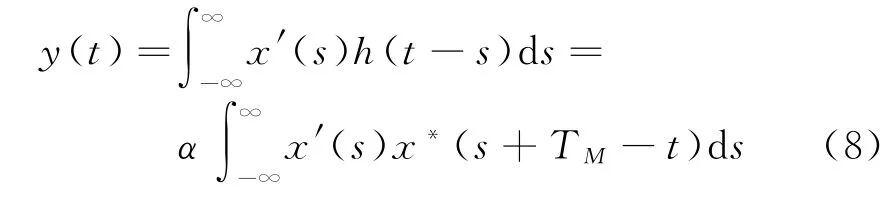
式中,h(t)为匹配滤波器的冲击响应,且h(t)=αx∗(T M-t),由上式可知,匹配滤波器的输出端在t=T M时取得峰值。

通过分段自相关法和解线调法可以粗略估计脉冲的脉宽、载频,经过与精确参数模板匹配,便可以精确得到脉冲的脉宽T、带宽B、载频f0,在得到信号的精确参数后,重构原始信号Sref=,1≤n≤T∗Fs,假设通过自相关法测得的脉冲到达时间为Tstart,脉冲结束时间为Tend,则截取宽度为[Tstart-500/Fs,Tend+500/Fs]的一段信号s′(n),使s′(n)包含原始信号,通过s′(n)与Sref匹配后的输出最大值点的位置,则可以得到精确的脉冲到达时间。

2 仿真试验与算法性能分析

本文研究的对象为非合作雷达辐射源,信号参数是通过长期侦察获取的,由于对方的雷达参数未知,本文假定获取的信号参数是正确的,并作为精确参数模板来实现时频同步。因此,本文不研究如何获取参数模板及参数模板的误差等问题。

为了验证本文算法的有效性,将进行3组仿真试验,分别验证不同的脉宽、带宽、载频对本文算法的影响。

(1)仿真1 本文方法对不同脉宽的信号进行参数估计。

产生四组线性调频信号,带宽为0.25 M Hz,载频为20 M Hz,脉宽分别为50μs,200μs,1 ms,4.5 ms,采样率fs=62.5 M Hz,TOA=0.1 ms,进行500次Monte-Carlo仿真。

对输入信号加不同信噪比的噪声。通过分段自相关法和解线调法估计信号的脉宽、载频、脉冲到达时间。仿真结果如图3所示。

通过图3(a)可以看出,分段自相关方法估计脉宽所产生的误差随信噪比的增大而减小,当信噪比大于15 dB时,误差趋近于定值,对四种不同脉宽信号,当信噪比大于10 dB时,脉宽误差在0.15μs以内,可以通过精确的脉宽模板得到精确的脉宽参数。

从图3(b)可以看出,解线调方法估计信号载频所产生的误差受信噪比的影响较小,且误差在10 k Hz以内,可以通过精确的载频模板得到载频参数。通过图3(c)可以看出,本文方法能够精确估计出带宽参数。通过图3(d)可以看出,通过匹配滤波法估计脉冲到达时间,抗噪性较好,对四种脉冲信号,当信噪比大于5 d B时,误差在0.05μs以内。

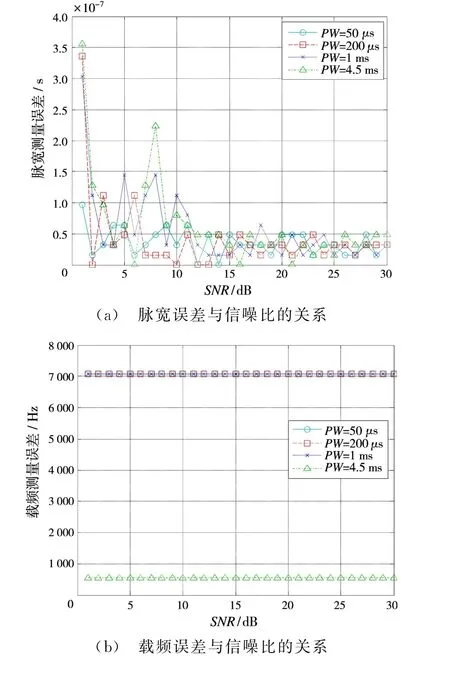
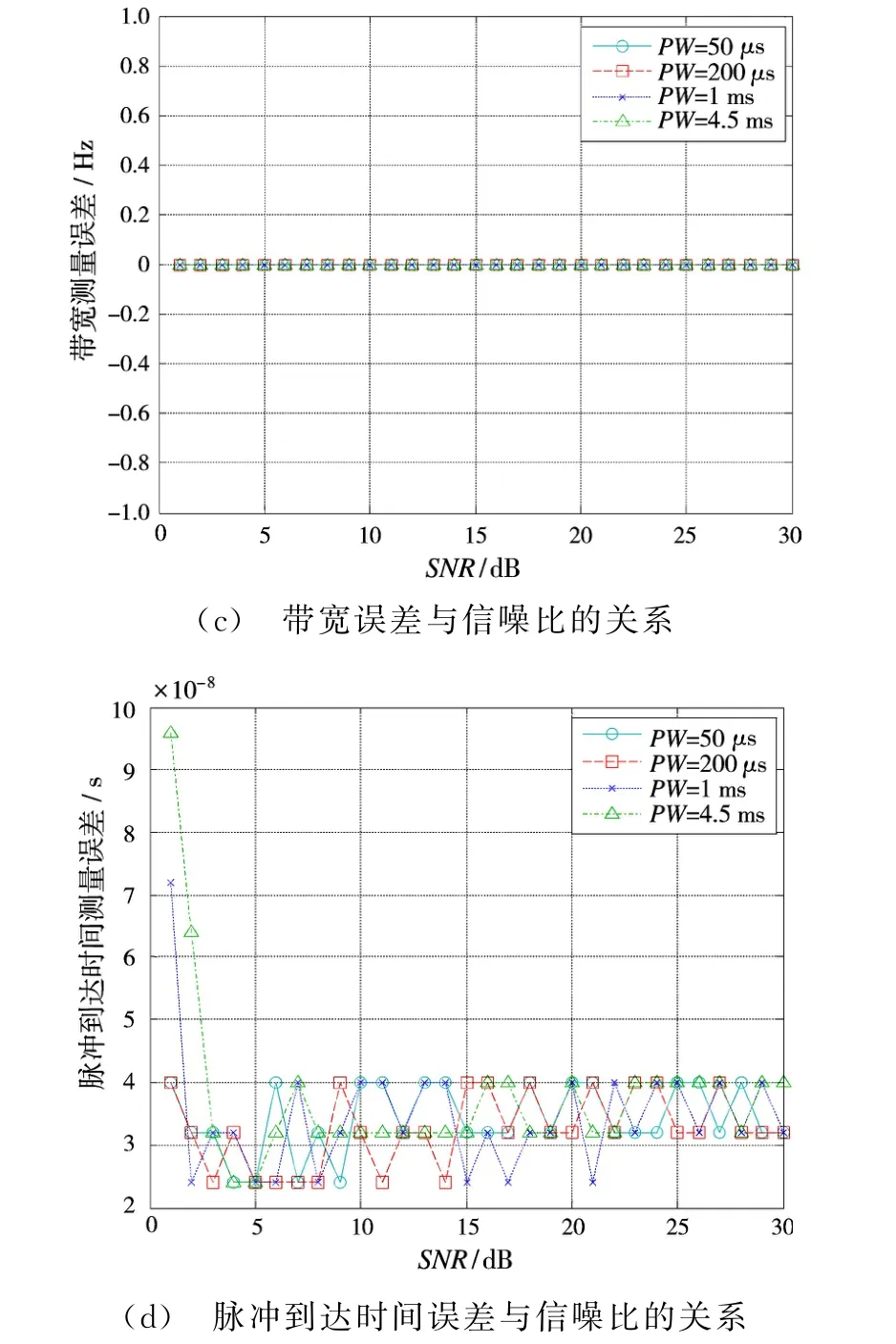
图3 不同脉宽下参数估计误差与信噪比的关系

(2)仿真2 本文方法对不同带宽的信号进行参数估计

产生四组线性调频信号,脉宽为200μs,载频为20 MHz,带宽分别为0.25,1,1.5和2 MHz,采样率fs=62.5 M Hz,TOA=0.1 ms,进行500次Monte-Carlo仿真。

对输入信号加不同信噪比的噪声。通过分段自相关法和解线调法估计信号的脉宽、载频、脉冲到达时间。仿真结果如图4所示。

从图4可以看出,仿真2的结果与仿真1的结果近似,在信噪比大于10 d B时,脉宽估计误差小于0.1μs,带宽误差小于10 k Hz,脉冲到达时间小于0.05μs,误差都在允许范围之内。

(3)仿真3 本文方法对不同载频的信号进行参数估计

产生四组线性调频信号,脉宽为200μs,带宽为0.25 MHz,载频分别为-5,1.5,10和20 MHz,采样率fs=62.5 M Hz,TOA=0.1 ms,进行500次Monte-Carlo仿真。

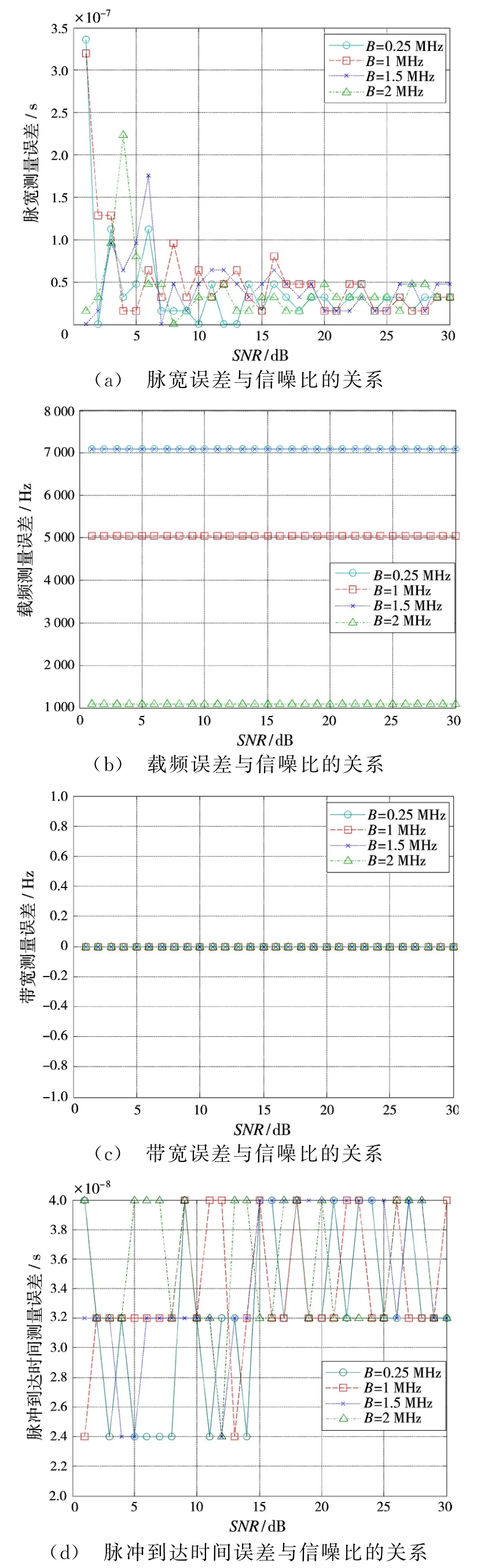
图4 不同带宽下参数估计误差与信噪比的关系

对输入信号加不同信噪比的噪声。通过分段自相关法和解线调法估计信号的脉宽、载频、脉冲到达时间。仿真结果如图5所示。

从图5可以看出,在信噪比大于10 dB时,脉宽估计误差小于0.1μs,载频误差小于10 k Hz,脉冲到达时间小于0.05μs,误差都在允许范围之内。

通过上面三个仿真实验可以得出,本文提出的方法受脉冲信号的脉宽、带宽、载频等因素影响较小,分段自相关方法估计脉宽的误差和解线调方法估计载频的误差都在允许范围之内,可以通过与精确参数模板匹配得到精确的脉宽及载频。用匹配的方法估计脉冲到达时间性能比较稳定,误差在0.05μs以内。

3 实测数据验证

实测数据来源于某捷变频雷达,通过长时间的分析实测数据,获得了该雷达发射脉冲的精确参数模板。根据本文提出的参数估计方法及流程,可快速、准确地估计出信号的脉宽、带宽、载频、脉冲到达时间。表1和表2列出了本文算法测得的部分参数与精确测量参数的对比,通过表格可以看出,本文方法可以精确地估计出实测数据的带宽,与仿真试验对比,脉宽和载频误差有所偏大,但是误差在允许范围之内,可以与精确参数模板匹配得到精确的脉宽和载频。最后通过匹配滤波方法估计的脉冲到达时间误差在1μs以内。

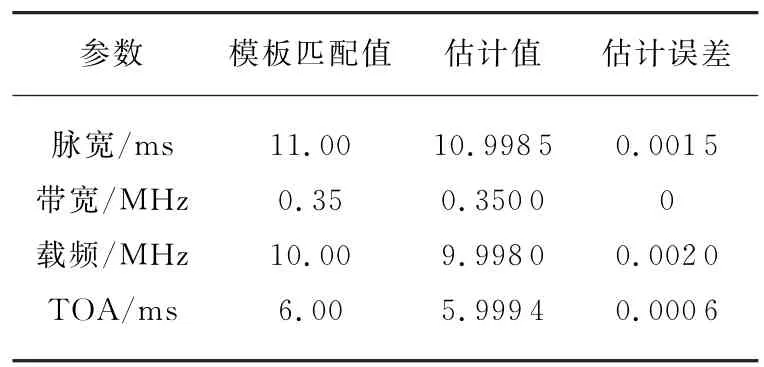
表1 脉宽为11 ms的脉冲

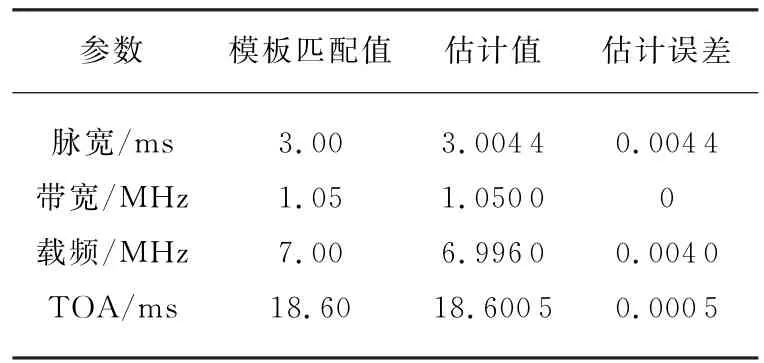
表2 脉宽为3 ms的脉冲

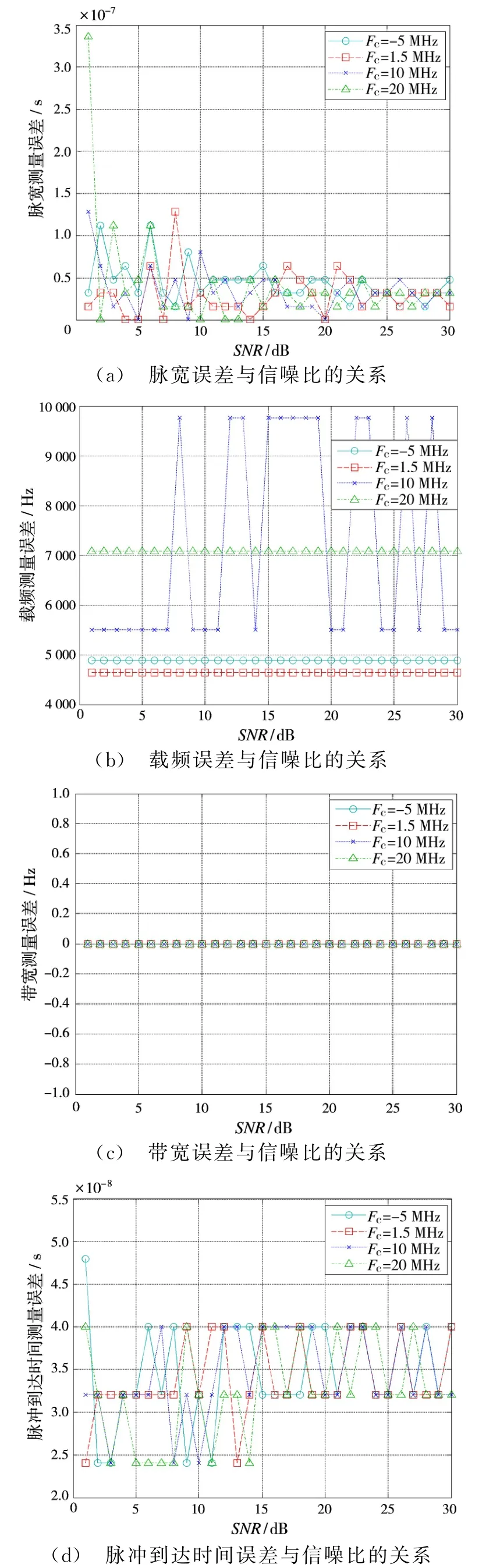
图5 不同载频下参数估计误差与信噪比的关系

4 结束语

本文针对某捷变频非合作无源雷达的直达波信号特性,提出了直达波参数提取方法及流程,实现了系统的时间同步和频率同步。本文先是通过仿真试验,验证了本文方法对不同脉冲的有效性,接着对实测信号进行参数估计,结果表明,在有精确参数模板的条件下,分段自相关及解线调方法可以精确估计出脉宽、载频及带宽,匹配滤波方法估计的TOA误差也在1μs以内,适合实际工程应用。

[1]宋杰,何友,蔡复青,等.基于非合作雷达辐射源的无源雷达技术综述[J].系统工程与电子技术,2009,31(9)：2151-2156.

[2]宋军,刘渝,朱霞.LFM信号参数估计的插值FRFT算法[J].系统工程与电子技术,2011,33(10)：2188-2193.

[3]BARBAROSSA S.Analysis of Multicomponent LFM Signals by a Combined Wigner-Hough Transform[J].IEEE Trans on Signal Processing,1995,43(6)：1511-1515.

[4]KO C C,ZHI W,CHIN F.ML-Based Frequency Estimation and Synchronization of Frequency Hopping Signals[J].IEEE Trans on Signal Processing,2005,53(2)：403-410.

[5]PERRY R P,DIPIETRO R C,FANTE R.SAR Imaging of Moving Targets[J].IEEE Trans on Aerospace and Electronic Systems,1999,35(1)：188-200.

[6]席轶敏,刘渝,靖晟.电子侦察信号实时检测算法及性能分析[J].南京航空航天大学学报,2001,33(3)：277-281.XI Yimin,LIU Yu,JING Sheng.Analysis on Probability of False Alarm and Detection[J].Journal of Nanjing University of Aeronautics&Astronautics,2001,33(3)：277-281.(in Chinese)

[7]XU X,FAN F,CAO B,et al.Parameter Estimation of LFM Signal Based on CAPON and One-Dimensional Dechirp[C]//TENCON 2003-2013 IEEE Region 10 Conference,Xi’an,China：IEEE,2013：1-4.

[8]刑孟道,王彤,李真芳,等.雷达信号处理基础[M].北京：电子工业出版社,2008：118-123.

[9]ITO T,TAKAHASHI R,MORITA S,et al.Experimental Result of Passive Bistatic Radar with Unknown Transmitting Radar Pulse[C]//2013 European Microwave Conference,[S.l.]：IEEE,2013：1767-1770.

[10]沈锐超,鲍庆龙,周成家,等.一种非合作双基地雷达空间同步定位精度[J].雷达科学与技术,2011,9(5)：393-396.SHEN Rui-chao,BAO Qing-long,ZHOU Chengjia,et al.Location Accuracy of Non-Cooperative Bistatic Radar Based on Spatial Synchronization[J].Radar Science and Technology,2011,9(5)：393-396.(in Chinese)

[11]SIMIN Z,DEGUO Z,BIN T.A Wideband Pulse Detection Algorithm Based on Autocorrelation[C]//9th International Conference on Electronic Measurement&Instruments,[S.l.]：IEEE,2009：4-287-4-289.

[12]CHAN Y T,LEE B H,INKOL R,et al.Estimation of Pulse Parameters by Autoconvolution and Least Squares[J].IEEE Trans on Aerospace and Electronic Systems,2010,46(1)：363-374.