谢桥矿坚硬顶板破断规律研究

袁晓龙，傅菊根，赵士兵

(1．安徽理工大学 土木建筑学院，安徽 淮南 232001；2．中煤矿山建设公司， 安徽 合肥 230000)

目前我国华东地区，浅部单一煤层接近枯竭，已进入深部、高地应力、高瓦斯复杂赋存条件下的煤层开采期[1]。在深部煤层开采过程中，坚硬顶板大面积悬顶突然垮落事故频发，对经济发展和人民生命财产造成了重大损失[2]。国内外学者一直十分重视坚硬顶板控制的研究，并且取得许多卓有成效的成果[2-4]。纵观这些研究可以发现，顶板的破断规律是这些研究开展的基础。

谢桥矿13216工作面倾斜长157.6m, 顶板为砂岩，厚度达6.8～19.6m，致密坚硬。已采工作面12228的砂岩厚硬顶板最大垮落步距76m，顶板突然来压，造成工作面支架活柱瞬间下缩，局部顶板垮落时形成飓风对人员安全及设备构成严重威胁，因此该矿坚硬顶板破断规律研究亟待进行。

1 极限垮落步距计算

厚硬顶板虽然也经历了成岩过程和构造运动，但宏观来看其具有硬、整、厚的特点，因此可近似地把同一层顶板看作连续介质建立计算模型。谢桥矿13216工作面煤层平均厚度2.7m，顶板为砂岩(岩石坚固性系数f=7～9)。初次来压前，两对边煤壁分别为工作面和开切眼的煤壁，另外两个对边则是实体煤壁。一般根据现场情况来看，大多数工作面的极限垮落步距大于工作面长度的1/2，厚硬顶板的厚度为4～8m，极限垮落步距为40～100m，综采工作面约长100～150m，坚硬顶板的厚宽比为1/5～1/80[5]，符合薄板理论。根据工作面实际开采情况和已有经验可知厚宽比为1/6.2，采场顶板简化为钱鸣高[6]提出的四周固支约束的薄板力学模型，且其受均布压力(如图1所示)。

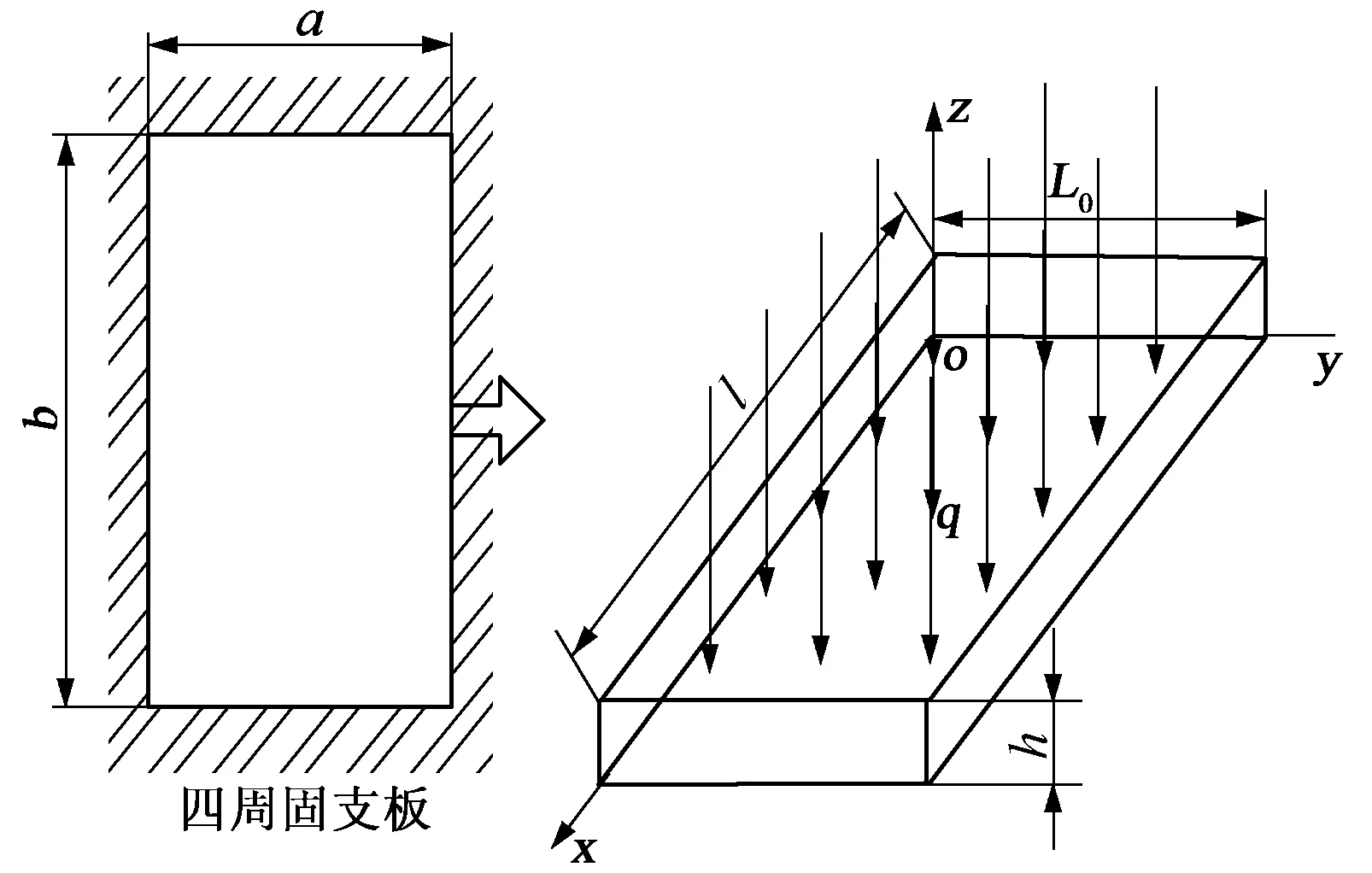
a—板的短边边长；b—板的场边边长；h—顶板的厚度；L0—顶板的极限垮落步距；l—工作面长度；q—板所承受的单位面积荷载(含自重)图1 顶板简化力学模型

根据板的Marcus算法，将板视为分条的梁，对中部来说即为交叉的条梁，按挠度相等的原则：

(1)

式中，qx,qy为板在x，y作为条梁时的单位长度荷载；Mx,My为板在长边、短边中部弯矩处的最大弯矩；q，l，L0同图1注释。

由于考虑到坚硬顶板上覆岩层对顶板的作用，所以岩板所承受的单位面积荷载(含自重)：

(2)

式中，q为板所承受的单位面积荷载(含自重)；E为岩梁本身的弹性模量；H为初次垮落的岩梁厚度；γ为岩层的容重；E1，E2，…，En为上覆各岩层的弹性模量；h1，h2，…，hn为上覆各岩层的厚度。

坚硬岩板及其上覆岩层荷载q=0.416MPa(其中岩石力学参数见表1)。

表1 岩体力学参数

四边固支岩板的弯矩分布[7]如图2所示，由弯矩图可以看出长边的中部弯矩最大，即工作面的中部。根据岩板的受力分析及岩石的破坏理论可知，岩板的破坏是由于岩石所受到的拉应力大于岩石的允许拉应力，即σmax≥[σ]。故以最大弯矩处的最大拉应力大于岩板的极限抗拉强度时为依据，计算岩板首先开裂时的跨距，即为极限垮落步距L0。根据已采工作面经验知L0≤l。

图2 四边固支岩板弯矩分布

当L0≤l时，岩板的最大弯矩简化为[8-9]：

(3)

此时的最大拉应力为：

(4)

当σmax=Rt时，取得最大跨距：

(5)

式(3)，(4)，(5)中，σmax为岩石承受的最大拉应力；Mmax为板承受的最大弯矩；H为基本顶岩层的单层厚度；Rt为岩石的极限抗拉强度；J为对中性轴的断面矩。

将q=0.416MPa，l=157m，H=16m，Rt=3.5MPa代入式(5)得顶板的极限垮落步距L0=88.2m。验证其厚宽比为1/5≥1/5.5≥1/80，采用岩板模型是正确的。

2 有限元数值模拟

2.1 数值计算参数

根据岩石力学试验结果：当载荷达到峰值强度后，岩石破坏，并在峰值之后产生塑性流动，岩体仍具有一定的承载能力。同时岩石在高应力三围应力环境下，岩石呈剪切破坏，莫尔强度理论较全面地反映了岩石的强度特性，它适用于塑性岩石以及脆性岩石的剪切破坏。因此，计算中采用莫尔-库伦屈服破坏准则，判断岩石的破坏,同时采用应变软化模型以正确合理地反映模拟塑性破坏区的变化特性 。根据室内试验和相关理论研究提供的岩石力学试验结果，考虑岩石的尺寸效应，模型模拟计算采用的主要岩石力学参数见表1。

采空区的垮落材料成块状，且块体之间空隙较大，局部是不连续且各向异性，但是宏观层面可以把垮落岩体看成弹性体，即采空区采用弹性模型进行模拟。模型顶部的竖向荷载可由13216工作面的标高(H=-462.0～-489.9m)和上覆岩层的平均密度(d=2500kg/m3)计算而得，经计算σz=-3.75MPa。考虑构造应力的影响，根据蔡美峰[10]、朱焕春[11]等的研究，煤体按照岩体考虑，在煤层的倾向的水平应力取竖直应力的1.25倍，沿煤层走向的水平应力取竖直应力的0.75倍。

2.2 数值计算中监测点布置

为研究坚硬顶板较薄煤层开采过程中，采场应力分布情况，在开切眼前方煤层中20m，60m，90m，120m，130m，150m处设置监测站，测点为顺层布置，测点距巷帮分布为75m，监测点距巷道底板高度为0.8m。监测整个开采过程中煤层受力变化，分析其应力集中程度，判别坚硬顶板极限垮落步距，模拟工作面回采300m，其监测点布置如图3所示。

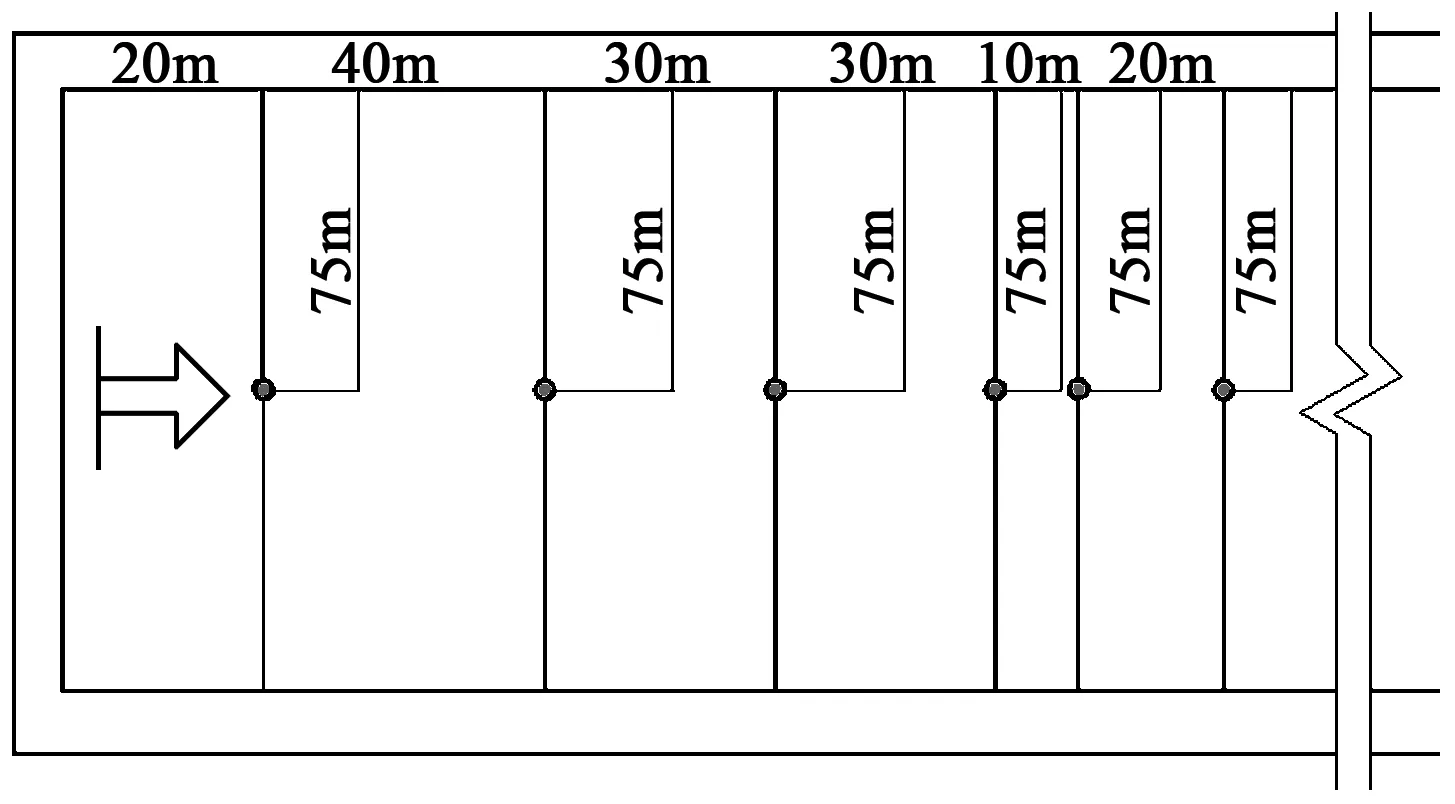
图3 采场应力测点布置

2.3 根据支承压力分布规律确定初次破断步距

工作面顶板初次断裂前，随工作面的推进，悬露的顶板长度增加，工作面支承压力增大。图4为不同推进距离工作面煤壁前方支承压力曲线。

图4 不同推进距离工作面煤壁前方支承压力

可以看出，随着工作面推进距离的增加，基本顶悬露的长度和面积增加，引起工作面煤壁前方煤层垂直应力峰值逐渐增加，但是随工作面推进引起煤体支承压力峰值的增加量逐渐变小，其变化趋势曲线趋于平缓。由图5可以看出曲线比较平缓段的分界点是85～90m。

图5 煤层走向支承压力峰值与推进距离关系

根据计算结果，工作面走向前方煤体中的支承应力σz与推进距离x的变化关系，可以用多项式函数分别表示。

σz= 5×10-6x3- 0.0031x2+0.5705x+19.34

式中，σz为工作面走向煤体支承压力峰值，MPa；x为推进距离，m。

图6为工作面煤层走向支承压力影响范围与推进距离的关系曲线，由图6可知，随着工作面推进距离的增加，工作面煤壁前方应力影响范围逐渐增加，但是工作面推进距离对支承压力影响范围的影响程度比压力峰值影响小。支承压力影响范围在推进距离为90m时达到最大值。由此可以判断工作面顶板初次来压步距在85～90m范围内。

图6 煤层走向支承压力影响范围与推进距离关系

工作面顶板初次断裂前，随工作面的推进，悬露的顶板长度增加，工作面顶板内应力增大；当工作面顶板断裂后，工作面顶板内应力下降。图7为工作面不同厚度上覆岩层下推进距离与支承压力关系曲线。

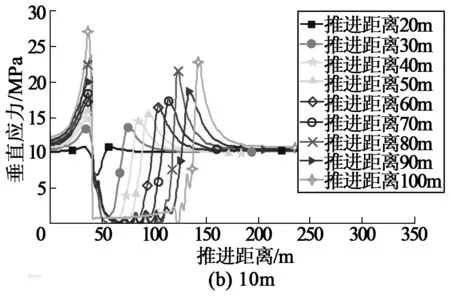
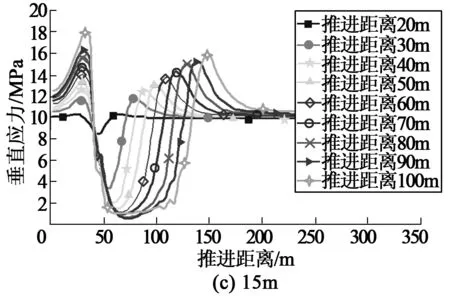
图7 不同上覆岩层推进距离与支承压力关系

由图7可以看出，随着工作面的推进，形成的悬露面积的增大，工作面上覆岩层原始应力重新分配，并在上覆岩层采空区对应空间两端形成高度的应力集中。在初次来压之前，上覆岩层沿走向可以看成两端固支梁，其两端会形成高度力矩和应力集中。不同层位上覆岩层的支承压力峰值与位置不一致，随着层位的增加，覆岩支承压力峰值降低，峰值位置距其工作面距离增大，但同一层位覆岩不同推进距离，峰值位置没有变化，说明推进距离对覆岩支承压力峰值位置没有影响，只有覆岩的层位对支承压力峰值位置有影响。

图8为不同层位上覆岩层支承压力峰值与推进距离的拟合曲线。由图8可知，随着工作面推进距离的增加，基本顶悬露的长度和面积增加，引起上覆岩层相对应的工作面煤壁前方支承压力峰值逐渐增加，但工作面推进单位距离引起煤体支承压力峰值的增加量逐渐变小，其变化趋势趋于平缓。在距煤层顶部10m层位的岩层，也就是工作面上方10m细砂岩与8m中砂岩的分界面处，当工作面推进到85m处，岩层上作用的支承压力峰值最大，达到21.6MPa，应力集中系数超过2，峰值位置距相对应的工作面前方1.25m。由此可以判断工作面基本顶初次来压断裂步距为85m左右。

图8 不同层位上覆岩层支承压力峰值

2.4 根据工作面破坏场特征确定初次破断步距

随着推进距离增加，采场破坏范围逐渐增加，工作面上覆岩层和底板岩层的发育深度逐渐增加，且底板破坏发育深度略大于顶板发育高度。工作面煤壁前方煤体塑性破坏区宽度为2.5m，且随着推进距离的增加保持不变，破坏性质为剪切破坏。

图9为工作面推进80m和90m时采场围岩破坏场分布。由图9可知，当推进80m时，塑性区范围发展到工作面上覆8m细砂岩层，当推进90m时，工作面上覆10m砂岩在采空区中部全部垮落，垮落完成后，顶板细砂岩会在支架控顶区后部和切眼后部形成一定长度的悬顶，其垮落角大致为25～30°，工作面煤壁影响角为55～60°。从工作面围岩破坏范围判断工作面基本顶初次破断步距为80～90m。

图9 工作面推进采场围岩破坏场

2.5 现场实际测量结果

为了验证理论分析的准确性，在谢桥矿13216工作面进行了矿压观测。现场观测表明基本顶垮落时工作面机尾距开切眼为90m, 工作面机头距开切眼为82m, 平均86m, 加上切眼7.5m, 合计为93.5m。另参考与其相似条件的13118工作面(13118工作面的最大垮落步距为93m)，可以判断基本顶初次垮落步距L0=93.5m。

3 结论

(1)根据13216工作面具体的开采技术条件，建立了四边固支的薄板力学模型，推导出了顶板初次垮落步距公式，经计算顶板初次垮落步距为88.2m。

(2)针对谢桥矿13216工作面具体的地质与开采条件研究了其基本顶初次断裂步距，从煤层及上覆岩层的支承压力和塑性破坏的角度判断基本顶初次断裂步距，分别得到了初次破断步距的数值模拟结果，煤层应力判别值为80～90m，上覆岩层应力判别值为85m，围岩塑性判别值为80～90m，综合判别得到13216工作面顶板初次垮落步距为85～90m。

(3)由现场实际测量结果和数值分析结果对比分析可以看出，数值分析结果偏小，在误差范围以内且偏于安全，故而分析所得结果可靠，可以为其他相似工程提供参考。

[参考文献]

[1]何满潮，谢和平，彭苏萍，等.深部开采岩体力学研究[J].岩石力学与工程学报，2005，24(16)：2803-2813.

[2]牛锡倬.煤矿坚硬难冒顶板控制[J].岩石力学与工程学报，1988，7(2)：137-146.

[3]徐林生，谷铁耕.大同煤矿坚硬顶板控制问题[J].岩石力学与工程学报，1985，4(1)：64-68.

[4]宋永津.大同煤矿坚硬难冒顶板控制问题[J].岩石力学与工程学报，1988，7(4)：291-300.

[5]吴家龙.弹性力学[M].北京：高等教育出版社，2010.

[6]钱鸣高.老顶初次断裂步距[J].矿山压力与顶板管理，1987(1)：1-6.

[7]钱鸣高，刘听成.矿山压力及其控制[M].北京：煤炭工业出版社，1991.

[8]黄 炎.弹性薄板理论[M].北京：国防科技大学出版社，1992.

[9]丁大钧.薄板按弹性和塑性理论计算[M].南京：东南大学出版社，1991.

[10]蔡美峰，何满潮，刘东燕.岩石力学与工程[M].北京：科学出版社，2002.

[11]朱焕春，李 浩.论岩体构造应力[J].水利学报，2001(9)：81-85.