高斯烟雨扩散模型在空气中PM2.5实际问题的应用

董赫，翟哲，李夺，李伟凯

（1.黑龙江八一农垦大学信息技术学院，大庆 163319；2.黑龙江八一农垦大学工程学院）

随着国民经济飞速发展和城市化进程的日益加快，我国已有1/4的国土面积相继出现因大气细粒子污染增多而导致的雾霾天气，影响近6亿人的工作和生活。2012年2月29日，我国环境保护部公布了新修订的《环境空气质量标准》（GB3095—2012）[1]，增设颗粒物（粒径小于等于2.5 μm）浓度限值和臭氧8小时平均浓度限值。与《环境空气质量指数（AQI）技术规定（试行）》（HJ633—2012）的新标准同步实施。AQI分项监测指标为6个基本监测指标（二氧化硫SO2、二氧化氮NO2、可吸入颗粒物PM10、细颗粒物PM2.5、臭氧O3和一氧化碳CO）。新标准中，首次将产生雾霾的主要因素PM2.5浓度指标作为空气质量监测指标[2]。利用高斯烟雨扩散模型、多元线性回归等数学手段对空气中PM2.5的成因、扩散过程与气象因素之间的相关性进行深入分析，以西安市和武汉市气象局2013年1月至8月的空气污染物监测数据为依托，通过试验分析和仿真验证等方法，探索PM2.5与各污染物和风速之间的相关性；找到西安市高新西区空气中PM2.5浓度骤增并持续2 h时，空气中PM2.5浓度的分布与演变过程及相应的处理预案，为进一步研究空气中PM2.5的成因、监测和治理提供了一定的理论指导与科学依据。

1 空气中PM2.5与各污染物及气象因素的相关性分析

1.1 PM2.5与各污染物之间的相关性分析

选取武汉市某个监测站2013年1月至8月的AQI监测数据作为研究对象，首先从相关性和独立性方面入手，定量分析武汉市空气中6个基本监测值，得到各污染物之间的关联性。然后通过PM2.5与各监测指标的相关性推断这些污染物是否是PM2.5形成的主要气态物体，若与PM2.5的相关性显著，说明可能性较大，否则形成PM2.5污染源可能不止一个[3]。最后对PM2.5和几种强相关气态污染物做偏相关分析，验证分析结果的正确性。

采用积差法来计算各监测指标之间的相关系数。积差法就是用两个变量的协方差与两个变量的标准差的乘积之比，借助SPSS软件对PM2.5与各污染物之间进行相关性分析，得到结果如表1所示。

积差法数学模型：

表1 各监测指标相关系数Table 1 Correlation coefficient of the monitoring indicators

表1中N表示相关系数。由表1数据可知：（1）二氧化氮与二氧化硫相关性最强，与臭氧相关性最弱，与可吸入颗粒物线性相关最好，与一氧化碳线性相关最差。（2）可吸入颗粒物PM10与PM2.5相关性最强，与臭氧相关性最弱，与二氧化氮、PM2.5线性相关最好，与一氧化碳线性相关最差。（3）一氧化碳与PM2.5相关性最强，与臭氧相关性最弱，与臭氧线性相关最好，与二氧化氮线性相关最差。（4）臭氧与其他各项指标均为负相关，与一氧化碳线性相关最好，与其他指标线性相关均较差。（5）PM2.5与一氧化碳相关性最强，与臭氧相关性最弱，与二氧化氮线性相关最好，与二氧化硫存在一定的线性关联。

通过假设检验对样本来自的总体是否存在显著的线性相关进行统计推断，发现PM2.5、二氧化硫SO2、二氧化氮NO2和一氧化碳CO两两之间相关系数检验的概率P值都近似为零。因此，当显著性水平α=0.01时，认为他们两两之间存在较强的线性相关性。虽然臭氧和二氧化硫与可吸入颗粒物之间的相关系数检验概率分别为P=0.336和P=0.295，但是不能说明臭氧和二氧化硫与可吸入颗粒物之间存在线性相关性。

为了进一步探索PM2.5的成因，对上述结果进行偏相关分析。将臭氧作为控制一个偏相关变量控制，分析得到的各指标相互之间的相关性并没有明显影响，这说明臭氧对其他变量的相关性影响不大，这一结果也与前面所做的双变量相关性分析结果一致。下面采用逐步回归方法对PM2.5浓度与其他五项分指标之间的相关性系进行分析，借助SPSS软件分析结果如表2、图1所示：

表2 系数Table 2 Coefficient

通过对武汉市某监测站AQI监测数据中PM2.5与其他5种污染物指标的相关性分析，可以发现空气中PM2.5与二氧化硫SO2、二氧化氮NO2、一氧化碳CO及PM10的相关性显著，与臭氧的相关性不显著。因此得出的结论是：空气中PM2.5可能是由二氧化硫SO2、二氧化氮NO2、一氧化碳CO和PM10在一定条件下形成的。

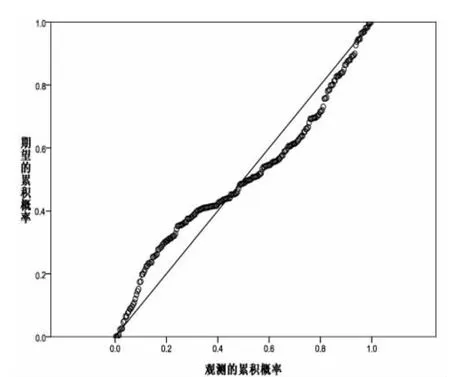
图1 回归标准化残差的标准P-P图（因变量：PM2.5）Fig.1 Standard PP Figure of regression standardized residuals（dependent variables：PM2.5）

表2中B表示相关系数，T表示回归参数的显著性检验值，Sig表示显著性，因变量为PM2.5。由表2和图1得到最终PM2.5浓度与各监测指标的多元回归模型为：

1.2 空气中PM2.5浓度与风速相关性分析

通过数据分析，2013年1月1日至31日武汉市空气中PM2.5浓度与风速之间的相关系数为-0.64，超过了0.01的相关信度检验。结合4月（春季）和7月（夏季）武汉市P空气中M2.5浓度与风速的相关性验证发现：PM2.5浓度和风速成负相关。（4月PM2.5浓度与风速的相关系数为-0.178，7月PM2.5浓度与风速的相关系数为-0.185，均超过0.01的相关信度检验。）由上述结果可以得出：PM2.5浓度与风速呈显著负相关，这主要是由于在高压反气旋的天气条件下，有利于污染物扩散，不易造成污染物的堆积。这一结论与实际情况相符[4-5]。

2 高斯烟雨模型在空气中PM2.5扩散过程中的应用

2.1 西安市13个监测子站空气中PM2.5浓度的时空分布

选取西安市区内13个监测站2013年1月至8月的AQI日平均监测数据为研究对象（表3），结合MATLAB软件编程绘出13个监测站所在地区空气中PM2.5浓度时空分布图，如图2所示。

表3 西安市13个监测站PM2.5日平均浓度与空气质量分指数Table 3 PM2.5 average concentration and air quality sub-indices of 13 monitoring stations in Xi′an

图2 西安市13个监测站PM2.5日平均浓度Fig.2 PM2.5 average concentration of 13 monitoring stations in Xi′an

对西安市13个监测站所在区进行污染评估。依据《环境空气质量指数（AQI）技术规定（试行）》标准中对污染物浓度的限值和空气质量指数的级别，对比西安市区内13个监测站所在区域的空气质量指数。空气质量良好的区域为：小寨、长安区、曲江文化集团、市人民体育场、兴庆小区监测子站所在区域，其余为受污染区域。

2.2 高斯烟雨扩散模型在PM2.5实际问题中的应用

假设2013年2月10日西安市高新西区监测子站PM2.5浓度在最高点处骤增一倍并持续2 h，利用高斯烟羽扩散模型预测西安市13个监测子站所在区重度污染和安全区域。通过查找气象数据，西安市2013年2月10日高新西区监测子站监测到的PM2.5浓度为500 μg·m-3为全年最高，当日西安市的天气情况为：霾、东北风～东风、微风、-1℃/5℃。针对上述问题，选取高斯烟雨扩散模型对其进行求解。高斯烟羽扩散模型是在大量实测资料分析的基础上，应用湍流统计理论得到的正态分布假设下的扩散模式，由于PM2.5属于大气中的悬浮污染物，因此可视污染源为高架点源[6-7]。

设u（x，y，z，h）是距离污染源位置的空间距离为h的点（x，y，z）处PM2.5的浓度[8]。任取一个闭曲面S，它所围的区域是G，由于扩散，从h到h+△h这段距离内，通过S流入G的质量为：

由高斯公式得：

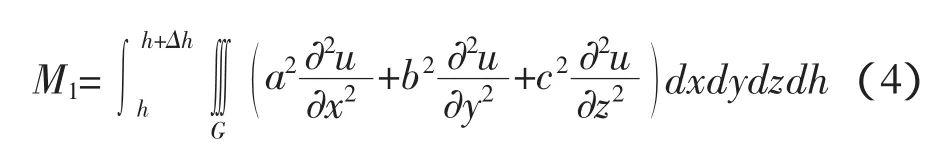
在扩散过程中由于土壤吸收、风及地表径流等造成PM2.5流失，使PM2.5的浓度有一定的衰减，G内的浓度减少为：

其中K2是衰减系数。

由物质不灭定律，PM2.5在G内由于扩散与衰减的合作用，积存于G内的浓度为Q=M1-M2，即：

PM2.5污染物的浓度计算公式为：

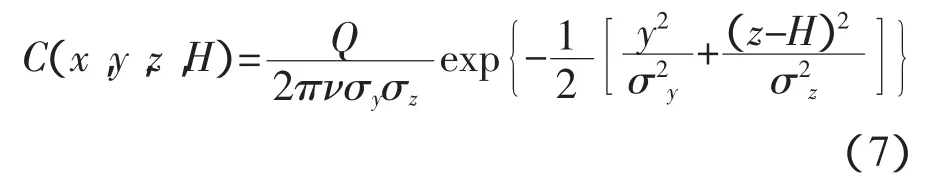
△h，H，G的具有任意性。

若要计算高架点源的地面浓度公式，可令Z=0，得：

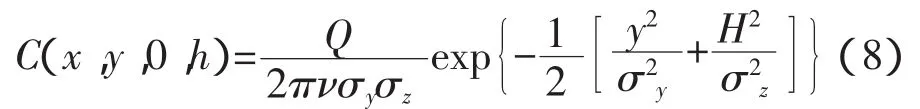
依据上式，若进一步令Y=0，则可得到沿X轴线上的浓度分布公式：

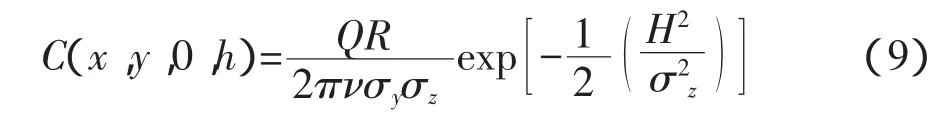
式中：

C—空间点（x，y，z）的污染物浓度，mg·m-3；

Q—源强，单位时间污染物排放量，mg·m-3；

v—平均风速，m·s-1；

σy，σz—污染物扩散系数，与大气稳定度和水平距离X有关，并随X的增大而增加。

其中，a2，b2，c2分别是沿x，y，z方向的扩散系数，扩散系数是表示扩散范围及速率大小的特征向量。为了较实际的确定这些扩散系数，采用帕斯奎尔（Pasquill）法（简称P-G法）。此方法是根据太阳辐射情况（云量、云状和日照）和距地面10 m高的风速将大气的扩散稀释能力划分为A～F六个稳定度等级[9]。

采用MATLAB软件编写高斯烟羽扩散模型（8）程序模块。程序中的源强、风速、大气稳定度参数和计算步长等可根据实际情况需要设置。经查找西安市各个地区面积图，得知高新西区检测子站所在的高新区土地面积为107 km3，城镇级别为属于城区，因此大气稳定度为D类。鉴于当日的天气情况（风速4.4 m·s-1），结合MATLAB软件辅助对上述假设情况计算分析，得到PM2.5浓度扩散图如图3所示。

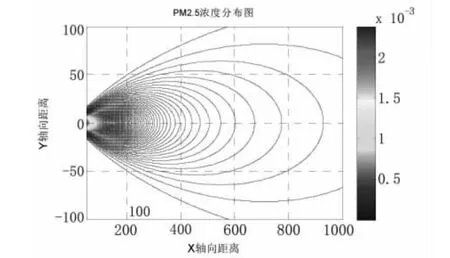
图3 PM2.5浓度扩散图Fig.3 Diffusion figure of PM2.5 concentration

图3清晰直观地反映了PM2.5污染源随时间向外衰减扩散的过程。中心点PM2.5浓度值为1 000 μg·m-3，模型近似为椭圆形，其X轴距离为900 m，纵轴距离为120 m，污染模型的面积为170 000 m2，结合当日风速（4.4 m·s-1）两小时后，椭圆形污染云向东北方向移动了30.4 km。此时西安市重度污染区域为高新西区、小寨区、曲江文化集团区、市人民体育场区、兴庆小区、经开区、草滩区、广运潭和纺织城。相对安全的区域为阎良区、临潼区、高压开关厂和长安区。

2.3 对高斯烟羽扩散模型的检验

对基于高斯烟羽扩散模型的空气中PM2.5浓度的发生和演变（扩散与衰减）模型进行拟合优度检验。结合SPSS软件的分析计算结果为R2=0.998，修正后的可决系数为0.992，这说明建立的模型对样本的拟合度良好。

3 高斯烟雨模型在实际问题应用中的分析和评价

3.1 高斯烟羽扩散模型

模型优点：基于高斯烟羽模式的高斯烟雨扩散模型的前提假设较符合实际情况，能充分反应了扩散的随机性，数学运算也较为简单。

模型缺点：建立扩散模型时忽略了其他气象因素间影响，在一定程度上增加了空气中PM2.5扩散过程的单一性和不确定性。

3.2 模型的改进

模型在保证指标尽量完整的基础上对评价系统进行了优化，使得问题的数学描述更为简单直观。但实际上还有部分监测指标与PM2.5的形成密切相关，而且是应该加以考虑的。在进行PM2.5浓度和各项监测指标间的相关性分析时，应尽可能的保持数据的完整性，只是分析了具有代表性的主要监测指标，应尽可能多的选取监测指标，提高各监测指标间相关性分析的完整度、精确度。

4 结论

通过建立高斯烟雨扩散模型，进一步探索产生雾霾的主要因素PM2.5的形成、扩散过程以及与风速之间的关系。以武汉市和西安市2013年AQI监测数据为基础，分析空气中PM2.5与其他污染物之间的相关性。预测了西安市高新西区监测子站PM2.5浓度骤增并持续数2 h时，污染严重和相对安全的区域。为研究空气中PM2.5成因、监测以及治理提供了一定的理论基础和科学依据。

［1］ GB 3095-2012.环境空气质量标准［S］.北京：中华人民共和国环境保护部，2012.

［2］ HJ 633-2012.环境空气质量指数（AQI）技术规定（试行）［S］.北京：中华人民共和国环境保护部，2012.

［3］ 李芳.西安市大气颗粒物PM2.5污染特征及其与降水关系研究［D］.西安：西安建筑科技大学，2012.

［4］ 杨洪斌，邹旭东，汪宏宇，等.大气环境中PM2.5的研究进展与展望［J］.气象与环境学，2012，28（3）：77-82.

［5］ 吴国平，胡伟，滕恩江，等.我国城市空气中PM2.5和PM10的污染水平［J］.中国环境科学，1999，19（2）：133-137.

［6］ 陈祖爵，陈潇君，何鸿.基于改进的混合高斯模型的运动目标检测［J］.中国图象图形学报，2007，12（9）：1586-1589.

［7］ 滕凯.无压流圆形断面收缩水深的简易算法［J］.黑龙江八一农垦大学学报，2013，25（1）：74-77.

［8］ 曲直.城市大气环境中PM2.5源解析成分谱的建立［D］.长春：吉林大学，2013.

［9］ 江鸿宾，邓顺熙，郭庆妮，等.基于一种改进的高斯型研究危险气体短时泄漏后扩散规律［J］.甘肃科技，2013，29（12）：42-45.