基于多层神经网络的超宽带室内精确定位算法

沈冬冬，李晓伟，宋旭文，贺志楠

(西安电子科技大学 电子工程学院，中国 西安 710071)

无线通信技术［1］的发展使得对于无线定位的需求日趋增加，传统的室外定位技术已被广泛应用，人们对复杂室内环境精确定位的需求越来越强烈，比如消防、医疗等。超宽带(Ultra－WideBand，UWB)［2］因为是一种无载波通信技术，以及GHz 量级的带宽，所以可有效地降低发射信号功率、系统复杂度的同时提供厘米级的定位精度。

根据目前的研究状况，超宽带室内精确定位算法可以分为5 类:基于信号到达时间(Direction of Arrival，TOA)的定位算法［3］、基于信号到达时间差(Time Difference of Arrival，TDOA)的定位算法［4］、基于信号到达角度(Angle of Attack，AOA)的定位算法［5］、基于接收信号强度(Received Signal Strength Indication，RSSI)的定位算法以及混合定位算法［6］。考虑到实现的可能性以及复杂程度，基于信号到达时间(Time of Arrival，TOA)的定位算法被排除，同时考虑到定位的精度，基于接收信号强度(RSSI)的定位算法也被排除。

随着对定位精度要求的不断提高，单一定位方法无法满足需求，融合两种及以上的混合定位方法就成了一个发展趋势。文献［7］讨论了TDOA/AOA 混合定位方法，获得了比TDOA、AOA 单一定位算法更高的定位精度。因此，本文提出了一种基于多层神经网络的超宽带混合定位算法，利用多层神经网络对到达时间差(TDOA)和到达角度(AOA)测量值中的非视距传播误差进行修正，来提高超宽带的定位精度，与传统TDOA/AOA 定位算法相比，定位精度有所提高。

1 仿真信道模型

工作组提出了3 不同的模型，本文研究的方向为室内环境下的超宽带精确定位，基于这个目的选择2 ～10 GHz 的超宽带信道模型作为仿真的信道模型，着重研究住宅环境。2 ～10 GHz 的超宽带信道模型是建立在路径增益模型(Pathgain)、功率延时分布模型(Power Delay Profile)和小尺度衰落模型(Small－scale Fading)的基础上。

1.1 路径增益模型

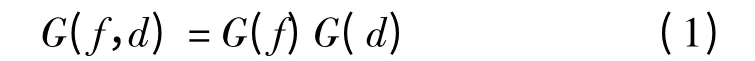
路径增益［8－9］与频率的关系函数为k 是频率对于路径增益的影响因子。

路径增益与距离的关系函数为G(d)=G0－是基准距离，设定为1 m，G0是距离d0=1 m 处的路径增益，n 的值取决于实际环境是视距(Line－of－Sight，LOS)还是非视距(Nonline－of－Sight，NLOS)。可得到路径增益、频率及距离之间的函数为

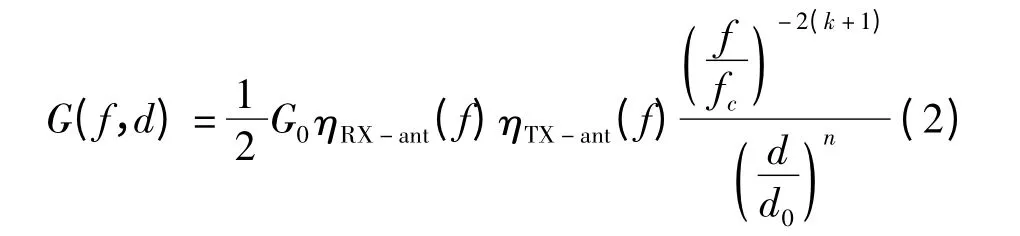
式中，ηRX－ant(f)是接收天线的增益;ηTX－ant(f)是发射天线的增益。

如果考虑阴影(Shadow)的影响G(d)=G0－为服从均值为0;方差为σ 的高斯分布的随机变量，不同环境表示为不同的具体数值。

1.2 功率延时分布

本文主要研究室内环境下的超宽带精确定位，因此只考虑信号到达率(Ray Arrival Rates)。信号到达率由综合两个泊松过程得到

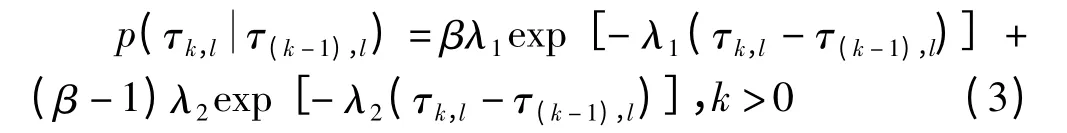
τ0，l=0，β 为混合概率，λ1，λ2为到达率。

IEEE802.15 工作组借鉴了S－V 模型来拟合信号的分簇到达时间(Cluster Arrival Times)，可用冲击响应hdiscr(t)来描述

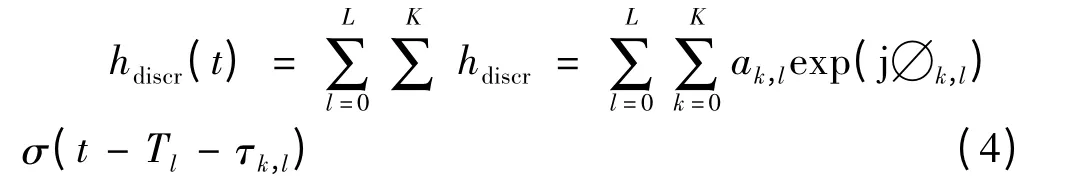
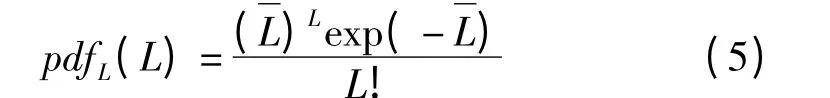
1.3 小尺度衰落(Small－scale Fading)

IEEE802.15.4a 的小尺度衰落采用Nakajami 信道模型

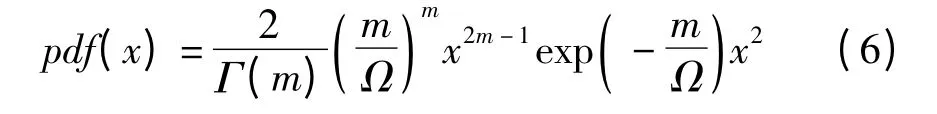
2 超宽带TDOA/AOA 混合算法的改进

2.1 TDOA/AOA 定位原理

TDOA 的几何原理是双曲线测量定位，AOA 的几何原理是三角测量定位，二维空间原理如图1 和图2所示。

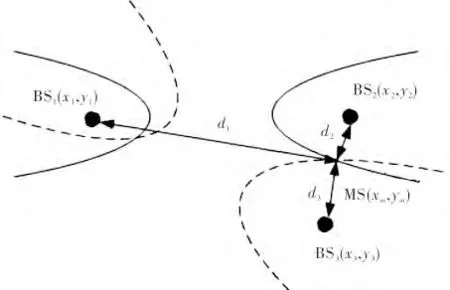
图1 二维空间TDOA 原理图

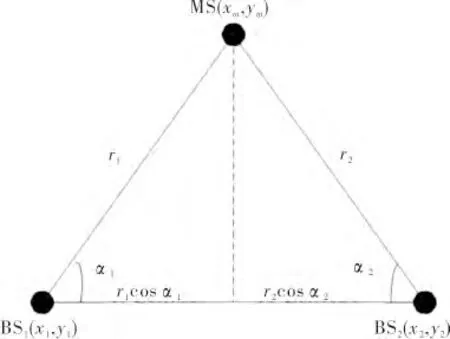
图2 二维空间AOA 原理图

如图1 所示(x1，y1)、(x2，y2)、(x3，y3)为3 个已知节点位置，则待测节点(xm，ym)与已知节点的位置关系如下

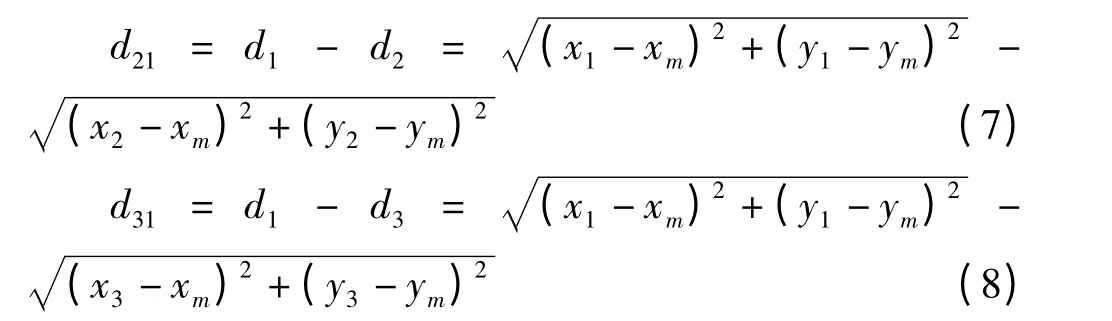
如图2 所示(x1，y1)和(x2，y2)为两个已知节点位置，角度值α1、α2为通过定向天线测得的相对角度值。则待测节点(xm，ym)与已知节点的位置关系如下

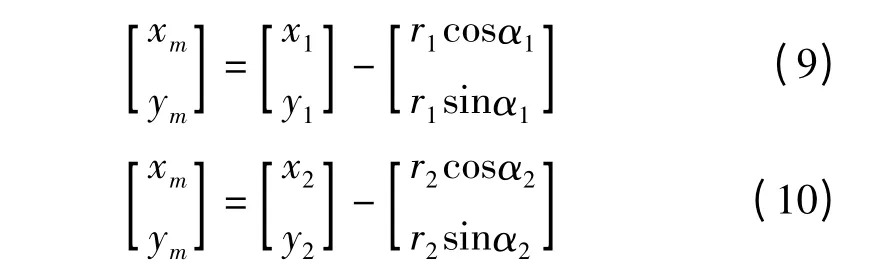
2.2 改进的TDOA/AOA 混合算法

研究需要获取三维位置信息，根据上述TDOA/AOA 定位原理，定位基站至少需要4 个，基站数量增加可以提高定位精度，但相应的成本也随之增加，目前市场上每个基站的售价约5 000 元，以下是在4 个基站的情况下建立的多层神经网络模型［10－12］。

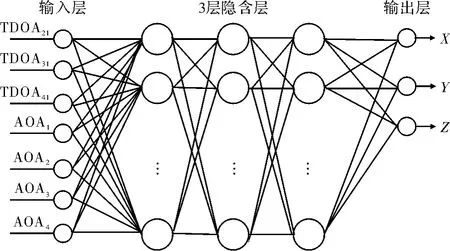
图3 多层神经网络模型图

(1)输入层由参与定位的4 个基站提供的3 个TDOA 测量值和4 个AOA 测量值所组成，因此，输入向量可表示为

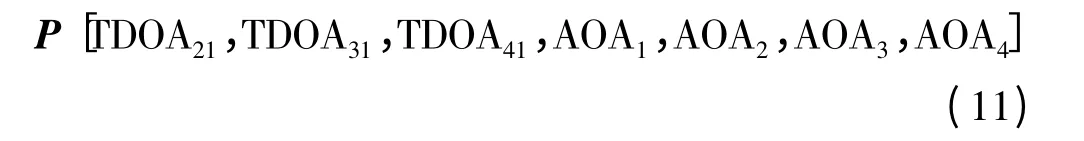
(2)隐含层的层数、隐含层各层神经元数目以及各层激励函数的选择，目前还没有理论上的指导。隐含层的层数、神经元数目增加可以提高定位精度，但计算的复杂性也随之增加。根据仿真数据如图4 所示，隐含层的层数选为3 层。根据基站布设模型，隐含层各层神经元数目选为9。

图4 隐含层层数仿真图

各层激励函数

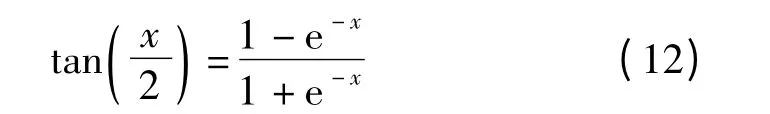
(3)输出层由3 个神经元构成，输出向量O［X，Y，Z］。基于神经网络的定位算法具体步骤:1)利用Matlab神经网络工具包，建立本文提出的神经网络模型。2)训练神经网络模型，如图5 所示。

第一层，定位范围1.8 m×1.8 m，每200 组数据训练一个神经元，一共训练9 个，各神经元间距＜0.5 m。

第二层，定位范围0.9 m×0.9 m，每150 组数据修正一个神经元，将第一层的9 个神经元全部修正一次，各神经元间距＜0.4 m。

第三层，定位范围0.4 m×0.4 m，每100 组数据修正一个神经元，将第二层的9 个神经元全部修正一次，各神经元间距＜0.3 m。

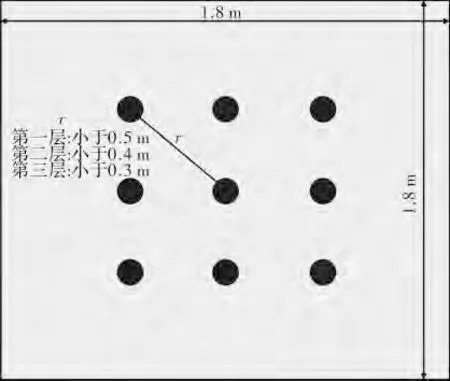
图5 多层神经网络中的神经元间距调整图

3 仿真与分析

为检验该算法的实际性能，用Matlab 软件对本文定位算法进行仿真，对本文算法和单纯采用AOA、TDOA、TDOA/AOA 算法进行了比较，仿真结果如图6所示。

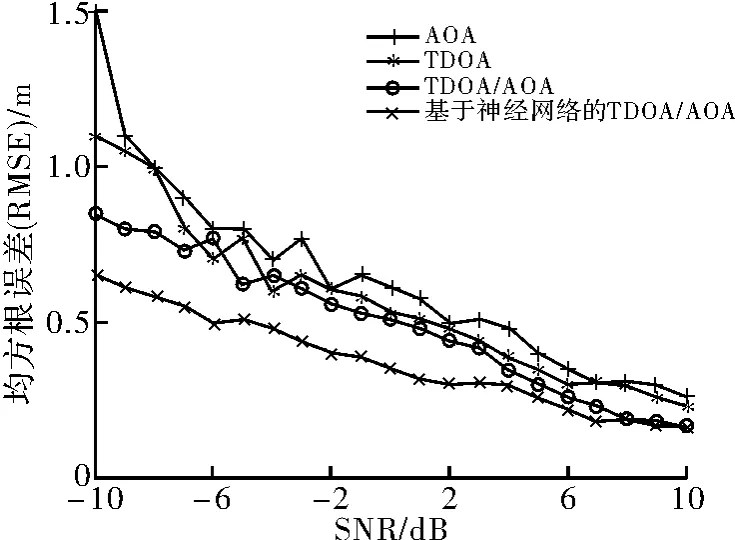
图6 多种算法误差对比

如图6 所示，在相同信噪比环境下，利用多层神经网络的TDOA/AOA 算法能够明显降低均方根误差。如果当信噪比降低时，采用多层神经网络的TDOA/AOA 算法比原TDOA/AOA 算法效果更明显。

4 结束语

本文研究了超宽带无线定位的原理和算法，在不增加设备复杂性的前提下，在TOA/TDOA 定位算法的基础上，利用多层神经网络对到达时间差和到达角度测量值中的非视距传播误差进行修正，提出了多层神经网络TOA/TDOA 定位算法，算法能够明显的降低均方根误差。

［1］ 张士兵，张力军.超宽带无线通信及其关键技术［J］.电讯技术，2004(5):1－6.

［2］ 徐玉.超宽带无线技术标准之争［J］.电信科学，2004(3):33－35.

［3］ XU Yubin，JIANG Weilin，SHA Xuejun.TOA estimate algorithm based uwb location［C］.IEEE International Forum on Information Technology and Applications，2009，1:249－252.

［4］ CHEN C K，GARDNER W A.Signal－selective time－difference of arrival estimation for passive location of man－made signal sources in highly corruptive environments［J］.IEEE Transactions on Signal Processing，1992，40(5):1185－1197.

［5］ JUAN C，MIGUEL E.Angela hernandez－solana，antonio valdovinos，comoarison of algorithms for uwb indoor location and tracking systems［C］.IEEE Vehicular Technology Conference，2011:1－5.

［6］ VENKATRAMAN S，CAFFERY J R J.Hybrid TOA/AOA techniques for mobile location in non－line－of－sight environments［C］.IEEE Wireless Communication and Networking Conference，2004，1:274－278.

［7］ YANG Chunhua，HUANG Yi，ZHU Xu.Hybrid TDOA/AOA method for indoor positioning systems［C］.IEEE Location Technologies，2007:1－5.

［8］ 张在琛，毕光国.超宽带室内信道模型［J］.电气电子教学学报，2004，26(6):60－63.

［9］ VENKATESH S，IBRAHIM J，BUEHRER R M.A new 2－cluster model for indoor UWB channel measurements［C］.IEEE Antennas and Propagation Society International Symposium，2004，1:946－949.

［10］ZHAO Y.Standardization of mobile phone positioning for 3G systems［J］.IEEE Communication Magazine，2002，40(7):108－116.

［11］ ZAMIRIJAFARIAN H，MIRSALEHI M M，AHADI －AKHLAGHI I，et al.A neural network－based mobile positioning with hierarchical structure［C］.IEEE Vehicular Technology Conference，2003.

［12］MARANO S，GIFFORD W M，WYMEERSCH H，et al.NLOS identification and mitigation for locatization based on UWB experimental data［J］.IEEE Journal on Selected Area in Communications，2010，28(7):1026－1035.