单二次雷达无线电干扰源定位算法及误差分析

王广宇

(民航东北空管局 技术保障中心，辽宁 沈阳 110169)

单二次雷达是民航空中交通管理的重要技术设备，但无线电干扰会造成单二次雷达作用距离减小、降级维护、雷达主备通道间频繁转换及二次代码混乱等现象，造成飞行器定位模糊，严重干扰雷达管制程序的实施。因此需对无线电干扰源在二维和三维空间内，进行定位计算及校验。常规的理论方法为双曲线定位:即在二维平面内，无线电干扰源信号到达两个雷达站的时间差确定一对以两站为焦点的双曲线，并利用3 或4 个站形成两条双曲线，可得到两队双曲线的两个交点。再利用其他辅助信息去除定位模糊，以此可确定干扰源的位置。而三维空间中，至少需形成3 对双曲线产生的交点［1－2］。本文在此基础上，结合电磁波的空间传播特性，实现精确的误差分析和定位判别，确定雷达站、无线电干扰源与障碍物3 者之间的相对位置关系，形成工程应用中的实用算法，以达到对干扰源定位的目的。

1 二维平面的定位算法

如图1 所示，A、B、C 分别设为无线电干扰源、单二次雷达1 和单二次雷达2。若此3 点不在同一直线上，符合应用交叉定位原理的必要条件。则可在产生无线电干扰后，打开两部雷达的原始视频，获得干扰源的定位方向线AB 和AC，A 即两雷达原始视频的交汇点，也是对无线电干扰源所初步确定的位置［3］。两条定位方向线的长度分别设为γ 和β，但其长度不可定。

图1 二维定位算法示意图

依靠二次雷达的平面位置显示器的地理坐标及测距功能，可知两部雷达距离为α。以C 为例，借助正北方位角显示功能，得到无线电干扰源方向线AC 的正北方位角θ2，与另一部雷达的方向线BC 的正北方位角θ1。同理，以B 为中心点，获得无线电干扰源方向线AB 的正北方位角γ1，与雷达C 的方向线BC 的正北方位角γ2。则三角形ABC 中，可得出B、C 两角的值为

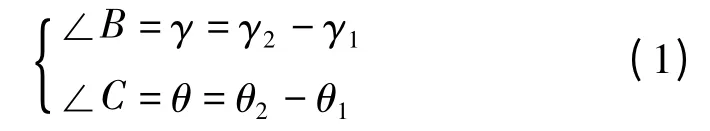
式中，、为无线电干扰源与两部单二次雷达B、C 连线所得方位角。由此可知三角形ABC 中两角值及所夹边BC 值，可依据三角形正弦定理

得出如下结果

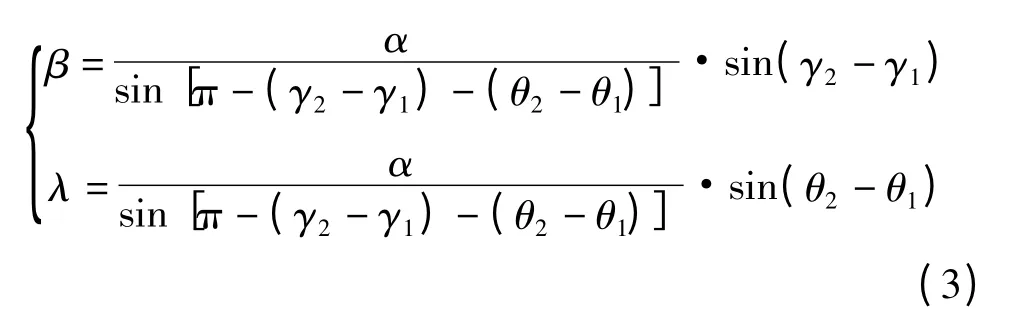
2 基于三维空间的定位算法

以上算法只能得出在XOY 平面的无线电干扰源的坐标点，无法算出无线电干扰源的高度。实际应用中，无线电干扰源对高大建筑物或山体具有反射或折射特性，易造成两部雷达原始干扰视频交汇点偏移，进而产生测距误差［4］。因此需定位计算出无线电干扰源的三维空间坐标，因目标干扰源的俯仰角不可测，所以应尽最大可能避免引入俯仰角为中间变量或参数。

如图2 所示，无线电干扰源空间坐标为(xT，yT，zT)，雷达站1 和2 的空间坐标分别为(x0，y0，z0)，(x1，y1，z1)，干扰源回波到达两部雷达时间分别为t0、t1，相应空间距离为r0、r1。此算法中引入时差参数Δt1=t1－t0，作为目标干扰源回波到达两部雷达的时间差［5］。该参数获取方式为:将两部单二次雷达的测试应答机与各自的本地时钟信号拟合后，得出到达时间差估计，再通过各自数据链送入雷达自动化处理系统中，进行时钟误差校正，最终算出到达时间差;也可通过原子时钟同步方式，即由原子时钟获得本地高精度时间信号，再通过数据网络动态校准远端两部雷达同步时钟，从而得到干扰源回波到达的时间差。

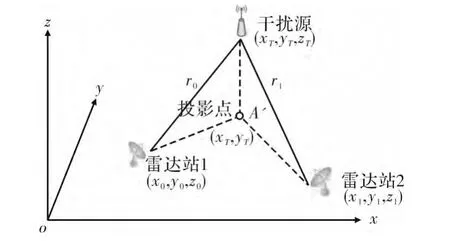
图2 三维定位算法示意图

依据以上参数，可列出方程组

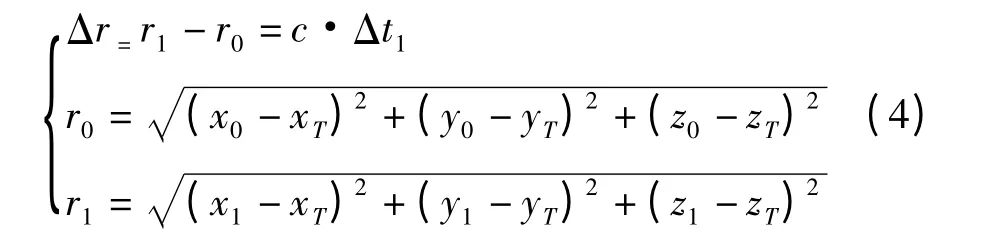
式中

对于矩阵A，由于其行数小于列数，且显然存在rank(A)=1，则可知式(5)在X 的欧氏范数空间内必有最小范数 解［6］，其 最小范数解为

式中

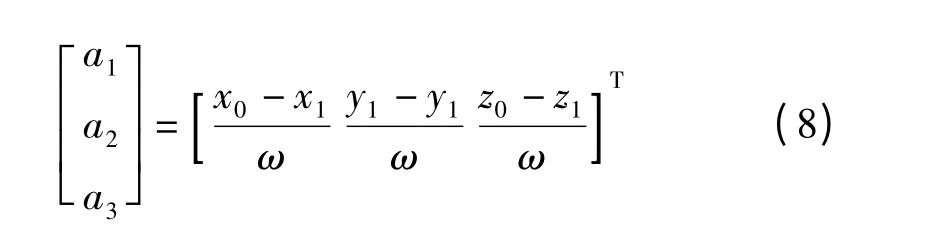
其中

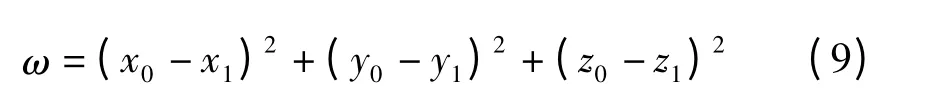
设bi=aiD1，ci=ai·Δr1，i=1，2，3。上式可转化为以r0为参数的方程组

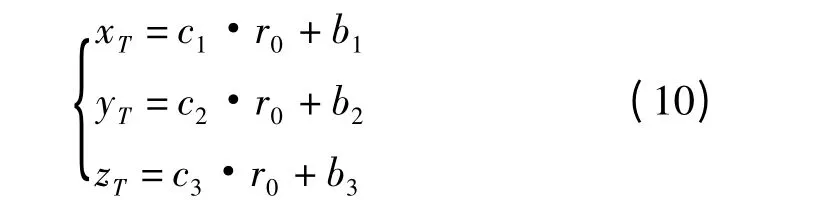
将式(10)与式(4)联立，可得

在上式的基础上，以r0为未知数，建立起一元二次方程

由式(4)可知，r0必有解，不存在b2－4ac ＜0，则r0可求，即

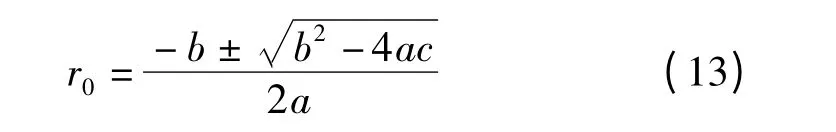
上式中各参数为

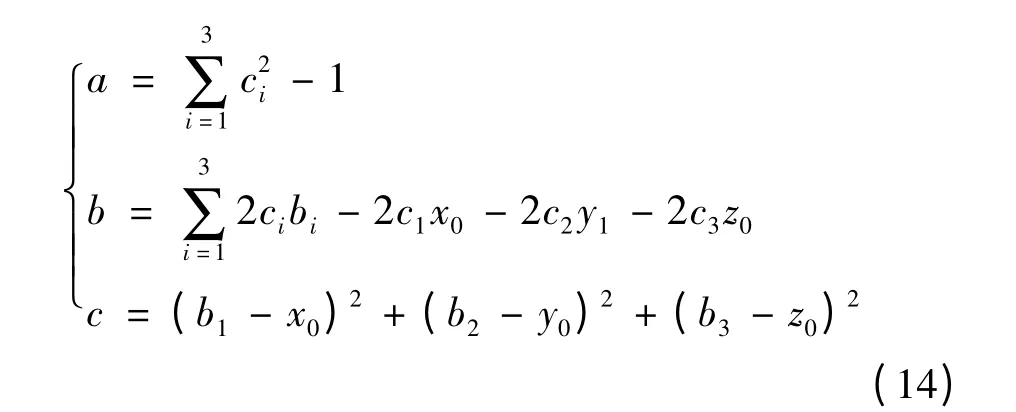
将式(13)计算结果代入式(10)中，即可得出无线电干扰源的空间坐标。式(13)中r0有两个解r01和r02，若r01·r02＜0，则取正值为解;若r01、r02均为正值，则需借助其他辅助信息进行最后定位以消除误差。

3 基于原始视频的定位判别

如图2 所示，无线电干扰源在XOY 平面的投影点A'的坐标为xT，yT。因图1 与图2 所用坐标体系不同，所以不能直接校验xT和yT，尚需借助其他参数。已知图1 中B 点和C 点分别对应图2 中的雷达站1、2。将三维空间转换为二维平面，则图1 中λ 和β 的表达式为

当r01、r02均为正值时，将r01、r02分别代入式(10)中，r01对应所得值设为xT1和yT1，r02对应所得值设为xT2，yT2。将(xT1，yT1)及(xT2，yT2)代入式(15)中，对应可得(λ1，β1)，(λ2，β2)。最终，将以上二值与式(3)计算后所得λ，β 比较。从(xT1，yT1)和(xT2，yT2)中，选取与式(3)计算结果相等或较接近的正值作为r0的解，该算法实质是校验无线电干扰源在XOY 平面的投影点A'是否与图1 中的A 点重合。基于此算法，可在r01和r02中，选取一个值作为真实解。至此，完成初始定位判别。

若(xT1，yT1)和(xT2，yT2)所对应的值均与式(3)计算结果相差较大，则需引入方位角γ 和θ，作为比照参数，判定误差产生方向，并重新进行比较及误差分析。

4 二次定位判别及误差分析

λ，β 产生较大误差的原因在于:任何一部单二次雷达不能通过原始视频获得无线电干扰源的俯仰角，且两部雷达原始视频的交叉点既有可能是干扰源在XOY 平面投影的真实位置;也有可能是某一障碍物。即如图3 所示，该障碍物为无线电干扰源的电磁波折射点或反射点，测距误差由此产生。

依靠二次雷达原始视频，可保证二次雷达、干扰源及障碍物此3 点位于同一平面，且该平面垂直于XOY平面［7－8］，因此可推断:干扰源必在雷达站1 的γ 方位角上，或位于雷达站2 的θ 方位角上。由此可在上述两个方向上，建立起两个垂直于XOY 平面的辅助定位面。

在经过雷达站1 的γ 方位角上辅助定位面内，若干扰源1 处于雷达站1 和障碍物之间，会因电磁波的反射导致所测得λ 值偏大;反之，干扰源2 处于雷达站1和障碍物连线的延长线上，则因电磁波的折射使得所测λ 值偏小。同理可知，在经过雷达站2 的θ 方位角辅助定位面上，也会因干扰源相对于障碍物位置的变化，引起所测得β 值得到相同变化。

综上所述，在俯仰角未知的情况下，并假定障碍物可能存在时，必须借助方位角γ、θ 确定电磁波折射或反射的产生方向。而γ'、θ'可由图3 所确立的几何关系推出

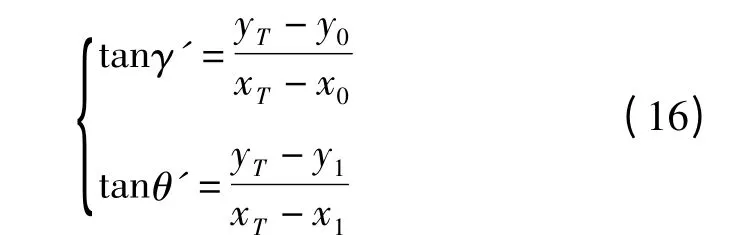
此处所指方位角γ、θ、γ'和θ'，是在立体几何空间内所得出的，由单部二次雷达、干扰源及障碍物此3 点所确定的平行于Z 轴的平面与X 轴的夹角。

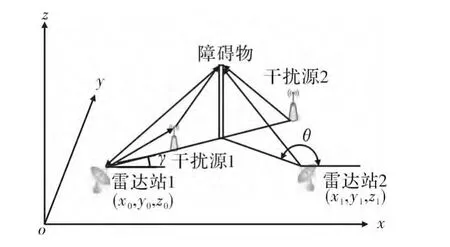
图3 障碍物与干扰源位置关系

将r01及r02在式(10)中所得值(xT1，yT1)、(xT2，yT2)代入式(16)中，对应可得(γ'1，θ'1)，(γ'2，θ'2)。现以r01为例，对障碍物所处位置及r01对应的空间坐标，做出如下判断:

(1)γ'1=γ，且θ'1=θ，则障碍物不存在，无电磁波折射和反射，r01显然为真实值，舍去r02。

(2)γ'1=γ，且，则障碍物存在于雷达站1的方位角γ 方向上，在此方向上产生电磁波的折射或反射。舍去r02与θ 值，将依据式(15)所得值λ1与式(3)中λ 比较，若λ1＞λ，则可知障碍物位于雷达站与无线电干扰源之间;反之，可判定干扰源位于雷达站与障碍物之间。

(3)γ'1≠γ，且θ'1=θ，则可知障碍物存在于雷达站2 的方位角θ 方向上，即在此方向上产生电磁波的折射或反射。舍去r01与γ 值，将依照式(15)所得值β2与式(3)中β 进行比较，若β2＞β，则可知障碍物位于雷达站与无线电干扰源之间;反之，可判定干扰源位于雷达站与障碍物之间。

现今某些二次雷达使用S 模式接收机处理器，可兼容常规模式雷达。因此，S 模式单二次雷达将会形成两个方向的原始干扰视频［9］，与另一部常规二次雷达形成两个空间交汇点，即障碍物反射或折射点(xzf，yzf，zzf)，干扰源坐标点(x，yIS，zIS)，且上述两个坐标点通常与常规二次雷达坐标点不在同一平面内。依据电磁波反射及折射必要条件，可知zzf＞zIS［10］。对于这两个空间交汇点，通过本文所述方法，可对应获得时差参数Δt1和Δt2，并分别独立使用三维空间定位算法和本文所述判别法则，获得各自的唯一坐标值(xT1，yT1，zT1)，(xT2，yT2，zT2)。若存在zT1＞zT2，可判定(xT2，yT2，zT2)必为无线电干扰源的空间坐标。

5 结束语

基于两部单二次雷达的空间坐标及无线电干扰源回波到达两部雷达的时差参数，列出矩阵方程，求解该方程的最小范数解，以此得到目标干扰源的空间坐标是完全可行的。而后借助两部雷达的原始视频，在二维空间内进行初始定位判别，并在引入新的方位角概念和建立起两个辅助空间定位面后，再进行二次定位判别和误差分析及估计，可从理论上消除由电磁波折射或反射造成的定位模糊。而S 模式接收机两个方向的原始视频，可有助于更快地进行障碍物及干扰源的定位。但应考虑到，若无线电干扰源本身或干扰源在水平面的投影点，位于两部雷达连线上或其延长线上，则两部雷达原始干扰视频交汇成一条直线，将导致无法进行初始定位判别，也不可能建立起两个方位角及辅助空间垂直定位面上进行的二次定位判别。因此，重新选择两部二次雷达以实现交叉定位，将必不可少。

［1］ 廖海军.多站无源定位精度分析及相关技术研究［D］.成都:电子科技大学，2008.

［2］ 刘琪，孙仲康.双基地两坐标雷达对三维目标的最优化定位［J］.电子科学学刊，2000，22(3):366－369.

［3］ 中国民用航空总局.MH/T4010－2006 空中交通管制二次监视雷达设备技术规范［S］.北京:中国标准出版社，2006.

［4］ 卢宇，吴宏刚，徐自励.基于TDOA 残差分析的多点定位抗干扰方法［J］.计算机应用，2013，33(5):1470－1472.

［5］ 马晓岩.现代雷达信号处理［M］.北京:国防工业出版社，2013.

［6］ 谢绪恺.现代控制理论［M］.沈阳:辽宁科技出版社，1980.

［7］ 唐皓，吴季达，鲁东生.基于TDOA 原理计算信号源位置的算法探讨［J］.计算机科学，2011，38(10A):467－469.

［8］ 戈稳.雷达接收机技术［M］.北京:电子工业出版社，2006.

［9］ 杨书玲.三维时差频差定位算法研究［J］.无线电工程，2013，43(7):15－16.

［10］杨林，周一宇，孙仲康.TDOA 被动定位方法及精度分析［J］.国防科技大学学报，1998，20(2):50－53.