求解异常高压气藏单相非线性渗流模型的一种新方法
郑 琴 董传杰 高淑芳
(中国石油大港油田勘探开发研究院)
求解异常高压气藏单相非线性渗流模型的一种新方法
郑 琴 董传杰 高淑芳
(中国石油大港油田勘探开发研究院)
针对传统异常高压定参数渗流模型不能满足工程需要的现状,建立渗透率、孔隙度等参数随有效应力变化的异常高压气藏单相非线性渗流模型。为使井底附近压力分布的计算更加准确,采用对数等距网格进行网格剖分,即越靠近井底处,网格分布越密,沿径向向外,网格逐渐变稀。在求解差分方程时,创新采用自适应延拓法,克服了传统Newton法、Brown法等数值方法要求迭代初值与真解充分接近的局限性。编程计算结果表明:考虑了渗透率、孔隙度等参数随有效应力变化规律的异常高压气藏单相非线性渗流模型比常用的常系数模型更加贴近工程实际,自适应延拓法的应用对解决初值问题及奇异问题也是简单有效的。
异常高压 非线性 渗流 有限元 数值模拟
国内现已发现多个异常高压气田。气藏衰竭式开采过程中,流体压力逐渐下降,储层岩石骨架受到的有效应力会随之增大,导致岩石发生显著的弹塑性形变,并减小岩石孔隙度、渗透率、压缩系数等物性参数的值,进而影响到气藏的最终开发效果。因此,在进行异常高压气藏研究时应充分考虑储层应力敏感性的影响,掌握储层物性参数随有效应力改变的变化规律,建立能更准确描述异常高压气藏渗流机理的非线性渗流模型,进而更加精确地对该类气藏进行开发动态模拟和最优控制。
1 储层物性参数的应力敏感性
国内外专家从上世纪70年代起,就开始研究孔隙度随净围压变化的规律,他们得出了孔隙度随有效压力呈指数式变化的结论[1-4]。这种指数式关系可用数学表达式写为:

类似,渗透率与有效压力之间的关系也可用指数函数式来表达:

2 异常高压单相非线性渗流微分方程的建立
气体的等温压缩系数:

由(1)、(2)知地层渗透率、孔隙度随有效应力呈指数式变化。由状态方程、运动方程和连续性方程最终可得:

在式(4)中,由于K、Z都是压力的函数,因此不能提到算子之外,引入拟压力函数的概念[5]:

经变换可得到以拟压力形式表示的异常高压气藏不稳定渗流微分方程:

因αΦ的值与气体压缩系数C(p)比较起来非常的小,可以忽略不计。令c=C(p)+αΦ≈C(p),则得到与常见形式相同的异常高压气藏不稳定渗流微分方程:

在圆柱坐标系(r、θ、z)中,由于地层均质,压力p与θ角度无关,可得到柱坐标形式下的渗流微分方程:

3 异常高压裂缝性气藏变系数渗流模型数值方法研究
前面我们已经推导出了异常高压气藏单相非线性渗流方程,结合相应的初边值条件,如果仅考虑二维平面圆形封闭边界问题,模型可简化为:

3.1 网格的选择
根据渗流力学理论可知在井底附近存在压降漏斗,井筒附近地层压力变化非常大,远离井筒区域压力变化小。因此,采用非等距网格进行定义域剖分,即沿径向向外,网格由密逐渐变稀,以达到所需的计算精度。为使计算结果具有更佳的稳定性,我们在这里采用对数等距点中心网格进行划分。
3.2 差分方程的形成
根据前文分析,孔隙度、渗透率随有效压力呈指数式变化规律,而气体在开发过程中随压力减小而发生膨胀,其压缩系数变化趋势与岩石压缩系数相反,是随有效压力增大而增大的,假设其变化也遵循指数式变化的规律:


引入差分记号,再代入传导系数的边界,最终可得:

简记Pn+1为Pi,引入记号后有:

式中:

3.3 定解条件的处理
·初始条件:

作为初始层上的沿空间各节点处的函数值,即
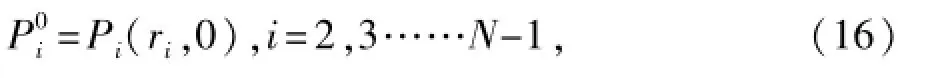
·内边界条件:


·外边界条件:

可得:

3.4 非线性方程组
综合式(13)、(18)、(20)即可得到由N个方程构成的N元非线性方程组:

于是,对(14)式模型的求解,就转化成了对非线性方程组(21)的逐层求解。
3.5 自适应延拓法
下面我们讨论对(21)式表示的方程组进行求解的算法。设F:D⊂Rn→Rn,含有n个自变量的N元非线性方程组问题F(x)=0的求解可选取常用的Newton法、Brown法、割线法、拟牛顿法等。而这些方法都具有局部收敛性,在使用它们进行计算时要求迭代初值x0与解x*充分接近,因此实际使用时往往很难满足。延拓法是一种可以扩大局部收敛区域的算法,它在计算非线性方程组的迭代初值时是一种很有效的方法。在运用延拓法寻求得到充分靠近真解的初值后,还可以和其他局部收敛的迭代算法复合起来使用,以求得更加精确的近似数值解。
在使用延拓法求F(x)=0的解x*∈D时,先要人为地引入一个参数t,构造函数族H(x,t),使之满足同伦条件:

其中F0(x)=0的解已知。
构造H(x,t)的方法有很多种,但并非任意构造H(x,t)的都有效。在此,根据方程的具体形式,我们取

引进一个控制参数对普通延拓法进行改进,使其除了保持一般延拓法的大范围收敛性外,还可通过改变参数,重新定义同伦,以避免Hx(x(t),a(t),t)出现奇异。在进行具体的计算机数值求解时,可自动控制非奇异参数解决奇异问题,并能自动选择步长以及判断是否进入Newton迭代收敛域,这种改进的延拓法就是自适应延拓法。
将(23)式中的常量a参数化为a(t),从而构造新的同伦:

这里,a(t)是一个含参的已知函数,在tε[0,1]上连续可微,比如a(t)=a(1+t)。
显然,对于(24),当时t=0,时H(x0,0,a(0))=F(x0),当t=1时,H(x,1,a(1))=F(x),故H(x(t),a(t),t)满足同伦条件(22)。
为了求解x(1),在(23)的两端对t求导并整理得:

其中g(t)=a(t)(1-t)。在t∊[0,1]上,由于a(t)的连续可微性,g(t)在上t∊[0,1]也是连续可微的。
于是,与(24)等价的Cauchy问题是

容易得出,只要g(t)取得足够大,总能使矩[F′(x)+g(t)I]阵非奇异。而改变a(t),就可以重新定义H(x(t),a(t),t)。

首先采用Euler法进行迭代初值的近似:

进一步精确化则采用Newton迭代:

在计算F′(x)时采用差商近似J(x,δ),精确化则采用Newton迭代法,在Euler公式中结合使用1次2阶的中点求积公式,于是编程进行数值计算的迭代算法可以写成:

式中

ej=(0,…1,…,0)T为第j个分量为1的单位坐标向量,i,j=1,2,……n。
4 异常高压气藏单相非线性渗流模型算例
本文用理论数据模拟了某异常高压气藏。设原始地层压力pi=70 MPa,原始孔隙度10%,初始渗透率0.03μm2,原始气体压缩系数,4×10-3MPa-1,αΦ=0.0008,αK=0.06,αc=0.015,黏度为0.35 mPa·s,气层有效厚度20 m,产量q=5×104m3,,井筒半径rw=0.1 m,地层半径re=1000 m,根据换算得初始拟压力Pi=1120。构造非等距网格如图1所示:
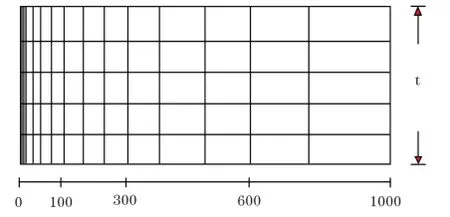
图1 有限差分非等距网格图
得到有限差分方程组后,直接采用Newton法进行迭代求解,取初值,3……N-1,无法得到收敛值。采用自适应延拓法,求得当生产进行300天后,拟压力及压力沿径向距离的分布。

图2 300天后拟压力随径向距离变化趋势图

图3 300天后压力随径向距离变化趋势图
由图中可以看出,在同一时间内,距离气井远近不同的点,其压力变化是不一样的,离井越近,压力下降越快,离井越远,变化相对越平缓。

图4 拟压力随时间变化趋势图

图5 压力随时间变化趋势图
图4、图5是根据程序求得的井底附近拟压力及对应的压力随时间变化的趋势图,由图中可以看出,拟压力和压力变化的趋势是一致的。与低压和常压气藏不同,在异常高压气藏开发初期,压力下降较中后期缓慢,这可以解释为由于储层岩石具有较高的压缩性,随地层压力的下降,岩石颗粒膨胀使压力得以保持。到了气藏开发后期,岩石压缩系数降低,气体压缩系数增大,此时岩石压缩系数相对于气体压缩系数已很小,气产量主要由天然气膨胀贡献,所以气藏的动态非常接近于定容气藏。异常高压气藏的这个特点,在开发动态预测及原始储量计算时应给予高度重视。
5 结论
在进行异常高压气藏研究时应充分考虑储层应力敏感性的影响,掌握储层物性参数随有效应力改变的变化规律。本文建立了渗透率、孔隙度等参数均随有效应力变化的异常高压气藏单相非线性渗流模型;为能准确地计算井底附近压力分布,采用了对数等距网格进行网格剖分,即沿径向向外,网格由密逐渐变稀;采用有限差分法对模型进行离散求解,并创新采用自适应延拓法,克服了传统数值方法要求迭代初值与真解充分接近的局限性。编程计算结果表明,考虑了渗透率、孔隙度等参数随有效应力变化规律的异常高压气藏单相非线性渗流模型是符合工程实际的,自适应延拓法的应用对解决初值问题及奇异问题也是简单有效的。
符号注释:
Φ—当前压力下的孔隙度,%;
Φ0—初始孔隙度,%;
αΦ—孔隙度变化系数;
Δp—有效覆压,MPa;
K—目前压力下的渗透率,μm2;
K0—初始渗透率,;
αK—渗透率变化系数;
μ—天然气黏度,mPags;
p—压力,MPa;
T—绝对温度,K;
V—气体体积,;
R—气体常数,0.008314 MPa·m3/kmol·()K;
ρ—气体密度,kg/m3;
Z—气体偏差因子;
t—时间,d;
P—距离井r处在t时刻的拟压力;
P0—初始拟压力;
q—气井产量,104m3/d;
h—气层厚度,m;
rw—气井半径,m;
re—供给半径,m。
1 Geertsma J.Theeffectof pressure decline on volumetric changes of porous rocks[J].Petroleum Transport AME,1957,210:331-3402 Vairogs J,Hearn CL,Dareing DW,Rhoades VW.Effectof rock stress on gas production from low-permeability from reservoirs[J].Journal of Petroleum Technology,1971,9:1161-1167
3 王江,王玉英.异常高压、特低渗透油藏储层压力敏感性研究[J].大庆石油地质与开发,2003,22(5):28-31.
4 黄继新,彭仕宓,黄述旺,等.异常高压气藏储层应力敏感性研究[J].西安石油大学学报(自然科学版),2005,20(4):21-25.
5 葛家理.油气层渗流力学[M].北京:石油工业出版社,1982.
(修改回稿日期 2013-07-10 编辑 文敏)
郑琴,女,1981年出生,2011年获石油工程计算技术专业博士学位;现在大港油田从事博士后研究。主要研究方向为油气藏数值模拟及优化控制。地址:(300280)天津市大港区大港油田勘探开发研究院歧口开发一室。电话:18622042029。E-mail:zhengqin710@126.com

