基于极大似然估计的加速因子计算方法

郭恒晖,李传日,庞月婵,王开山

(北京航空航天大学可靠性与系统工程学院,北京100191)

基于极大似然估计的加速因子计算方法

郭恒晖,李传日,庞月婵,王开山

(北京航空航天大学可靠性与系统工程学院,北京100191)

目的在产品寿命服从参数未知指数分布的情况下,分析定时转换步加试验得到的数据,估算相关的加速因子。方法列出各应力下的寿命分布密度函数形式,通过加速因子建立各分布密度函数之间的联系,以条件概率的方式处理步加试验每一阶段开始时的累积损伤问题,以极大似然估计的方法进行参数估计。结果得出了一种新的估算加速因子的方法,计算获得了产品在所分析应力下加速因子与应力水平之间的关系。结论利用该方法能很好地处理某应力下无失效发生的情况。

步加试验;条件概率;极大似然估计;加速因子

长寿命、高可靠产品的增多促进了加速试验的发展。加速试验大大地提高了试验效率,与各类其他试验的融合也使得加速试验的应用越来越广泛。在今后的发展中,加速试验仍然是试验发展的重要主题之一。加速寿命试验(ALT)作为一种定性试验在加速试验中占有重要的地位,其主要包括3种类型:恒定应力加速寿命试验(恒加试验)、步进应力加速寿命试验(步加试验)和序进应力加速寿命试验(序加试验)[1—2]。ALT是利用与物理失效规律相关的统计模型对加速条件下获得的失效数据进行转换,得到试件在正常应力水平下寿命特征的试验方法。加速因子是一个关键参数,有效的ALT对加速因子的要求及与失效机理不变条件的关系[3]。由于步进(步退)应力加速寿命试验所需样本量小、试件失效快,在很大程度上节约了试验成本与时间,因而被认为是加速试验的方向[4]。定时截尾试验设置简单,但对于无失效数据的情况又使得计算相当复杂,近年来国内外一些学者对于无故障数据也颇有研究[5—7]。文献[8]在指数分布场合给出了定数截尾样本的统计分析方法,文献[9]则对定数截尾情况下的步加试验数据给出了一种优于文献[8]的统计分析方法。文献[10]假设产品在不同应力下所服从的指数分布不相关,从而对每一个应力下的分布进行假设,将指数分布中的参数θ用2个其他的参数代替,以此来建立不同应力下分布密度函数之间的关系。Nelson根据步加试验各应力间的等效关系提出了一种极大似然的方法来处理有累积损伤的步加试验[11—12]。文献[13]提出了一种在方法、模型未知的情况下直接假设加速因子以求极大似然估计,此方法虽然不受加速模型的限制,但是只能求得2个应力之间的加速因子。

文中利用条件概率来处理步加试验中的累积损伤问题,并结合已有加速模型中加速因子之间的关系,提出了一种关于加速因子新的极大似然估计方法。对于大多数电子产品来说,其寿命都服从指数分布[14],利用条件概率在指数分布下使得计算大为简便。定数截尾试验可以看成是定时截尾试验的特殊形式,文中分析并给出了样本在某一应力无失效情况下的极大似然算法,最后根据文献[15]中关于二极管在电压应力下的步加试验数据,给出计算示例。

1 假设和引理

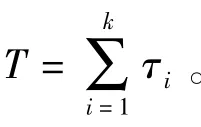
1)产品在正常应力和各加速应力下失效机理不变,且寿命都服从指数分布。

2)加速应力相对于正常应力的加速因子只与应力大小有关,在不同应力下的相对加速因子根据加速模型而关系已知。

3)产品的剩余寿命仅依赖于当时已累积失效部分和当时的应力条件,而与累积方式无关。

利用上面的符号,有:

1)对于步加试验,只有在S1下失效m1j(j=1,…,n1)的失效时间t1j(j=1,…,n1)为寿命数据,其他应力下的失效都是在已有累积损伤之上进行的[1]。

2 理论分析与加速因子的计算

如果没有损伤,则概率密度函数与恒定应力加速试验密度函数的形式类似,再根据引理2)可以推导出对于指数分布在各应力下的概率密度函数分别为:

在步加试验中,从第2步开始所有进行试验的产品都有累积损伤,即τ1时间之后所有发生的失效都是在前一个应力下的试验结束后存活的条件下发生的,设Δ→0+,则以下条件概率可以表示在已知损伤时间的条件下再发生失效的概率:

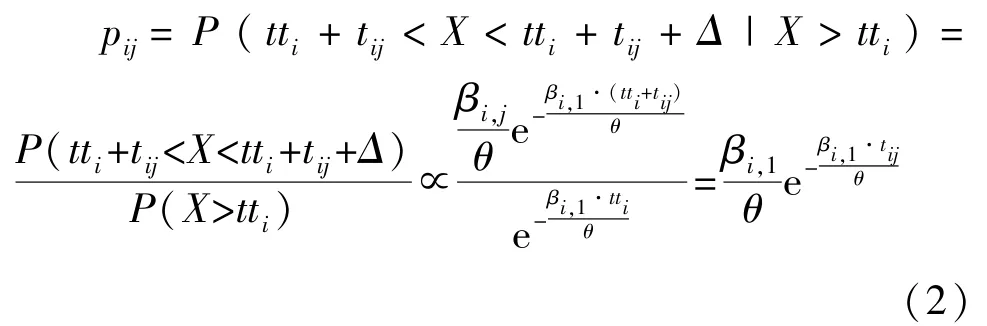
在等效经历tti之后,再经历τi还未失效的概率为:

1)每个试验应力下都有失效。利用加速因子将前各应力下的寿命分布相联系,综合考虑失效数和未失效数,在全样本下的似然函数可以写为:

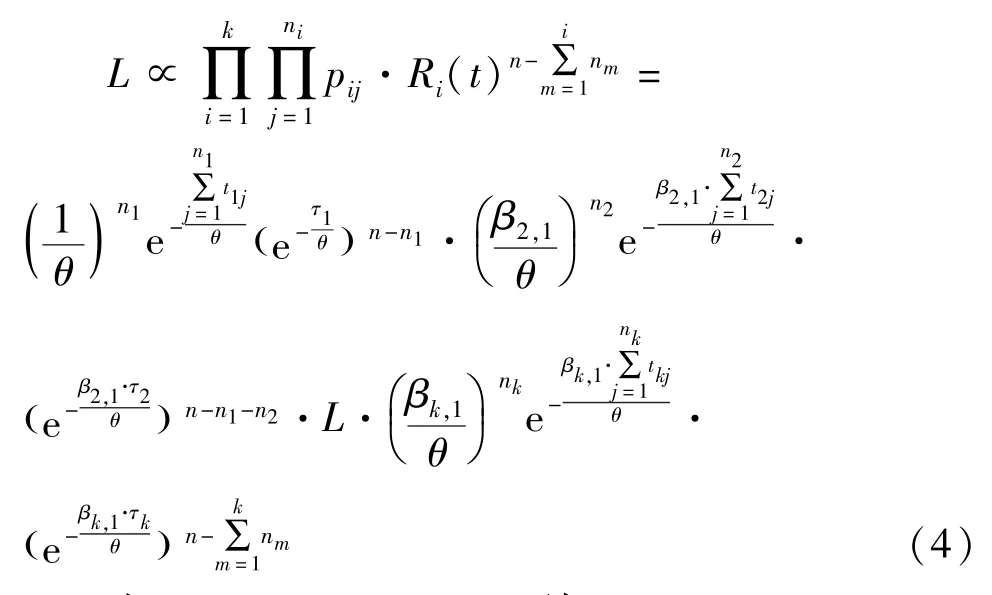
对式(5)取对数,并对θ和x求一阶偏导:

由式(6),再根据不同的加速模型关系φ(Si,Sm,x),便可以计算出参数估计值

2)某一应力下无失效。设在第q(1≤q≤k)阶应力的试验中没有发生失效,在此情况下则只需令:

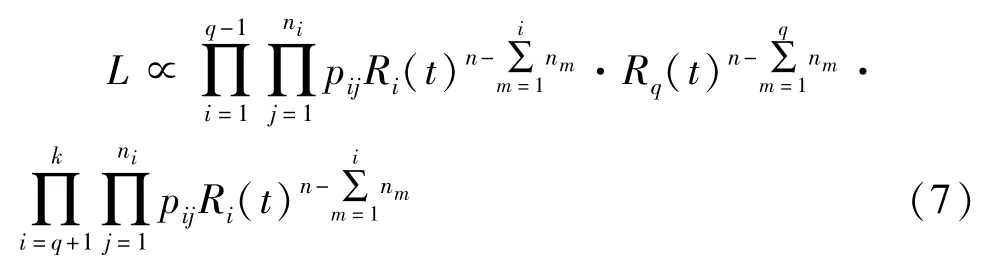
代入相关参数,其他计算方法类似。

3 示例说明

已知某类型二极管寿命服从指数分布,现对样本量为120的该二极管在电压应力下做定时转换步加试验,试验剖面及相关数据见表1[15]。

表1 定时转换步加试验有关数据Table 1 Type-I censored data of SSALT

对于电压应力成熟的加速模型为逆幂律模型:ξ=A·Sx,其中:ξ为某寿命特征;S为电压;A为正常数;x为负常数。

故:

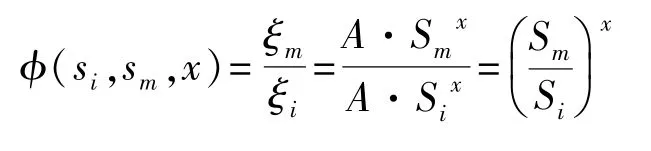
对数似然函数可以写为:

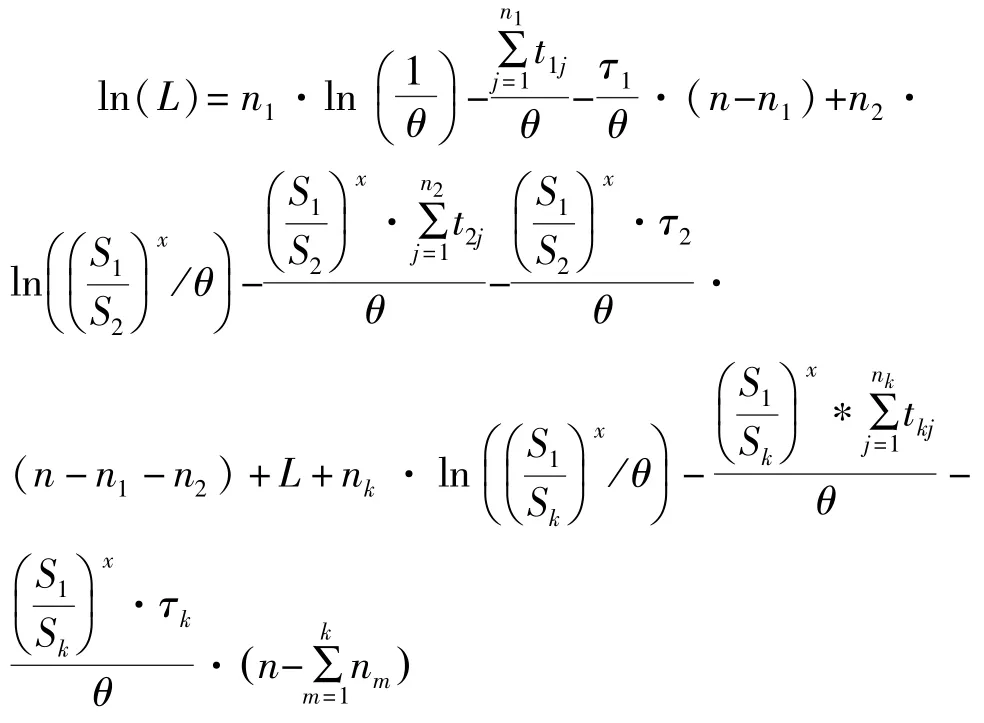
4 结果对比

根据文献[16]中所介绍的CAE技术,采用美国ReliaSoft公司的ALTA软件对第3节中的数据进行比较分析。

输入失效数据以及加速试验应力剖面,选取指数分布下的累积损伤模型(CD指数)。应力转换方式选取逆幂律对数变换。所得计算结果如图1所示。

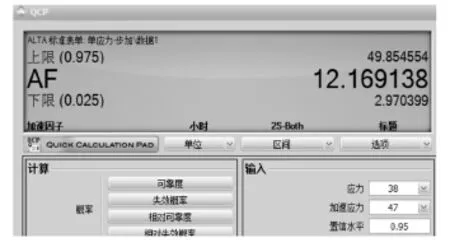
图1 ALT软件计算结果Fig.1 Acceleration factor calculated by ALTA software

由图1可知,该二极管在加速应力47 V下相对于38 V下的加速因子为12.169 138。

5 结语

逐步考虑了在每一种应力下的失效与未失效的情况,将步加试验中的每一步试验看成一个独立体,以条件概率的方法处理每一步进行试验的产品的累积损伤问题。利用此关系建立极大似然方程,根据各应力下加速因子的关系,提出一种关于加速因子的新的极大似然估计方法,给出了某应力无失效情况的计算处理方法。另外此方法根据全样本数据适用于变应力加速寿命试验的情况,还可以推广到威布尔分布与对数正态分布,同时令τi=ti,ni即可以适用于定数截尾。

[1] 茆诗松,王玲玲.加速寿命试验[M].北京:科学出版社,1997. MAO Shi-song,WANG Ling-ling.Accelerated Life Testing [M].Beijing:Science Press,1997.

[2] 张志华.加速寿命试验及其统计分析[M].北京:北京工业大学出版社,2002. ZHANG Zhi-hua.Accelerated Life Testing and Statistical Analysis[M].Beijing:Beijing University of Technology Press,2002.

[3] 杨宇航,周源泉.加速寿命试验的理论基础[J].推进技术,2001,22(4):276—278. YANG Yu-hang,ZHOU Yuan-quan.Theoretical Foundation of Accelerated Life Testing[J].Journal of Propulsion Technology,2001,22(4):276—278.

[4] 陈文华,杨帆,刘俊俊,等.步进应力加速寿命试验方案模拟评价理论与方法[J].机械工程学报,2012,48 (22):176—188. CHEN Wen-hua,YANG Fan,LIU Jun-jun,et al.Theory and Method for Simulation Evaluation of Accelerated Life Test Plan under Step-stress[J].Journal of Mechanical Engineering,2012,48(22):176—188.

[5] 张晓冉,胡文杰,夏茂辉.分组定时截尾无失效数据的迭代Bayes分析[J].工程数学学报,2009,26(2): 265—272.ZHANG Xiao-ran,HU Wen-jie,XIA Mao-hui.Iterative Bayes Analysis of the Grouped Timing Terminated and Zero-failure Data[J].Chinese Journal of Engineering Athematics,2009,26(2):265—272.

[6] 韩明.无失效数据情形失效率的综合估计[J].高校应用数学学报A辑,2002,17(2):200—206. HAN Ming.Synthetic Estimation of Failure-rate in the Case of Zero-failure Data[J].Appl Math J Chinese Univ Ser A,2002,17(2):200—206.

[7] 张志华.无失效数据的统计分析[J].数理统计与应用概率,1995,10(1):94—101. ZHANG Zhi-hua.Statistical Analysis about Zero-failure Data[J].Mathematical Theory and Applied Probability, 1995,10(1):94—101.

[8] 茆诗松.指数分布场合下步进应力加速寿命试验的统计分析[J].应用数学学报,1985,8(3):311—316. MAO Shi-song.Statistical Analysis of Accelerated Life Testing-step-stress Models under the Exponential Distribution Case[J].Acta Mathematicae Application Sinica, 1985,8(3):311—316.

[9] 仲崇新,张志华.指数分布场合定时和定数截尾步进应力加速寿命试验和统计分析[J].应用概率统计, 1991,7(1):52—59. ZHONG Chong-xing,ZHANG Zhi-hua.Statistical Analysis of Types I and II Censoring Data from Step-stress Accelerated Life Testing Models under the Exponential Distribution[J].Chinese Journal of Applied Probability and Statiatics,1991,7(1):52—59.

[10]费鹤良,张学新.指数分布场合下步进应力加速寿命试验的极大似然估计[J].应用数学,2004,17(3): 398—404. FEI He-liang,ZHANG Xue-xin.Maximum Likelihood Estimate of Step-stress Accelerated Life Testing under the Exponential Distribution[J].Mathematical Applicata, 2004,17(3):398—404.

[11]NELSON W B.Accelerated Life Testing Step-stress Models and Data Analyses[J].Transactions of Reliability, 1980,29(2):103—108.

[12]NELSON W B.Accelerated Testing-statistical Models,Test Plans and Data Analysis[M].New Jersey:John Wiley& Sons Inc,2004.

[13]ISMAIL A A.On Designing Step-stress Partially Accelerated Life Tests under Failure-censoring Scheme[J].Risk and Reliability,2013,227(6):662—670.

[14]姜同敏,王晓红.可靠性与寿命试验[M].北京:国防工业出版社,2012. JIANG Tong-min,WANG Xiao-hong.Reliability and Life Test[M].Beijing:Defense Industry Press,2012.

[15]郭峻.对步进应力加速寿命试验的实施和讨论[J].应用概率统计,1998,4(3):327—330. GUO Jun.Implementation and Discussion of Step-stress Accelerated Life Testing[J].Applied Probability and Statistics,1998,4(3):327—330.

[16]周新建,万正平,周长国.基于ALTA的加速寿命试验数据分析[J].华东交通大学学报,2007,24(5):107—109. ZHOU Xin-jian,WAN Zheng-ping,ZHOU Chang-guo.Accelerated Life Test Data Analysis Based on ALTA[J]. Journal of East China Jiaotong University,2007,24(5): 107—109.

Calculation of Acceleration Factor Based on Maximum Likelihood Estimation

GUO Heng-hui,LI Chuan-ri,PANG Yue-chan,WANG Kai-shan
(Reliability and System Engineering Institute,Beihang University,Beijing 100191,China)

Objective To estimate the associated acceleration factor by analyzing the Trial data of step-stress accelerated life tests(SSALT)with Type-I censored data,assuming the lifetime of products followed exponential distribution.Methods Lifetime distribution density functions under different stresses were listed.Linkages were established between the distribution density functions by acceleration factors(AF).And then conditional probability distribution was used to deal with the problem of cumulative damage at the beginning of each stage by stepwise analysis of the testing.The AFs were estimated by maximum likelihood estimation.Results The paper offered a new method to deal with the cumulative damage. The relationship between AFs and stress levels under the tested stress was calculated.Conclusion It is a feasible method to cater the situation that no failure occurs under certain stress.

step-stress accelerated life testing;conditional probability;maximum likelihood estimation;acceleration factor

LI Chuan-ri(1964—),Male,Professor&Researcher,Research focus:product environmental engineering and reliability test technology.

10.7643/issn.1672-9242.2014.05.010

TB114.3

:A

1672-9242(2014)05-0049-05

2014-05-14;

2014-05-25

Received:2014-05-14;Revised:2014-05-25

郭恒晖(1989—),男,安徽六安人,硕士研究生,主要研究方向为产品环境与可靠性试验。

Biography:GUO Heng-hui(1989—),Male,from Liuan,Anhui,Master graduate student,Research focus:environmental and reliability test.

李传日(1964—),男,教授,研究员,主要研究方向为产品环境工程、可靠性试验技术。