基于HHT方法的公路运输振动信号时频分析
颜诗源,李新俊,吴勋,张仕念,何敬东
(北京市海淀区北清路109号203分队,北京100094)
基于HHT方法的公路运输振动信号时频分析
颜诗源,李新俊,吴勋,张仕念,何敬东
(北京市海淀区北清路109号203分队,北京100094)
目的分析具有非线性、非平稳特征的公路运输振动信号的时频信息。方法利用Hilbert-Huang变换算法,在对公路运输的振动信号进行EMD分解的基础上,开展Hilbert谱和各IMF的功率谱密度计算,并与常规的功率谱进行比较。结果基于IMF分量的功率谱可以克服传统Fourier功率谱计算在低频偏低、高频偏高的误差。结论基于HHT的公路运输振动信号时频分析方法是一种有效的运输振动非平稳信号分析手段。
振动功率谱;Hilbert-Huang变换;时频分析
在振动信号的处理和归纳中,一般都将其近似作为线性平稳信号,如GJB/Z 126—99振动、冲击环境测量数据归纳方法[1]、GJB/Z 222—2005动力学环境数据采集和分析指南[2]等,以及采用Bootstrap方法[3]。真实的振动信号不可避免地存在非线性和非平稳性,在传统的以Fourier变换为基础的功率谱密度(PSD)振动载荷谱分析方法中的线性平稳假设,往往在低频幅值偏低,而在高频部分偏高[4—5]。其他常用的非平稳随机信号处理方法亦存在不足,如短时 Fourier变换要求信号具有不变的分析带宽[6],小波分析需要选定小波基函数、自适应差[7]。
1 Hilbert-Huang谱
1.1Hilbert-Huang变换
Norden E.Huang等人在提出经验模态分解的(Empirical Mode Decomposition,EMD)基础上,对EMD分解得到的IMF进行Hilbert谱分析,该方法被称为Hilbert-Huang变换,即HHT。HHT首先利用EMD方法将信号分解为IMF,然后对每一个IMF进行Hilbert变换,得到对应的Hilbert谱,最后汇总所有IMF的Hilbert谱得到原始信号的Hilbert谱。该方法利用EMD将信号中不同尺度的波动或趋势逐级分解开来,基于这些分量进行的Hilbert变换可以反映信号能量在空间(或时间)各种尺度上的分布规律。该方法被认为是处理非平稳信号的有力工具之一。
HHT首先对信号进行EMD处理,得到信号的IMF及残差。EMD分解的思路是:对一原始信号x(t),利用三次样条函数曲线插值的方法找出其上、下包络及包络的均值曲线m(t),如果x(t)与m(t)之差h(t)不满足IMF分量的条件,则将h(t)视为新的原始信号,继续进行前述分解,直到找到本阶的IMF,记为c(t)。重复计算,可以将x(t)分解为多个IMF分量ci(t)和残差r(t)之和:

对上述IMF分量ci(t)进行Hilbert变换,即可得到每个IMF分量的瞬时频谱,综合所有IMF分量的瞬时频谱就可得到一种新的时频描述方式,即Hilbert谱。Hilbert变换是一种线性变换,它强调局部性质,由它得到的瞬时频率是最好的定义,避免了Fourier变换产生的许多事实上不存在的高、低频成分,具有直观的物理意义。ci(t)的Hilbert变换为:
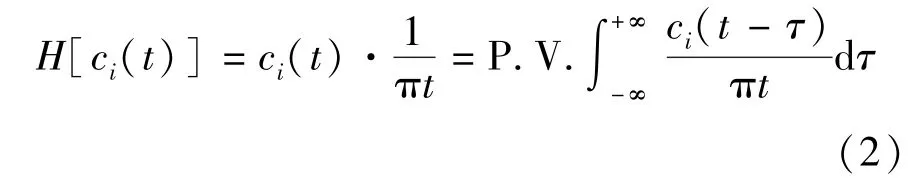
其中P.V.表示柯西主值积分。构造ci(t)的解析信号为:


如果直接对信号x(t)进行整体Hilbert谱分析,可以表示为:

式(6)表达了信号x(t)联合的时频变化关系。根据式(5)和(6),可以得到x(t)的Hilbert谱:

式(7)描述的Hilbert谱可看作是一种加权的联合幅值-频率-时间三维谱。又定义Hilbert边际谱为:
综合灌浆法:钻机对中调平固定→开孔钻至第一段→阻塞洗孔、压水及灌浆→钻至终孔段→一次性洗孔、压水→自下而上分段灌浆至第二段→封孔。

在式(8)的Hilbert边际谱中,在某一频率上存在着能量就意味着具有该频率的振动存在的可能性,具有该频率的波在信号整个持续时间内的某一时刻出现了,而该振动出现的具体时刻在Hilbert谱中给出。
定义Hilbert能量谱为:

在分析中,可能只对某些频率范围内的信号感兴趣,即对某几个IMF分量的组合进行Hilbert变换,结果成为局部Hilbert谱。
1.2 Hilbert-Huang谱与Fourier功率谱的比较
对解析信号zi(t)两边做Fourier变换,可以得到:


典型的Fourier功率谱的定义为:设x(t)为一平稳随机过程,若其自相关函数Rxx(τ)的傅立叶变换存在,即:

则称Sxx(ω)为x(t)的功率谱密度,ω为频率。在工程中多用频率f作为功率谱密度的自变量,这时有下面关系成立:

另外由于工程上负频率无意义,往往使用单边谱密度,其定义为:
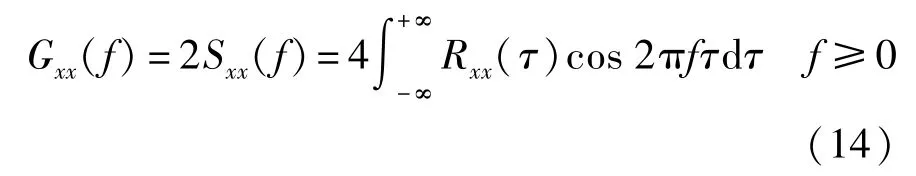
功率谱密度描述了随机振动的频率结构,从物理意义角度上看,它是随机振动的能量按频率分析的度量,功率谱密度曲线下方的面积即为随机信号的均方值,即:

对比式(8)、式(11)和式(14)可以看出,由于IMF分量ci(t)是原始信号的某一个包络,其幅值大于对应的原始信号,因而计算边际谱的幅值与Fourier功率谱幅值是不一致的。
2 公路运输振动数据分析
公路运输的振动响应一般随运输平台、公路路面等级、运输平台速度等不同而有一定差异。为了获取真实有效的振动响应数据,需要通过设计采集试验,获取在特定路面等级和运输速度组合下一定时间长度的振动数据。文中利用LMS振动采集系统,以400 Hz的采样率,在不同的路面等级下以不同的速度,采集匀速运动的卡车上的产品振动情况。以某点位Z方向的振动为例,其一段时域波形如图1所示。
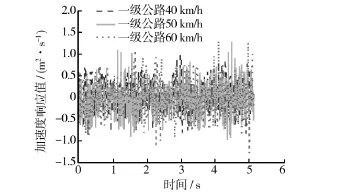
图1 不同速度下振动时域Fig.1 Time domain waveform at different velocity
以其中一级公路40 km/h的振动信号为例,计算其HHT谱与边际谱,分别如图2和图3所示。
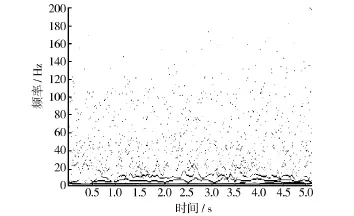
图2 HHT谱Fig.2 HHT spectrum

图3 HHT边际谱Fig.3 HHT marginal spectrum
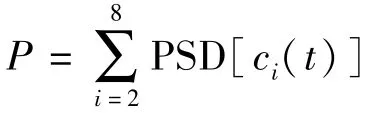
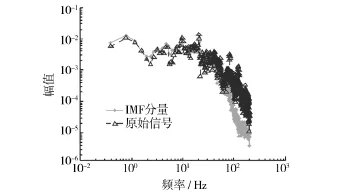
图4 IMF分量与原始信号的PSD对比Fig.4 PSD comparison between IMF component and the original signal
从图4中可以看出,IMF分量中剔除了最高频的c1(t)及残差,基于IMF分量的在低频部分有所加强,而在高频部分得到了抑制。显然,该计算对传统功率谱密度计算中“低频幅值偏低,高频部分偏高”进行了有效修正。对比图3与图4,边际谱的频率与功率谱的频率峰值点基本是一致的,表示边际谱对信号能量特征的识别度较好。图2能反映出信号的时间-频率信息。
3 结语
文中对公路运输的振动信号引入HHT分析方法,对其进行经验模态分解,得到各阶IMF分量。通过对IMF分量与原始信号的Fourier功率谱分析,结果表明,通过合理选择IMF分量的范围,可以克服传统功率谱分析针对非平稳信号处理中低频偏低、高频偏高的误差。同时,振动信号的HHT边际谱频率与Fourier功率谱在统计意义上频率具有较好的拟合度,表明边际谱对随机振动信号的频率分辨度较好。采用HHT方法对公路运输振动信号进行分析处理,是一种有效的振动特征提取方法。
[1] GJB/Z 126—99,振动、冲击环境测量数据归纳方法[S]. GJB/Z 126—99,The Inductive Methods for Environmental Measured Data of Vibration and Shock[S].
[2] GJB/Z 222—2005,动力学环境数据采集和分析指南[S]. GJB/Z 222—2005,Guidelines for Dynamic Environmental Data Acquisition and Analysis[S].
[3] 张建军,孙建勇,常海娟.Bootstrap方法在小样本随机振动环境测量数据归纳中的应用研究[J].装备环境工程,2013,10(5):70—76,80. ZHANG Jian-jun,SUN Jian-yong,CHANG Hai-juan.Application Research of Bootstrap Method in Small Sample Measured Data Reduction of Random Vibration[J].E-quipment Environmental Engineering,2013,10(5):70—76,80.
[4] 赵杨,武岳,曹曙阳,等.利用HHT方法对非平稳风力的时频分析[J],振动与冲击,2011,30(2):5—9. ZHAO Yang,WU Yue,CAO Shu-yang,et al.Time Frequency Analysis of a Non-stationary Wind Pressure with HHT Method[J].Journal of Vibration and Shock,2011, 30(2):5—9.
[5] 朱玉琴,肖勇,苏艳.装甲平台诱发环境振动数据处理技术与应用研究[J].装备环境工程,2013,10(3): 72—76. ZHU Yu-qin,XIAO Yong,SU Yan.Application Research of Vibration Data Processing Technology for Armed Vehicle Platform Induced Environment[J].Equipment Environmental Engineering,2013,10(3):72—76.
[6] 胡广书.数字信号处理理论、算法与实现[M].北京:清华大学出版社,2003. HU Guang-shu.Digital Signal Processing,Theory,Algorithm and Implementation[M].Beijing:Tsinghua University Press,2003.
[7] ANTONIADIS A,OPPENHEIM G.Wavelets and Statistics(Lecture Notes in Statistics)[M].Berlin:Springer Verlag,1995.
[8] HUANG Norden E,SHEN Zheng,LONG Steven R,et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis[J].Proc R Soc Lond,1998,454:904—993.
Frequency Analysis for Vibration Signal from Road Transportation Using HHT
YAN Shi-yuan,LI Xin-jun,WU Xun,ZHANG Shi-nian,HE Jing-dong
(Division 203,No.109 Beiqing Road,Haidian,Beijing 100094,China)
Objective To study the time-frequency character of the vibration signal from road transportation which is nonlinear and non-stationary.Methods Using the Hilbert-Huang transformation algorithm,the vibration signal from road transportation was firstly decomposed by the EMD method,based on which its Hilbert spectrum and the power spectral density were calculated and compared to the traditional Fourier power spectral density.Results The power spectral density of the IMFs can overcome the error of low value in low frequency and high value in high frequency by the traditional Fourier method.Conclusion The HHT algorithm is a powerful method to analyze the time-frequency character of the nonlinear nonstationary vibration signal from road transportation.
vibration power spectrum;Hilbert-Huang transformation;time-frequency analysis
10.7643/issn.1672-9242.2014.05.005
TP311
:A
1672-9242(2014)05-0023-04
2014-06-05;
2014-06-22
Received:2014-06-05;Revised:2014-06-22
颜诗源(1981—),男,湖南人,博士,助理研究员,主要从事可靠性、环境等方面的研究。
Biography:YAN Shi-yuan(1981—),Male,from Hunan,Doctor,Assistant researcher,Research focus:reliability&environment.

