基于指数伤害模型的砂岩酸化模拟
刘平礼薛 衡李年银罗志锋邢希金山金成
(1.油气藏地质及开发工程国家重点实验室·西南石油大学,四川成都 610500;2.中海石油研究总院,北京 100027 ;3.中海石油(中国)有限公司天津分公司,天津 300452)
基于指数伤害模型的砂岩酸化模拟
刘平礼1薛 衡1李年银1罗志锋1邢希金2山金成3
(1.油气藏地质及开发工程国家重点实验室·西南石油大学,四川成都 610500;2.中海石油研究总院,北京 100027 ;3.中海石油(中国)有限公司天津分公司,天津 300452)
在两酸三矿物模型及精细化模型基础上建立了符合地层尺度的砂岩基质酸化径向非均质流动反应数学模型。为了研究伤害带孔、渗分布差异对酸化模拟效果的影响,将伤害带渗透率合理地假设为指数型分布。通过将伤害带孔、渗分布常规模型与指数模型分别引入径向非均质流动反应模型中,重点讨论了不同伤害带假设对酸化模拟效果的影响。模拟发现,前者酸化后地层孔隙度沿径向呈递减规律;而后者酸化后地层孔隙度沿径向呈递增规律,径向上孔隙度起伏更为平缓,说明伤害带内渗流条件得到了均匀改善,其结果更符合真实情况。在相同注入条件下,指数模型较常规模型计算的酸化效果更显著,同时大排量有利于增加酸液深穿透距离,但与小排量相比,其酸化后的油井增产倍比相当。
砂岩;基质酸化;酸岩反应;伤害模拟;数学模型;数值模拟
砂岩酸化模型对砂岩酸化设计及酸化效果预测至关重要,Schechter和Gidley自1969年首次提出了毛细管模型以表征砂岩酸化模拟过程以来[1],国内外学者从微观及宏观上深入研究了砂岩酸化反应机理,并取得了重大进展与突破。微观上,William和Whiteley在毛细管模型基础上建立了慢反应模型[2],Hill等提出了改进毛细管模型[3]。宏观上,Labrid和Lund相继提出了砂岩酸化动力学模型和基于酸—岩反应模型的集总参数模型[4-5]。1980年Hekim提出的分布参数模型弥补了集总参数模型的不足[6],而Taha在其基础上最终提出了目前国内外普遍推崇的非均质模型[7]。Taha非均质模型中将矿物划分为2大类:硅酸盐类和石英类,同时考虑了Si(OH)4沉淀对孔隙度的堵塞。另外,Taha还考虑了地层径向上的渗透率变化,并且将油气藏沿垂向上划分为不同小层,间接引入了地层垂向上的渗透率变化。Bryant改进了以往的砂岩酸化模型,其模拟结果与室内实验结果拟合度非常高,可为现场施工提供可靠参考依据[8]。
近年来,国内外学者在以往模型基础上做了大量研究与改善。2000年,Quinn等通过模拟求解地球化学模型,深入研究分析了影响砂岩酸化效果的关键因素[9]。同年,Nguyen建立了低渗透砂岩油藏基质酸化三维模型,并建立了矿物浓度与孔隙度间的关系模型[10]。2003年Rodoplu、Hill 等通过室内实验研究砂岩酸化时形成蚓孔的条件并建立了理论模型[11]。2004年Li等提出一种符合线性流规律的精细化模型,但其忽略了周向上的酸液流动反应过程[12]。2005年,Xie等在Rodoplu基础上进一步研究了砂岩酸化中蚓孔形成机理[13]。2006年Jianbo Zou等提出了新的砂岩基质酸化表皮系数实时监测方法[14]。2012年LI Songyan在广义分布模型基础上建立了实际现场酸化时的酸岩反应数学模型[15]。虽然最早Taha就在非均质模型中假设了地层渗透率的非均质性,而且,在此之后许多改进的酸—岩反应数学模型中也做了类似假设,但是具体如何合理地假设渗透率沿地层径向上的非均匀分布没做过详细讨论。笔者在新建模型基础上合理假设了伤害带渗透率沿径向呈指数型分布,最终通过编程求解了该模型,并与常规模型模拟结果做了对比分析。
1 数学模型的建立
1.1 渗透率指数分布模型
由试井和测井取得的污染半径rd和表皮系数S资料,计算地层渗透率沿井眼径向的非均质数值分布。
由等值渗流阻力法有
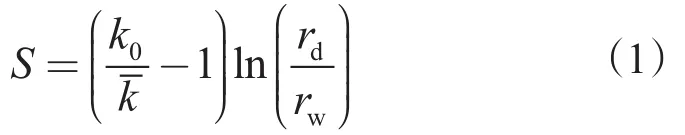
假设伤害带为指数污染模型,沿径向滤饼区和过渡带的渗透率按指数规律递减[16]
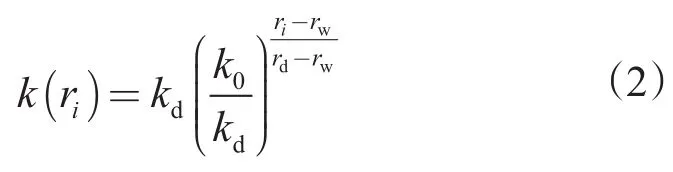
伤害带平均渗透率
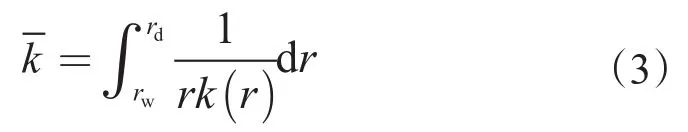
以井壁rw处为初始节点,将伤害带范围内划分为n个单元体,各节点满足ri+1/ri=a,a是等比例系数(取值为1.1)。
则式(3)通过梯形公式化简得到
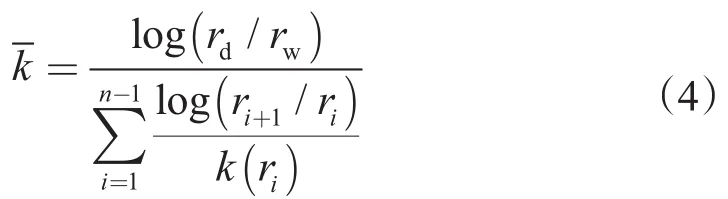
结合式(1)、(2)、(4)式计算得到
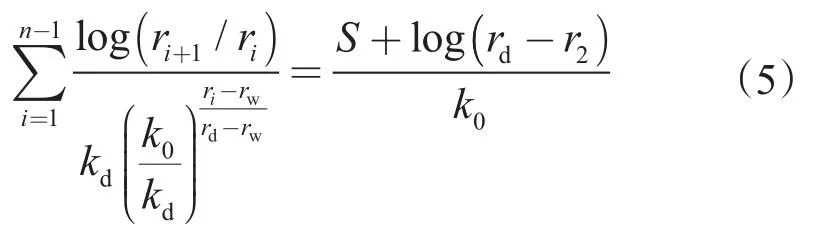
假设误差系数ε等于0.01,对(5)式采用二分法编程求解得到井壁处污染后渗透率kd。最终,将ri及kd带入(2)式求取地层渗透率沿径向的指数分布,如图1。
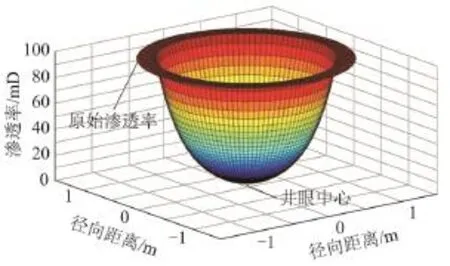
图1 渗透率指数分布图
1.2 流动反应数学模型
根据物质平衡方程建立了符合现场砂岩酸化施工的径向流动模型及酸化模型,假设条件如下:(1)酸液在孔隙介质中的流动为径向流;(2)酸化层位为各向同性非均质储层,忽略裂缝及孔洞介质;(3)孔隙度的非均质性与矿物学之间无关联;(4)忽略酸液的分子扩散作用;(5)岩石矿物分为快速反应矿物和慢速反应矿物,两种酸液与3种矿物的反应分别按各自的动力学方程进行。
流速方程
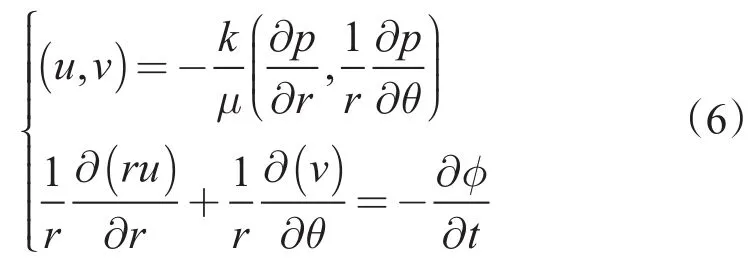
HF酸浓度方程
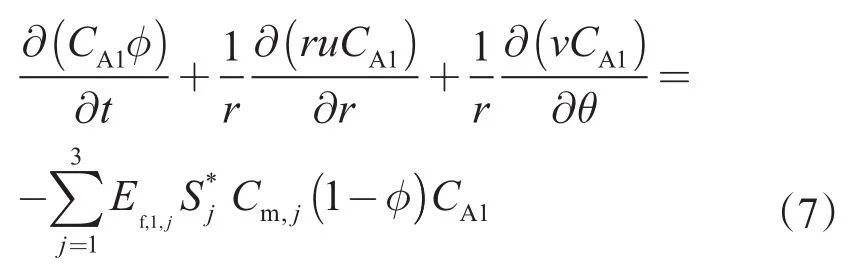
H2SiF6浓度方程
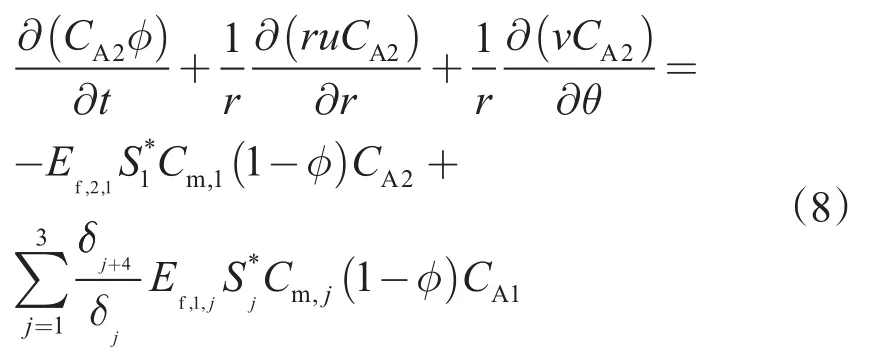
快反应矿物浓度方程
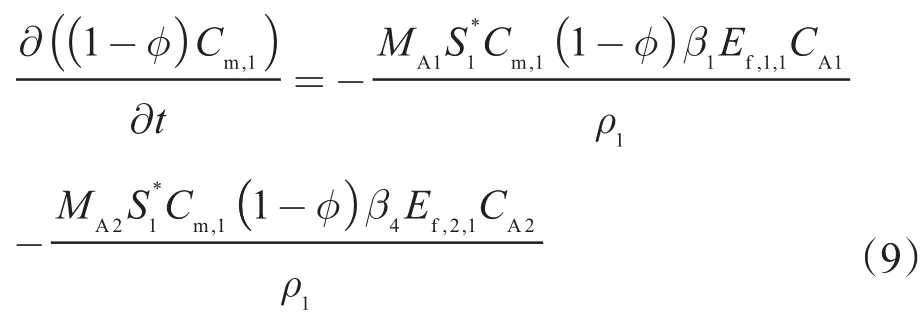
慢反应矿物浓度方程
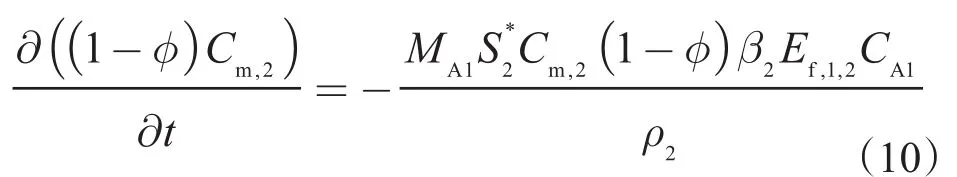
硅胶沉淀浓度方程
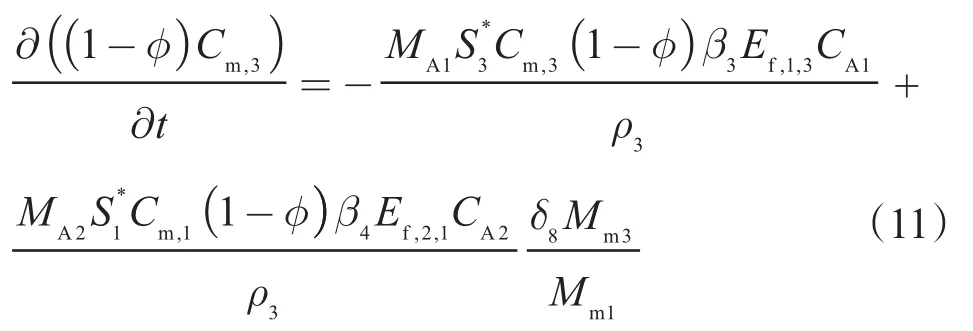
孔隙度方程
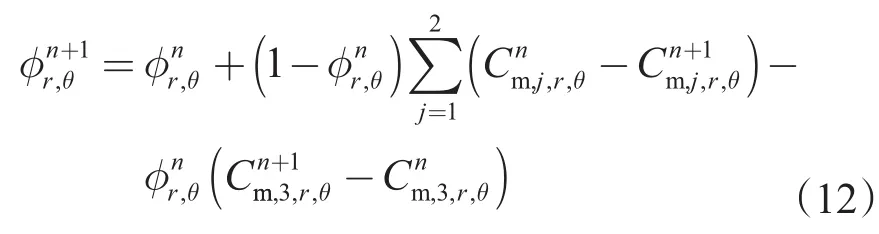
1.3 定解条件
初始条件,t=0时刻的初始值
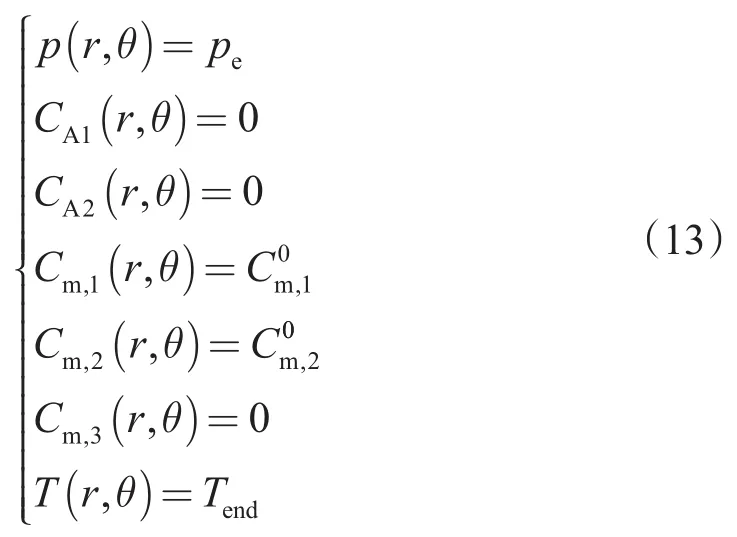
压力边界条件
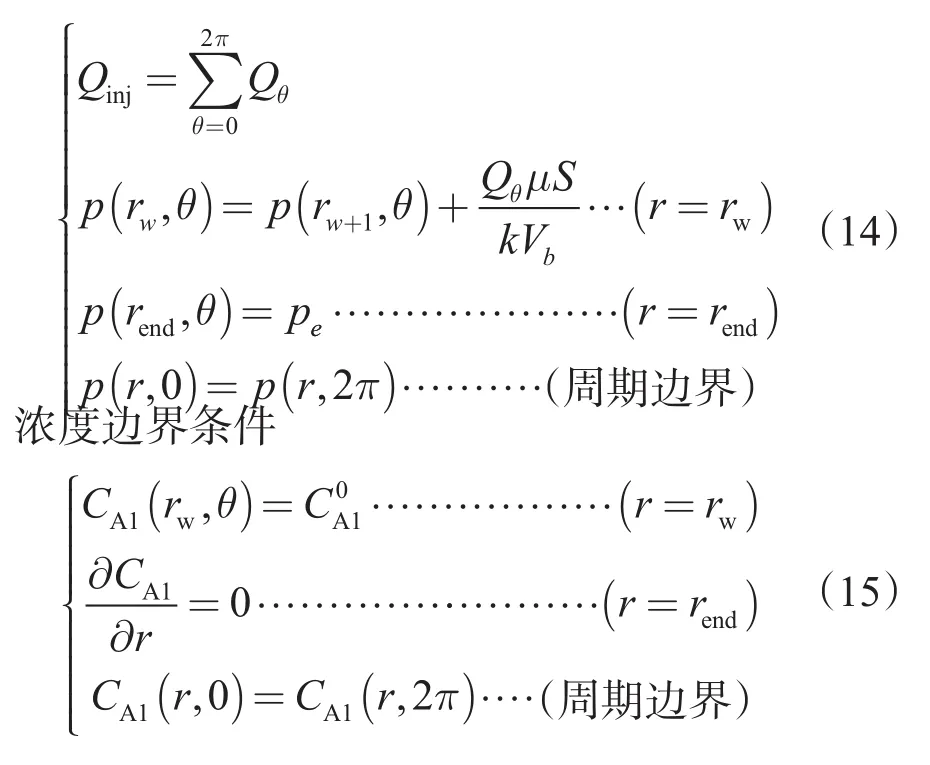
2 算例分析
地层物性参数及酸化工艺参数见表1。

表1 地层物性参数及酸化工艺参数
常规模型中,伤害带孔、渗为算术平均值,此时酸化前后地层孔隙度分布如图2(a);指数模型中,伤害带孔、渗呈指数分布,其对应的酸化前、后地层孔隙度分布如图2(b)。图2(a)与图2(b)对比分析表明,虽然酸化后地层孔隙度都取得了不同程度的改善,但是不同伤害模型所计算的孔隙度大小和分布规律差异显著。显然,指数模型计算结果更符合真实情况,酸化后,其伤害带孔隙度基本恢复至地层原始孔隙度,最终达到恢复产能的目的。
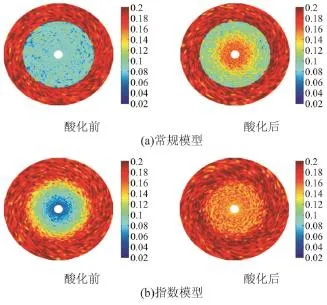
图2 酸化前后地层孔隙度二维分布
相同注入条件下持续注液60 min,酸化前、后伤害带孔隙度沿地层径向分布规律如图3。采用常规模型计算时,由于越靠近井壁处,酸与岩石矿物作用时间越长,其溶蚀程度也相应更强,因此在酸化后,越靠近井壁处的位置,其孔隙度越大,其中井壁处的孔隙度值改善最大,从酸化前的0.085升至酸化后的0.17,如图3(a)。而采用指数模型计算时,由于越靠近井壁处地层伤害越严重,因此酸化前的伤害带孔隙度沿地层径向呈递增规律,受其影响,酸化后的伤害带孔隙度沿地层径向仍为递增曲线,如图3(b)。
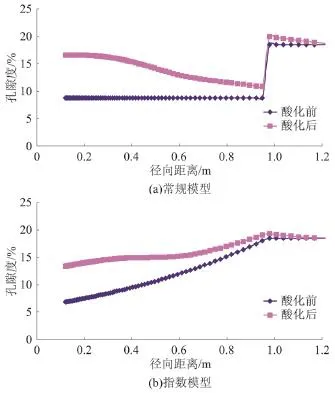
图3 酸化前后地层孔隙度径向关系曲线
表2是常规模型与指数模型酸化效果对比结果,虽然两者酸化有效作用距离相同,但增产倍比、表皮系数及平均渗透率等计算结果值具有一定差异。相同注入条件下,指数模型比常规模型酸化效果更显著。
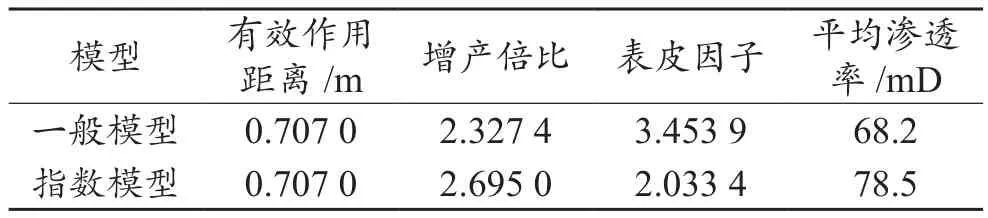
表2 常规模型与指数模型模拟结果对比
图4是注处理液60 min时的酸浓度及矿物浓度沿地层径向分布曲线。从图4中可知,HF酸在流向远井带过程中不断与可溶岩石矿物(快反应矿物M1、慢反应矿物M2和硅胶矿物M3)间发生不同程度的溶蚀反应,削弱了HF酸浓度,最终,受注入速度、注酸量及储层厚度等因素影响,HF酸的有效作用距离为0.7 m。H2SiF6酸浓度沿径向方向先增后减,其峰值在0.7 m附近。快反应矿物浓度M1沿地层径向呈先降低再升高的趋势,最终恢复到初始浓度。这主要是受酸液浓度、酸—岩接触时间、地层温度等诸多因素共同作用的结果,而在伤害带,硅胶矿物M3的生成不利于地层渗透率的改善和恢复,如果不考虑硅胶沉淀,伤害带平均渗透率将从78.5 mD上升到85.2 mD,提高了6.7%。
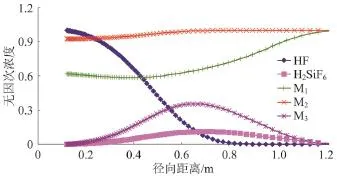
图4 注处理液60 min时酸浓度及矿物浓度沿地层径向分布曲线
从图5可以看到,随着注液时间的延长,纵向上地层孔隙度逐步增大,注液10 min、30 min、60 min和120 min时所对应的井壁处孔隙度分别为0.085、0.105、0.132和0.171;横向上酸化作用距离随注液时间不断增加,注液10 min、30 min、60 min和120 min时所对应的酸液穿透距离分别为0.5 m、0.8 m、1 m和1.2 m。在注液120 min后,伤害带孔隙度基本恢复至地层原始孔隙度。
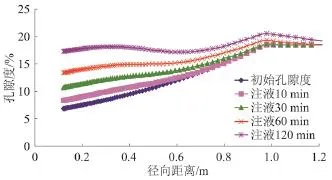
图5 相同排量不同时间孔隙度沿地层径向分布曲线
图6是不同排量下注液60 min后的孔隙度沿地层径向分布曲线。小排量条件下,由于酸—岩反应占主导作用,酸液大多消耗在井眼周围,因此,0.5 m3/min排量下所对应的井壁处孔隙度最大,为0.145;而大排量条件下,由于流速起主导作用,部分酸液还未来得及反应就流向远端,从而使得酸液穿透距离更远,2 m3/min排量下所对应的酸液穿透距离最大,超过1.2 m。因而在低于地层破裂压力条件下尽量提高注入排量有利于增加酸液深穿透距离。
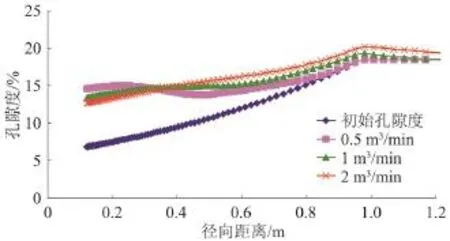
图6 不同排量下注液60 min后孔隙度沿地层径向分布曲线
从图7可以看出,注处理液初期,表皮因子迅速下降,在注液前30 min表皮因子从18降到了3,下降了83.3%。随着注液时间增加,表皮因子趋于平缓,在30~60 min内表皮因子只降低了11.1%,此时表皮因子累计降低94.4%,地层伤害基本得到解除。随着表皮因子不断降低,油层增产倍比逐渐提高,同样,随着注液时间延长,增产倍比增加幅度趋于平缓,注液60 min内,增产2.7倍。
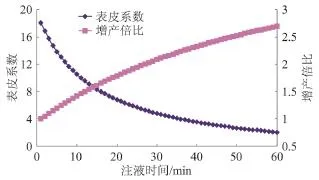
图7 表皮因子及增产倍比随时间变化
3 结论与建议
(1)在两酸三矿物模型及精细化模型基础上建立了更为符合现场酸化施工的径向非均质模型,以径向非均质模型为基础,讨论了不同伤害带孔、渗分布规律对酸化效果的影响,通过模拟结果对比分析发现:指数模型计算结果更符合真实情况;在相同注入条件下,常规模型较指数模型计算的酸化效果更弱。
(2)以指数模型基础进行酸化模拟研究,研究表明:大排量有利于增加酸液深穿透距离,随着注液时间的延长,纵向上地层孔隙度逐步得到改善,横向上酸化作用距离不断向远井带推移;酸化过程中,表皮系数、增产倍比及平均渗透率随时间延长逐渐趋于平缓。
(3)径向非均质模型同样适用于地层尺度下的各向异性非均质地层酸化模拟研究,下一步将开展地层温度、注酸排量、酸液浓度等因素对各向异性非均质砂岩储层酸化类蚓孔结构的酸化模拟研究。
符号说明
CA1为HF酸浓度,kmol/m3;CA2为H2SiF6酸浓度,kmol/m3;Cm,1为快反应矿物体积分数,无因次;Cm,2为慢反应矿物体积分数,无因次;Cm,3为硅胶矿物体积分数,无因次;Ef,1,1为HF酸与快反应矿物的反应速度常数,m/s;Ef,1,2为HF酸与慢反应矿物的反应速度常数,m/s;Ef,1,3为HF酸与硅胶矿物的反应速度常数,m/s;Ef,2,1为H2SiF6酸与快反应矿物的反应速度常数,m/s;为伤害带平均渗透率,D;k0为地层原始渗透率,D;kd为井壁处伤害后渗透率,D;k为地层渗透率,D;MA1为HF酸相对分子质量,g/mol;MA2为H2SiF6酸相对分子质量,g/mol;pe为原始地层压力,MPa;p为地层压力,MPa;Qinj为注酸排量,m3/min;Qθ为井壁处各网格节点的酸流量,m3/min;rd为伤害半径,m;rend为径向上最后一个网格节点距井壁的距离,m;rw为井眼半径,m;r为极坐标轴的径向距离,m;S1~3*为比表面,m2/m3;S为表皮因子,无量纲;Tend为原始地层温度,K;T为地层温度,K;u为r方向上流速,m/ s;Vb为微元体中θ-z渗流界面面积与Δr之比,m;v为θ方向上流速,m/s;β1~4为溶蚀能力数,kg/kg;δ1~8为化学计量系数,无因次;Δt为时间步长,s;θ为极坐标轴角度,°;μ为酸液黏度,mPa·s;ρ1为快反应矿物密度,kg/m3;ρ2为慢反应矿物密度,kg/m3;ρ3为硅胶矿物密度,kg/m3;φ为地层孔隙度,无因次。
[1]SCHECHTER R S,GIDLEY J L.The change in pore size distribution from surface reactions in porous media[J].AIChE Journal,1969,15(3):339-350.
[2]WILLIAMS B B,WHITELEY M E.Hydrofluoric acid reaction with a porous sandstone[J].Old SPE Journal,1971,11(3):306-314.
[3]HILL A D,LINDSAY D M,SILBERBERG I H,etal.Theoretical and experimental studies of sandstone acidizing[J].Old SPE Journal,1981,21(1):30-42.
[4]LABRID J.Thermodynamic and kinetic aspects of argillaceous sandstone acidizing[J].Old SPE Journal,1975,15(2):117-128.
[5]LUND K,FOGLER H S.Acidization—V:the prediction of the movement of acid and permeability fronts in sandstone[J].Chemical Engineering Science,1976,31(5):381-392.
[6]HEKIM Y,FOGLER H S.On the movement of multiple reaction zones in porous media[J].AIChE Journal,1980,26(3):403-411.
[7]TAHA R,HILL A D,SEPEHMOORI K.Simulation of Sandstone-Matrix Acidizing in Heterogeneous Reservoirs[J].Journal of Petroleum Technology,1986,38(7):753-767.
[8]BRYANT S L.An improved model of mud acid/sandstone chemistry[C].SPE Annual Technical Conference and Exhibition,1991.
[9]QUINN M A,LAKE L W,SCHECHTER R S.Designing effective sandstone acidizing treatments through geochemical modeling[J].Old Production &Facilities,2000,15(1):33-41.
[10]RAHMAN S.A 3-D Numerical model for designing and planning of matrix acid stimulation in low-permeability rocks[C].SPE Asia Pacific Oil and Gas Conference and Exhibition,2000.
[11]RODOPLU S,ZHU D,HILL A D,et al.Development and validation of a sandstone acidizing model with a new permeability response model[C].SPE Annual Technical Conference and Exhibition,2003.
[12]LI C,XIE T,POUMIK M,et al.Fine-scale simulation of sandstone acidizing[C].SPE Annual Technical Conference and Exhibition,2004.
[13]XIE T,LI C,POUMIK M,et al.A Laboratory and modeling investigation of acid-created wormholes in sandstones[C].SPE European Formation Damage Conference,2005.
[14]ZOU J,LI M,ZHAO L,et al.A new real-time monitoring method for sandstone reservoirs' acidizing[C].SPE Asia Pacific Oil &Gas Conference and Exhibition,2006.
[15]LI S Y,LI Z M,LI B F.Acid/sandstone reaction modeling for sandstone-matrix acidizing[J].Journal of China University of Mining &Technology,2012,2:13.
[16]陈钢,魏建军,王树军,等.砂岩油藏注水井深部酸化技术[J].石油钻采工艺,2007,29(3):45-48.
(修改稿收到日期 2013-12-18)
(编辑 景 暖)
Sandstone acidizing simulation based on exponential damage model
LIU Pingli1,XUE Heng1,LI Nianyin1,LUO Zhifeng1,XING Xijin2,SHAN Jincheng3
(1.State Key Laboratory of Oil &Gas Reservoir Geology and Exploitation Engineering,Southwest Petroleum University,Chengdu610500,China;2.CNOOC Research Institute,Beijing100027,China; 3.CNOOC China Ltd.,Tianjin300452,China)
A mathematical model of sandstone matrix acidizing radial heterogeneous flow reaction which conforms to reservoir scale,is developed based on Heterogeneous Sandstone Reservoir Generalized Distribution Model and Fine Scale Sandstone Acidizing Model.In order to study the effect of pore and permeability distribution differences of damage zone on acidification simulation,the permeability of damage zone was assumed as exponential distribution.By introducing the model of pore and permeability distribution differences of damage zone and exponential model into radial heterogeneous flow mathematical model respectively,we focused on the influence of different damage zone assumption on acidizing simulation effect.Simulation results show that in the former case the formation porosity along the radial direction is diminishing after acidizing,while in latter case the formation porosity along the radial direction is still increasing after acidizing and porosity undulates more gently along radial direction,indicating that seepage conditions is improved evenly in the damage zone and the result conforms to the real situation.Under the same condition of injection,acidification effect of exponential model calculation is more significant.Compared with the small injection rate,the large one is helpful to increase acid penetration distance,but both of the stimulation ratios are almost same.
Sandstone;matrix acidizing;acid-rock reaction;damage simulation; mathematical model; numerical simulation
刘平礼,薛衡,李年银,等.基于指数伤害模型的砂岩酸化模拟[J].石油钻采工艺,2014,36(1):79-84.
TE357.2
:A
1000-7393(2014)01-0079-06
10.13639/j.odpt.2014.01.021
国家科技重大专项“大型油气田及煤层气开发项目(2011ZX05030-005-08)”;示范工程项目(2011ZX05044)。
刘平礼,1973年生。1998年获西南石油大学油气田开发工程专业硕士学位,现主要从事采油工程教学和压裂酸化方向研究工作。电话:028-83032911。E-mail:liupingli@vip.163.com。

