基于SINS/GNSS的航空矢量重力测量数据处理方法研究

宁津生

（1.武汉大学测绘学院，武汉 430079；2.武汉大学地球空间环境与大地测量教育部重点实验室，武汉 430079）

基于SINS/GNSS的航空矢量重力测量数据处理方法研究

宁津生1，2

（1.武汉大学测绘学院，武汉 430079；2.武汉大学地球空间环境与大地测量教育部重点实验室，武汉 430079）

航空矢量重力测量是未来高效测定中高频地球重力场信息的先进技术，与地面重力测量、海洋重力测量和卫星重力测量技术相互补充。本文介绍了基于捷联惯性导航系统/全球卫星导航系统（SINS/ GNSS）的航空矢量重力测量的原理，重点讨论了航空矢量重力测量的数据预处理、数据归算、带限地形影响、向下延拓及大地水准面确定等问题，为发展我国航空矢量重力测量技术提供参考。

航空矢量重力测量；SINS/GNSS数据融合；地球重力场；大地水准面

1 前言

航空重力测量技术是以飞机为载体，快速测定近地空中重力加速度的重力测量方法。航空重力测量最早出现在20世纪50年代，经过数十年的沉淀与发展，已成为高效测定中高频地球重力场信息的主要手段。在地面重力测量难以到达的地区进行航空重力测量，可以有效填补困难地区的重力空白，有利于改善重力场数据的精度和分辨率及精化局部重力场模型和区域大地水准面。航空重力测量结合其他技术手段获取的高精度地球重力场信息，在国家经济建设、军事和国防建设、地球物理、海洋学、地球动力学、资源勘探等相关地球科学领域具有重要作用。

以美国、加拿大、丹麦等为代表的发达国家先后开展了航空重力测量研究，并进行了大量的飞行试验[1～3]，我国也在2002年成功研制了自己的航空标量测量系统Chinese airborne gravimetry system（CHAGS）[4]。众多研究结果表明，航空标量重力测量数据在波长5～10 km的尺度上能够达到1～3 mGal（1 Gal=0.01 m/s2）的精度，这也意味着航空标量重力测量技术已经进入成熟阶段。航空矢量重力测量技术不仅能获取航空标量重力测量观测值（即重力矢量的垂直分量），也能测得重力矢量的水平分量，是目前大地测量领域的研究热点之一。Jekeli和Garcia[5]验证了全球卫星导航系统（GNSS）相位加速度应用于航空矢量重力测量的可行性；Kwon和Jekeli[6，7]等率先启动关于航空矢量重力测量的研究与试验并提出了利用惯性导航系统（INS）/GNSS组合系统测定矢量重力的新方法，所得重力矢量垂直分量精度为3 mGal，水平分量精度为6～8 mGal，分辨率为10 km；Senobari[8]给出了基于捷联惯性导航系统（SINS）/GNSS的航空矢量重力测量的试验结果；美国政府也于2012年开始为期10年的GRAV-D计划，并将航空矢量重力测量作为其中的一项关键技术，预期确定北美地区大地水准面的精度达到2 cm[9]。目前国内还没有航空矢量重力测量系统，在航空矢量重力数据处理方面也尚处于起步阶段。因此，充分吸收国内外现有研究成果，深入研究航空矢量重力测量的基础理论和数据处理方法，对我国航空矢量重力测量技术的发展具有重要的科学意义和应用价值。

2 基本原理

依据牛顿第二定律，单位质点的加速度在数值上等于质点所受作用力的合力。在惯性系i系中质点的运动方程可写为

ai=fi+gi（1）

式（1）中，ai为惯性加速度，由GNSS观测值给出；fi为比力观测值，由SINS给出；gi为重力加速度。将重力加速度矢量表示为正常重力矢量γn与扰动重力δgn之和，则在导航坐标系n系中，航空矢量重力测量的基本模型可表示为

式（2）中，右边第三项为Coriolis加速度；Ωnie为地心地固坐标系e系相对于i系的旋转角速度；Ωnen为n系相对于e系的旋转角速度。对基于SINS/GNSS的航空矢量重力测量系统来说，加速度计和陀螺仪固定在载体上，比力是在载体坐标系b系中测得的，因此需要利用陀螺仪数据将比力转换至导航坐标系n系，此时式可写为

式（3）中，Rnb为b系到n系的旋转矩阵。

3 数据处理方法

3.1 数据预处理

航空矢量重力测量是一个动态测量过程，各类观测数据中均包含了大量的观测噪声，如何从低信噪比的加速度观测信息中有效地提取重力信息是航空矢量重力测量数据处理的关键。这一过程又大致可分为数据去噪、误差补偿、数据融合、低通滤波等，具体数据处理流程如图1所示。在数据预处理过程中对原始观测数据进行去噪和误差补偿，可以提高数据的信噪比，进而提高数据处理精度。惯性测量单元（inertial measurement unit，IMU）是航空矢量重力测量系统的重要组成部分，主要由加速度计和陀螺仪构成。由于IMU自身的误差特性，在外业测量前需对其进行外场标定，提高数据质量，减小系统误差对后续数据处理带来的影响[10]。

图1 航空矢量重力测量的数据预处理Fig.1 Data preprocessing of airborne vector gravimetry

初始对准是SINS在进行各种应用前所必需的一项重要工作，计算出b系与n系或者i系之间的姿态转移矩阵，其对准精度对后续的各种应用产生直接影响，而Kalman滤波技术是实现初始对准的一种有效方法。最优的Kalman滤波器是建立在函数模型和噪声特性均精确已知的条件下，但噪声统计特性一般难以获得，自适应Kalman滤波是解决这一应用难题的主要方法之一。根据IMU的自身特性以及作业场地等因素，加速度计的噪声特性通常是未知的，本文提出了基于简化自协方差最小二乘（autocovariance least-squares，ALS）噪声估计的SINS静基座初始对准算法（SALS），计算流程见图2。

图2 基于简化ALS噪声估计的SINS静基座初始对准流程图Fig.2 Flow chart of the simplified ALS for SINS initial alignment on stationary base

图3给出了数值仿真中东、北、天方向姿态角的初始对准误差，从中可以看出，天方向姿态角比水平方向姿态角更易受观测噪声协方差矩阵的影响，当先验观测噪声协方差矩阵存在较大偏差时，对天方向对准结果有较大影响；本文提出的基于简化ALS噪声估计的SINS SALS同时进行噪声估计和姿态角修正，因此各方向姿态角的对准精度较常规Kalman滤波方法有着明显得提高。静基座初始对准的Kalman滤波模型并非完全可观，三个失准角由于受陀螺常值漂移和加速度计常值漂移的影响，故均存在估计偏差。

图3 初始对准误差Fig.3 Errors of initial alignment

载体的运动加速度是最重要的改正项，其精度直接影响着航空重力测量的精度和空间分辨率[11，12]，但载体加速度并非直接观测值，它是通过载体位置或速度差分计算得到的。理论上，已知载体位置的时间序列，采用数值差分的方法便可得到载体加速度的时间序列，但由于数值差分过程会放大高频噪声，在实际数据处理中，还需进行低通滤波，然而当噪声和信号在同一频带上有交叠时，采用低通滤波方法必然会造成信号损失，且不同的低通滤波器及其参数的选择也会对信号处理结果有一定的影响。Kalman滤波方法是一种基于模型的数字滤波方法，可以用来确定载体的加速度。在进行航空重力测量时，一般要求飞行过程比较平稳，因此可采用常加速度模型对载体运动状态进行建模。由于Kalman滤波模型的噪声协方差矩阵特别是状态噪声协方差矩阵难以获取，不适当的噪声参数的选取必然会对Kalman滤波的结果带来影响。而顾及常加速度模型的状态噪声协方差矩阵满足特定结构[13]，本文提出了一种基于ALS噪声估计的载体加速度确定算法，其计算流程见图4。

图4 基于ALS噪声估计的载体加速度确定算法流程图Fig.4 Flow chart of the ALS method for acceleration estimation

表1中5种不同方案的状态估计结果表明：a.采用9点差分法计算得到的速度和加速度精度最差；b.当先验噪声协方差存在较大偏差时，Kalman滤波精度较差，再采用RTS算法进行平滑处理，其状态估计精度提高有限；c.先采用ALS进行噪声估计，再进行RTS平滑，其状态估计精度有着明显提高。图5说明差分法的差分误差在高频部分特别显著，采用ALS及RTS平滑算法不仅在高频段对误差有较好的抑制作用，在低频段对信号的拟合精度也明显优于差分法。

表1 加速度计算结果比较Table 1 Results comparison of acceleration

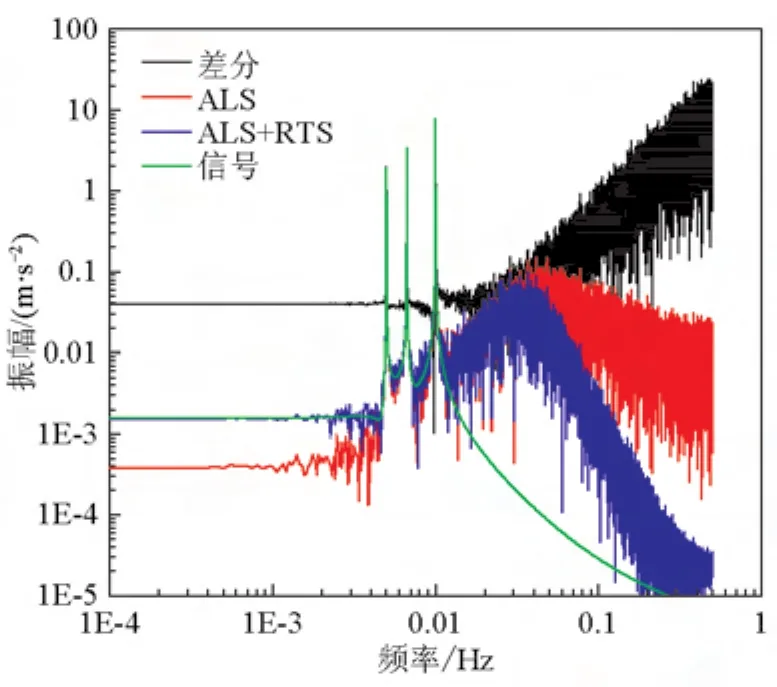
图5 加速度的频谱图Fig.5 Spectrum of acceleration

INS具有较高的短期稳定性，但误差随着时间累积，而GNSS具有较高的精度，但可能存在数据空白。基于两者的互补性，通过差分GNSS得到载体的运动加速度，将载体加速度与比力及正常重力的差值作为观测信息来建立Kalman滤波模型，并对SINS的各种误差进行估计，此时扰动重力矢量存在于Kalman滤波的观测残差中，从而可提取到测线上的扰动重力。Kalman滤波是SINS/GNSS数据融合时最为常用的数据处理方法，但其有效性有待在实际数据处理中得到验证。

数据融合后得到的测线扰动重力中仍含有大量的高频噪声，大量研究和试验表明，低通滤波技术是消除高频噪声的有效方法，国内外学者针对航空标量重力测量数据的低通滤波做了大量的研究[13～18]。本文采用窗函数法（滤波器1）和最佳一致逼近法（滤波器2）设计了适用于航空矢量重力测量数据处理的FIR数字低通滤波器，结合GPS静态测量数据进行了数值试验。结果如图6所示，说明两类滤波器均能以±1～2 mGal的精度确定垂直加速度，以高于±1 mGal的精度确定水平加速度。

图6 滤波后GPS测站的加速度Fig.6 Accelerations of GPS station after lowpass filtering

3.2 数据归算

为满足地球重力场有关研究及相关应用的需要，航空矢量重力观测值往往被归算成平均飞行高度面上规则格网化的扰动重力，这一过程包括平均高度面归算、测线网平差和格网化数据生成。平均高度面归算本质上可理解为实测数据相对于平均高度面的向上延拓或向下延拓改正，因此平均高度面归算可采用重力延拓方法，如谱方法[19]、泊松积分法[20]和径向改正方法[21]等，当实际航线相对于平均高度面的变化较小时，一般只考虑径向改正方法。测线网平差实际上是一个系统误差的补偿问题，进行系统误差补偿的一般方法为自检校平差法，但其设计矩阵是秩亏的，这时可选定某一条或几条精度很高的测线作为固定测线，将这些测线的系统误差作为虚拟观测值，按秩亏自由网平差法进行求解[22]。但在很多情况下，因观测区域的地面检校数据不足，观测数据的精度无法准确评定，此时可采用两步平差法来进行系统误差补偿[23～25]。航空重力测量数据归算的目的是获得平均飞行高度面上具有一定空间分辨率、按经纬度划分的规则格网重力数据，格网化方法的好坏对格网化输出数据的质量、精度和可信度有着直接影响。重力数据处理中常用的格网化方法主要有加权平均法、Shepard曲面拟合法、Kriging方法和最小二乘配置法（LSC），这些格网化方法有着各自的优缺点，在实际应用中有所差异。

3.3 带限地形影响

地形起伏反映了地球重力场的不规则变化，精确确定地形对地球重力场的影响具有十分重要的意义[26]。第二类Helmert凝集法是目前应用最为广泛的地形归算方法，分为解析形式和谱形式，前者提供全波段的地形质量改正，后者则是将牛顿积分核函数展开成Legendre多项式的收敛级数，可用来计算带限地形影响。

航空重力测量的各类观测数据中包含了大量的高频观测噪声，消除这些噪声的主要手段是使用低通滤波器，滤波后得到的重力信号为带限重力信号[27]。因此，采用解析公式计算的全频谱地形直接影响和间接影响对航空矢量重力观测值进行改正是不合理的，解决这一问题的方法有两类：a.将地形改正值也作相应的低通滤波处理，使得地形效应的频谱范围与航空重力观测值一致[28]，这种方法需要输入飞行高度上密集采样点处的地形质量影响值，采用高分辨率的数字高程模型（digital elevation model，DEM）来进行计算时工作量相当庞大；b.基于第二类Helmert凝集法的谱形式，采用带限公式来计算地形质量对引力位和重力扰动的直接影响公式和大地水准面的间接影响[29]。这种方法的优点是可依据重力观测值的频谱范围来调整积分核函数的起始阶数和最高阶数，从而避免了对地形质量影响作低通滤波处理，原理简单而且计算方便。Novák等[29]基于第二类Helmert凝集法的谱形式推导了地形质量对引力位和重力扰动的带限直接影响改正公式以及对大地水准面的带限间接影响改正公式，将基于级数核计算的带限直接地形影响和间接地形影响与基于解析核计算并经低通滤波处理后得到的带限直接地形影响和间接地形影响进行了比较，验证了算法的有效性，该带限地形影响改正公式可对重力扰动或重力异常进行地形归算，针对的是航空标量重力测量观测值。航空重力矢量测量获取的是扰动重力的三个分量，而针对水平分量带限地形影响改正的研究尚未有公开的文献发表。本文在Novák研究的基础上，推导了重力矢量水平分量的带限直接地形影响改正公式，并在中国西部山区选取了两条沿纬圈方向4 000 m（大地高）航线高度上的航线，采用3″×3″的数字高程模型基于解析核计算了水平分量的直接地形影响，经低通滤波后与基于带限公式计算的地形影响进行了比较。数值计算结果如图7～图10所示，表明二者吻合较好。

3.4 向下延拓

航空矢量重力测量的观测值为近地空中的中高频重力信号，但地球物理和大地测量领域的许多应用都需要地形表面或大地水准面上的重力观测值。因此，将航线上的重力测量观测值进行向下延拓，是航空矢量重力测量数据处理的主要内容之一。

向下延拓是一个不适定的过程，属于病态问题，会放大重力观测数据中的噪声，若不采用合适的延拓方法，将会导致延拓解的严重失真。在现有的向下延拓方法中，逆Possion积分法的应用最为广泛，逆Possion积分法辅以Tikhonov正则化[20]、岭估计[30]、广义岭估计[30]、迭代法[31]、滤波[32，33]等正则化方法才能得到稳定的延拓解，其关键在于选择合理的正则化参数。Novák和Heck[34]认为航空重力为带限信号，提出了基于带限Possion核函数的直接延拓法，从而避免了逆Possion积分法面临的大型法方程阵求逆问题。LSC兼具向上延拓和向下延拓的双重功能，在延拓过程中可融入新的重力数据且能有效估计和改善系统偏差[32]，但LSC延拓结果的好坏很大程度上取决于协方差函数模型。解析延拓也是重力信号向下延拓的一种常用方法，同样兼具向上延拓和向下延拓的能力，其基本思想是假设重力信号的垂直梯度已知，则延拓表达式可表示为一个Taylor展开级数；解析延拓在空域中的求解十分复杂，Wu[35]给出了解析延拓在频域中的求解公式。此外，一些数学方法如样条函数法、小波算法等的引入，使得重力信号向下延拓的手段更加丰富。

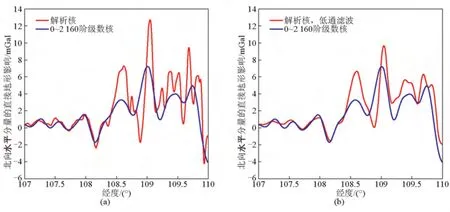
图7 沿31.5°N纬线4 km飞行高度处北向水平分量的直接地形影响Fig.7 Direct topographical effect for northern component at 4 km flight height along the parallel of 31.5°N

图8 沿32.5°N纬线4 km飞行高度处北向水平分量的直接地形影响Fig.8 Direct topographical effect for northern component at 4 km flight height along the parallel of 32.5°N

图9 沿31.5°N纬线4 km飞行高度处东向水平分量的直接地形影响Fig.9 Direct topographical effect for eastern component at 4 km flight height along the parallel of 31.5°N

以上方法一般用于航空标量重力测量数据，即重力扰动（重力异常）的向下延拓，而航空矢量重力测量不仅能获取重力扰动（重力矢量的垂直分量），还能测出重力矢量的水平分量。理论上水平分量的向下延拓原理与垂直分量类似，但现有公开发表的文献中针对水平分量向下延拓的研究较少，且由于航空矢量重力测量技术自身的缺陷，空中获取的水平分量的精度远不如垂直分量，仅为6～8 mGal，如何实现低信噪比情况下水平分量的向下延拓是一个需要解决的关键问题。本文引入了频域输入输出系统，在不同的噪声水平下比较分析了单输入单输出系统（single-input single-output system，SISOS）和双输入单输出系统（double-input singleoutput system，DISOS）对水平分量的向下延拓效果（见图11和图12）。研究结果表明：a.当水平分量的精度较高（如1.5 mGal）时，二者均能实现水平分量的稳定向下延拓；b.当水平分量的精度较低（如6 mGal）时，单输入单输出法的延拓结果较差，而双输入单输出法能实现水平分量的稳定向下延拓。

图10 沿32.5°N纬线4 km飞行高度处东向水平分量的直接地形影响Fig.10 Direct topographical effect for eastern component at 4 km flight height along the parallel of 32.5°N

图11 东向分量的精度为1.5 mGal时延拓误差的空间分布Fig.11 Distribution of continued errors of estern component with the accuracy of 1.5 mGal

图12 东向分量的精度为6 mGal时延拓误差的空间分布Fig.12 Distribution of continued errors of estern component with the accuracy of 6 mGal

4 航空矢量重力应用于大地水准面的确定

利用航空矢量重力测量数据确定大地水准面可归结为求解航空矢量重力测量边值问题。与传统的重力学边值问题不同，航空矢量重力测量边值问题的边界面为飞行高度面，可描述为[36]

式（4）中，Δ为拉普拉斯算子；T为扰动位；H为航线高度。由式（4）可知，扰动重力的水平分量和垂直分量均可用于精化区域大地水准面。垂直分量在全波长为5～10 km的分辨率尺度上能达到1～3 mGal的精度，已能满足区域大地水准面确定的要求。

利用垂直分量确定大地水准面的方法主要有两类。第一类为空域积分法，它可分为两步法和一步法[37]。两步法包括两个计算步骤：a.求解位理论Dirichlet边值问题，将飞行高度面上的垂直分量向下调和延拓至大地水准面；b.求解位理论Neumann边值问题，按照Hotine积分公式由大地水准面上的垂直分量得到大地水准面上的扰动位，再由Bruns公式得到大地水准面高。一步法是一种比两步法更稳定、精度更高的空域解法，它将向下延拓和求解大地水准面进行了综合。由于航空重力观测值为带限信号，一步法采用频谱范围与观测值一致的带限积分核函数，由广义Hotine积分公式结合Bruns公式即可得到大地水准面高。第二类为谱方法。通过某种形式的逼近，Hotine积分、Possion积分可化为空域卷积形式。研究表明，采用快速傅里叶变换（fast Fourier transform，FFT）将Hotine积分和Possion积分转换至频域进行计算可使积分法的计算速度得到极大的提升[38～40]。此外，还可采用球冠谐分析或矩谐分析将重力观测数据表达为局域重力场的谐展开式。球冠谐分析[41]和矩谐分析[42]最早应用于地磁场表达，Li等[43]首次将球冠谐分析引入区域重力场研究中，边少峰[44]和蒋涛[30]则将矩谐分析用于局部重力场表达。对于大范围的区域重力场逼近，球冠谐分析是一种较为理想的方法，而矩谐分析则适用于区域重力场精细结构的逼近。

类似于天文水准原理，可采用逐测线剖面积分将扰动重力的水平分量转化为航线上的扰动位，将扰动位向下延拓至大地水准面后，再采用Bruns公式计算大地水准面起伏[45]。值得注意的是，垂直分量确定的是绝对大地水准面，而水平分量确定的是相对大地水准面。

在联合重力矢量的三个分量精化大地水准面方面，随机解法、频域输入输出法、多分辨率配置法、谱组合法等方法可将航线的重力矢量转化为航线上的扰动位，将扰动位向下延拓至大地水准面，再采用Bruns公式计算大地水准面起伏。目前航空矢量重力测量水平分量的精度水平远不如垂直分量，需要分析不同信噪比情况下的水平分量对三分量联合求解大地水准面的影响，进一步研究联合航空重力矢量的三个分量确定大地水准面的融合方法。

5 结语

基于SINS/GNSS的航空矢量重力测量是未来高效测定中高频地球重力场信息的先进技术，联合地面重力测量、海洋重力测量和卫星重力测量技术，可以获取全球高分辨率高精度地球重力场信息，从而满足国家经济建设、军事和国防建设、地球物理、海洋学、地球动力学、资源勘探等相关地球科学领域的需求。本文在国内外现有研究成果的基础上，讨论了航空矢量重力测量的数据预处理、数据归算、带限地形影响、向下延拓及大地水准面确定等问题。

航空矢量重力测量技术的实用化还需要解决一系列关键问题，如高精度SINS的自主研制、SINS/ GNSS的数据融合方法及满足工程化应用的数据处理软件、SINS和GNSS的误差校正、地壳横向密度扰动对向下延拓和精化大地水准面的影响、航空矢量重力及其他类型重力场信息的融合处理等。

[1]Wei M，Schwarz K P.Flight test results from a strapdown airborne gravity system[J].Journal of Geodesy，1998，72：323-332.

[2]Verdun J，Klingelé E，Bayer R，et al.The alpine Swiss-French airborne gravity survey[J].Geophysical Journal International，2003，152：8-19.

[3]Forsberg R，Olesen A，Vest A，et al.Gravity field improvements in the north atlantic region[C]//Proc.GOCE Workshop，ESA-ESRIN，2004.

[4]夏哲仁，石 磐，孙中苗，等.航空重力测量系统CHAGS[J].测绘学报，2004，33（3）：216-220.

[5]Jekeli C，Garcia R.GNSS phase accelerations for movingbase vector gravimetry[J].Journal of Geodesy，1997，71：630-639.

[6]Kwon J.Airborne vector gravimetry using GNSS/INS[D].USA：The Ohio State University，2000.

[7]Kwon J，Jekeli C.A new approach for airborne vector gravimetry using GNSS/INS[J].Journal of Geodesy，2001，74（10）：690-700.

[8]Senobari M S.New results in airborne vector gravimetry using strapdown INS/GNSS[J].J Geoid，2010，84：277-291.

[9]Smith D.The GRAV-D project：Gravity for the redefinition of the American Vertical Datum[OL].NOAA website：http：//www. ngs.noaa.gov/GRAV-D/pubs/GRAV-D_v2007_12_19.pdf，2007.

[10]Lee J G，Park C G，Park H W.Multiposition alignment of strapdown inertial navigation system[J].Aerospace and Electronic Systems，IEEE Transactions on，1993，29（4）：1323-1328.

[11]Kwon J H，Jekeli C.A new approach for airborne vector gravimetry using GNSS/INS[J].Journal of Geodesy，2001，74（10）：690-700.

[12]孙中苗.航空重力测量理论，方法及应用研究[D].郑州：解放军信息工程大学，2004.

[13]Singer R A.Estimating optimal tracking filter performance for manned maneuvering targets[J].IEEE Transactions on Aerospace and Electronic Systems，1970（4）：473-483.

[14]Hammada Y.A comparison of filtering techniques for airborne gravimetry[D].Calgary：Department of Geomatics Engineering at University of Calgary，1996.

[15]孙中苗.航空重力测量中FIR低通滤波器的设计与应用[J].解放军测绘学院学报，1996，13（4）：247-250.

[16]柳林涛，许厚泽.航空重力测量数据的小波滤波处理[J].地球物理学报，2004，47（3）：490-494.

[17]孙中苗，翟振和.航空重力测量数据的小波阈值滤波[J].武汉大学学报（信息科学版），2009，34（10）：1222-1225.

[18]蔡劭琨，吴美平，张开东.航空重力测量中FIR低通滤波器的比较[J].物探与化探，2010，34（1）：74-78.

[19]蒋 涛，党亚明，章传银，等.基于矩谐分析的航空重力向下延拓[J].测绘学报，2013，42（4）：475-480.

[20]王兴涛，石 磐，朱非洲.航空重力测量数据向下延拓的正则化算法及其谱分解[J].测绘学报，2004，33（1）：33-38.

[21]钟 波，刘华亮，罗志才，等.卫星重力梯度数据的归算与格网化处理[J].大地测量与地球动力学，2011，31（3）：79-84.

[22]Hwang C，Hsiao Y S，Shih H C.Data reduction in scalar airborne gravimetry：Theory，software and case study in Taiwan [J].Computers&Geosciences，2006，32（10）：1573-1584.

[23]黄谟涛，翟国君，欧阳永忠，等.海洋重力测量误差补偿两步处理法[J].武汉大学学报（信息科学版），2002，27（3）：251-255.

[24]周波阳，罗志才，林 旭，等.航空重力测量测线网平差中的粗差处理[J].大地测量与地球动力学，2012，32（2）：110-114.

[25]周波阳，罗志才，林 旭.航空重力测量测线网平差中的粗差处理方法[C]//中国地球物理学会第二十七届年会论文集.合肥：中国科技大学出版社，2011.

[26]罗志才，宁津生，晁定波.卫星重力梯度向下延拓的谱方法[J].测绘学报，1997，26（2）：168-175.

[27]Novák P，Kern M，Schwarz K P.Numerical studies on the harmonic downward continuation of band-limited airborne gravity [J].Studia Geophysica et Geodaetica，2001，45（4）：327-345.

[28]Bayoud F A，Sideris M G.Two different methodologies for geoid determination from ground and airborne gravity data[J]. Geophysical Journal International，2003，155（3）：914-922.

[29]Novák P，Kern M，Schwarz K P，et al.Evaluation of band-limited topographical effects in airborne gravimetry[J].Journal of Geodesy，2003，76（11-12）：597-604.

[30]蒋 涛.利用航空重力测量数据确定区域大地水准面[D].武汉：武汉大学，2011.

[31]Serpas J.Local and regional geoid determination from airborne vector gravimetry[D].USA：The Ohio State University，2003.

[32]Hwang C，Hsiao Y S，Shih H C，et al.Geodetic and geophysical results from a Taiwan airborne gravity survey：Data reduction and accuracy assessment[J].Journal of Geophysical Research：Solid Earth（1978-2012），2007，112（B4）.

[33]周波阳，罗志才，许 闯，等.航空重力测量数据向下延拓最小二乘配置法和逆Possion积分法的比较[C]//中国地球物理.合肥：中国科技大学出版社，2012.

[34]Novák P，Heck B.Downward continuation and geoid determination based on band-limited airborne gravity data[J].Journal of Geodesy，2002，76（5）：269-278.

[35]Wu L.Spectral methods for post processing of airborne vector gravity data[D].Canada：University of Calgary，1996.

[36]Schwarz K P，Li Z.An introduction to airborne gravimetry and its boundary value problems[M]//Geodetic boundary value problems in view of the one centimeter geoid.Germany：SpringerBerlin Heidelberg，1997：312-358.

[37]Novák P.Optional model for geoid determination from airborne gravity[J].Studia geophysica et geodaetica，2003，47：1-36.

[38]Schwarz K P，Sideris M G，Forsberg R.The use of FFT techniques in physical geodesy[J].Geophysical Journal International，1990，100（3）：485-514.

[39]Sideris M G，She B B.A new，high-resolution geoid for Canada and part of the US by the 1D-FFT method[J].Bulletin Géodésique，1995，69（2）：92-108.

[40]周波阳，罗志才，林 旭，等.航空重力数据向下延拓FFT快速算法比较[J].大地测量与地球动力学，2013，33（1）：64-68.

[41]Haines G V.Spherical cap harmonic analysis[J].Journal of Geophysical Research：Solid Earth（1978-2012），1985，90（B3）：2583-2591.

[42]Alldredge L R.Rectangular harmonic analysis applied to the geomagnetic field[J].Journal of Geophysical Research，1981，86（B4）：3021-3026.

[43]Li J C，Chao D B，Ning J S.Spherical cap harmonic expansion for local gravity field representation[J].Manuscripta Geodaetica，1995，20：265-277.

[44]边少峰.大地测量边值问题数值解法与地球重力场逼近[D].武汉：武汉测绘科技大学，1992.

[45]Jekeli C，Kwon J H.Geoid profile determination by direct integration of GNSS inertial navigation system vector gravimetry[J].Journal of Geophysical Research：Solid Earth（1978-2012），2002，107（B10）：ETG 3-1-ETG 3-10.

Research on the data processing methods of airborne vector gravimetry using SINS/GNSS

Ning Jinsheng1，2
（1.School of Geodesy and Geomatics，Wuhan University，Wuhan 430079，China；2.Key Laboratory of Geospace Environment and Geodesy，Ministry of Education，Wuhan University，Wuhan 430079，China）

Airborne vector gravimetry is an advanced and efficient technology to determine high frequency information of earth’s gravity field in the future，and is a complement to ground gravimetry，marine gravimetry and satellite gravimetry.The principle of airborne vector gravimetry using SINS（strapdown inertial navigation system）/GNSS（global navigation satellite systems）is introduced in the paper，and then the data preprocessing，data reduction，band-limited topographical effect and downward continuation are discussed，as well as the geoid determination from airborne vector gravimetry.It provides the support for the development of airborne vector gravimetry in our country.

airborne vector gravimetry；SINS/GNSS data fusion；earth gravity field；geoid

P227

A

1009-1742（2014）03-0004-10

2013-12-03

国家自然科学基金项目（41174062）；地球空间环境与大地测量教育部重点实验室开放基金项目（12-02-05，12-02-09）

宁津生，1932年出生，安徽桐城县人，中国工程院院士，教授，主要从事物理大地测量的教学和科研工作；E-mail：jsning@sgg.whu.edu.cn