基于SEM方法的多层次大型综合性医院患者满意度指数模型研究

中南大学公共管理学院（410083） 刘芷含

基于SEM方法的多层次大型综合性医院患者满意度指数模型研究

中南大学公共管理学院（410083） 刘芷含

目的对于大型综合性医院而言，患者满意度测评是评价医院服务质量，改进医院工作的重要内容之一。国内在患者满意度综合测评中所采用的一些传统的多因素分析方法有待改进。方法在全国五个地区各选一家在国内很有影响和代表意义的大型综合性医院开展抽样调查，采用多层线性模型与结构方程模型相结合的方法。结果构建了多层次的大型综合性医院患者满意度指数模型，并通过实证分析证实其与实际数据契合，可合理地估计单个观测变量对满意度的影响，而且可以在不同层面上进行不同医疗服务领域间患者满意度的比较。结论本模型可为国内患者满意度指数模型的类似研究作参考。

大型综合性医院 患者满意度 指数模型 结构方程 SEM方法

对于大型综合性医院而言，患者满意度综合测评是评价医院服务质量，改进医院工作的重要内容之一［1］。国内在患者满意度综合测评中所采用的一些传统的多因素分析方法均有共同的缺陷，如没有考虑变量的测量误差、心理学变量之间的关系设定得比较简单等等，因而这些传统的多因素分析方法受到限制［2］。20世纪60年代末瑞典的Jreskog等学者在传统的探索性因子分析的基础上，将验证性因子分析、路径分析、多元回归分析等多种统计方法综合运用而发展出一种新的多因素分析方法即结构方程模型（structural equationmodeling，SEM）分析方法［3］。SEM不仅考虑了测量误差，而且可以反映变量间的复杂关系、完善了变量结构；不仅可以进行患者满意度指数的计算，而且可以进行患者满意度指数模型的构建。

本文通过在全国华北、华中、华东、华南和西南五个地区各选一家在国内很有影响和代表意义的大型综合性医院开展抽样调查，采用多层线性模型与结构方程模型相结合的方法，构建了多层次的大型综合性医院患者满意度指数（large comprehensive hospital patient satisfaction index，LCHPSI）模型，不但可合理地估计单个观测变量对满意度的影响，而且可以在不同层面上进行不同医疗服务领域间患者满意度的比较，较目前通常的单层次患者满意度指数模型有所创新。

测量模型和结构模型

结构方程模型主要是一种验证性因子分析（confirmatory factor analysis，CFA）技术，其本质是一个因果模型，包含了两类子模型：测量模型和结构模型。

1.测量模型

测量模型是以CFA方法来确定和评估观测变量和潜变量之间关系的一种模型，称为外部模型，用以下回归方程的矩阵形式表示

其中，X为外生潜变量ξ的观测值，其测量误差记作δ，Λx是观测变量X在外生潜变量ξ上的因子载荷矩阵Λx；Y是内生潜变量η的观测值，其测量误差记作ε，Λy是观测变量Y在内生潜变量η上的因子载荷矩阵［4］。

2.结构模型

结构模型是反映潜变量之间因果关系的一种模型，称为内部模型。结构模型用以下回归方程的矩阵形式表示。

其中，ζ是内生潜变量的残差，B是反映内生潜变量η之间联系的回归系数矩阵；Γ是反映外生潜变量ξ对内生潜变量η作用的回归系数矩阵记作Γ［4］。

3.结构方程模型的协方差结构

在结构方程中，由观测变量的总体可构造一个总体协方差矩阵∑，它反映了观测变量在总体中的真实关系。另外，根据研究所作出的模型假设，可得由式（1）～（3）组成的方程组，其模型参数组成向量θ。记∑（θ）为假设模型隐含的总体协方差矩阵，即理论预测的协方差矩阵。如提出的假设成立，则必有

对模型参数构成的向量θ进行统计学估计，设其估计值为，将其代入∑（θ），则所得的称为再生协方差矩阵。为证明所假设的模型是正确的，需通过一些实测样本去验证。设样本的协方差矩阵为S，则S是∑的估计，而∑是∑（θ）的估计。显然，在大样本和假设模型正确的情况下，矩阵应当收敛于∑-∑（θ），因而可据此评价假设模型与真实模型的接近程度［5］。

为将观测变量总体的协方差矩阵表示为以上结构方程模型结构参数的函数矩阵∑（θ），将∑（θ）写成分块矩阵形式

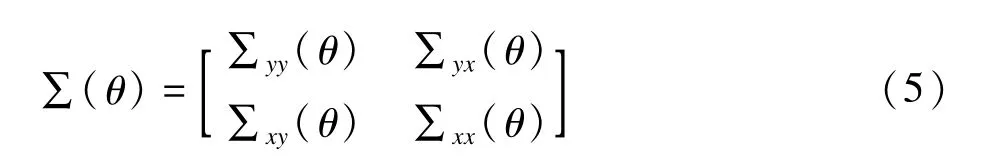
其中，∑yy（θ）为显变量向量y的协方差矩阵；∑yx（θ）为显变量向量y与x的协方差矩阵；∑xy（θ）为显变量向量x与y的协方差矩阵；∑xx（θ）为显变量向量x的协方差矩阵。注意到式（1）～（3），可求出各矩阵块

实证分析

1.LCHPSI模型的潜变量与显变量

本文创建的多层次大型综合性医院患者满意度指数模型，共涉及医院形象（Q1）、质量期望（Q2）、质量感知（Q3）、价值感知（Q4）、患者满意（Q5）和患者忠诚（Q6）等6个潜变量。Q1下设社会口碑（Q11）、专科特色（Q12）和治疗优势（Q13）等3个观测变量；Q2下设技术水平（Q21）、管理水平（Q22）和总体期望（Q23）等3个观测变量；Q3的观测变量分属医疗环境（Q31）、辅助服务（Q32）和医疗服务（Q33）等3个类别组，Q31组下设候诊秩序（Q311）、设施标志（Q312）和后勤保洁（Q313）等3个二级指标观测变量，Q32组下设挂号（Q321）、导诊咨询（Q322）、划价收费（Q323）和取药（Q324）等4个观测变量，Q33组下设等候时间（Q331）、医护态度（Q332）、指导用药（Q333）、辅助检查（Q334）、门诊治疗（Q335）和病症改善（Q336）等6个观测变量；Q4下设价格合理（Q41）1个观测变量；患者满意（Q5）下设医院比较（Q51）、总体满意（Q52）等2个观测变量；Q6下设再次就诊（Q61）和推荐亲友（Q62）等2个观测变量。

2.研究取样

本研究在全国华北、华中、华东、华南和西南五个地区各选一家在国内很有影响和代表意义的大型综合性医院，采用LCHPSI模型调查量表进行门诊患者满意度测评，共取得有效问卷表501份。

3.数据检验

为避免进行SEM分析时出现无法进行计算分析或虽进行了计算但所得的结果无法进行解释的现象，在进行SEM分析前需对样本数据进行检验，一般有多重共线性检验和正态性检验［6-7］。

4.患者满意度指数（LCHPSI）结构方程模型

（1）LCHPSI模型的标准化路径系数

采用AMOS19.0对本文创建的患者满意度指数（LCHPSI）模型进行SEM分析，得到LCHPSI模型的标准化路径系数图（图1）。

图1 LCHPSI模型的标准化路径系数图

（2）模型拟合指标检验

通过模型的拟合估计，得到的拟合效果指标如表1所示。

表1 模型的主要拟合效果指标值

从表1可以看出，卡方自由度比CMIN/DF为2.128，小于3的建议值，属良好适配；渐进残差均方根RMSEA为0.047，小于0.05的建议值；拟合优度指数GFI、调整的拟合优度指数AGFI、规范拟合指数NFI、增值拟合指数IFI、非规范拟合指数TLI以及比较拟合指数CFI的值均大于0.9的建议值［4］。模型中所有回归系数均具有统计显著性，通过显著性检验。说明本文构建的患者满意度指数（LCHPSI）模型合理，可以接受。

（3）模型分析

①结构模型分析

在结构模型中，反映了潜变量之间的关系。根据图1可得如下的关系式

从式（17）可以看出，患者满意受质量期望、质量感知、价值感知和医院形象的影响，其中影响最大的是质量感知，其次是价值感知，最后才是医院形象。这与人们对医院服务感受最强的信息来自医院的医疗质量的实际情况是一致的，说明医院应将质量放于一切工作的首位。本模型的研究验证了霍映宝博士的观点：感知质量显著性地决定顾客满意［9］。

从图1可以看出，模型中Q2对Q3和Q4有直接正向作用，即期望直接对质量感知和价值感知产生正向影响，这与ACSI模型一致。同时，本模型的研究验证了Fornell的观点：顾客期望对感知质量和感知价值有直接作用［10］

图1中Q2到Q3的路径系数为负，这与Oliver（1980）提出的期望-不一致”理论［11］是一致的，即患者通过医疗服务将实际表现给自己的感知与最初的期望相比较，当实际表现高于最初的期望时，患者就会感到满意，当实际表现低于原来的期望时，患者就会对医疗服务产生不满。本文的结果支持了期望-不一致理论。

从式（18）可以看出，Q1到Q6的路径系数为0.053，说明了医院形象对患者忠诚确有影响，但影响甚微。这是对品牌形象影响顾客忠诚学术观点的实证支持。式（18）还说明，在影响患者忠诚的两个潜变量医院形象和患者满意中，患者满意的影响力远大于医院形象。说明要使患者再次来就诊以及向亲友推荐，应努力提高患者满意度。

式（16）表明，价值感知受质量期望和质量感知的影响，但两者中受质量感知的影响较大。说明患者对价值的感受尽管受意识中一种预期的质量准则的影响，但更重要的是受患者在医疗过程中一种实际的服务质量体验的影响。

式（20）～（22）表明，在影响质量感知的三个中间潜变量医疗环境、辅助服务和医疗服务中，与患者最为关心的挂号、划价收费有关的中间潜变量辅助服务影响最大，其次是与患者最为看重的化验检查、门诊治疗有关的中间潜变量医疗服务。数据分析的结果与实际情况完全一致，说明通过多层次的模型构造和分析，可明确地反映不同的服务领域对患者质量感受的影响程度。

图1中其他潜变量的路径系数均为正，说明本文在建模时界定潜变量的基本思想理念是正确的。

②测量模型分析

根据图1可得外部测量模型和内部测量模型的回归系数如下：

从式（23）～（27）可以看出：

式（23）中，外生潜变量医院形象受观测变量治疗优势的影响较大，这正是大型综合性医院的优势之所在。

式（24）表明，潜变量质量期望受观测变量总体期望的影响最大，这和预期的一样，因为质量期望是总体期望的一个重要组成部分。其次是管理水平的影响较大，说明在患者心目中，除看重大型综合性医院的技术水平之外还相当看重这类医院的管理，认为去这类大型综合性医院就诊可靠，这也是为什么患者往往宁愿舍近求远去大型综合性医院就诊的原因之一。

式（25）表明，潜变量质量感知受观测变量化验检查、影像检查和划价收费影响最大，其次是后勤保洁和设施标志。说明患者对医疗服务质量的最直接的感受是在就诊过程中所做的各种检查的质量和收费情况，此外还受整个就诊环境优劣的影响。

式（26）表明，在测量潜变量患者满意的两个观测变量中，总体满意的影响要大于医院比较，这是符合人的思维习惯的。因为往往只有在不满意的情况下，人们才将此次就诊医院与以往体验过或听说过的其他医院进行比较，认为自己选择医院不当，并为以后不再来这家医院就诊埋设下了思想上的印记。

式（27）表明，观测变量再次就诊与推荐亲友对患者忠诚的回归系数大小基本相同，说明如果患者是医院的一名忠诚顾客，则除了自己会再次就诊外，还会向亲友力荐；反之，除自己断然不会再次就诊外，还一定会向亲友负面宣传。

从图1可以看出，各观测变量与其潜变量之间的标准化回归系数均在0.5至0.95之间，潜变量之间的标准化路径系数均没超过1，符合Bagozzi和Yi（1988）提出的参数估计值检验的原则［12］。综合以上数据检验及理性分析，说明本文构建的大型综合性医院患者满意度（LCHPSI）模型潜变量与观测变量之间的因果关系设置正确，测量指标设置得当，从不同侧面描述了患者在就诊过程中的体验和心理上的意愿，能较好地进行大型综合性医院患者满意度的评估。

结 语

通过对患者满意度指数（LCHPSI）模型的实证分析，证实了本文采用结构方程模型分析方法构建的大型综合性医院患者满意度指数（LCHPSI）模型潜变量与观测变量之间的因果关系设置正确，模型与实际数据契合；不但可合理地估计单个观测变量对满意度的影响，而且可以在不同层面上进行不同医疗服务领域间患者满意度的比较，可为国内患者满意度指数模型的类似研究所参考。

1.刘莎，许树强，田巍.基于排序求因子权重的门诊病人满意度多层次模糊综合评判研究.中国卫生统计，2011，28（4）：369-371.

2.刘莎，许树强，陈校云.基于灰色关联分析求因子权重的门诊病人满意度多层次模糊综合评判研究.中国卫生统计，2012，29（1）：37-39.

3.饶克勤主编.卫生统计方法与应用进展.北京：人民卫生出版社，2008.

4.吴明隆.问卷统计分析实务.重庆：重庆大学出版社，2011.

5.柯惠新，沈浩.调查研究中的统计分析方法.北京：中国传媒大学出版社，2005.

6.刘国旗.多重共线性的产生原因及其诊断处理.合肥工业大学学报，2001，24（4）：607-610.

7.Bowman K0，Shenton LR.Omnibus Contours for Departures from Normality Based onBiometrika，1975（58）：243-250.

8.Kline RB.Principles and Practice of Structural Equation Modeling，New York：The Guilford Press，1998：9.

9.霍映宝.顾客满意度测评理论与应用研究.南京：东南大学出版社，2010.

10.Fornell C，Johnson MD，Anderson EW，et al.The American Customer Satisfaction Index：Nature，Purpose and Findings.Journal of Marketing，1996，60：7-18.

11.Oliver RL.A Cognitive Model of the Antecedents and Consequences of Satisfaction Decisions.Journal of Marketing Research，1980，17（9）：460-469.

12.Bagozzi RP，Yi Y.On the Evaluation of Structural Equation Models. Academ ic of Marketing Science，1988，16：76-94.

（责任编辑：郭海强）