磁场和LO声子效应对量子盘中强耦合磁极化子qubit的影响

乌云其木格，白旭芳

(内蒙古民族大学物理与电子信息学院，内蒙古通辽，028043)

近年来，人们提出了多种实现量子比特的方案，如离子阱［1］、核与电子自旋［2，3］、量子点［4］等等，其中量子点量子计算机方案由于其具有能级结构可调，可以实现全光操作，便于实现量子比特的集成等优点，有可能作为量子光学技术的基本单元，因此许多学者对这样量子点量子比特进行了研究，获得了一系列重要结果。Jordan等［5］研究了固定Zeeman能量的单自旋量子比特的一致转动，Furuta等［6］研究了声表面波量子计算机的单量子比特门及测量，Li等［7，8］提出了利用外加电场来增加量子点量子比特消相干时间的方案。另外，由于大多数人工低维结构是离子晶体或极性材料制备的，而且因维度的降低，使得低维结构中电子-声子相互作用变得更加重要。事实上，电子-声子相互作用在决定低维系统一些物理性质，如输运性质、光学性质方面起着重要的作用［9，10］。因此，近年来许多学者对量子点中电子与声子相互作用对量子比特的影响进行了研究。Wu等［11］研究了与声子耦合双量子点中电荷量子比特动力学，Li等［12］采用Pekar型变分法研究了抛物量子点量子比特性质的磁场效应。Yu等［13］和Sun等［14］分别采用Pekar型变分法研究了单电子量子点量子比特。然而，不难看出，近年来人们对量子点中电子与声子相互作用对量子比特的影响的理论研究中，大多都为了简单起见把量子点当作理想的球形来处理。实际上，量子点的形状与生长条件有关，把量子点描述成其他形状如柱形或薄盘也许更为准确［15～17］。近年来，实验上已能作出几个分子层厚度的准二维量子点［18］。显然，对于约束在量子点内电子-声子相互作用体系而言，当厚度不为零时，将导致体统基态和激发态形式的变化。因此，面对量子点存在厚度的客观事实，研究量子点内电子-声子相互作用体系的性质随厚度的变化是有实际意义的基本问题。笔者采用Lee-Low-Pines-Huybrechts变分方法研究了外磁场、体纵光学(longitudinal optical，LO)声子效应和量子点厚度对量子盘中电子-LO声子强耦合磁极化子的振动频率和qubit的影响。

1 理论模型与方法

假定电子被限制在厚度为L的无限高势垒量子盘内，并与晶体中的体纵光学(LO)声子场相互作用。建立直角坐标系，Oz轴在盘的中心轴线上，x-y平面与盘中心轴线垂并通过盘的中点(图1)。设外磁场沿z轴方向，矢势用=B(－y，x，0)/2描写，则电子-LO声子相互作用体系的哈密顿量为

(1)式中第一项

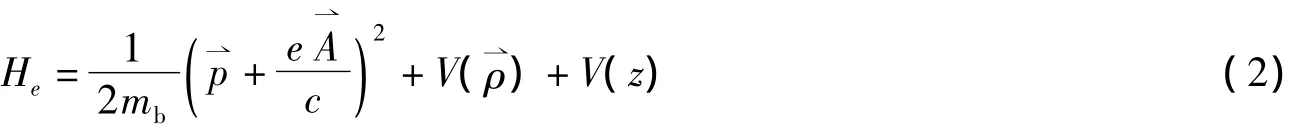
为电子的能量。其中:mb，=(，z)和分别为电子的带质量，坐标和动量;V()和V(z)分别表示量子盘x-y平面和z方向的限定势，

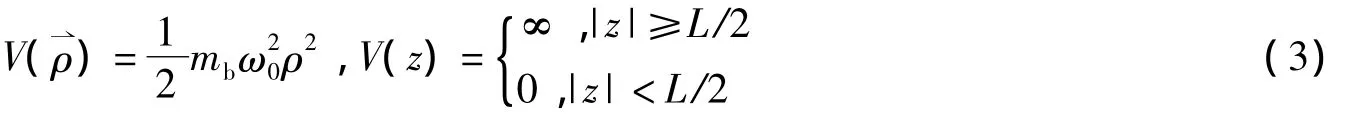
其中:ω0为量子盘的横向受限强度。根据文献［19］和［20］的讨论可知，当z方向的限制比x-y方向的限制大得多的情况下，在z方向仅有最低的电子副带被占据，则z方向与x-y平面没有耦合，那么上述3D问题就可以精确的用一个2D问题来近似。

(1)式中第二项

(1)式中最后一项

是电子-LO声子相互作用项，式中Vk为相互作用的傅里叶系数，

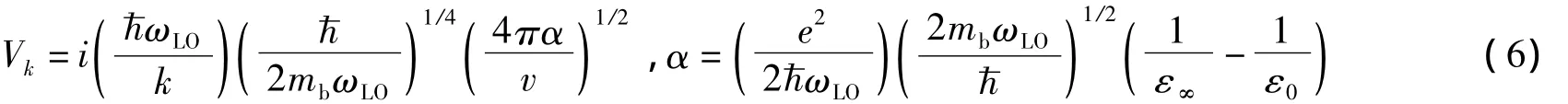
其中:v是晶体的体积，α为电子-LO声子耦合强度，ε∞和ε0分别是高频和静态介电常数。

为了讨论量子盘中磁极化子的效哈密顿量，首先，对电子x-y平面的动量和坐标引入Huybrechts线性组合算符［21］

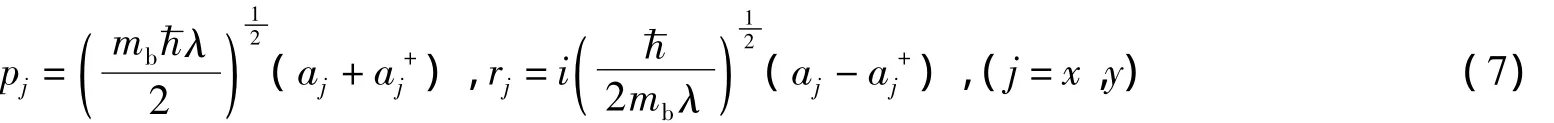
式中λ是变分参数。其次，再讨论算符函数U－1HU2在|Ψ〉态中的期待值。按照变分原理

这里

是 Lee-Low-Pines(LLP)幺正变换［22］。其中，fk和是变分参数。

是磁极化子的试探波函数。其中:φl(z)，…)为电子 z方向的波函数，|0〉b为零声子态，|0〉a为极化子基态，由bk|0〉b=0，aj|0〉a=0确定。

将式(1)～(7)和式(9)、(10)代入式(8)，可确定变分参数λ和fk()。其中λ满足

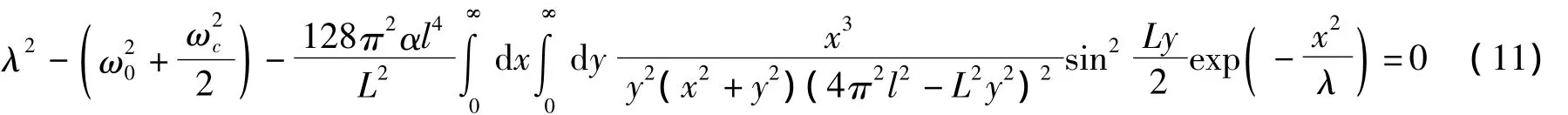
利用这些变分参数可以算出磁极化子的基态能量和基态波函数为

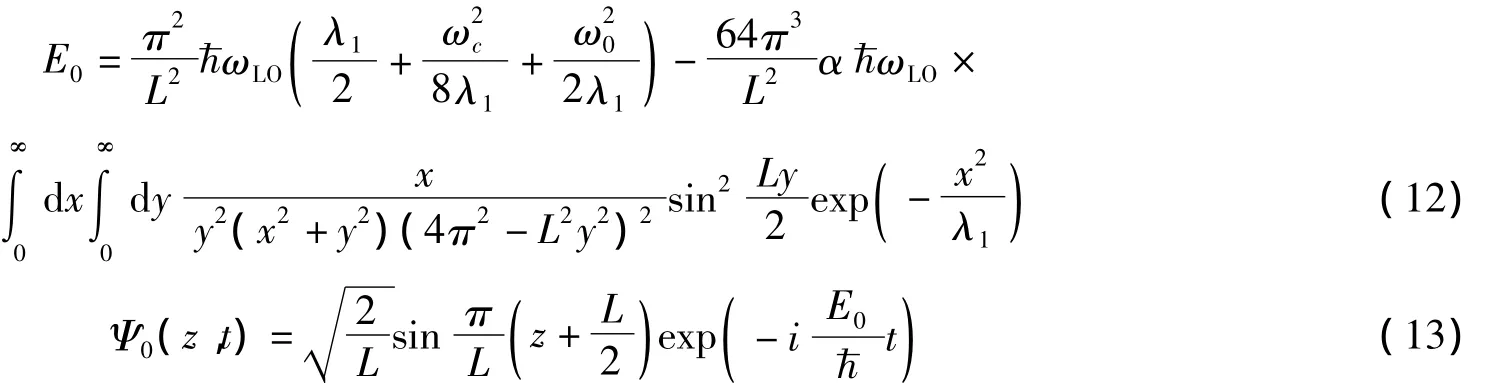
磁极化子的第一激发态能量和波函数为

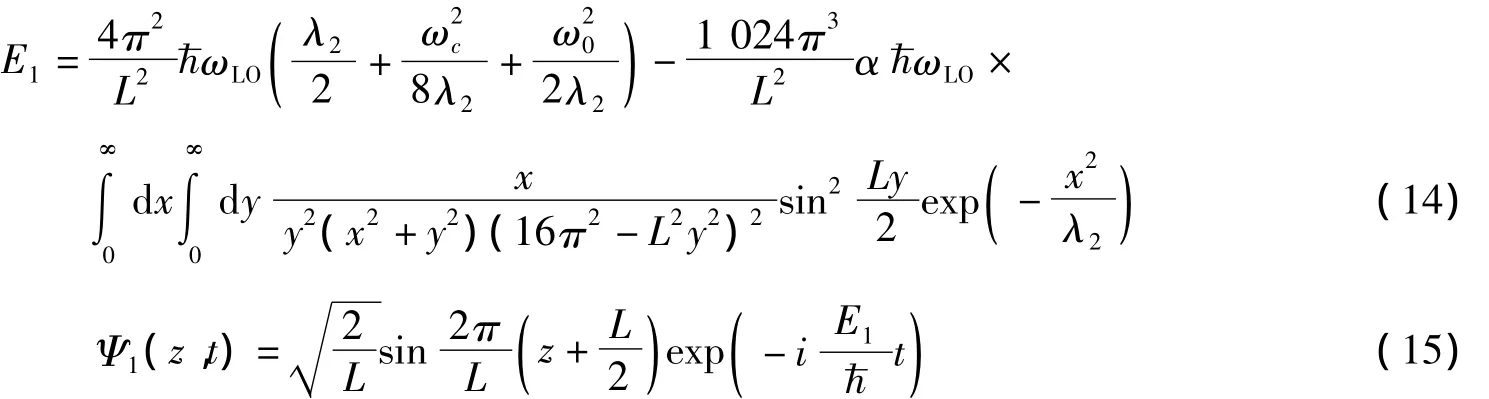
其中:λ1，λ2是方程(11)对应l=1，2的两个根。由此，可以构造一个二能级体系，当电子处于这样一个叠加态 Ψ(z，t)=(Ψ1+Ψ2)/时，即构成一个量子点量子比特。量子比特内电子的几率分布为

它随时间t做周期性振荡的周期T0为

2 结果与讨论

为了直观地了解外磁场、LO声子效应和量子盘量子尺寸效应对强耦合磁极化子量子比特的影响，在此给出了数值计算结果，如图1～图3。图中各量采用极化子单位(2mb==ωLO=1)。

图1描述了磁极化子的基态和第一激发态振动频率λ1(虚线)和λ2(实线)在不同受限强度ω0下随回旋频率ωc的变化(图1(a))，不同耦合强度α下随量子盘厚度L的变化(图1(b))。由图1可以看出，在相同ω0，λ1＞λ2，这表明当体系处于基态时声子被激发的几率要比激发态大一些，这一结果符合物理实际，否则就发生所谓“粒子(声子)数反转”的反常现象。另外，λ1和λ2随ωc的增加而增大。这表明，外磁场导致电子-晶格的极化场加强，使电子与更多声子相互作用，进而导致磁极化子振动频率的增大。由图1(a)可以看出，ω0对λ1和λ2随ωc的变化产生显著影响，当ωc给定时，λ1和λ2随ω0的增加而增大，增大的幅度(即λ1～ωc和λ2～ωc曲线的斜率)随ω0的增加而减小。这是因为，随着量子点限定势(ω0)的增大，以声子为媒介的电子-声子之间相互作用由于粒子运动范围缩小而增强，使电子与更多声子相互作用，导致磁极化子的声子平均数增多。从图1(b)可以看出，λ随L的增加而减小。这是因为，随着量子盘厚度的增大，电子热运动和电子-声子相互作用因粒子纵向运动空间的增大而减弱，致使磁极化子的平均声子数减小，表现了量子盘奇特的量子尺寸效应。从图1(b)也不难看出，当L给定时，λ1和λ2随α的增加而增大。这是因为，α越大意味着电子-声子相互作用越强，进而导致磁极化子振动频率的增大。

图2描写了量子比特振荡的周期T0在不同受限强度ω0下随回旋频率ωc的变化(图2(a))，不同耦合强度α下随量子盘厚度L的变化(图2(b))。由图2(a)可以看出，T0随ω0的增大而增加，T0随ωc的变化规律受ω0的影响较大。当ω0较小时，T0随ωc的增加而先振荡减小后振荡增大;当ω0较大时，T0随ωc的增加而小幅振荡增大。这是由于能级E1和E0随ωc的增加而增大的幅度与ω0的大小有关所致。这表明，可以通过实验来控制量子点的大小或外加电磁场来改变能级间距，从而得到满足构造量子比特要求的磁极化子能态。由图2(b)可以看出，T0随L的增加而增大，这是由能级差E1－E0随L的增加而减小所致。另外，由图2(b)还可以看出，电声子相互作用对量子比特振荡的周期T0的影响(虚线)不可忽略，电声子相互作用将导致T0下降，T0随α增加而减小。这是由于随着耦合强度的增加，由于激发态的电子-声子耦合的强度比基态的电子-声子耦合的强度弱，使第一激发态与基态之间能级差增加，而造成振荡周期的减小。

图3描写了量子比特内电子的几率分布ρ。(a)在不同受限强度ω0下随磁场的回旋频率ωc的变化(图3(a));在考虑与不考虑电声子耦合α时随量子盘厚度L的变化(图3(b));(c)不同纵向坐标z下随时间t的变化(图3(c));不同时间t下随纵向坐标z的变化(图3(d))。由图3(a)可以看出，ρ随ω0的增加而减小。对照图2(a)与图3(a)不难发现一有趣现象，ρ随ωc的变化规律与T0随ωc的变化规律恰好相反，即当ω0较小时ρ随ωc的增加而先振荡增大后振荡减小;当ω0较大时ρ随ωc的增加振荡减小。由图3(b)可以看出，ρ随L的增加总体上是振荡减小，这符合一般量子阱中粒子的几率分布规律。不过从图3(b)还可以看出，考虑与不考虑声子效应对ρ随L的增加而起伏变化影响较大:当不考虑声子效应(实线)时，ρ随L的增加而小幅振荡并迅速减小;当考虑声子效应(虚线)时，电子的波动性加强，ρ随L的增加而起伏增多并受电声子耦合强度α影响显著。从图3(c)和图3(d)可以看出，ρ不同纵向坐标z下随时间t以及在不同时间t下随纵向坐标z的变化呈现出显著的量子效应。

图1 振动频率λ在不同受限强度ω0下随回旋频率ωc的变化(a)，不同耦合强度α下随量子盘厚度L的变化(b)虚线和实线分别表示基态和第一激发态的振动频率

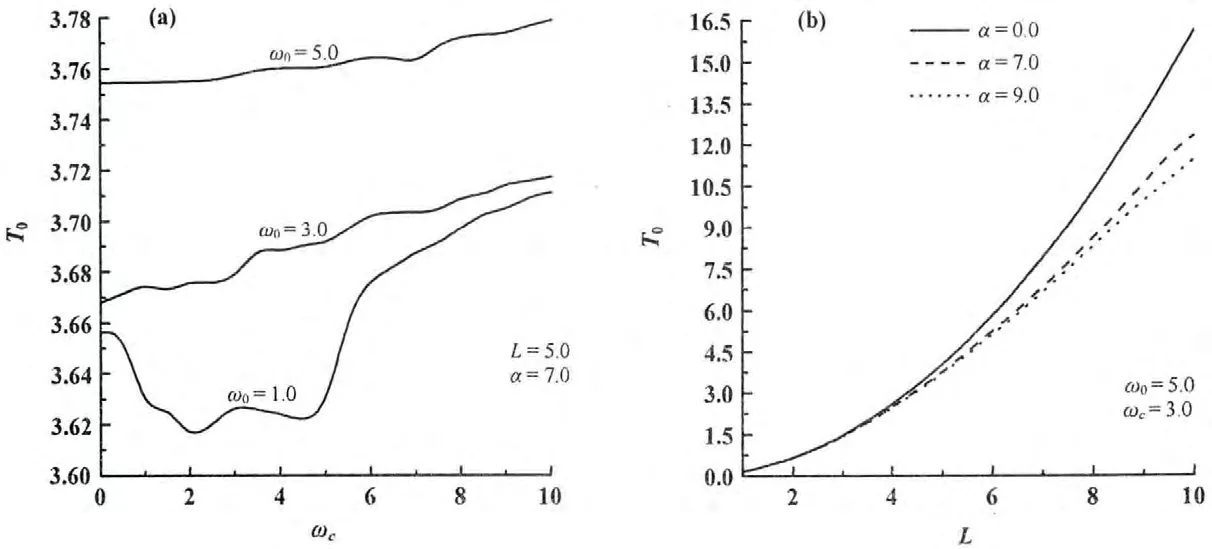
图2 振荡的周期T0在不同受限强度ω0下随回旋频率ωc的变化(a)，考虑与不考虑电子-声子耦合时随量子盘厚度L的变化(b)

3 结 论

本次研究采用Lee-Low-Pines-Huybrechts变分方法研究了外磁场、LO声子效应和量子点厚度对量子盘中电子-LO声子强耦合磁极化子的振动频率和qubit的影响。结果表明:(1)磁极化子基态的振动频率大于激发态的振动频率，λ随ωc和α的增加而增大，随L的增加而减小;(2)量子比特振荡的周期T0随受限强度ω0和量子盘厚度L的增加而增大，随耦合强度α的增加而减小;(3)量子比特内电子的几率分布ρ随ω0的增加而减小，随L的增加振荡减小;(4)T0和ρ随ωc的变化规律相反且受ω0和α的影响显著。

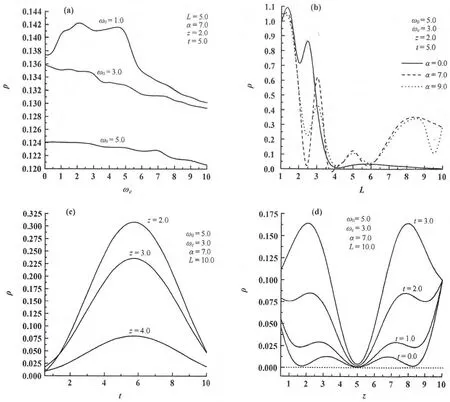
图3 几率分布ρ在不同受限强度ω0下随磁场的回旋频率ωc的变化(a);不同耦合强度α下随量子盘厚度L的变化(b);不同纵向坐标z下随时间t的变化(c);不同时间t下随纵向坐标z的变化(d)

［1］ Cirac J I，Zoller P.Quantum computations with cold trappedions［J］.Phys Rev Lett，1995，74:4 091-4 094.

［2］ Gershenfeld N A，Chuang L.Bulk spin-resonance quantum computation［J］.Science，1997，275:350-356.

［3］ Kane B E.A sIlicon-based nuclear spin quantum computer［J］.Nature，1998，393:133-137.

［4］ Makhlin Y，Schon G，Shnirma A.Josephson-junction qubitwith controlled ccuplings［J］.Nature，1999，398:305-307.

［5］ Jordan K，Stephen JP.Coherent rotations of a single spin-based qubit in a single quantum dotat fixed Zeeman energy［J］.Phys Rev B，2005，71:125 332-125 336.

［6］ Furuta S，Barnes CHW，Doran C JL.Single-qubit gates and measurements in the surface acoustic wave quantum computer［J］.Phys Rev B，2004，70:205 320-205 331.

［7］ Li SS，Long G L，Bai F S，et al.Quantum computing［J］.Pro Natl Acad Sci USA，2001，98(21):11 847-11 850.

［8］ Li SS，Xia JB，Yang F H，et al.InAs/GaAs single-electron quantum dot qubit［J］.Journal of Applied Physics，2001，90(12)6 151-6 155.

［9］ Liang SD，Chen C Y，Jiang SC，et al.Size effect on exciton-phonon scattering in quantum wires［J］.Phys Rev B，1996，53:15 459-15 464.

［10］ Fai LC，Teboul V，Monteil A，etal.Polaron in a quasi1D cylindricalquantum wire［J］.Condensed Matter Physics，2005，8:639-650.

［11］ Wu Z J，Zhu K D，Yuan X Z，etal.Deterministic quantum state transfer from an electronic charge qubit to a photonic polarization qubit［J］.Phys Rev B，2005，71:205 323-205 327.

［12］ LiW P，Yin JW，Yu Y F，etal.The effectofmagnetic on the properties of a parabolic quantum dotqubit［J］.JLow Temper Phys，2010，160:112-118.

［13］ Yu Y F，LiW P，Yin JW，et al.The decoherence of single electron quantum dot qubit［J］.Int JMod Phys B，2011，50:3 322-3 328.

［14］ Sun Y，Ding Z H，Xiao JL.Effects ofmagnetic field on the coherence time of a parabolic quantum dot qubit［J］.J Low Temper Phys，2014，177:151-156.

［15］ Kash K，Scherer A，Worlock JM，et al.Optical spectroscopy of ultrasmall structures etched form quantum wells［J］.Appl Phys Lett，1986，49:1 043-1 045.

［16］ Reed MA，Randall JN，Aggarwal R J，etal.Obser vation of discrete electr onic states in a zero-dimensional semiconductor nanostructure［J］.Phys Rev Lett，1988，60:535-537.

［17］ Chen C Y，LiW S，Teng X Y，et al.Polaron in a quantum disk［J］.Physica B，1998，245:92-102.

［18］ Fafard S，Leonard D，Merz JL，et al.Electron and hole energy levels in InAs self assembled quantum dots［J］.Appl Phys Lett，1995，66:1 767-1 769.

［19］ Peeters FM，Schweigert V A.Two-electron quantum disks［J］.Phys Rev B，1996，53(3):1 468-1 474.

［20］ Price R，Zhu X，Sarma SD，et al.Laughlin-liquid-Wigner-solid transition at high density in wide quantum wells［J］.Phys Rev B，1995，51(3):2 017-2 021.

［21］ Tokuda N.A variational approach to the polaron problem［J］.JPhys C:Solid State Phys，1980，13:L 851-L 855.

［22］ Lee TD，Low FM，Pines D.Themotion of slow electrons in a crystal［J］.Phys Rev，1953，90:297-302.

［23］ Xiao W，Xiao JL.The effectivemass of strong-couplingmagnetopolaron in quantum dot［J］.Int JMod Phys B，2007，21:2 007-2 016.