对数学分析教学中两个问题的探讨

左俊梅 何奇龙

（周口师范学院数学与统计学院 河南周口 466001）

对数学分析教学中两个问题的探讨

左俊梅 何奇龙

（周口师范学院数学与统计学院 河南周口 466001）

给出对分段函数求导数的两种方法；对洛必达法则的使用给出几点说明。

分段函数；求导；洛必达法则

下面结合我对数学分析教学的实践，就分段函数求导和洛必达法则的使用这两个方面的问题进行详细的探讨。

一、分段函数求导数的方法

对于一般的函数，我们可用求导法则进行求导运算，但对于分段函数，求导过程略显麻烦。其求导秉承的宗旨是整段上的函数导数直接求，分段点处的导数单独求，在讲导数定义时，我们首先接触了用定义来求分段函数分段点处的导数。

1。定义法

依次为依据，我们可以判定分段函数在分段点处的导数存在情况。

2。利用导数极限定理

二、洛必达法则运用时的注意事项

(2)不能对任何比式的极限都按洛必达法则求解，首先必须注意它是不是不定式极限，其次要验证它是否满足洛必达法则的其他条件。

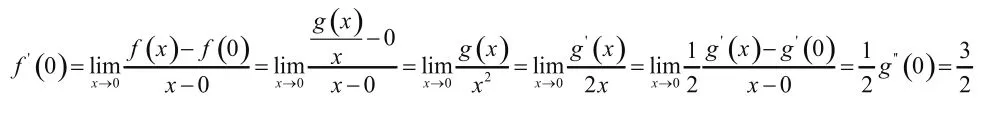
[1]华东师范大学数学系编.数学分析(上册)[M].北京:高等教育出版社,1991.

Discussion on two problems in the teaching of mathematical analysis

Zuo Jun-mei, He Qi-long

(College of Mathematics and Statistics, Zhoukou Normal University, Zhoukou Henan, 466001, China)

This paper presents two methods for the derivative of piecewise function; L'Hospital Rule are presented using several points. Key words: piecewise function; derivative; L'Hospital Rule

G642

A

1000-9795（2014）06-0190-01

［责任编辑：刘丽杰］

2014-03-03

左俊梅（1986-），女，河南周口人，助教，从事分形几何与小波分析研究。

何奇龙（1985-），男，河南郸城人，助教，从事金融数学方向的研究。