复杂网络的有限时间同步控制

于 镝，白雪峰，任伟建，康朝海

(1.东北石油大学电气信息工程学院，黑龙江大庆163318;2.哈尔滨医科大学(大庆校区)医学信息学院，黑龙江大庆163319)

0 引言

近年来，由于复杂网络大量存在于自然界和人类社会生活中，如WWW、城市交通网、生物代谢网络和大型电力网络等，所以复杂网络研究引起众多领域学者的极大关注［1-5］。同步是一类十分重要的非线性现象，并且历史悠久，而复杂网络同步由于其广泛的应用前景而倍受研究人员的青睐。目前，复杂网络渐近同步取得了丰富的研究成果［6-14］。文献［6］对线性耦合常微分方程所描述的系统，考虑存在耦合与非耦合并存时，通过矩阵特征值分析得到局部和全局同步的充分条件。文献［7］由若干相同结点线性耦合组成的复杂动力学系统，通过同步状态线性化，用主稳定函数法判断同步流形稳定性实现复杂系统的局部和全局同步。文献［8］利用邻近结点信息与度值最大的结点相连耦合实现网络同步优化。文献［9］考虑了无向网络且耦合结点均为线性情况时的同步控制，并总结归纳出同步控制与网络协调控制在本质上是一致的，进而为复杂网络同步控制开辟了新的控制思路。牵引控制是复杂网络同步控制的有效方法之一［10-15］。其中文献［12］对一类线性耦合复杂网络证明了通过足够大的耦合度，仅牵制部分节点即可实现整个网络的同步。更有趣的是，文献［13］提出了只应用一个控制器的牵制控制方案实现网络同步。文献［14，15］则对一般耦合复杂网络提出线性控制协议，给出网络实现同步的充分条件，并引入耦合强度和控制增益的自适应控制机制，提出了更为灵活的控制方案。

以上成果大都是关于复杂网络的渐近同步，即网络在无限时间内达到同步。在实际应用中，复杂网络同步通常需要在有限时间内实现。因此，对于复杂网络有限时间同步的研究具有重要的理论意义和应用价值，但该方面的研究成果较少。受多智能体网络有限时间协调控制［16-20］的启发，笔者针对复杂动态网络有限时间同步问题，提出非光滑控制协议，并给出实现有限时间同步的充分条件。

1 问题描述

考虑一类由N个节点构成的复杂网络，第i个节点动态描述如下

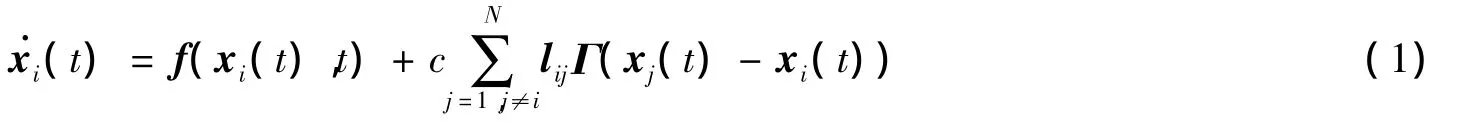
复杂网络同步解s(t)可以是一个平衡点、周期轨迹或混沌轨迹。复杂网络(1)的有限时间同步问题描述如下。

定义1 若存在时刻t*＞0且对于∀i，j和t≥t*都有‖xi(t)-s(t)‖=0，则称该复杂网络实现了有限时间同步。

笔者的目标是设计合适的反馈控制律，使复杂网络(1)在该控制下实现有限时间同步。在给出主要结果前，先给出如下假设和引理。对于网络(1)各个节点动态满足下面假设。

假设1 存在常值矩阵K，使

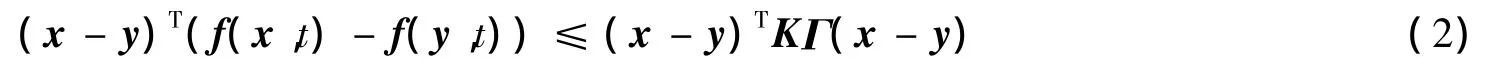
引理1［19］考虑如下微分方程

其中c＞0，0＜α＜1，则函数 x(t)将会在有限时间内收敛到零点，且对于所有t≥t*，有x(t)=0。

引理 2［20］令xi∈ (i=1，2，…，N)，0 ＜ α ＜1。若xi≥0 且，则

2 主要结果

为实现复杂网络系统(1)各节点同步，提出非光滑连续控制协议，并基于有限时间稳定性引理，给出复杂动态网络(1)实现有限时间同步的充分条件。不失一般性，令第i=N个节点作为驱动节点，则受控复杂网络描述为

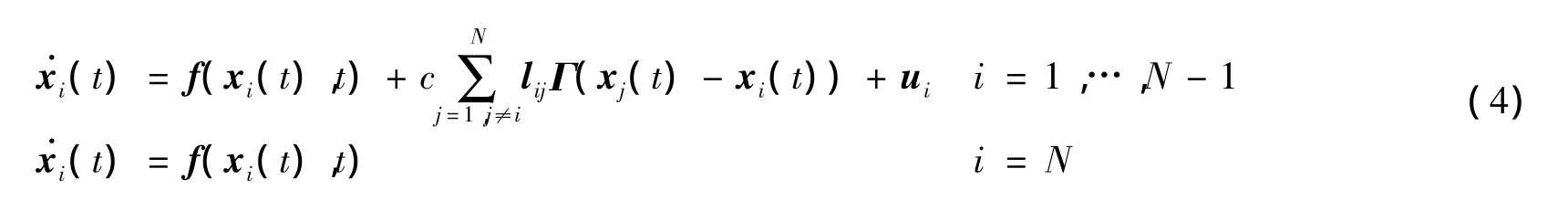
其中ui为第i个节点的控制协议，在ui控制作用下使复杂动态网络(1)在t≥t*时实现x1(t)=x2(t)=…=xN(t)，即实现网络的有限时间同步。

定义同步误差为ei(t)=xi(t)-xN(t)，i=1，…，N，则定义ε(t)=［e1(t)，…，eN(t)］T为网络误差矢量。分别设计两种不同的控制协议为

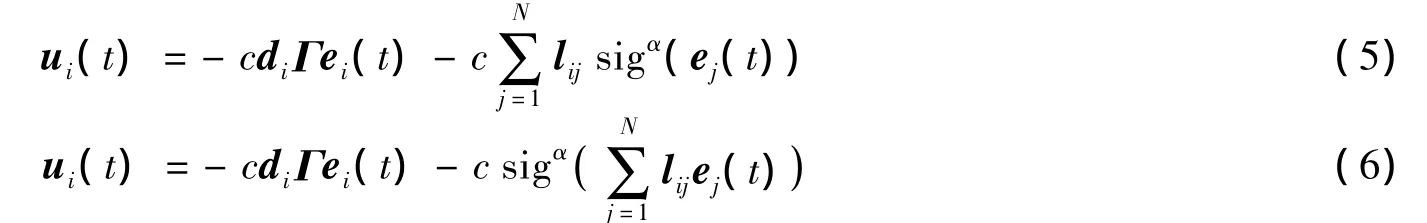
其中i=1，…，N-1，函数)，z=［z1，…，zn］T，0 ＜ α ＜1，且 sigα(z)=［sigα(z1)，…，sigα(zn)］T。di为控制增益，则在控制协议(5)和协议(6)的作用下，网络误差动态分别为

其中i=1，…，N-1。

定理1 考虑由式(1)描述的复杂动态网络，令假设1成立，节点之间无向连通，在控制协议(5)的作用下，若λmax［‖K‖IN+c(L-D)］≤0(其中λmax(·)为矩阵的最大特征值)，则网络(1)实现有限时间同步。其中D=diag{d1，…，dN-1，0}，L为节点之间的外部耦合矩阵。

证明 考虑如下Lyapunov函数

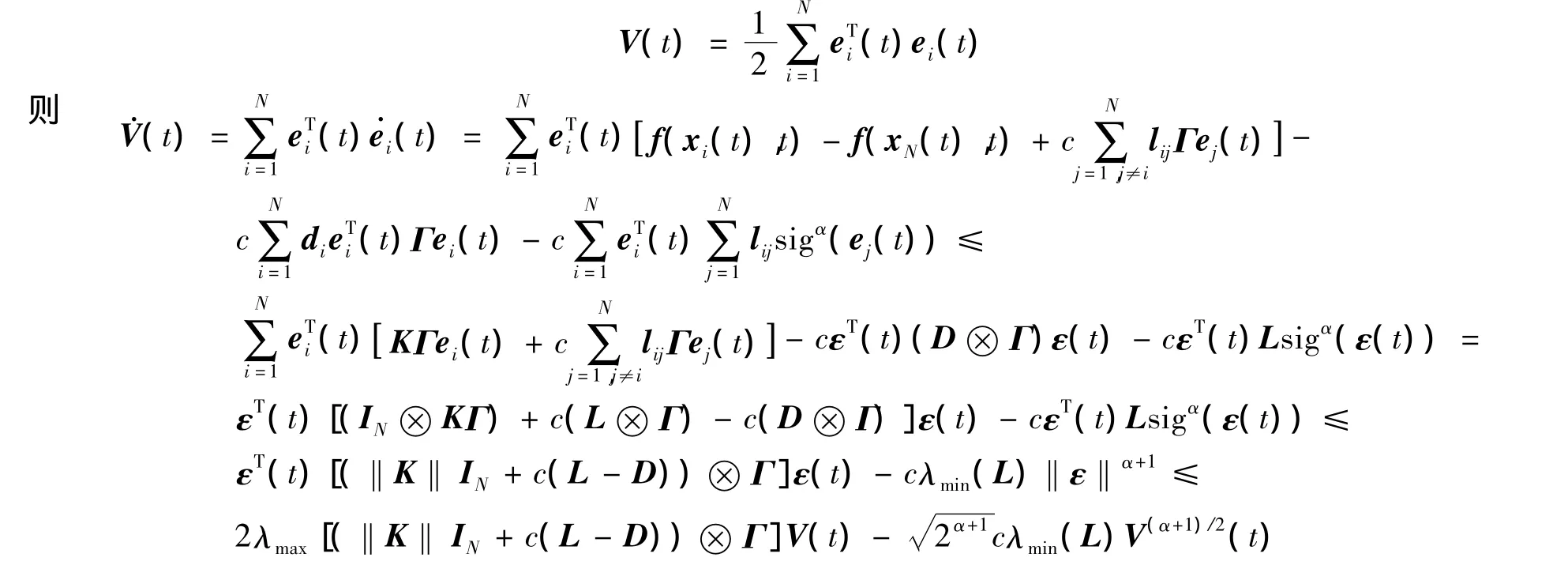
第1个不等式由假设1得出，第2个不等式由引理2和矩阵性质‖K‖IN≥K，K∈n×n得到。则当λmax［‖K‖IN+c(L-D)］≤0时，由Γ正定和引理1可得，网络误差在有限时间

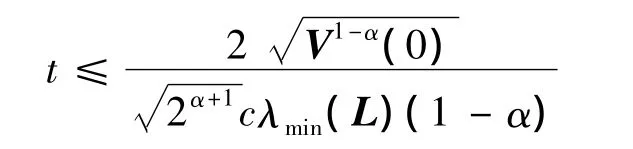
内达到零，则网络(1)可在有限时间内达到同步。

定理2 考虑由(1)描述的复杂动态网络，令假设1成立，节点间无向连通，在控制协议(6)的作用下，若λmax［‖K‖IN+c(L-D)］≤0，则网络(1)同样可实现有限时间同步，并且有限时间为

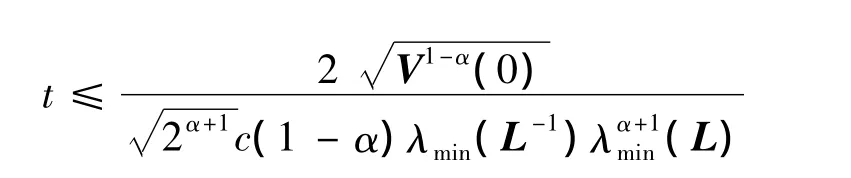
证明 考虑如下Lyapunov函数

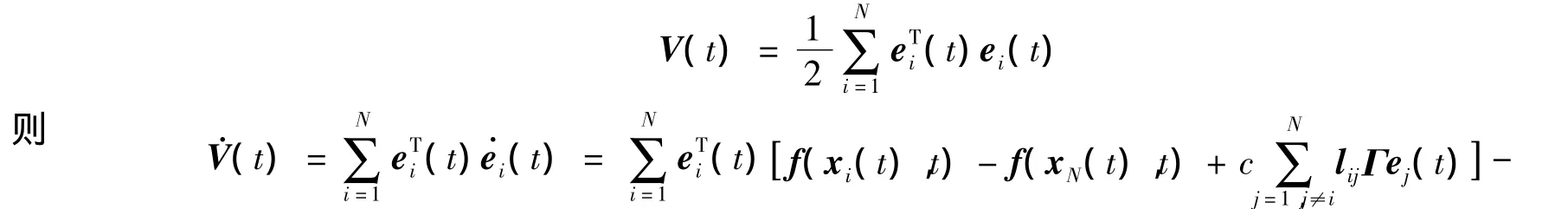
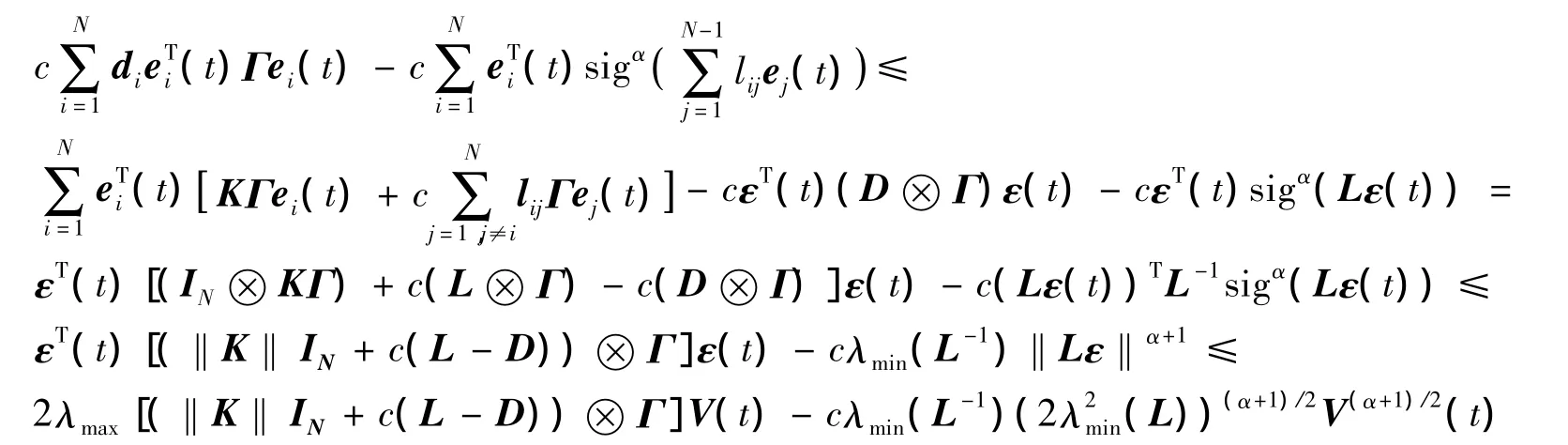
前面与定理1证明过程类似，只有最后一步根据下面的推导得证。令λi为L的特征值，同时wi为相应于λi的特征向量，令{wi}为N中的一组标准正交基。令，可得，进一步有，则有。当时，由引理1可得，网络误差在有限时间

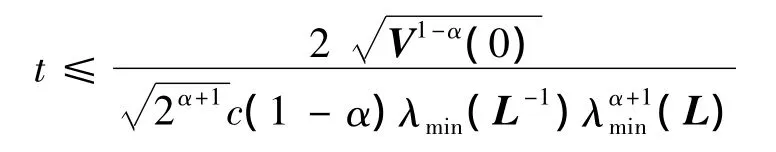
内达到零，即网络(1)可在有限时间内达到有限时间同步。

3 仿真研究

Chen系统和Lü系统是典型的复杂网络，并且其同步研究在保密通信、信号处理和生命科学等方面有着十分广阔的应用前景，引起了广大学者的极大关注。下面就针对这两个复杂网络分别进行有限时间同步仿真研究。

实例1 首先考虑由5个Chen系统所构成的复杂网络(1)。其中非线性特性描述如下

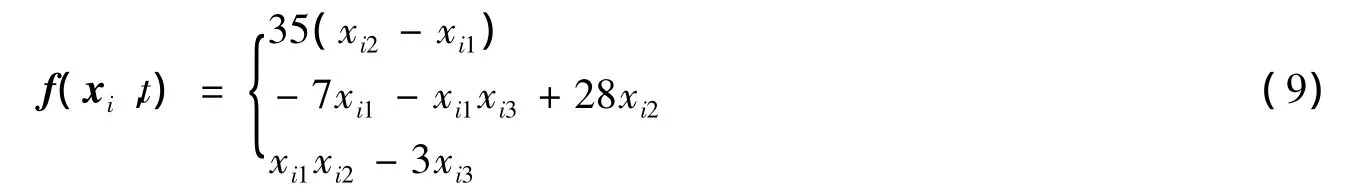
其中 xi=［xi1，xi2，xi3］T，取第 5 个节点作为驱动点，令‖K‖ =30.934 2［14］，D=diag{3.8，6，8，6，0}，c=32，内部和外部耦合矩阵分别取为

则在控制协议(5)和协议(6)的作用下，网络同步误差曲线分别如图1和图2所示。由仿真图形可知，大约在t=0.6 s后网络同步误差趋于零，网络(1)实现有限时间同步。

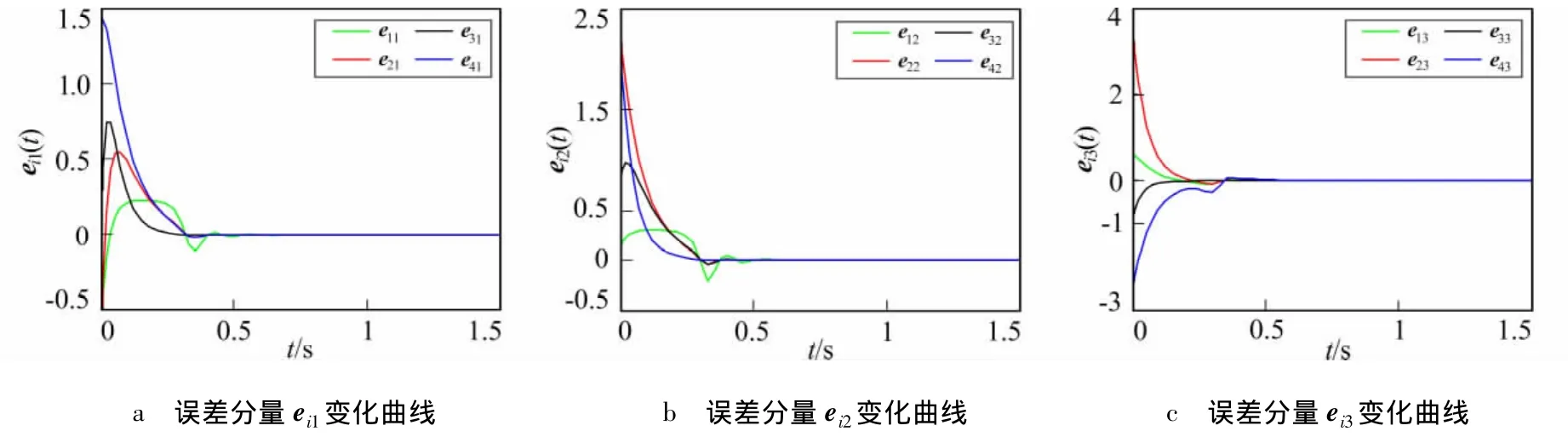
图1 Chen网络同步误差曲线(控制协议(5)作用下)Fig.1 Synchronization error curves of Chen networks(under the action of control protocol(5))

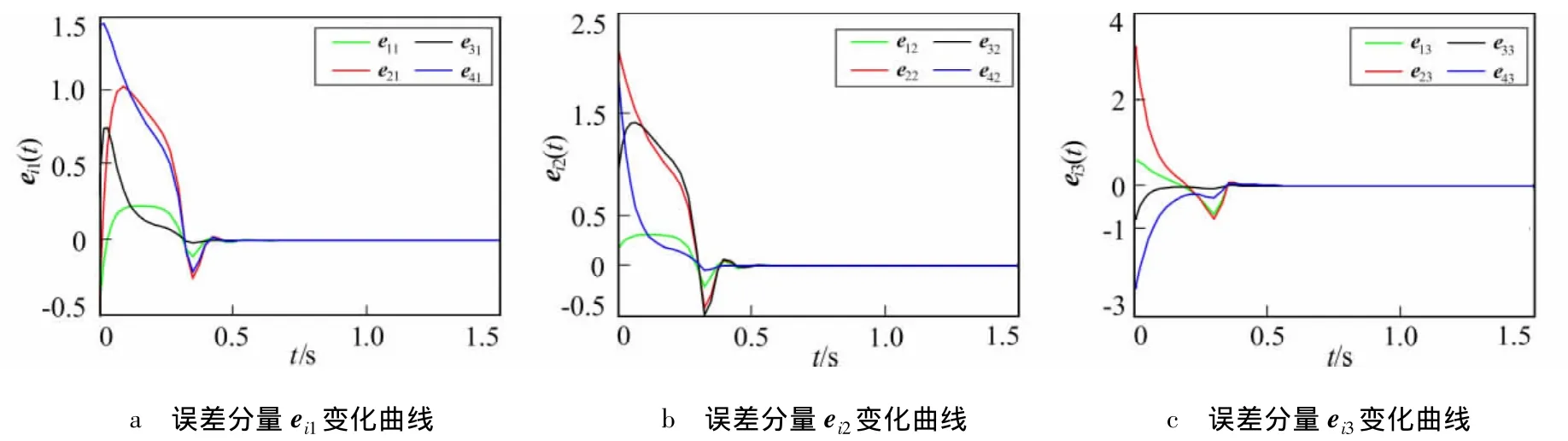
图2 Chen网络同步误差曲线(控制协议(6)作用下)Fig.2 Synchronization error curves of Chen networks(under the action of control protocol(6))

实例2 考虑由5个Lü系统所构成的复杂网络(1)。其中非线性特性描述如下

取第5 个节点作为驱动点，且‖K‖ =16.278 7［21］，D=diag{4，4，4，4，0}，c=17，内部和外部耦合矩阵同上。则在控制协议(5)和协议(6)的作用下，网络同步误差曲线分别如图3和图4所示。由仿真图形可知，大约在t=0.2 s后网络同步误差趋于零，网络(1)实现有限时间同步。

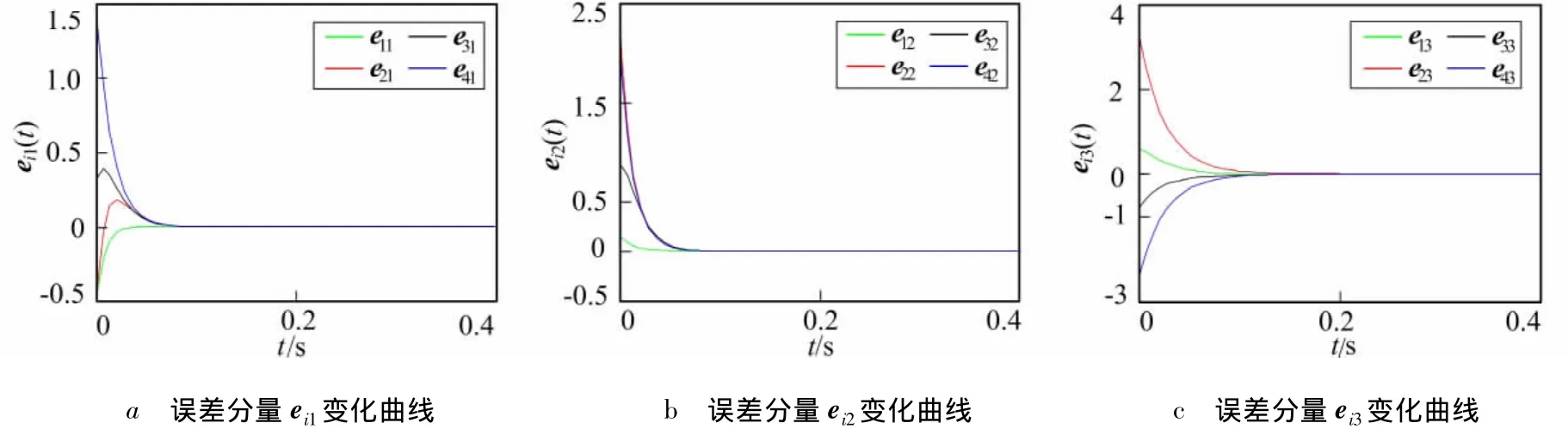
图3 Lü网络同步误差曲线(控制协议(5)作用下)Fig.3 Synchronization error curves of Lü networks(under the action of control protocol(5))

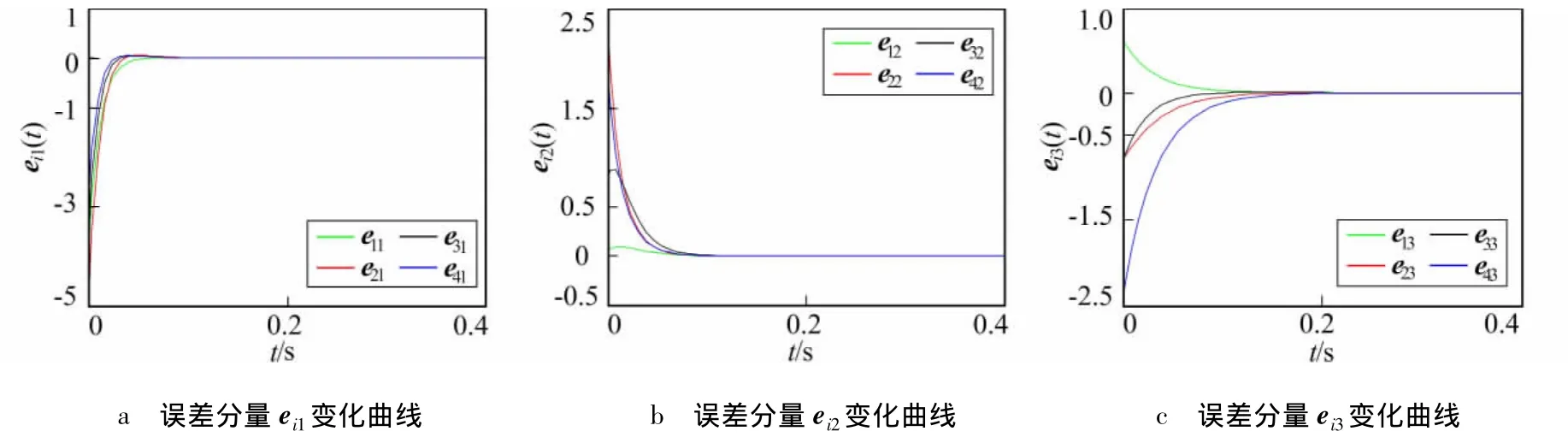
图4 Lü网络同步误差曲线(控制协议(6)作用下)Fig.4 Synchronization error curves of Lü networks(under the action of control protocol(6))

在上述复杂网络有限时间同步仿真研究过程中，控制增益矩阵D的取值决定网络有限时间收敛的快速性，但同时也影响收敛过程中同步误差的大小。如果控制增益矩阵D中的元素选取较大数值，则能得到快速的有限时间收敛的同步误差曲线，但此时同步误差振荡幅度较大。所以需要选取合适的控制增益得到既快速又振荡适度的收敛过程。

4 结 语

笔者针对具有线性耦合的复杂动态网络有限时间同步问题，提出非光滑连续控制协议，并基于有限时间稳定性引理，给出了实现有限时间同步的充分条件。在复杂网络同步过程中，网络同步不仅受网络拓扑和结点之间耦合影响，而且在控制协议中加入非线性函数使复杂网络同步特性得到改善，通过仿真实例验证了所提方案的可行性和有效性。下一步将研究不确定复杂网络的有限时间同步问题。

［1］BELYKH I，DI BERNARDO M，KURTHS J，et al.Evolving Dynamical Networks［J］.Physica D:Nonlinear Phenomena，2014，267(1):1-6.

［2］张志颖，冯秀琴，姚治海，等.运动光格玻色-爱因斯坦凝聚体的混沌同步［J］.吉林大学学报:理学版，2012，50(4):779-784.ZHANG Zhiying，FENG Xiuqin，YAO Zhihai，et al.Chaotic Synchronization of Bose-Einstein Condensed Body in Moving Optical Lattices［J］.Journal of Jilin University:Science Edition，2012，50(4):779-784.

［3］赵明，周涛，陈关荣，等.复杂网络上动力系统同步的研究进展Ⅱ——如何提高网络的同步能力［J］.物理学进展，2008，28(1):23-31.ZHAO Ming，ZHOU Tao，CHEN Guanrong，et al.A Review on Synchronization of Dynamical Systems on Complex NetworksⅡ:How to Enhance the Network Synchronizability［J］.Progress in Physics，2008，28(1):23-31.

［4］姜玉秋.Lorenz混沌系统的线性同步控制［J］.吉林大学学报:信息科学版，2011，29(6):571-575.JIANG Yuqiu.Linear Synchronization Control of Lorenz Chaos Systems［J］.Journal of Jilin University:Information Science Edition，2011，29(6):571-575.

［5］梅蓉.时滞三角型混沌系统的滑模自适应同步控制方法［J］.吉林大学学报:信息科学版，2013，31(1):18-24.MEI Rong.Sliding-Mode Adaptive Synchronization Control for Delayed Triangle Chaotic System ［J］.Journal of Jilin University:Information Science Edition，2013，31(1):18-24.

［6］LU Wenlian，CHEN Tianping.New Approach to Synchronization Analysis of Linearly Coupled Ordinary Differential Systems［J］.Physica D:Nonlinear Phenomena，2006，213(2):214-230.

［7］樊炳航，孙鹤旭，张华，等.网络型耦合复动力系统的同步动力学［J］.复杂系统与复杂性科学，2012，9(1):72-77.FAN Binghang，SUN Hexu，ZHANG Hua，et al.Synchronization Dynamics in Networked Coupled Complex Dynamical Systems［J］.Complex Systems and Complexity Science，2012，9(1):72-77.

［8］FENG Junliang，ZHAO Ming，LAI Choyheng.Synchronization Optimal Networks Obtained Using Local Structure Information［J］.Physical A，Statistical Mechanics and Its Applications，2012，391(21):5280-5281.

［9］LI Zhongkui，DUAN Zhisheng，CHEN Guanrong，et al.Consensus of Multi-Agent Systems and Synchronization of Complex Networks:A Unified Viewpoint［J］.IEEE Transactions on Circuits and Systems Ⅰ:Regular Papers，2010，57(1):213-224.

［10］YANG Huizhong，LI Sheng.Pinning Control of A Generalized Complex Dynamical Network Model［J］.Journal of Control Theory and Applications，2009，7(1):1-7.

［11］ZHANG Qingzhen，LI Zhongkui.Pinning Control of Complex Lur＇e Networks ［J］.Chinese Physics B，2009，18(6):2176-2181.

［12］QIN Jiahu，ZHENG Weixing，GAO Huijun.A Study of Synchronization of Complex Networks via Pinning Control［C］∥Proceeding of International Symposium on Circuits and Systems.Brazil:［s.n.］，2011:1596-1598.

［13］GUO Wanli.Pinning Complex Networks by a Single Controller on One Element of a Node ［J］.Journal of Computational Information Systems，2012，8(19):7865-7872.

［14］YU Wenwu，CHEN Guanrong，LÜ Jinhu.On Pinning Synchronization of Complex Dynamical Networks［J］.Automatica，2009，45(2):429-432.

［15］WANG Weiping，LI Lixiang，PENG Haipeng.Adaptive Synchronization of Complex Dynamical Multi-Links Networks with Similar Nodes［J］.Mathematical Problems in Engineering，2013(3):1-12.

［16］WANG Long，FENG Xiao.Finite-Time Consensus Problems for Networks of Dynamic Agents［J］.IEEE Transactions on Automatic Control，2010，55(4):950-955.

［17］SHANG Yilun.Finite-Time Consensus for Multi-Agent Systems with Fixed Topologies［J］.International Journal of Systems Science，2012，43(3):499-506.

［18］YANG Shaofu，CAO Jinde，LU Jianquan.A New Protocol for Finite-Time Consensus of Detail-Balanced Multi-Agent Networks［J］.Chaos:An Interdisciplinary Journal of Nonlinear Science，2012，22(4):043134.

［19］CORTÉS J.Finite-Time Convergent Gradient Flows with Applications to Network Consensus［J］.Automatica，2006，42(11):1993-2000.

［20］于镝，伍清河，王垚.非线性网络有限时间分布式跟踪控制［J］.控制与决策，2013，28(10):1491-1496.YU Di，WU Qinghe，WANG Yao.Finite Time Distributed Tracking Control of Nonlinear Networks［J］.Control and Decision，2013，28(10):1491-1496.

［21］梁义，王兴元.基于低阶矩阵最大特征值的复杂网络牵制混沌同步［J］.物理学报，2012，61(3):532-539.LIANG Yi，WANG Xingyuan.Pinning Chaotic Synchronization in Complex Networks on Maximum Eigenvalue of Low Order Matrix［J］.Acta Physica Sinica，2012，61(3):532-539.