α-幂过程下阈值为几何过程的冲击模型

杜倩男，吴清太，黄 凯

(南京农业大学理学院，江苏南京210095)

早期的维修模型研究中，大部分考虑完美维修模型，即系统是“修复如新”的.然而，在实际情况中，系统的失效修理是“修复非新”的，系统修理后的寿命逐渐递减，与此同时系统的修理时间会越来越长，并最终不能再工作，也不能再被修理，称这样的系统为退化系统.文献［1-2］中用一种单调的几何过程来模拟这种随机现象.文献［3-5］利用几何过程对单部件可修系统进行了研究.文献［6］中将最优更换策略引入可靠性研究中.文献［7］中提出了一种全新的单调过程，即α-幂过程，并发现该过程与几何过程具有相似的性质.文献［8］中研究了退化系统的α-幂过程维修模型的最优更换策略的单调性，根据最优更换策略关于某一参数的单调过程，当参数改变时，相应地改变更换策略.文献［9］中利用α-幂过程对一类退化系统进行了研究，采用更换策略N，得到系统长期运行下的平均费用率表达式，找到了相应的最优更换策略N*，并验证了最优更换策略的存在性和唯一性.

一些文献只假设系统失效时由于内部因素，如衰老和退化造成的，然而在实际过程中，外部冲击也可能引起系统的失效，例如，一个计算机系统就可能由于外部病毒的入侵而引起计算机系统的失效．文中把病毒入侵看作是外部冲击，冲击模型是可靠性理论中的主要模型之一，它主要分成3类:累积冲击模型、极值冲击模型和δ-冲击模型．而文中主要研究极值冲击模型，即单次冲击对系统的影响相互独立，当某次冲击的冲击量太大，超过了系统的阈值时，系统就会失效［10］．

以上文献大多研究系统失效仅由冲击引起，但有时系统失效不仅由外部冲击引起，也可能由内部因素引起．文献［11］中提出了由外部原因(如冲击)和内部原因引起的两个不同部件的冷贮备可修系统的可靠性问题，在外部的冲击流为泊松流，部件的内部寿命和修理时间遵从扩展的泊松过程的假定下，给出了该系统的系统可靠度、首次故障前平均时间、稳态可用度和稳态故障频度等可靠性指标，并研究了基于部件1的系统最优更换策略(T，N)*，其中T为部件的总使用时间，N为部件1的失效次数．

基于以上文献，文中研究了泊松冲击下的可修系统．冲击到达服从泊松过程，采用极值冲击模型．递增的几何过程是以对数方式缓慢增长，而递减的几何过程却会急剧减小，几何过程整体变化趋势比较平缓，α-幂过程则以幂级数或指数方式变化，变化趋势显著，并且α-幂过程满足中心极限定理，而几何过程不满足．因此，假设部件失效后修理时间构成递增的α-幂过程，且部件受到的冲击强度不变，其受到冲击失效后的阈值服从几何过程，通过更新报酬定理得出系统长期运行下单位时间的平均成本率函数的数学表达式，从分析方法和数值方法上证明最优更换策略的存在和唯一性．最后，通过数值例子证明文中结论的正确性，并在所有参数都给定的条件下，求出系统相应的最优更换策略．

1 模型假设

定义1 假设 ξ，η为两个随机变量，对任意实数 α，有

则称ξ随机地大于η，或者称η随机地小于ξ．

定义2 设{Xn，n=1，2，3，…}为非负独立随机变量序列，如果存在实数α，使得Xn的分布函数为Fn(t)=F(nαt)，n=1，2，…，则{Xn，n=1，2，3，…}称为α－幂过程，若EX1=λ，则

从定义2可知:

1)若 α＜0，则{Xn，n=1，2，…}是随机递增的α－幂过程;

2)若 α＞0，则{Xn，n=1，2，…}是随机递减的α－幂过程;

3)若α=0，则{Xn，n=1，2，…}为更新过程．

假设1 系统为一个部件组成的简单可修系统．开始时系统是新的，当系统失效时修理工立即修理系统．

假设2 系统从第n－1次失效维修完成到第n次失效维修完成的时间间隔为系统的第n个周期．在没受到冲击的情况下，系统从开始工作到失效的时间叫做系统的内部寿命．系统失效可能由外部冲击和内部因素两方面构成．系统不断受到冲击流的影响，冲击流为泊松流 {N(t)，t≥0}，其强度为λ＞0．系统在第n个周期内受到第j次的冲击量的大小为，j，{，j，n=1，2，…;j=1，2，…}是独立同分布的随机变量，分布函数为K(x)．系统受到冲击量为

n，j的冲击时，系统的阈值为 τn，j，当冲击量，j大于阈值 τn，j时，系统失效．对于一个固定的n，{τn，j，j=1，2，…}是独立同分布的随机变量且阈值形成一个几何过程．即记τn，j的分布函数为:

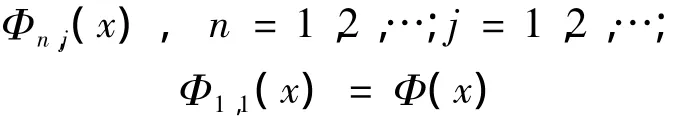
则有 Φn，j(x)=Φ(dn－1x)，n=1，2，…;j=1，2，…假设各次冲击对系统的影响是相互独立的，与冲击的历史无关．

假设3 记在第n个周期内，系统的内部寿命、工作时间、修理时间分别为Xn，Un，Yn，并且它们的分布函数分别为Ln(x)，Fn(x)，Gn(x)．

假设4 系统的失效修理是“修复非新”的，假设系统的内部寿命和修理时间均服从α－幂过程．在第n个周期内，内部寿命和修理时间均服从一般分布，即有:

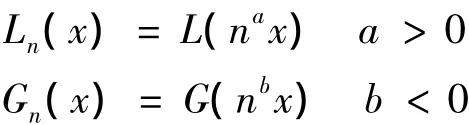
这里{Xn，n=1，2，…}是随机递减的α－幂过程，{Yn，n=1，2，…}是随机递增的 α－幂过程．记EX1=γ，EY1=μ

假设5 系统更换使用全新的同型部件，且更换时间忽略不计．

假设6 设单位时间内系统的维修费用为Cr，工作报酬为Cw，系统更换一次的费用为R0.

假设7 所有的随机变量、随机变量与冲击过程都是相互独立的.

2 最优更换策略N*

文中考虑基于系统的失效次数的更换策略N，文中的目的是找到最优更换策略N*，使得系统经长期运行的期望损失达到最小.令T1为第1次更换的周期，Tn为系统的第n－1次更换结束到第n次更换结束的时间间隔，n=2，3，….则{Tn，n=1，2，3，…}形成了一个更新过程，而相邻两次的更换时间间隔就形成一个更新周期.

基于以上假设，可以得到，在第n个周期内系统经受一次冲击引起失效的概率为:

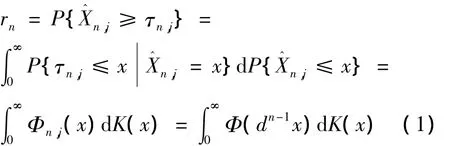
因此，每经受一次冲击不引起系统失效的概率为1－rn.

记ξn为在第n周期系统受到冲击的工作时间，则有以下引理［11－12］:

引理1 若ξn的分布函数为Vn(x)，则C(N)表示更换策略N下的系统经长期运行单位时间内的平均损失.因此，由文献［13］中的更新报酬理论可得:

由假设3，系统的工作时间为Un=min{Xn，ξn}，由于在同一周期n内，系统的内部寿命Xn与系统受到冲击的工作时间ξn是互不干扰的，所以Xn与ξn是相互独立的.因此Un的分布函数为:

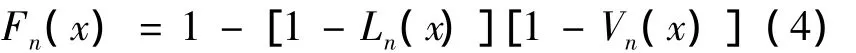
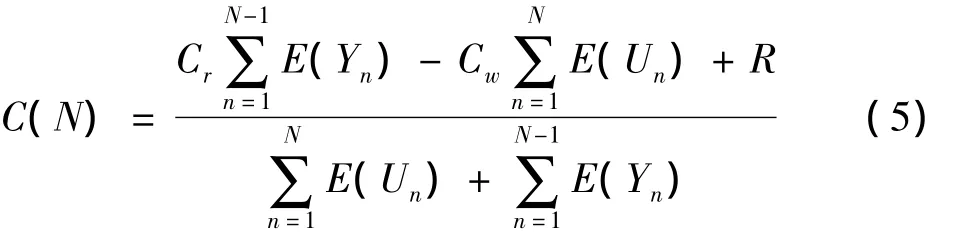
其中，

将式(6，7)代入式(5)，可得

式中:

文中目的是找到最优更换策略N*，使得系统的平均费用率C(N)或A(N)最小.因此，需要研究A(N+1)与A(N)的单调性.

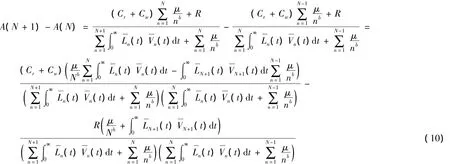
这里作一个辅助函数g(N):

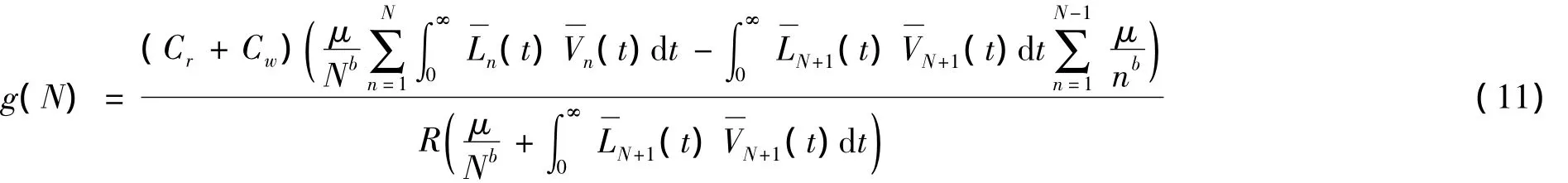
由于A(N+1)－A(N)的分母符号总大于0，则A(N+1)－A(N)的符号就取决于分子的符号，因此有以下引理2.

引理2A(N+1)＞(=，＜)A(N)⇔g(N)＞(=，＜)1.

引理2表示A(N)的单调取决于g(N)的值.下面来证明最优更换策略的存在性和唯一性.

3 最优更换策略的存在性和唯一性

为了找到最优更换策略，先研究g(N+1)－g(N)的值.令，则有

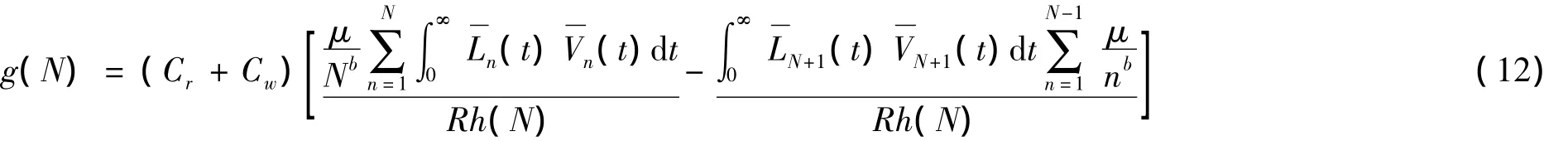
则g(N+1)－g(N)的值为:

从而得到以下定理和引理.

引理3 根据假设4，g(N)是随N单调递增的.

定理1 最优更换策略N*为:

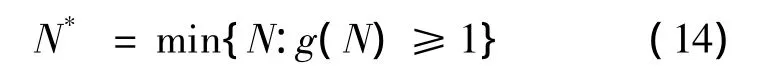
这就证明了最优更换策略的存在性.进一步，若g(N*)＞1，则最优更换策略也是唯一的.

为了根据定理1找到最优更换策略，有以下3种情况:

1)若g(1)＞1，那么最优更换策略是当部件第1次失效时立即更换新部件.

3)由定理2，可以找到最优更换策略，从N=1开始计算g(N)的值，因为引理3证明了g(N)是递增的，那么存在一个N*，并且N＜N*⇔g(N)＜1，所以由定理2和引理3可知N*是最优更换策略.

4 数值模拟

将给出一个数值例子来证明模型的理论结果.假设冲击X^1和阈值τ1，1的分布函数如下:

由前面假设2可知Φn，j(x)=Φ(dn－1x)，于是可得出

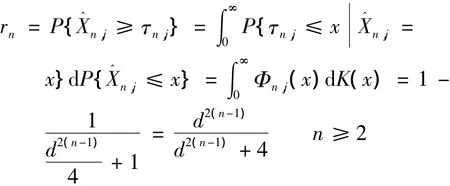
假设Xn和Yn的分布函数分别为:

代入式(4)，则系统的工作时间为:

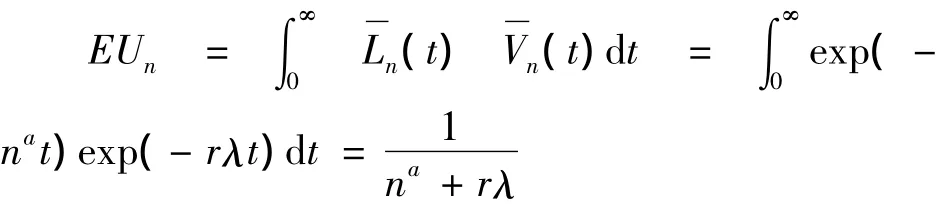
则系统经长期运行，平均费用率C(N)和g(N)表达式为:模型参数分别设为:

a=0.2，b=－0.98，d=1.15，μ=0.2，

λ=0.5，Cr=4，Cw=34，R=100将参数值代入式(15，16)，通过Matlab计算，结果如图1，2和表1所示.

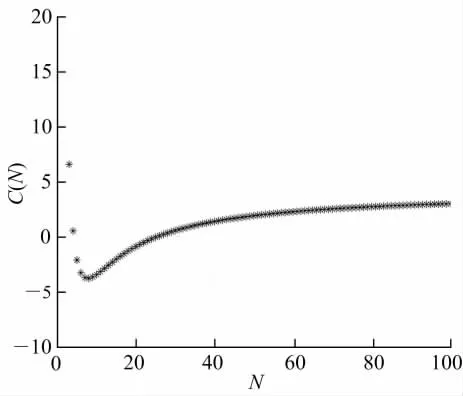
图1 更换策略N和平均损失的关系Fig.1 Relation between replacement policy Nand the average cost

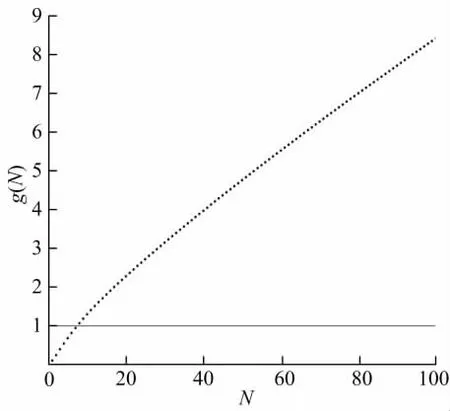
图2 更换策略N和g(N)的关系Fig.2 Relation between g(N)and replacement policy N

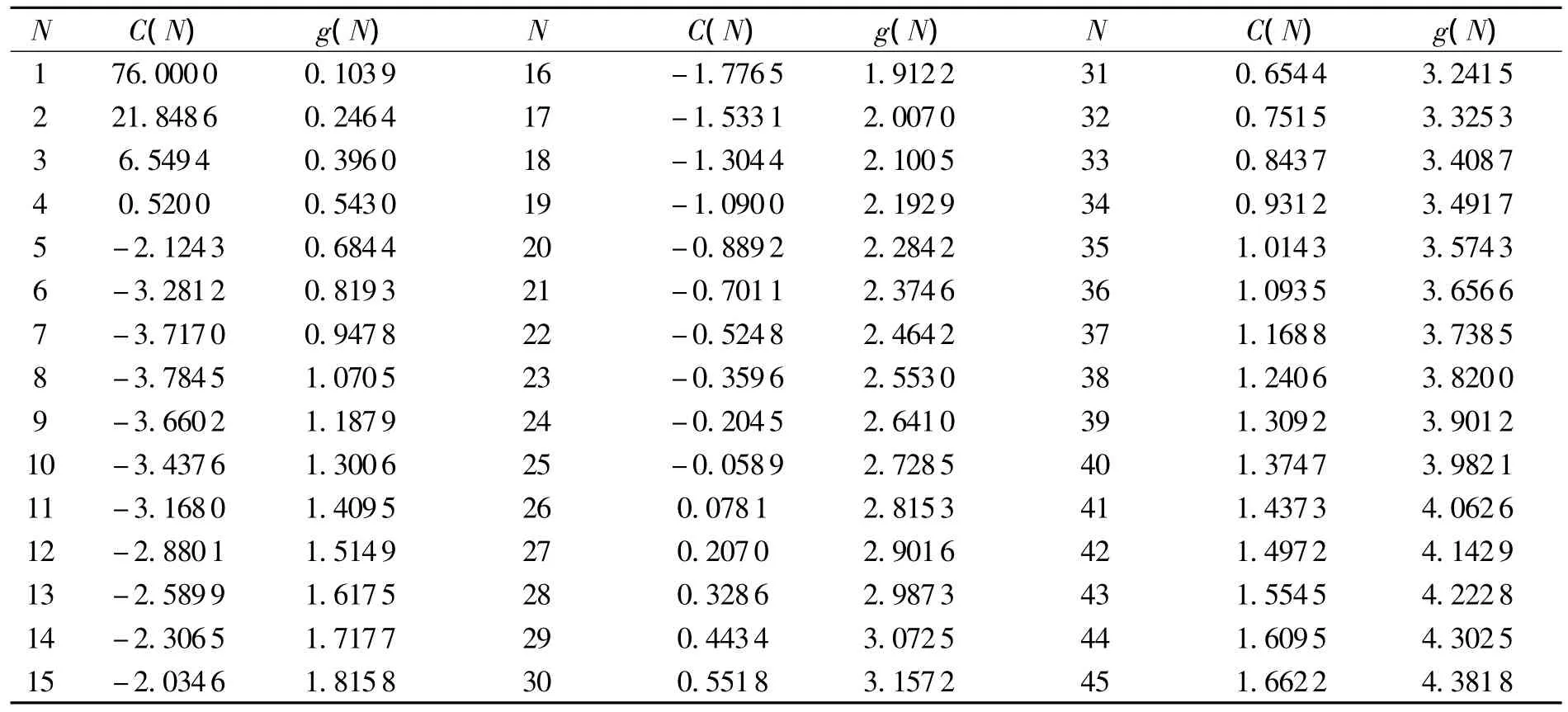
表1 更换策略N与g(N)，C(N)之间的关系数值Table 1 Values of C(N)and g(N)against replacement times N

由图1和表1可知，当N≤8，系统失效由受外部冲击和内部因素引起时，系统经长期运行，单位时间内的平均损失C(N)随N单调递减，当N＞8时，C(N)随N单调递增.则使得系统经长期运行的平均费用率最小的最优更换策略为N*=8，此时C(N)=－3.7845为系统最小平均费用率.由图2可得，g(N)随N单调递增，这就暗示了最优更换策略的存在性和唯一性，验证了文中第3节的理论.并且也可以由g(N*)=g(8)=1.0705找到最优更换策略N*=8，与之前相一致.这表示系统在第8次失效时就应该更换系统了.

5 结论

文中研究了泊松冲击下的单部件可修系统.系统失效可能由外部冲击和内部原因引起，冲击到达服从泊松过程.在假定系统阈值呈现几何过程和修理过程为α-幂过程的基础上，通过更新报酬定理求出系统长期运行下单位时间的平均成本率函数的数学表达式，从分析方法和数值方法上证明最优更换策略的存在和唯一性;最后，通过数值例子证明文中导出的结论的正确性，并在所有参数都给定的条件下找出系统的最优更换策略，验证了文中的结论.

References)

［1］ Yeh L.A note on the optimal replacement problem［J］.Advances in Applied Probability，1988，20:479-482.

［2］ Yeh L.Geometric processes and replacement problem［J］.Acta Math Appl Sinica，1988，4:366-377.

［3］ Yeh L.A repair replacement model［J］.Advances in Applied Probability，1990，22:494-497.

［4］ Stadje W.Zuckerman D.Optimal strategies for some repair replacement models［J］.Advances in Applied Probability，1990，22:641-656.

［5］ Jia Jishen，Liu Sifeng，Dang Yaoguo.Study on the optimal replacement policy for a deteriarative repairable system ［J］.System Engineering-Theory MethodologyApplications，2006，28(1):80-82.

［6］ Wang H.A survey of maintenance policies of deteriorating systems［J］.European Journal of Operational Research，2002，139(3):469-489.

［7］ Braun W J，Li W，Zhao Y Q.Properties of the geometric and related processes［J］.Naval Research Logistics，2005，52(7):607-616.

［8］ 周玉霞.退化系统的α-幂过程维修模型的最优更换策略的单调性［J］.四川大学学报:自然科学版，2007，44(2):221-224.Zhou Yuxia.Monotonicity of the optimal replacement policy for the α-power process maintenance model［J］.Journal of Sichuan University:Natural Science E-dition，2007，44(2):221-224.(in Chinese)

［9］ 唐亚勇，刘亚萍.退化系统的α-幂过程维修模型［J］.四川大学学报:自然科学版，2007，44(3):503-507.Tang Yayong，Liu Yaping.An α-power process maintenance model for a deteriorating system ［J］.Journal of Sichuan University:Natural Science Edition，2007，44(3):503-507.(in Chinese)

［10］ 吴清太，唐加山.泊松冲击下冷贮备可修系统的可靠性分析［J］.数理统计与管理，2012(1):149-156.Wu Qingtai，Tang Jiashan.Reliability analysis for cold standby repair system under poisson shock［J］.Journal of Applied Statistics and Management，2012(1):149-156.(in Chinese)

［11］ Wu Qingtai，Wu Shaomin.Reliability analysis of twounit cold standby repairable systems under Poisson shocks［J］.Appl Math Comput，2011，218(1):171-182.

［12］ Shanthikumar J G，Sumita U.Distribution properties of the system failure time in a general shock model［J］.Advances in Applied Probability，1984，16:363-377.

［13］ Ross S M.Stochastic processes［M］.2rd Edition.New York:Wiley，1996:89-91.