囊式空气弹簧静态特性计算方法

赵应龙，何 琳，吕志强

(1.海军工程大学振动与噪声研究所，湖北武汉 430033;2.船舶振动噪声重点实验室，湖北武汉 430033）

囊式空气弹簧静态特性计算方法

赵应龙1，2，何 琳1，2，吕志强1，2

(1.海军工程大学振动与噪声研究所，湖北武汉 430033;2.船舶振动噪声重点实验室，湖北武汉 430033）

囊式空气弹簧是一种承载和刚度均可调的隔振元件，其承载和刚度特性不仅取决于气压，还与其几何形状和壳体材料性质有关。船舶隔振装置的设计和应用需要确定空气弹簧在不同高度和不同气压下的承载能力和刚度大小，但其在任意状态下有效面积和刚度的全部数据无法依靠实验测量获得，针对囊式空气弹簧在不同状态下有效面积的难以试验测试确定的特点，基于弹性薄壳无矩理论，给出一种船用囊式空气弹簧静态特性的计算方法，推导承载力和静刚度的计算公式，并通过算例验证该方法的计算过程，为船用空气弹簧的设计和应用提供理论依据。

空气弹簧;刚度;有效面积;薄壳;囊式

0 引言

空气弹簧最早应用于铁道车辆。美国自1947年在普尔曼车上首次使用，而后意大利、英国、法国等许多欧洲国家对其进行了大量研究。1955年，日本国家铁路技术研究院机车车辆动力实验室对用于车辆的空气弹簧进行了系统研究，还对装有空气弹簧的车辆进行了一系列的试验工作［1－2］。在军事领域，俄罗斯已在其常规潜艇上大量应用空气弹簧［3］。

国内外大量文献报道了空气弹簧静态特性的研究进展，这些文献主要基于气体状态方程推导出空气弹簧刚度表达式，将刚度表示为压力、有效面积及其偏导数所构成的公式［4－6］。

文献［7－10］介绍了采用非线性有限元分析技术研究空气弹簧的方法，其中橡胶囊的模型均采用层状复合材料结构的壳单元结构，主方向的弹性模量采用复合材料微观力学的方法近似计算求得，这样定义的层状复合材料通过设定材料的主方向、各铺层厚度和铺设角度来确定材料的构成关系，只能获得平均效应，没有准确的模拟空气弹簧的材料特性。

当盖板直径小于或等于经线方向剖面的圆弧曲率中心距离时，囊式空气弹簧有效面积的计算是容易的，而此种空气弹簧囊体却很难达到很高的强度，因而承受的气压通常在1 MPa以下，而且体积相对较大，也很难在有空间尺寸要求、承载却相对较大的地方使用。也有文献［11］对盖板直径大于经线方向剖面的圆弧曲率中心距离的囊式空气弹簧的承载力进行计算。在考虑囊体的平衡时，将气体压力在囊体外水平方向上的合力与囊体内力在囊体内水平方向上的合力视作相等，从而计算出囊体内力等于压力与经线方向剖面圆弧半径的乘积，这一假设的理论依据不充分。

船舶动力装置隔振所使用的囊式空气弹簧一般要求体积小、承载大，从而空气弹簧工作气压高;囊体的强度大，囊体的安全系数高。这些因素决定了船舶动力装置隔振用囊式空气弹簧的盖板直径一般设计成大于其经线方向剖面圆弧曲率中心距离。另一方面，空气弹簧隔振装置的静平衡是超静定的，需要通过调整空气压力分布来调整装置的平衡姿态，这就需要确定囊式空气弹簧在不同承载、不同高度、不同压力时的有效面积。因此，完全依靠实验来确定其不同状态时有效面积以实现控制不现实。本文正是针对这一情况，基于弹性壳体理论，提出一种船用囊式空气弹簧承载力及其静刚度的计算方法，为船用空气弹簧的设计和应用提供理论依据。

1 理论依据

本文研究的空气弹簧是单曲圆弧回转体囊，并且上下对称，计算模型如图1所示。由于空气弹簧所受的边界条件和载荷都是绕回转轴对称的，并且囊体较薄，其几何和材料特性符合弹性薄壳理论中的假定。可根据回转薄壳的无矩理论建立空气弹簧囊体的平衡方程和物理方程，具体的回转薄壳无矩理论参见文献 ［12］。

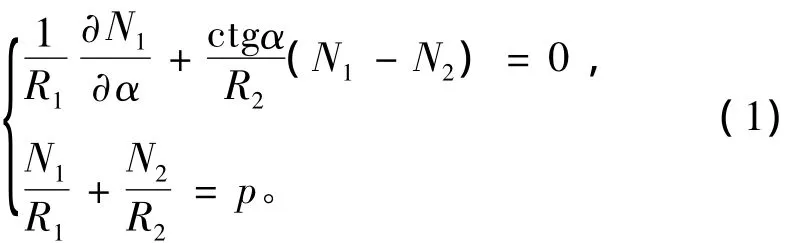
囊体平衡方程为:式中:α为经线坐标，即囊体外法线方向与轴线上方向夹角;R1和R2分别为经线和纬线的拉密系数，即弧半径和囊体法线被轴线所截距离;N1和N2分别为经线和纬线方向的内力;p为囊体所受静压力。

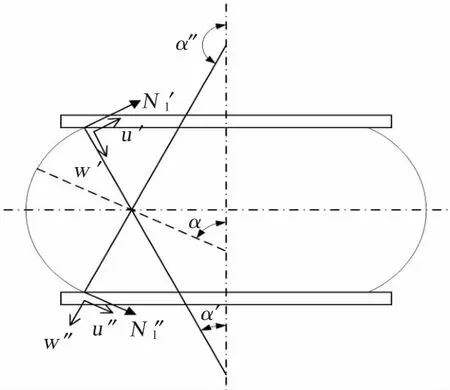
图1 囊式空气弹簧计算模型Fig.1 Calculatingmodel of bellows type air spring

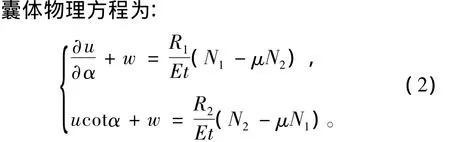
式中，u和w为囊体经线方向和法线方向位移;E和μ为囊体材料弹性模量和泊松比;t为壳体厚度。

设空气弹簧承载为G，则由式(1）可得:

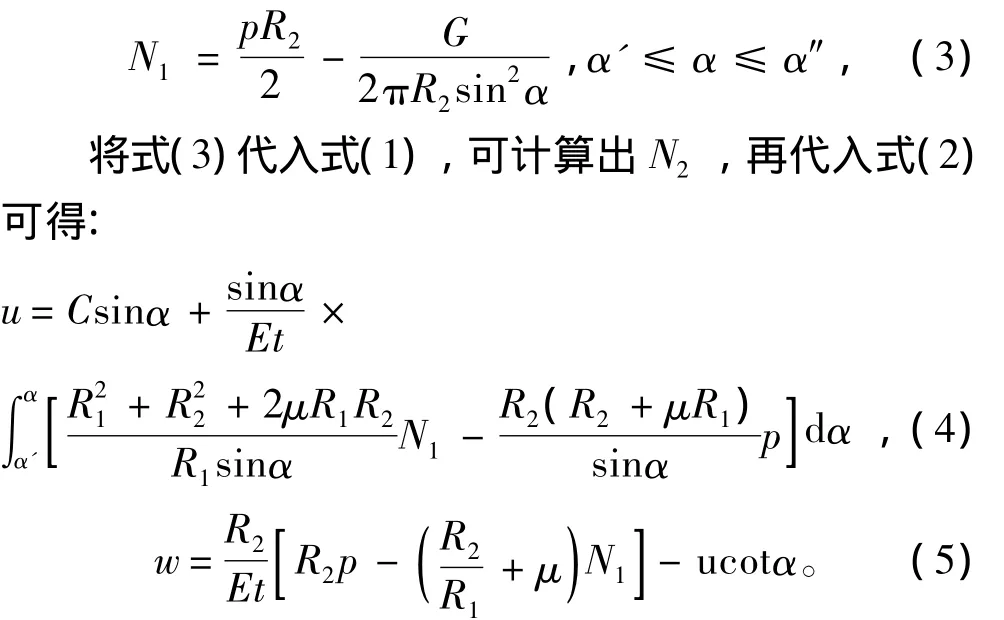
式中C为常数，由边界条件确定。

囊体在各种静平衡状态下的受力和变形都可用上述内力和位移公式求解。为确定边界条件及计算参数的选取，现将几种平衡状态规定如下:

1）囊体不受任何气体压力和外界力，囊体处于“自然”状态时称为状态①。

2）状态①中囊体不受气体压力，仅受到垂向的拉力或压力并处于某一高度达到平衡时称为状态②。

3）向状态②囊内充气或向囊体加载代替状态②中的拉力或压力，囊体保持状态②中相同的几何形状而处于平衡称为状态③。

4）保持状态③中囊体高度不变，但调整压力和载荷，囊体处于新的平衡称为状态④。

5）将状态③或状态④中囊体拉伸或压缩到某一高度后的平衡称为状态⑤。

2 承载力计算

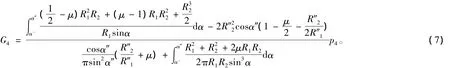
空气弹簧承载力的计算，就是计算由状态③变化到状态④空气弹簧承载与压力之间的函数关系。在变化过程中，囊体高度始终保持不变，因此有如下边界条件:

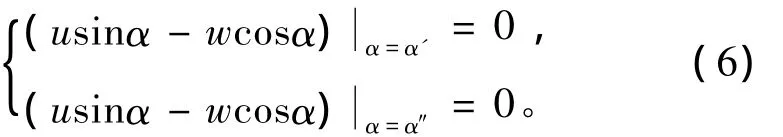
式中α'和α″分别为囊体上下边界的α坐标值。将式(3）～式(5）代入式(6），并注意到α″=π－α'得:

式中:G4为状态④时承载力计算公式;α'，α″，R'1，R″1，R'2，R″2为空气弹簧状态③时的值;p4为状态④时气压;G4与p4之比称为有效面积。

3 静刚度计算

空气弹簧静刚度的计算，就是计算由状态③变化到状态⑤，或状态④变化到状态⑤所施加的外力与空气弹簧位移的比值;状态③变化到状态⑤的静刚度和状态④变化到状态⑤的静刚度是不同载荷所对应的静刚度。本文以计算状态④变化到状态⑤的静刚度为例，在变化过程中，囊体下边界固定不动，上边界沿垂直方向运动，因此有如下边界条件:

式中h4和h5分别为状态④、⑤时的囊体高度。由此可见，不同承载、不同位移产生的静刚度也不同，并且静刚度和初始气压成正比，其比值称为形状系数。

4 算例分析

对于船舶动力装置使用的囊式空气弹簧，由于囊体强度要求高，在变形过程中可认为母线长度l基本不变，以下计算都是在这一条件下进行的。设l=105 mm;囊体上边界半径，即 R'2sinα'=180 mm;μ=0.01;就可以得到有效面积随囊体高度变化曲线 (见图2）。由于母线长度保持不变且由状态③变化到状态④囊体高度也未发生变化，则状态③与状态④的囊体形状是相同的，这样就可以得到不同高度、不同拉压位移时的静刚度形状系数表 (见表1），表中单位N/mm/MPa，列为变形前α'值，行为变形后α'值，表中左下角为空气弹簧压缩时静刚度形状系数，右上角为空气弹簧拉伸时竟刚度形状系数。

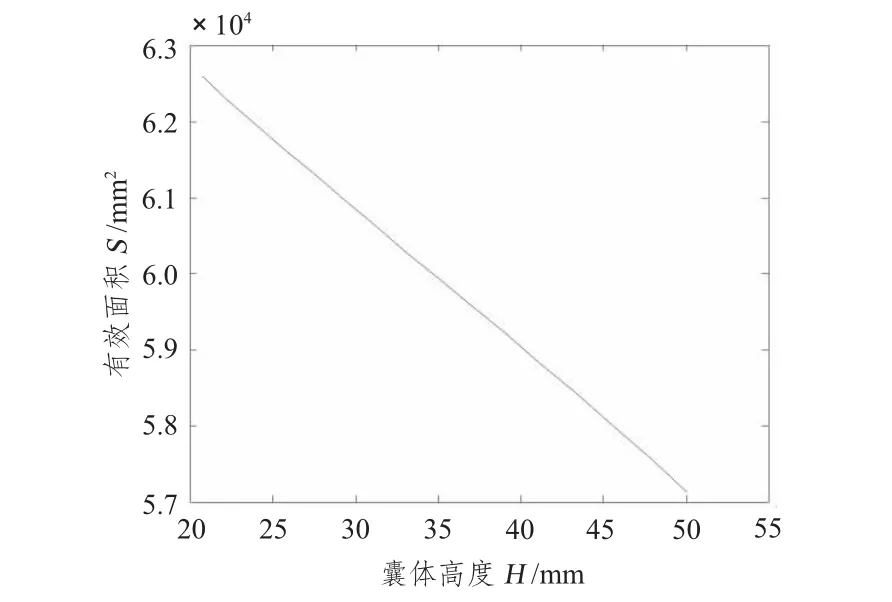
图2 有效面积随囊体高度变化图Fig.2 Curve of effective area vs.height of air spring

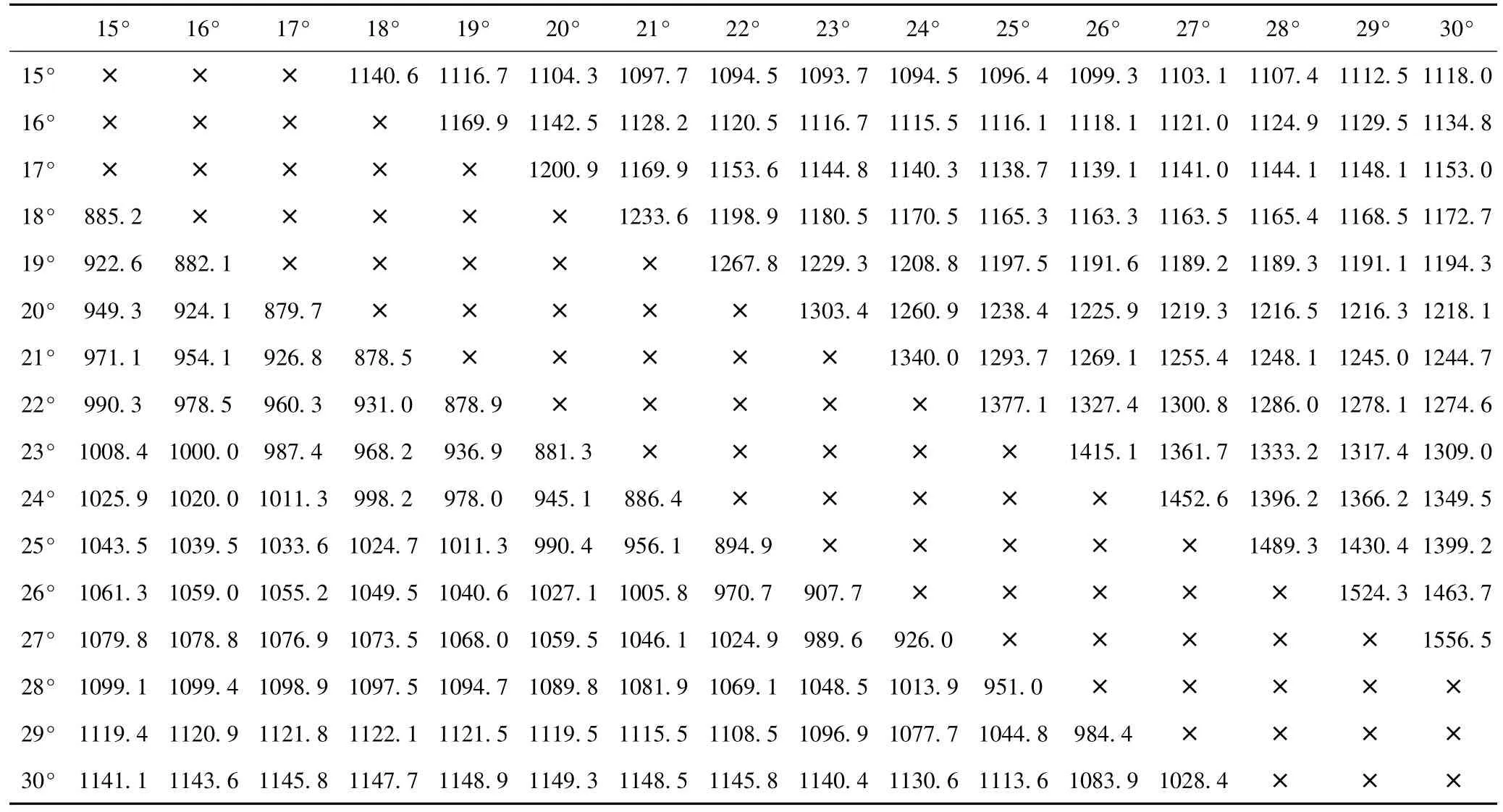
表1 静刚度形状系数Tab.1 Cefficient related to shape of air spring for static stiffness

5 结语

算例分析表明，空气弹簧的有效面积随囊体高度变化而变化，其变化基本是线性的;高度越大，有效面积越小，反之则越大。图中数据显示，如果高度变化极小，则有效面积的变化可忽略不计，因此小振幅振动有效面积可认为不变化。另一方面，对于相同的载荷，空气弹簧可以在不同高度平衡，但不同高度所对应的气压不同，高度越大，气压越大，反之越小，空气弹簧可以调节气压来适应不同的高度。还需指出的是，空气弹簧的静刚度计算极其复杂，但其主要取决于囊体几何形状的变化。从表中数据看出，不同囊体形状变化过程产生的平均静刚度变化可以超过60%，因此空气弹簧作为隔振使用时应工作在某一形状范围内，否则其性能难以控制。

综上所述，本文提出的船用囊式空气弹簧承载力及其静刚度的计算方法，为船用空气弹簧的设计和应用提供了理论依据。

［1］赵雅.空气弹簧在高速客车转向架上的应用［J］.上海铁道大学学报，2000，21(4）:91 －93.

［2］林通雄［日］.车辆用空气弹簧［J］.国外铁道车辆，1990(2）:16－18:91－93.

［3］叶珍霞.高内压大载荷空气弹簧非线性有限元法优化设计［D］.武汉:海军工程大学，2005.

［4］朱石坚，黄映云，何琳，等.长方体形囊式空气弹簧刚度特性研究［J］.非线性动力学学报，2001，8(1）:39 －46.

［5］张利国，张嘉钟，贾力萍，等.空气弹簧的现状及其发展［J］.振动与冲击，2007，26(2）:147 －151.

［6］黄映云，吴善跃，朱石坚.囊式空气弹簧隔振器的特性计算研究［J］.振动工程学报，2004，17(2）:249 －252.

［7］张广世.有限元法研究空气弹簧参数对横向特性的影响［J］.铁道车辆，2000(9）:13 －16.

［8］方凯.一种新型高速客车空气弹簧的非线性有限元分析［J］.铁道机车车辆，2001(6）:8 －10.

［9］ERIN C，WILSON B，ZAPFE J.An improved model of pneumatic vibration isolator theory and experiment［J］.Journal of Automobile Engineering，Proc Instn Meah Engrs，1995(209）:227 －234.

［10］KAYSUYA T.Study on dynamic characteristic analysis of air spring with auxiliary chamber［J］.JSAE Review，1999(3）:349－355.

［11］罗贤光.曲囊式橡胶空气弹簧的一些力学问题［J］.橡胶工业，1997，44(4）:228 －232.

［12］徐芝纶.弹性力学［M］.北京:高等教育出版社，1990.

A static characteristics calculation method for bellows type air spring

ZHAO Ying-long1，2，HE Lin1，2，LV Zhi-qiang1，2
(1.Institute of Noise and Vibration，Naval University of Engineering，Wuhan 430033，China;2.National Key Laboratory on Ship Vibration and Noise，Wuhan 430033，China）

Bellows type air spring is a kind of vibration isolator whose load-bearing and stiffness both can be adjusted.Its characteristics of load-bearing and stiffness depend notonly on air pressure，butalso on its geometry and shell material property.Ship vibration isolating sets design and application require the knowledge of load-bearing ability and stiffness of the spring under various altitude and air pressure.However all the data of its effective area and stiffness can not be achieved on the experiment.According to elastic thin shell theory，a static characteristics calculation method for bellows type air spring for ship is presented in this paper.Then，the calculating formula of air spring bearing capacity and static stiffness is deduced，and an illustrative instance is given to explain the calculation process of themethod.Thus itmay provide a theoretical evidence for designing and application on bellows type air spring.

air spring;stiffness;effective area;thin shell;bellows type

O328，0241

A

1672－7649(2014）05－0097－04

10.3404/j.issn.1672－7649.2014.05.020

2013－04－22;

2013－06－27

总装“十一五”预研计划资助项目

赵应龙(1976－），男，博士，从事舰船设备减振降噪及抗冲击技术研究。