航行器水中运动数学模型及数值仿真
齐 强,陈志刚,周 源
(1.海军航空工程学院飞行器工程系,山东烟台 264001;2.海军航空工程学院战略工程导弹系,山东烟台 264001)
航行器水中运动数学模型及数值仿真
齐 强1,陈志刚1,周 源2
(1.海军航空工程学院飞行器工程系,山东烟台 264001;2.海军航空工程学院战略工程导弹系,山东烟台 264001)
根据水下垂直发射航行器水中运动的特点,利用质心运动定理和绕质心的动量矩定理,推导建立航行器水中运动的运动学模型和动力学模型。采用Matlab软件中的ODE解算器,对建立的数学模型进行数值仿真,得到航行器水中运动的速度和姿态角。
水下垂直发射;数学模型;ODE解算器;数值仿真
0 引言
水下垂直发射的航行器,从发射筒中被弹射出去之后,要经过水下航行器所特有的水中弹道。虽然航行器在水中的行程很短,只占全弹道很小的一部分,但由于水中力学环境复杂,它的设计和研究在水中航行器研制过程中占有很重要的地位。水中弹道设计计算的准确性直接影响到整个航行器系统的性能[1-2]。
无控航行器可以近似地看作自由刚体,在水中做六自由度运动,即质心的运动和绕质心的运动[3]。在不考虑发射海情的条件下,对水中运动的航行器进行受力分析,并通过质心运动定理和相对于质心的动量矩定理,建立航行器的运动学模型和动力学模型,确定航行器的6个自由度的运动,从而确定航行器在空间的任一瞬时的位置和姿态。
1 坐标系的建立
根据航行器水中运动模型的需要,文中建立发射坐标系、弹体坐标系和速度坐标系3个右手坐标系 (见图1)。
发射坐标系原点o位于脱离发射筒时航行器浮心对应的位置,ox轴指向发射方向,oy轴铅垂向上。
弹体坐标系原点o1位于航行器浮心,o1x1轴与航行器纵轴重合指向航行器头部,o1y1轴居于纵对称面,指向上方。
速度坐标系原点o1位于航行器浮心,o1xv轴始终与航行器的速度矢量方向重合,o1yv轴在航行器的纵对称面,指向上方。
设发射坐标系到弹体坐标系的转换矩阵为Az-z1,且

图1 坐标系示意图Fig.1 Diagram of coordinate system

2 航行器水中运动的受力分析
2.1 作用在航行器上的力和力矩
1)流体动力和流体动力矩
航行器在水中运动时受到流体动力和流体动力矩的作用,流体动力和流体动力矩的大小取决于流体介质的性质、航行器外形以及航行器的运动状态[4-5]。将流体动力和流体动力矩分解到弹体坐标系,有:
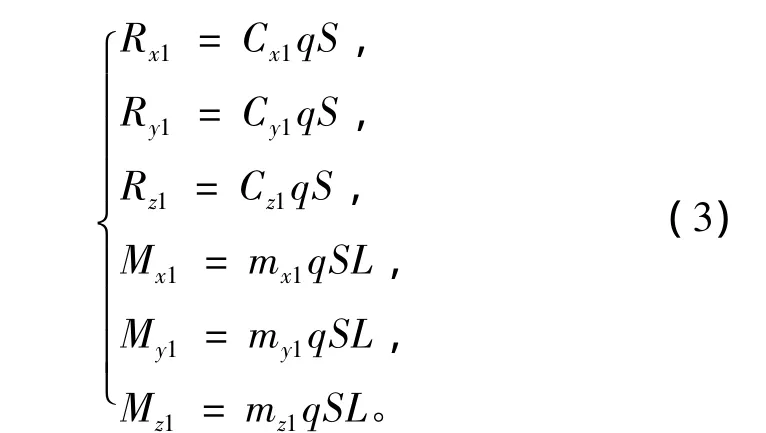
式中:Cx1,Cy1和Cz1为流体动力因数;mx1,my1和mz1为流体动力矩因数;q为流体动压力;S为航行器的最大横截面积;L为航行器的长度。
2)重力
航行器所受到的重力为

其中m为航行器的质量。
重力铅垂向下,沿着发射坐标系oy轴负向,其在弹体坐标系中的3个分量为

航行器的浮心和重心不重合。设航行器重心在航行器的纵对称轴上,且与航行器浮心之间的距离为lB,则航行器的重力矩MG在弹体坐标系中的分量为
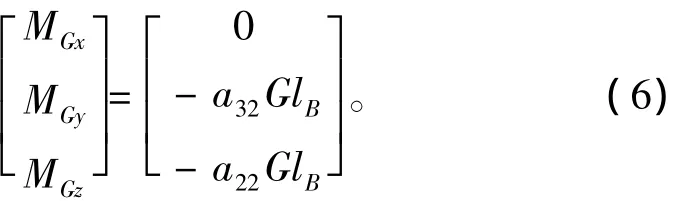
3)浮力
航行器在水中运动时所受到的浮力大小为

式中:ρ为海水密度;V为航行器体积。
浮力是铅垂向上的力,方向沿发射坐标系oy轴,在弹体坐标系中的分量为

2.2 航行器的附加惯性质量
航行器所受的流体惯性力和惯性力矩根据理想流体惯性力计算,表现为航行器运动的附加质量和附加转动惯量[4,6]。在选定坐标系后,航行器的附加质量仅与导弹的外形有关。在弹体坐标系中,航行器的附加质量矩阵为

3 航行器运动学方程和动力学方程
3.1 运动学方程
1)航行器的质心运动
以发射坐标系作为惯性参考系,在惯性参考系内,假设航行器质心的坐标为(x,y,z),那么航行器在发射坐标系中的速度为(˙x,˙y,˙z)。
设航行器的速度在弹体坐标系中的投影为(vx1,vy1,vz1),根据弹体坐标系到发射坐标系的转换关系,得到

2)航行器绕质心的运动
设航行器的姿态角 (欧拉角)在发射坐标系中的分量分别为俯仰角θ、偏航角φ和滚转角γ,那么航行器的欧拉角角速度为(˙θ,˙φ,˙γ)。
设航行器的角速度ω在弹体坐标系中的投影为(ωx1,ωy1,ωz1),根据坐标转换关系,有
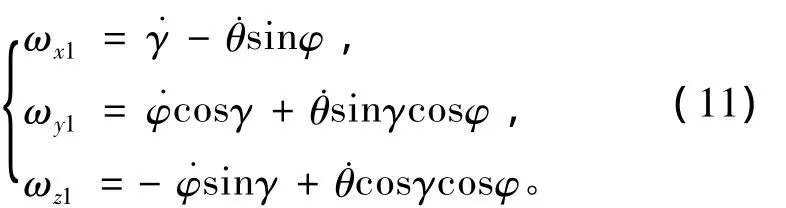
3.2 动力学方程
根据动量定理和动量矩定理,航行器的动力学方程[3,5,7 -8]为
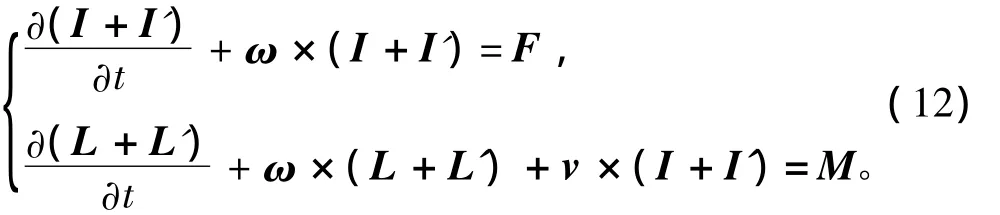
式中:I和I'分别为航行体和航行体周围流体的动量矢量;L和L'分别为航行体和航行体周围流体的动量矩矢量;ω为航行体的角速度矢量;v为航行体的速度矢量;F为航行体所受到的外力矢量之和;M为航行体所受到的外力矩矢量之和。
将式(3)~式(8)代入式(12)可以得到航行器水中运动的动力学方程组(13)和(14)。

4 算例
对于航行器水中运动模型,采用4阶5级Runge-Kutta法[9]进行数值求解,可以保证数值解的高精度和稳定性。由于Matlab软件中的ODE解算器可以快速精确地计算常微分方程组,所以本文在Matlab环境中对航行器的运动学和动力学方程组进行求解。
计算中取航行器的质量m=40 t,直径D=2 m,长度L=12 m,发射深度H=28 m。
航行器水中运动的速度和姿态角的仿真曲线如图2~图5所示。

图2 速度-时间曲线Fig.2 Velocity-time curve

图3 姿态角-时间曲线Fig.3 Angle of attitude-time curve
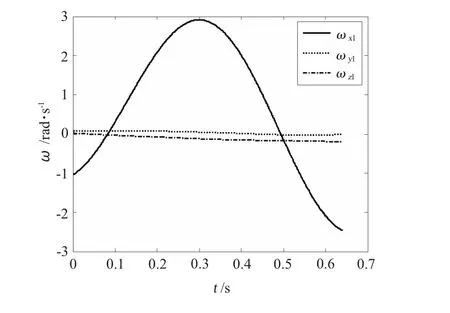
图4 角速度-时间曲线Fig.4 Angular velocity-time curve
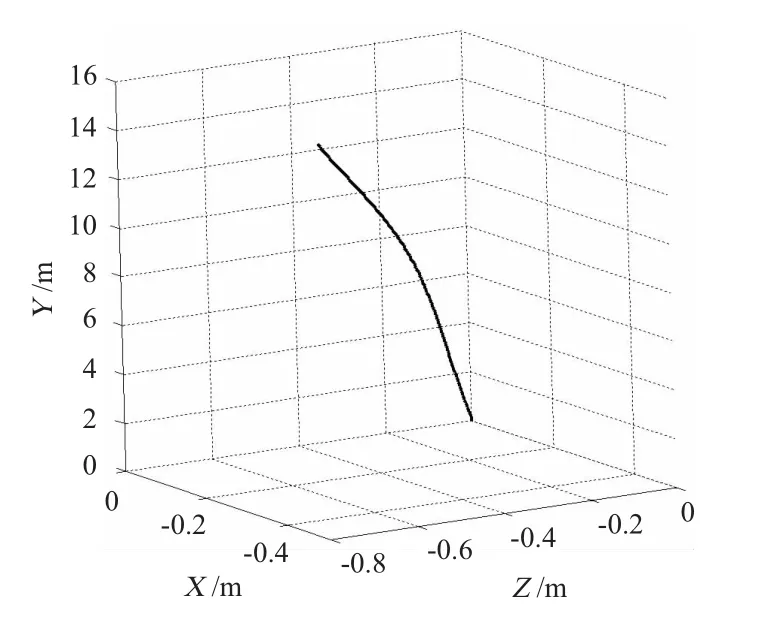
图5 航行器质心空间位置曲线Fig.5 Diagram of centroid
航行器从离开发射筒到头部出水之间的时间为0.64 s。航行器在头部出水之前的速度为18.792m/s,俯仰角为85.425 7°。
航行器从发射筒中垂直发射出去之后,受到水动力的作用,航行器的速度、角速度和姿态角发生,特别是航行器的轴向速度和滚转运动呈现急剧的变化。航行器的水中运动是加速度逐渐减小的减速过程。航行器运动速度大时加速度大,速度减小时加速度减小。
5 结语
本文建立的动力学模型和运动学模型可以很好地体现航行器的水中运动规律,所采用的数值计算方法快速准确地计算出了航行器的水中弹道,为航行器发射内弹道和出水弹道计算提供理论参考。
[1]李延军,郭凤美,董利强.水下飞行器的弹道仿真[J].导弹与航天运载学报,2009(6):1-4.
LI Yan-jun,GUO Feng-mei,DONG Li-qiang.Trajectory simulation of underwater vehicle[J].Missile and Space Vehicles,2009(6):1 -4.
[2]王聪,王学孝,徐世昌,等.潜射导弹运动特性分析与测试[J].战术导弹技术,2002(2):9-12.
WANG Cong,WANG Xue-xiao,XU Shi-chang,et al.Analysis and testing on dynamic characteristics of submarine launched missile[J].Tactical Missile Technology,2002(2):9 -12.
[3]宗瑞良,陈连平,蒋小奎.火箭航行器水中运动数学模型[J].西北工业大学学报,2000,18(2):254 -258.
ZONG Rui-liang,CHEN Lian-ping,JIANG Xiao-kui.A mathematical model for underwater rocket motion[J].Journal of Northwestern Polytechnical University,2000,18(2):254-258.
[4]黄寿康.流体动力·弹道·载荷·环境[M].北京:宇航出版社,1991:406-415.
HUANG Shou-kang.Fluid,ballistic,load,environment[M].Beijing:Astronautics Press,1991:406 -415.
[5]严卫生.鱼雷航行力学[M].西安:西北工业大学出版社,2005:106-115.
YAN Wei-sheng.The torpedo sailing mechanics[M].Xi'an:Northwestern Polytechnical University Press,2005:106-115.
[6]仲维国,张嘉钟.潜射航行器的水下弹道模拟[J].弹道学报,2005,17(1):8 -12.
ZHONGWei-guo,ZHANG Jia-zhong.Numerical simulation of underwater-launched vessel's submarine trajectory[J].Journal of Ballistics,2005,17(1):8 -12.
[7]方宁,宋召青.潜载垂直发射导弹水下弹道建模与仿真[J].海军航空工程学院学报,2010,25(3):311 -314.
FANG Ning,SONG Zhao-qing.Model and simulation for the underwater trajectory of submarine-based vertical-launched missile[J].Journal of Naval Aeronautical and Astronautical University,2010,25(3):311 -314.
[8]张永,刘曜,胡德斌.基于MATLAB的潜空导弹运载器的水弹道研究[J].战术导弹技术,2007(5):7-10.
ZHANG Yong,LIU Yao,HU De-bin.Research on capsule's trajectory of submarine launched missile based on matlab[J].Tactical Missile Technology,2007(5):7 -10.
[9]薛定宇,陈阳泉.高等应用数学问题的 Matlab求解[M].北京:清华大学出版社,2004:209-217.
XUE Ding-yu,CHENG Yang-quan.The Matlab solving of advanced applied mathematics problem[M].Beijing:Tsinghua University Press,2004:209 -217.
Mathematicalmodel and simulation for underwater motion of vehicle
QIQiang1,CHEN Zhi-gang1,ZHOU Yuan2
(1.Naval Aeronautical Engineering Institute,Department of Airborne Vehicle Engineering,Yantai264001,China;2.Naval Aeronautical Engineering Institute,Department of Strategic Missile Engineering,Yantai264001,China)
Based on features of vertical launching underwater,the kinematics model and dynamics model for underwater motion of vehicle were established by the theorem of centroid movement and the moment theorem.Themathematicalmodelwas simulated numericallywith the ODE solver ofMatlab.And the resultwas the velocity and attitude angle of vehicle in the underwatermotion.
vertical launching underwater;mathematicalmodel;ODE solver;numerical simulation
TJ02
A
1672-7649(2014)05-0080-04
10.3404/j.issn.1672-7649.2014.05.016
2013-04-09;
2013-05-06
齐强(1965-),男,博士,副教授,主要研究方向为发射工程。

