滚动轴承寿命计算方法发展的研究与分析
朱亮亮,林素敏,吉晓民
(1.杨凌职业技术学院,陕西 咸阳 712100;2. 西安理工大学,陕西 西安 710054)
滚动轴承寿命计算方法发展的研究与分析
朱亮亮1,林素敏1,吉晓民2
(1.杨凌职业技术学院,陕西 咸阳 712100;2. 西安理工大学,陕西 西安 710054)
详细介绍了滚动轴承疲劳寿命的概念,并对滚动轴承疲劳寿命的发展历程进行了详细阐述,分析了各个不同时期寿命计算理论的特点,谨供相关人士参考。
滚动轴承;疲劳寿命;剪切应力;疲劳剥落
1 前言
滚动轴承是一种精密的机械基础件,具有通用性、标准化、系列化特点;同时滚动轴承也是机械设备中重要的易损部件之一。统计表明,在使用滚动轴承的旋转机械中,大约30%的机械故障是由滚动轴承引起的。滚动轴承重要的质量指标之一就是疲劳寿命。对滚动轴承疲劳寿命的研究与分析,直接影响设备的效率和安全,具有重要意义。
2 滚动轴承的疲劳寿命
近年来,SKF等公司经过大量的研究发现,轴承的工作环境及本身的质量状态对疲劳寿命有很大影响。例如,在污染状态下,轴承润滑剂中混有固态异物,将大大降低轴承寿命;润滑剂油膜的厚度,对轴承寿命也有较大影响;轴承组件的表面粗糙度对轴承寿命也有影响。减少、减弱有关因素对寿命的影响程度,提高寿命预测准确度,是延长轴承疲劳寿命的有效途径[1]。
轴承带载工作时,负荷从外(内)圈通过滚动体传到内(外)圈,此时,在滚动体与内外滚道接触表面的金属材料之下,就会出现最大的剪切应力。当滚动体滚过滚道,即轴承旋转一周,这个剪切应力就会反复循环出现。当循环次数达到一定值时,金属便会出现疲劳,随之出现破坏失效。不论轴承是什么材质,这个剪切应力的循环一定会出现。经过研究发现,剪切应力出现的时间与大小有两个影响因素:滚动体滚过的次数和正压力,并且他们成正比例的关系。当金属表面出现第一个疲劳点后,疲劳会沿着一定的方向或顺序,在整个金属表面蔓延扩大,最终的结果是出现轴承金属的表面剥落。这种失效形式叫做表面下疲劳剥落[2],是轴承失效形式中非常典型的一种。
当轴承出现一定面积的疲劳剥落,把该疲劳剥落出现的时间或转动次数,定义为轴承疲劳寿命。但金属疲劳是通过统计学分析得到的,对于单个轴承的寿命,是不可能精确判断的。因此,目前预测轴承寿命的方法是:在同等条件下,对一组被测试轴承进行统计学评估。在任一确定的可靠度下,利用维泊尔分布函数可以来预测轴承的寿命[3]。
从普通意义上讲,轴承疲劳寿命是指轴承在一定结构、工艺状态、配合、安装、游隙和润滑等状态下,主机正常运转,直至滚动轴承表面发生疲劳破坏,而不能满足主机正常工作要求,此时轴承内、外圈(轴、座圈)相对旋转次数的总值即总转数(或总小时数)。
轴承疲劳寿命的影响因素非常多,无法全部加以估计,通过标准试验条件也很难消除,造成轴承实际疲劳寿命有很大的离散性。在机械行业中,一般以L10寿命作为衡量标准,它的可靠性是90%,它是一个概率结果,表示该批轴承中有90%在疲劳剥落发生前能达到或超过此转数(或小时数),与具体单个轴承的实际工作寿命不一定完全一致[2]。在ISO推荐标准中,L10的涵义与上述理论基本相同,目前世界各国都遵从上述规定[4]。
随着轴承研究工作不断深入,轴承的重要性能:疲劳寿命及可靠性,已引起各轴承设计、生产单位和用户的广泛关注。但由于疲劳寿命的影响因素太多,加上轴承疲劳寿命理论很零散,仍需完善,进行疲劳寿命的研究、理论开发和优化,是轴承寿命理论发展的大趋势。
3 滚动轴承疲劳寿命理论的发展过程
滚动轴承疲劳寿命理论的发展历程包括了Weibul分布、载荷容量理论、L-P理论、修正理论发展、新寿命理论发展、ISO 281:1990/ Amd.1:2000理论等几个阶段。
3.1 Weibul分布
1939年,weibull提出的认为疲劳裂纹产生于滚动表面下最大剪切应力处,扩展到表面,产生疲劳剥落。weibull给出了生存概率S与表面下最大剪切应力τ、应力循环次数N和受应力体积V的关系[5]:

3.2 载荷容量理论
1947年,Lundberg和Palmgren一起提出了滚动轴承的载荷容量理论(L-P公式)[6]。该理论认为:接触表面下,平行于滚动方向的最大交变剪切应力决定着疲劳裂纹的发生。在考虑到材料冶炼质量对寿命的影响时指出,应力循环次数越多、受力体积越大,则材料的疲劳破坏概率就越大,并提出了统计处理接触疲劳问题的指数方程:

3.3 L-P理论
1901年,R. Stribeck将赫兹弹性接触理论应用到轴承工程学中,首次宣称轴承寿命是由材料疲劳破坏所致,并将寿命与允许载荷相联系,该观点奠定了轴承疲劳失效机理的基础[4]。
传统的滚动轴承寿命理论[4][7][8][9]是指轴承疲劳寿命计算公式的创始人Lundberg和Palmgren,先后于1947年和1952年创立的动态剪切应力轴承寿命学说(简称L-P理论),即轴承或轴承组的基本额定寿命为可靠度90%时的寿命,它以轴承工作表面出现疲劳剥落之前所完成的工作转数,或一定转速下的工作小时数来计算。
L-P理论轴承寿命基本方程是:

式中:C——轴承的额定动载荷;
P——轴承的当量动载荷;
ε——参数(对球轴承ε=3,滚子轴承ε=10/3);
L10——可靠性为 90%的轴承基本额定寿命,106r。
该公式1962年由ISO列为推荐标准ISO/ R281/1—1962,并于1977年修正为正式的国际标准ISO/R281/1—1977[6]。
3.4 滚动轴承修正理论的发展
20世纪60~70年代,轴承生产中已采用组织均匀、非金属夹杂物含量极少的优质钢。通过轴承可靠性统计数据的积累,能将轴承寿命与其破坏概率(以%计算)联系起来,接触—流体动力学润滑理论有了发展,而该理论能够分析评价润滑材料性能对轴承寿命的影响,而且滚动轴承的应用实践也证实,试验所确定的轴承实际寿命与计算寿命出入很大。因此,需要对Lundberg-Palmgren理论进行补充,于是修正的滚动轴承寿命理论引入了三个修正系数[7][8]:a1、a2、a3。

式中: n——所需轴承的可靠度与100%可靠度间的差值;
a1——可靠性系数;
a2——材料系数,包括材料、设计和制造等影响因素;
a3——工作条件系数,包括润滑剂、润滑剂清洁度、逆向温度和装配条件等影响。
为了说明轴承在参考条件下运转与实际环境之间的关系,对传统的寿命理论公式加以扩展,包括润滑、载荷区域及游隙等一些影响轴承性能的环境因素[3]。在轴承选型分析时,需要考虑使用以下系数作为轴承寿命修正系数。

其中,a= a1a2a3
式中:a——轴承寿命修正系数;
a1——可靠性修正系数;
a2——轴承材料修正系数;
a3——环境条件修正系数;
a3=a3ka3la3m
式中:a3k——载荷区修正系数;
a3l——润滑修正系数;
a3m——偏心修正系数。
实践表明,滚动疲劳微裂纹的产生可分为源于表面和次表面两种。由于科学试验技术的发展,Tallian于1996年发表了当代轴承寿命预测模型,该模型考虑了诸多的寿命影响因素,进一部调整充实了L-P寿命理论,这就是通常所说的T理论[4]。
3.5 滚动轴承新寿命理论的发展
1984年Ioannides和Harrix提出:“当轴承受载体材料在承受一个低于疲劳持久极限值的应力载荷时,受载体不会发生疲劳失效的新寿命理论(简称I-H理论)”,对L-P理论进行了修正[4]。
20世纪70年代后期, SKF工程研究中心在轴承疲劳寿命试验中观察到超长寿命现象[8],该中心依据新理论提出了新的修正寿命计算方程:

式中:a23——根据润滑剂粘度系数k=v/v1来查取,见图1;

图1 a23值的确定
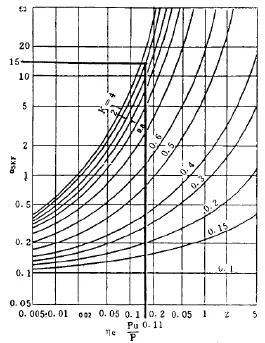
图2 aSKF值的确定
v——轴承实际工作温度下的粘度;
v1——按给定图表查取的润滑油基础粘
度。
在k∈[0,14]时,k越大,a23也越大,相应的轴承寿命越长。当k>4时,a23趋于恒等于k=4时的相应值。
SKF工程研究中心根据轴承载荷低于某一极限将不发生失效的新理论提出了新的寿命计算方程[7] [8] [9]:

aSKF是轴承寿命综合修正系数(又称SKF寿命修正系数)[10][11],该中心公布了SKF样本中各种类型轴承的aSKF取值方法:aSKF由k及ηc•Pu/P查图 2选取。其中,
k——粘度系数,取值方法同上;
ηc——润滑剂污染系数,取值方法见表1;
Pu——轴承疲劳持久极限载荷(N或kN);
P——轴承当量动载荷(N或kN)。
新的寿命理论计算方法引入了疲劳持久极限的概念。通过对表面下应力场充分的试验研究和分析,能对观察到的表面下应力分布及轴承寿命的改善提出合理的解释。

表1 润滑剂污染系数
同时,该模型还考虑以前在滚动轴承疲劳寿命预测中被忽略的许多因素,如表面摩擦及表面局部缺陷(凹坑和表面划伤等)的影响。轴承材料的发展及制造技术的改进,使现代轴承寿命较传统材料及技术制造的轴承寿命有显著提高。目前这一理论仅在SKF内部使用[11]。
3.6 ISO 281:1990/Amd.1:2000理论
IS0281:1990/Amd.1:2000 寿命计算式[5]:

该公式中的修正系数aXYZ考虑到材料、润滑、环境、杂质颗粒、套圈中内应力、安装和轴承载荷等因素对轴承寿命的影响。目前该公式已被我国正式引用并作为我国滚动轴承行业产品寿命的推荐性国家标准GB/T6391-2003。
4 分析与比较
综上所述,滚动轴承的疲劳寿命是轴承的一个非常重要的质量指标,weibull分布和滚动轴承的载荷容量理论只是简单反映出轴承的生存概率即寿命与其影响因素的比例关系,没有公式化,更没有具体量化,影响寿命预估的可靠性。
传统的滚动轴承寿命理论即L-P理论简单地考虑了载荷变化对寿命的影响,没有对轴承的材料、使用的可靠度、润滑、使用时的污染情况等诸多因素进行深入研究和探讨,从工程实践来看,易造成轴承寿命计算与实际不相符,从而影响轴承的有效使用。
滚动轴承修正理论对传统的理论寿命公式加以扩展,除考虑材料、使用的可靠度外,还涵盖了润滑、载荷区域及游隙等一些影响轴承性能的环境因素,每一因素对应一参数,每个参数通过相关的公式或图形就能得到确定,因此,这些因素的考虑和参数的确定,使滚动轴承寿命预估更符合实际,极大改善了轴承的使用性能,从更深层次上影响滚动轴承的设计和制造等领域。修正寿命方程适用于一般工况下的轴承寿命预测。
滚动轴承的新寿命理论将诸多寿命影响因素转化为一个综合修正影响系数aSKF,并且aSKF还考虑以前在滚动轴承疲劳寿命预测中被忽略的许多因素,如表面摩擦及表面局部缺陷(凹坑和表面划伤等)对寿命的影响,这是其优点,但是众多因素只用一个参数反映,难免“心有余而力不足”,并且参数选择过于复杂化,不够直观,造成使用困难。
ISO 281:1990/Amd.1:2000理论中的修正系数aXYZ考虑到材料、润滑、环境、杂质颗粒、套圈中内应力、安装和轴承载荷等因素对轴承寿命的影响,这一系数与新寿命理论的综合修正系数aSKF道理基本一致,亦不够直观,造成使用困难。
因此,滚动轴承修正理论比较贴合实际生产的需要,但是其影响因素过于简单和片面。基于此,作者认为既要考虑到常见、重要因素的影响,又要能较好反映出这些重要因素对寿命是怎样一个影响趋势,他们之间是否能够通过直接的公式或者图形进行具体的量化,保证每个影响因素的针对性,实效性。
5 结束语
结合滚动轴承疲劳寿命概念的介绍,对滚动轴承的疲劳寿命的各个发展阶段进行了详细分析,提出了每个阶段的寿命计算公式,并分析了其应用特点,指出了轴承疲劳寿命的研究方向。藉此,希望对从事轴承设计、制造、研究的同志们以启示。
[1] 杨晓光 译.计算轴承寿命的新方向[J].机械设计(日),39(13).
[2] 王 勇.滚动轴承寿命计算[J]. 研究与设计, 2009, (7): 14-18.
[3]于宏伟.轴承的理论寿命和修正寿命计算方法浅论[J].设计与开发,2009, (3):39-41.
[4] 郭婧.滚动轴承疲劳寿命综述[J].甘肃科技, 2006, (4):133-134.
[5] 李兴林.滚动轴承疲劳寿命试验新进展[J].结构与强度, 488-450.
[6] 李兴林,李俊卿,张仰平等.滚动轴承快速寿命试验现状及发展[J].轴承,2006,(12):44-47.
[7] 杨 洁.新的滚动轴承寿命理论计算方法 [J]. 西部探矿工程, 2004,(11):147-148.
[8] 杨 洁,张晓东.滚动轴承寿命计算方法的分析与应用[J]. 石油机械, 2004(5): 27-29.
[9] 刘耀中.Timken.滚子轴承寿命计算[J].轴承,2004(1):46-48.
[10]〔美〕DANIELR.SNYDER. 轴承寿命的精确计算[J]. MACHINEDESIGN/MARCH.1992:12.
[11] SKF.General Catalogue.4000E [M].1989.
(编辑:王立新)
Research and analysis of dvelopment of life calculation method for rolling bearing
Zhu Liangliang1, Lin Sumin1, Ji Xiaomin2
( 1. Yangling Vocational and Technical College, Xianyang 712100, China; 2. Xi′an University of Science and Technology, Xi′an 710054, China)
This paper introduces the concept of rolling bearing fatigue life, and the development course of rolling bearing fatigue life in detail, analyzes the characteristics of the theoretical calculation of different periods of life for your reference.
rolling bearing; fatigue life; shear stress; fatigue spalling
TH133.33
A
1672-4852(2014)03-0003-04
2014-03-22.
朱亮亮(1982-),男,讲师,硕士.

