基于多模型融合的木材表面缺陷图像快速识别1)
李 佳 王阿川 马欣然
(东北林业大学,哈尔滨,150040)
责任编辑:张 玉。
木材缺陷检测是木材加工工业中必不可少的一步,准确快速的识别出木材缺陷的轮廓,对提高木材的利用率、木制品质量和企业的经济效益具有重大的意义。对实现木材缺陷的自动检测系统而言,木材缺陷图像的识别是问题研究的重点。现有的检测方法有多种,包括:人工检测、X射线检测、计算机视觉检测、红外线检测、机械应力检测等[1];对木材缺陷图像进行分割、分析,国内外学者大多采用阈值法[2]、一阶统计特征法[3]、二阶统计特征法[4]以及Gabor变换法[5]等。但是,由于木材缺陷种类繁多,缺陷的形态、颜色、大小等各有差异,以及自然生长的原木所形成的纹理等因素给缺陷识别过程带来了诸多困难,致使目前的检测方法以及硬件设备均存在着各种局限性[6]。目前,识别单一种类、单个数量缺陷的算法较多,对复杂背景的多缺陷识别效果并不是很好。
基于PDE(Partial Differential Equation)的图像处理方法,近年来受到了研究人员的关注,比较有代表性的是Chan等[7]提出的水平集图像分割方法。但是,经典C-V(Chan and Vese/Active Contours Without Edges)模型,需要定期重新初始化水平集函数,并且演化速度明显依赖于演化曲线的初始位置,抗噪能力差,对目标灰度不均匀及背景复杂的图像处理效果不好[8]。GAC(Geodesic/Geometric Active Contour)模型,是由Caselles等[9]、Kichenassamy等[10]提出的一个新的扩展版本的snake模型。然而,GAC模型对初始条件非常敏感,选择的初始轮廓线离目标越近,识别出来的效果越好;但是,现实情况下,很难保证每次选择的初始轮廓都是一次很好的选择,往往在多次试验后还是得不到好的识别结果。GAC模型只能识别闭合及凸型的缺陷轮廓,对轮廓线较模糊、有断点或者轮廓某些位置有凹陷的情况,识别结果轮廓线不能收敛到目标的真实轮廓边缘,这是因为在轮廓的演化过程中很可能就停留在局部极小值处[11]。
本文将C-V、GAC二个模型融合起来,提出一种基于全局最小化活动轮阔快速识别模型。C-V模型和GAC模型的结合,实现了二者性能的互补。经过实验证明,不管图像是否具有复杂背景,还是具有多个目标缺陷,本文改进过的新模型算法不受缺陷类型、大小、数目和形状的限制,能够做到准确、快速识别木材表面的节子、孔洞、腐朽、空心以及复杂纹理背景的多目标缺陷,具有对各类木材表面缺陷图像进行识别的普遍适用性。
1 模型的改进及算法实现
1.1 GAC模型
GAC模型的能量形式为:

式中:d s为长度的欧氏元素;LC是闭合演化曲线C的长度;▽I表示图像I的梯度;LRC是加权弧长;g(︱▽I︱)为边缘停止函数,作用是使C向着图像中目标的边缘靠近,并稳定在边缘上,然而,当图像中目标边缘有较深的凹陷时,GAC模型可能停止在某局部极小值状态,不能完整分割。
1.2 ROF模型
Rudin-Osher-Fatemi提出的总变分模型,能量形式为[13]:

1.3 C-V模型
C-V变分模型:

式中:f(x,y)是给定的原始图像;ΩC是图像域Ω的一个闭子集;PΩC是集合ΩC的周长;μ≥0、λ1>0、λ2>0为调节系数;标量c1表示区域ΩC内的平均灰度;c2表示区域ΩΩC内的平均灰度。第二项(x,y)-c1)2d x d y和第三项分别是内部区域和外部区域的灰度值与标量c1和c2的平方误差,是实际图像与假定的“分片常数”图像之间的偏离。由于此模型综合利用了图像的全局信息,因此,通过最优化能量泛函得到的是全局最优图像分割结果。
1.4 模型改进和求解
1.4.1 模型的改进
由于侧地线/活动轮廓GAC模型,是通过图像的梯度识别目标边界,因此,该模型可以识别木材表面缺陷轮廓比较清晰且封闭的凸型区域,但其识别效果依赖于初始轮廓的选择。而基于C-V的无边缘活动轮廓(ACWE)模型,是利用同质区域信息对目标边界进行检测,利用该模型可以识别木材表面缺陷轮廓不是太清晰(尤其是背景比较复杂的缺陷),仅适合于分段光滑区域。因此,结合每个模型各自的特征,本文提出,将经典GAC模型与C-V模型结合在一起,从而使图像识别独立于初始轮廓的选择,同时对目标轮廓模糊、背景复杂的图像也能更好的识别。
本文通过将经典GAC模型和基于C-V的ACWE模型,统一于一个全局最小化框架中,采用基于图像的梯度及同质区域的边缘检测,实现同时对木材表面缺陷目标边缘检测。因此,文中结合GAC模型与ACWE模型互补方法,创造一个改进的木材表面缺陷分割模型。ACWE变分模型如下:
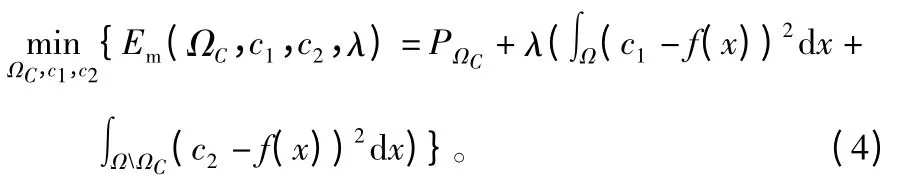
式中:f(x)是所给木材表面图像;ΩC是图像区域Ω的一个闭子集;PΩC是集合ΩC的周长;λ是一个任意正参数,其控制正则化过程和解的忠诚项之间的平衡;c1、c2∈R;若ΩC是固定的,最小化能量泛函(Em)的值c1、c2,是ΩC内部与外部区域的均值。最后,PΩC项用于在集合ΩC上施加光滑约束,从而可以分离ΩC的分段常数区域。
最小化问题(4)是非凸性的,两步算法是一个自然的方法确定一个解(ΩC,c1,c2)。其中:c1、c2是最先计算的,然后不断更新区域ΩC,以最小化(4)式的能量泛函(Em)。Chan等提出,用水平集函数的Heaviside函数,描述区域ΩC和Ω/ΩC。因此,能量泛函(Em),可根据水平集函数∅写成:
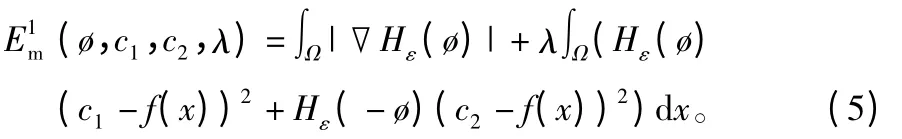
式中:Ω是图像区域,Hε是正则化Heaviside函数。
对于能量方程(5),本文提出(非严格)凸能量泛函对其进行改进并求解,引入加权TV范数,对任意给出的木材表面图像f∈L1(Ω)以及任意正常数λ有:


由此,实现了标准活动轮廓模型与ACWE模型之间的融合。λ是一个任意正参数,其控制正则化过程和解的忠诚项之间的平衡,对木材表面缺陷轮廓不太清晰、背景比较复杂时,主要靠同质区域方法识别木材缺陷,即主要靠第二项识别,这时λ的取值比较大;而当木材表面图像,缺陷轮廓比较清晰时,主要靠第一项识别,第二项贡献小一些,这时λ的取值比较小。而且,能量E2提供了活动轮廓模型的全局最小值。其中C是集合ΩC的边界,是E2(…,c1,c2,λ)的一个全局最小值。
对于ACWE模型,u是能量泛函E2中测度为1的同质区域,意味着当u的最小化不是受限的(如0≤u(x)≤1),此演化方程没有稳定的解。因此,该受限最小化问题开展分割任务,实际上是如下最小化问题:

根据凸分析理论可知,式(9)的凸约束最小化问题与(10)的凸性非约束的最小化问题,有同样的最小化集合。从而得到改进的木材表面缺陷图像检测模型:
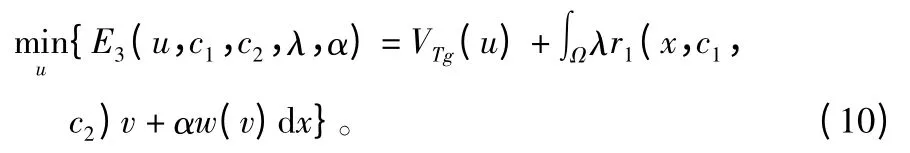
式中:v(ξ):=max{0,2∣ξ-0.5∣-1}是一个惩罚函数提供比λ足够大的常数α,如α>(λ/2)‖r1(x)‖L∞(Ω)。
能量(10)是凸性但是不严格凸,意味着E3不拥有不是全局最小值的局部极小值。因此,任意能量E3的极小值都是全局极小值。
1.4.2 模型求解及模型的数值化算法
可以用标准Euler-lagrange方程技术和基于算法的梯度下降流,计算E3的一个全局极小值。然而,此数值最小化方法是非常慢的。因此,为了提高识别速度,采用基于TV范数对偶化的方法[15]求解此模型。对式(10)进行变分模型的凸正则化得式(11):
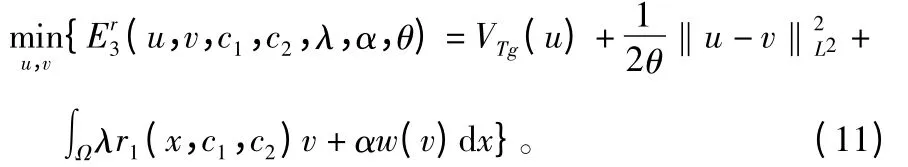
式中:参数θ>0是较小的数,几乎有f=u+v;函数u表示图像的几何结构信息,即分段光滑区域,表示木材缺陷图像的结构部分;函数v表示存储于给定木材缺陷图像中的纹理及噪声部分。
因为能量泛函E'3是凸性的,因此其最小值可以通过关于u和v交替最小化计算得到;并不断迭代,直到收敛得到。因此,下面的最小化问题是合理的:
(1)v固定,求解(12),可求得u。

(2)u确定,求解(13),可求得v。
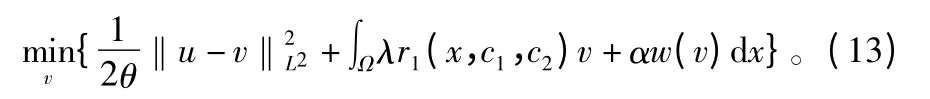
(12)的解由u=v-θdiv p给出。式中:p=(p1,p2)由g(x)▽(θdiv p-v)-∣▽(θdiv p-v)∣p=0给出。则之前的方程可以通过固定点的方法求解。P0=0,并且

(13)的解由(15)给出。

迭代方案(14)直接进行;方程(14)和(15)不断迭代,最小化能量(11)。当然,常数c1、c2每迭代一定次数后定期更新。
本文的分割模型,在目标与背景之间的对比度很低的情况下,不仅改进了GAC模型,而且改进了ACWE模型,使二者互补,从而独立于初始轮廓位置。改进的模型,使用加权VT范数对偶化的方法提高了识别的速度。
本文提出的分割模型框架,统一了图像分割(snake模型)、ACWE图像分割模型。事实上,最小化问题中,函数v的引入很自然的捕捉到了图像的纹理部分。图像分解,包括将一个图像分离成它的几何/分段平滑区域表示的结构部分和纹理部分(包括纹理和噪声)。因此,能量泛函(10)的最小化,导出了分割模型的全局最小值;同时,演示了图像的分解,其改进了分割任务。
1.4.3 模型求解的算法实现
首先,选择时间步长0<t≤1/8,以及初始值β、θ、λ,设I为输入的木材表面缺陷图像。
(1)计算边缘检测函数,对图像进行平滑处理。对输入图像I,进行方差为σ的高斯滤波变换,计算边缘检测函数:G(I)=1/(1+β∣▽(I*Gσ)∣2),β是一个任意的正常数。
(2)初始化图像参数。选择初值u0=G(I)、v0=u0、p0=(p1,p2)=0。
(3)进行迭代分割处理。根据式(14)、式(15),不断迭代更新u、v,从而最小化能量泛函(11)。每次迭代n次后,依据区域灰度均值重新划分区域;不断迭代,直到收敛分割出所有缺陷为止;则得图像的结构部分u和纹理部分v。
2 结果与分析
参数θ表示本模型求解时迭代求解的步长,一般若要识别的木材缺陷比较小时,则θ取值比较小,但求解速度要慢些;若待识别木材缺陷比较大,θ取值较大时,求解速度要快些。函数v表示木材缺陷图像的纹理及噪声部分。
实验在Pentium 2.93微机上用Matlab7.0实现。为了使边缘监测函数G(I)能更快收敛到木材表面缺陷目标,经过多次试验,本次试验模型参量β=0.000 768 9;根据模型(10)中λ参数的作用,经试验,一般对木材非纹理图像λ=0.000 035,即主要靠模型(10)的第一项求解;对木材纹理图像λ=400 000 0,即主要靠模型(10)的第二项求解;θ取值见表1。

表1 木材表面缺陷图像识别参数
利用本文算法,分别选取256×256的带纹理和不带纹理的木材、单板表面缺陷灰度图像,用Matlab7.0进行实验(见图1~图7)。图1~图4,为不带纹理的木材及单板表面缺陷图像;图5~图7,为带纹理的木材及单板表面缺陷图像。图1~图7中的a图,均为木材、单板缺陷原图像;b图,为使用本文方法在Matlab下进行识别后得到的实验结果图;c图,为使用基于改进C-V模型方法[14]在Matlab下识别的结果图;d图,为使用GAC模型在Matlab下进行识别的结果图。本文算法各个实验图像的参数值见表1,本文算法与C-V模型及GAC模型的运行时间对比见表2;本文算法、C-V模型、GAC模型的空间复杂度,分别为Ω(n)、Ω(n3)、Ω(n)。

图1 木材孔洞缺陷图像识别
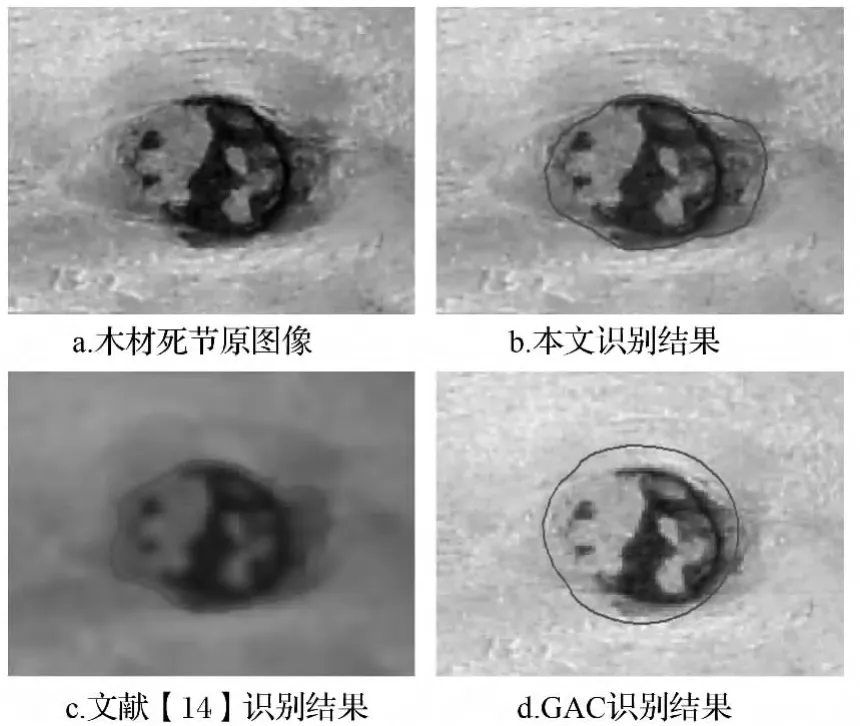
图2 木材死节缺陷图像识别
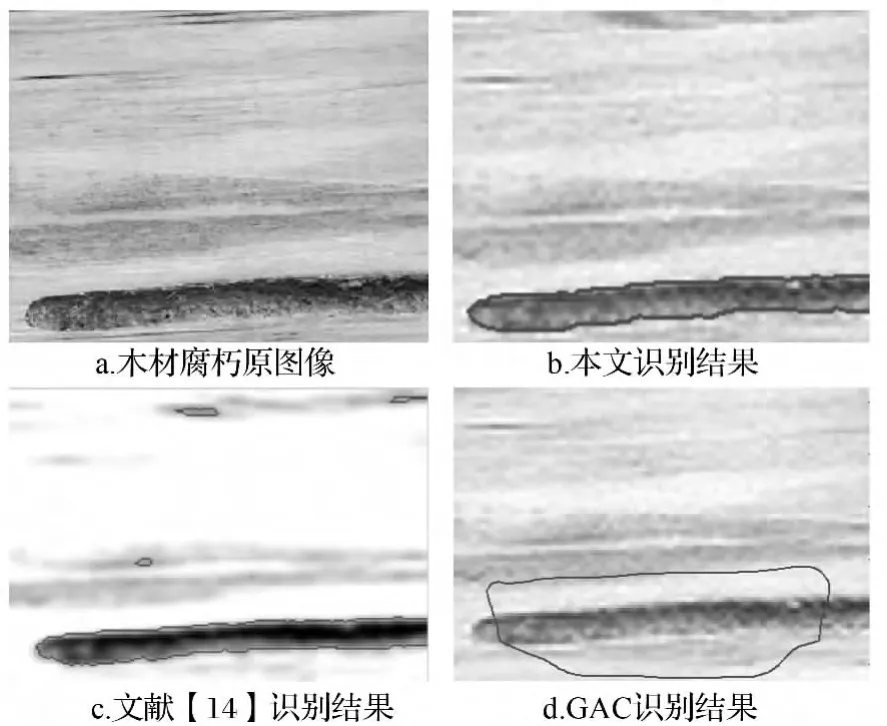
图3 木材腐朽缺陷图像识别
从表1、表2可看出,θ和n的取值影响着实验效果,N的取值影响识别速度。当目标与背景颜色相近(图3),或者复杂背景对目标识别有影响(图5、图6),或者缺陷目标较小(图4、图7)的时候,θ取值较小;因为在这些情况下,θ增大时会导致分割轮廓线不能够准确的停留在缺陷与背景的边界处,实验结果会出现边缘泄露。当缺陷图像中有较小的缺陷目标时(图4、图6、图7),迭代步长n的取值较小;因为,若迭代步长变大,当被识别目标小于迭代步长时,会导致较小的缺陷目标被忽略。因此,在使用本文方法时,根据被识别对象情况,通过实验确定θ、n的大小,可得到很好的识别效果。其次,缺陷目标与背景间的颜色,差距越小识别越困难(图2、图3、图5);相应的要增加总的迭代次数N,较多次的重新划分区域进行迭代运算,才能使轮廓线更准确地停留在缺陷目标边缘,但是,这也会增加识别时间。

图4 单板多节子缺陷图像识别
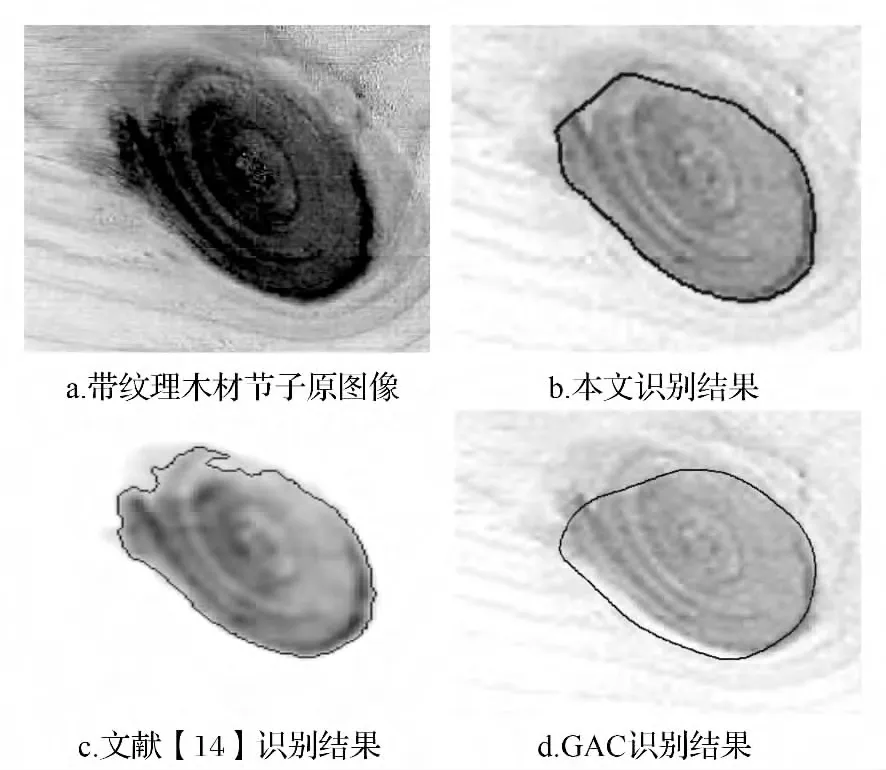
图5 带纹理木材活节缺陷图像识别

表2 3种算法的运行时间 s
根据上述实验结果可发现,C-V模型对于单缺陷目标图像的识别,其识别结果还是不错的;但是,对于具有复杂背景和多目标缺陷的图像而言,识别结果就出现了边界泄露的情况,并且在无缺陷目标的位置呈现出了多余的轮廓线。GAC模型只能识别具有单个缺陷的图像,而且轮廓线明显不能准确的停留在目标的真实边缘处。当图像中有多个待识别目标时,GAC模型不能一次性准确的分割出各个缺陷目标的轮廓和位置,而结果到底是分割出哪一个目标轮廓,在很大程度上取决于初始轮廓线位置的选择。本文的模型算法,则不受木材表面缺陷的类型、大小、形状、数量和纹理的影响,对于节子、孔洞、空心、腐朽以及多缺陷目标等各类木材及单板表面缺陷图像,都能够准确的识别出木材缺陷的轮廓。其次,从表2和3种算法空间复杂度的对比数据看,本文算法平均在1 s左右就能够得到令人满意的实验结果,C-V模型算法平均需要3s左右的时间,GAC模型算法平均需要几十秒。本文提出的算法,在不增加空间复杂度的情况下,提高了速度,实现了快速识别的目的。
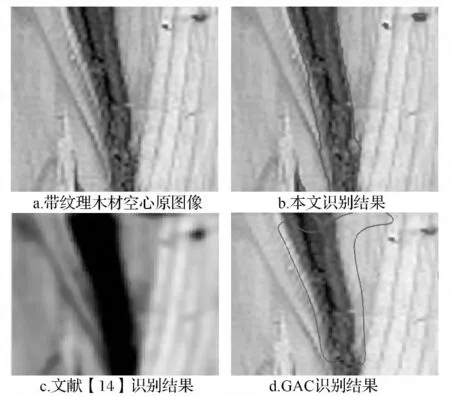
图6 带纹理木材空心缺陷图像识别

图7 带纹理的单板多节子缺陷图像识别
3 结论
本文结合C-V模型、GAC模型、ROF模型和TV范数对偶化的方法,快速准确的实现了对木材节子、孔洞、腐朽、空心等缺陷图像和单板多节子缺陷图像的识别。实验结果表明:本文提出的多模型融合的算法,对各种木材表面缺陷图像的识别具有很好的效果,基本上没有轮廓泄露,也没出现丢掉部分目标的情况。基于TV能量对偶化的算法,引入了边缘检测函数g,因此,尽管图像中存在目标与背景对比度变化较低的地方或者是复杂背景有纹理的状况,此算法还是可以成功的捕捉到目标对象,并识别出目标对象的轮廓边缘。而且,本文算法,避免了水平集方法的一贯缺点,不依赖于初始轮廓线的选择,并提高了识别速度。该算法,可应用于对各种木材表面缺陷的识别,具有一定的通用性。
[1]尹建新,计时鸣.基于计算机视觉的木材表面缺陷检测方法研究[D].杭州:浙江工业大学机械电子工程系,2007.
[2]邹丽晖,白雪冰.图像分割技术在木材表面缺陷识别中的应用[J].森林工程,2007,23(1):27-29.
[3]Packianather M S,Drake P R.Neural networks for classifying images of wood venner(Part 2)[J].The International Journal of Advanced Manufacturing Technology,2000,16(6):424-433.
[4]Conners R W,Mcmillin CW,Lin K,et al.Identifying an locat-ing surface defects in wood:Part of an automated lumber pro-cessing system[J].IEEE Trans on PAMI,1983,5(6):573-583.
[5]Lampinen J,Smolander S.Self-organizing feature extraction in recognition of wood surface defects and color images[J].International Journal of Pattern Recognition and Artificial Intelligence,1996,10(2):97-113.
[6]王克奇,白雪冰.木材表面缺陷的模式识别方法[M].北京:科学出版社,2011.
[7]Chan T F,Vese L A.Active contours without Edges[J].IEEE Trans Image Processing,2001,10(2):266-277.
[8]何瑞英.C-V活动轮廓模型的研究[D].重庆:重庆大学,2009.
[9]Caselles V,Kimmel R,Sapiro G.Geodesic active contours[J].International Journal of Computer Vision,1997,22(1):61-79.
[10]Kichenassamy S,Kumar A,Olver P,et al.Conformal curvature flows:from phase transitions to active vision[J].Archive for Rational Mechanics and Analysis,1996,13(4):275-301.
[11]Xavier Bresson,Selim Esedoglu,Pierre Vandergheynst,et al.Fast global minimization of the active contour/snake model[J].Journal of Mathematical Imaging and Vision,2007,28(2):151-167.
[12]Rudin L I,Osher S,Fatemi E.Nonlinear total variation based noise removal algorithms[J].Physica D,1992,60(1/4):259-268.
[13]陈利霞,冯象初,王卫卫,等.加权变分的图像去噪算法[J].系统工程与电子技术,2010,32(2):392-395.
[14]王阿川,于琳瑛,曹军.基于AOS的扩展C-V模型及背景填充耦合的单板节子缺陷识别[J].林业科学,2011,47(5):106-111.
[15]Chambolle A.An algorithm for total variation minimization and applications[J].Journal of Mathematical Imaging and Vision,2004,20(1/2):89-97.

