Estimating water storage changes and sink terms in Volta Basin from satellite missions

Vagner G. FERREIRA*, Samuel Ato ANDAM-AKORFUL, Xiu-feng HE, Ru-ya XIAO

1. School of Earth Sciences and Engineering, Hohai University, Nanjing 210098, P. R. China

2. Department of Geomatic Engineering, Kwame Nkrumah University of Science and Technology, Kumasi, Ghana

3. Institute of Satellite Navigation and Spatial Information Systems, Hohai University, Nanjing 210098, P. R. China

Estimating water storage changes and sink terms in Volta Basin from satellite missions

Vagner G. FERREIRA*1, Samuel Ato ANDAM-AKORFUL2,3, Xiu-feng HE3, Ru-ya XIAO3

1. School of Earth Sciences and Engineering, Hohai University, Nanjing 210098, P. R. China

2. Department of Geomatic Engineering, Kwame Nkrumah University of Science and Technology, Kumasi, Ghana

3. Institute of Satellite Navigation and Spatial Information Systems, Hohai University, Nanjing 210098, P. R. China

The insufficiency of distributed in situ hydrological measurements is a major challenge for hydrological studies in many regions of the world. Satellite missions such as the Gravity Recovery and Climate Experiment (GRACE) and the Tropical Rainfall Measurement Mission (TRMM) can be used to improve our understanding of water resources beyond surface water in poorly gauged basins. In this study we combined GRACE and TRMM to investigate monthly estimates of evaporation plus runoff (sink terms) using the water balance equation for the period from January 2005 to December 2010 within the Volta Basin. These estimates have been validated by comparison with time series of sink terms (evaporation plus surface and subsurface runoff) from the Global Land Data Assimilation System (GLDAS). The results, for the period under consideration, show strong agreement between both time series, with a root mean square error (RMSE) of 20.2 mm/month (0.67 mm/d) and a correlation coefficient of 0.85. This illustrates the ability of GRACE to predict hydrological quantities, e.g. evaporation, in the Volta Basin. The water storage change data from GRACE and precipitation data from TRMM all show qualitative agreement, with evidence of basin saturation at approximately 73 mm in the equivalent water column at the annual and semi-annual time scales.

equivalent water column; evaporation; GLDAS; GRACE; hydro-geodesy; TRMM

1 Introduction

About 20 million people in the countries of Ghana, Burkina Faso, Mali, Benin, Togo, and Ivory Coast make their homes within the Volta Basin. According to Kasei et al. (2010), the population growth rate in the region is almost 3% per year, much higher than the global average of 1.1%, placing increased pressure on land and water resources. The total surface area of the Volta Basin is 407 093 km2, and, for that reason, the climate, soils, and vegetation are largely variable in different regions. Most streams within the basin are ephemeral; it is thus extremely difficult to find potable water in most parts of the basin during the dry season.Therefore, water storage changes are of particular importance in areas with arid or semi-arid climates within the Volta Basin. Traditionally, large amounts of in situ data from different measuring points are required to monitor water storage changes. However, as noted by Xie et al. (2012), river systems in Sub-Saharan Africa are poorly monitored and many basins are ungauged. Milzow et al. (2011) studied the capability of remote sensing observations in conjunction with satellite gravimetry in hydrological model calibration over a poorly gauged catchment. Deus et al. (2011) quantified water balance modeling in a semi-arid environment with limited in situ data using remote sensing coupled with satellite gravimetry.

With more than 10 years in orbit, the twin satellites of the Gravity Recovery and Climate Experiment (GRACE) have been monitoring the earth’s gravity field in the spatial and temporal domains. According to Wahr et al. (1998), the largest-amplitude and most varied time-dependent signals are related to water storage variability on land. The GRACE satellite mission’s sensitivity to various water mass variations has been clearly demonstrated over recent years (Vey et al. 2012, and references therein). It should be noted that GRACE measures vertically integrated water storage anomalies and cannot separate contributions from individual stores (i.e., surface stores, soil layers, ice including snow, groundwater reservoirs, and biomass) without other independent data (Cazenave and Chen 2010). There have been a variety of efforts to combine GRACE-derived water storage changes with other data sets to constrain source (precipitation) and sink (evaporation and runoff) terms in the water balance (Crowley et al. 2007). Across West Africa, only a few GRACE applications have been carried out, with emphasis on the Niger Basin and the Sahel region (Grippa et al. 2011; Hinderer et al. 2011) and on basins in Sub-Saharan Africa (Xie et al. 2012). Grippa et al. (2011) showed that GRACE data can reproduce water storage inter-annual variability over the Sahel region. Xie et al. (2012) have used seven years of GRACE data to calibrate a semi-distributed regional scale hydrological model, the soil and water assessment tool (SWAT).

There are no results in the literature regarding to the relation between source and sink terms in the terrestrial hydrological water balance in the Volta Basin when using GRACE-derived water storage change and precipitation data from the Tropical Rainfall Measurement Mission (TRMM), as proposed by Crowley et al. (2007). Hence, the aim of this study is to characterize the water storage variations in the Volta Basin, and to quantify the extent to which precipitation dominates the seasonal water storage variations. In addition, we examined the temporal variations of the difference between precipitation data (source term) from TRMM and GRACE-derived water storage changes within the Volta Basin to access evaporation plus runoff (sink terms).

2 Materials and methods

2.1 Water storage anomalies from GRACE

The earth’s global gravity field is commonly described in terms of the shape of the geoid:the equipotential surface that optimally fits (in the least squares sense) the mean sea level over the oceans (Wahr et al. 1998). Changes of mass distribution in the earth system due to variations in continental water storage cause spatiotemporal changes of the geoid (Ramillien et al. 2008). To convert variations of the geoid into the equivalent water column (h), a method proposed by Wahr et al. (1998) can be applied, where the water storage anomalies expressed in terms of the equivalent water column are

for a given month t, where θ is the colatitude, λ is the longitude, R is the mean radius of the earth (6 371 km),is the normalized associated Legendre functions of degree n and order m, andandare the residual surface density coefficients obtained from the following relations (Wahr et al. 1998):

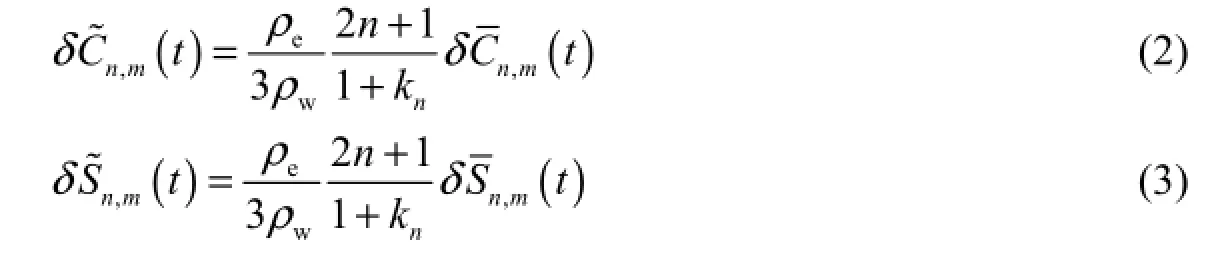
where ρeis the average density of the earth, ρwis the density of water, and knis the load Love number for degree n. Note that Eqs. (2) and (3) define a simple filter that allows conversion of the variations of the geoid into the equivalent water column (usually expressed in mm).

The residual Stokes’s coefficientsin Eqs. (2) and (3) are defined as follows:

where N is the total number of monthly (ith) solutions, and the long-term mean of Stokes’s coefficientsandis removed. The reason for removing the mean field is that it is dominated by the static density distribution inside the solid earth. Removing the static field means that all contributions from the mean stored water are also removed. Thus, only the time-variable component of the water storage can be recovered, i.e., water storage anomalies.

The maps of water storage anomalies, expressed in the equivalent water column calculated with Eq. (1), describe present linear features in the north-south direction called stripes (Ramillien et al. 2005). The presence of these stripes indicates a high degree of spatial correlation in the GRACE errors in short-wavelength components (high frequencies). To obtain coherent results it is necessary to remove stripes using a post-processing method to reduce correlated error with a minimal impact on the real signal (Swenson and Wahr 2006). There exist several methods to compensate for this (Werth et al. 2009). One is to use anempirical method based on polynomial fitting (Swenson and Wahr 2006). Another approach is to use an a priori synthetic model of the observation geometry (Kusche 2007). In this study the polynomial filtering scheme suggested by Chen et al. (2007) was applied to the residual Stokes’s coefficients in Eqs. (4) and (5). For residual Stokes’s coefficients with orders 6 and above, a least square fit degree 4 polynomial was removed from even and odd degree coefficient pairs (Chen et al. 2010). For example, for Stokes’s coefficients of order 6, we fitted a degree 4 polynomial to the even-degree pair (e.g.,and removed the polynomial fit from the coefficients. The same process was applied to the odd-degree pair (e.g.,Chen et al. (2010) call this procedure the de-correlation filter, hereafter abbreviated as P4M6.

After P4M6 filtering, a Gaussian low-pass filter was used to further suppress the remaining short-wavelength errors (Swenson and Wahr 2006). Given the averaging or smoothing radius r, the Gaussian smoothing operator W for a degree n ( 1n≥ ) is defined by a recursive relation (Wahr et al. 1998):

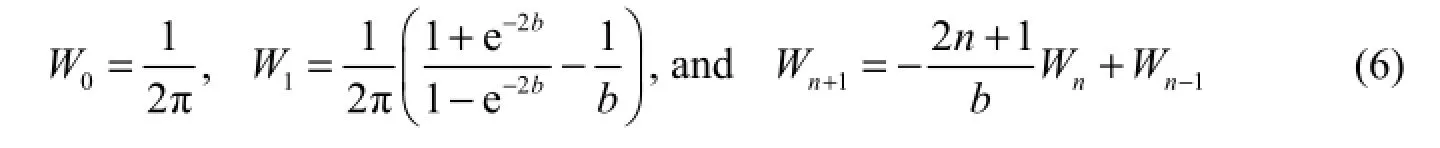
where the parameter b, given the half-height length, is

Following Ramillien et al. (2005), the choice of the r value is a good compromise between spatial resolution and the effect of noise. A 300-km averaging radius was considered because it removes the striping effects, but still allows for study of sub-basin changes.

2.2 Terrestrial water balance

It is well known that water budget methods are based on the principle of conservation of mass applied to some part of the hydrological cycle. Over a land surface of area Ω the mean evaporation rate, E, can be expressed in terms of the water balance equation, as follows (Ramillien et al. 2005):

where P is the areal mean rate of precipitation, Q is the mean net surface runoff rate per unit area from the basin (assumed to include both the surface and groundwater runoff of the area), and S is the water volume stored per unit area. If Eq. (8) is integrated over a sufficiently long period, i.e., decades, the water balance equation becomes a system in a steady state. This implies that for any property S of the system, the partial derivative with respect to t is zero. Integrating and rearranging the terms in Eq. (8) yields

where ΔS is the terrestrial water storage variation in a month, which can be compared with the GRACE data, and t0and t1are the first and last days of the month, respectively. The terrestrial water storage variations ΔS inside the drainage basin are directly computed as the difference between two monthly solutions as (Ramillien et al. 2006)

As runoff and, in particular, evaporation are difficult to measure accurately, an estimate of their combined contributions to the terrestrial hydrological cycle within a specific watershed can be made by combining GRACE data with precipitation data (Crowley et al. 2007).

2.3 Data sets

2.3.1 GRACE data

The data for this study included 74 GRACE monthly solutions, determined by the German Research Centre for Geosciences (GFZ) release 05 (RL05) (see Dahle et al. (2012) for details), covering the time period from December 2004 to February 2011 (January 2011 is missing). These sets of coefficients are complete up to a degree and order of 90. However, the coefficients were truncated at a degree and order of 60. This limit fixes the spatial resolution ρ at approximately 333 km (ρ = πRn ) at the surface of the earth. GRACE does not provide changes of degree 1 coefficients, i.e., C1,0, C1,1, and S1,1, which represent the variation of the earth’s center of mass relative to the fixed terrestrial reference frame (Chen et al. 2005). As the geoid solutions are provided in a terrestrial reference frame, the degree 1 coefficients were set to zero. Because GRACE-derived C2,0is affected by large tide-like aliases, it is necessary to replace C2,0with an independent estimate from satellite laser ranging (SLR). However, GFZ’s approach is to constrain C2,0to an a priori model during the gravity field solution process. This approach achieves the same goal, which is to avoid the errors in C2,0. This means that, when using the GFZ RL05’s solution, it is not necessary to replace the C2,0values, but they can be used directly as given. For additional information we recommend Cheng and Tapley (2004).

2.3.2 Precipitation

The global monthly accumulated precipitation dataset supplied by the TRMM as Level-3 V7 products, more specifically the TRMM 3B43, was used. Owing to the availability of the GRACE products at the time of the study, the time period was limited to January 2005 to December 2010 (a total of 72 data points) with a 0.25° × 0.25° spatial resolution. The precipitation data were also filtered, as water storage anomalies derived from GRACE, by applying a Gaussian filter (smoothing at 300 km). This was necessary for a direct comparison with the GRACE water storage changes. As in Wahr et al. (1998), in spatial representation the Gaussian smoothing operator is defined as

where ψ is the spherical distance between the points (the center of the study area and each grid point).

2.3.3 GLDAS data

Because of a lack of in situ data, a validation of the GRACE-TRMM-derived sink terms, evaporation and runoff, proposed in Eq. (9), using measured data is not possible. However, to analyze the performance of the results, the GLDAS data of evaporation, surface runoff, and subsurface runoff were considered. In this particular simulation, GLDAS drove the Noah land surface model (Rodell et al. 2004a), with observed precipitation and solar radiation included as inputs. A fair comparison with GRACE observations requires that GLDAS fields be spatially filtered in a consistent way. To accomplish this, GLDAS data were filtered as the TRMM data described in section 2.3.2, i.e., a 300-km Gaussian smoothing filter was applied.

3 Results and discussion

As shown by the residual surface density coefficient time series in Eqs. (2) and (3), the water storage anomalies were computed applying Eq. (1), expressed in equivalent water column (h) for the period from December 2004 to February 2011. The missing monthly land water solution data for January 2011 was interpolated from the previous and the next months, i.e., December 2010 and February 2011. To quantify the water storage variations (ΔS) in the Volta Basin for the period from January 2005 to December 2010, the procedure described in Eq. (10) was applied, using water storage anomalies for the period from December 2004 to January 2011. For numerical computations, the water catchment area (Ω) was subdivided into 0.5° × 0.5° grid cells. In this case, 140 grid cells were defined (Fig. 1). For each grid cell, there was an individual water storage ΔS at each epoch t. The variations of the spatially averaged water storageover the specified area using the weighted mean formula were computed as follows:

where ΔΩiis the area of the ith grid cell within the study area ( ΔΩ = (s inθ) Δθ Δλ ). To be consistent with the GRACE data analysis, spatial averages of the precipitation values from TRMM as well as evaporation and runoff (surface and subsurface) from GLDAS, were computed using Eq. (12).

There are variations due to the seasonal effects in the areal averagedand the areal averaged precipitation within the Volta Basin from January 2005 to December 2010 (Fig. 2). The precipitation records show that the high water season occurs normally in July, with the low water season occurring in February. In the case of water storage variations, monthly values generally range from –70 to 70 mm. As expected, the recharge of the water storageis mainly observed between April and September, when the precipitation is generally at its maximum. The largest water storage variation for a single month occurred in July 2008and the minimum in December 2005 (Δ S =− 76 mm).

Fig. 1 Map of Volta Basin and grid cells

Fig. 2 Comparison between monthly precipitation and GRACE-derived water storage changes

The monthly average variation ofand precipitation were estimated for the period from January 2005 to December 2010 (Fig. 3), after the long-term trend was removed from each in order to emphasize short-term changes. The range between the negative and positive extremes ofis 106 mm, indicating that the seasonal hydrologic fluxes in the Volta Basin are high. Wahr et al. (2006) have shown the total error in a single monthly solution to be 15 to 20 mm for an averaging radius of 400 km for the GRACE-derived water storage anomaly. This indicates that GRACE-derived water storage anomalies (as well as the water storage changes) can be applied in the Volta Basin, and consequently will make it a useful tool for investigating shorter-period variations in the area. It appears that there is a phase difference between water storage variations and precipitation of one month in the wet season (Fig. 3).The phase shift indicates that the water storage changes generally precede precipitation. A possible explanation for this phase shift is the evidence of the basin saturation at 58 mm of the equivalent water column.

Fig. 3 Seasonal cycle of water storage changes and precipitation based on data from 2005 to 2010 after removal of linear trend (Error bars represent standard deviation for monthly mean values)

To investigate this supposition, the GRACE and TRMM time series were modeled, taking into account constant, linear, annual, and semi-annual amplitudes as follows:

where τ is a given time point expressed in years; y(τ) is the original input series; the coefficient a1represents an instantaneous trend for the epoch τ0, and τ0is the midpoint of the time span, i.e., 2008; ω= 2πT , where T = 1 year in this study; and k represents the rank of the harmonics (k = 1 and k = 2 correspond to the annual and semi-annual components, respectively). The parameters a1, Ak(the amplitude), and φk(the phase) were estimated through a least squares fitting procedure with their corresponding accuracies, as well as the correlation coefficient (Table 1). Both of these time series are also shown in Fig. 4 with the constant (a0) and linear (a1) terms removed.

Table 1 Estimated trend at epoch 2008, amplitudes, and phases of annual and semi-annual variations of GRACE and TRMM time series, and correlation coefficient

A trend of 1.83 ± 1.10 mm/year that suggests an increase in precipitation over the basin during the period under consideration was seen (Table 1). The Volta Basin shows an increase inof 0.84 ± 0.96 mm per year, which is equivalent to 0.34 ± 0.39 km3per year. It is characterized by wide variability between dry and wet seasons and also from year to year. The signal-to-noise ratio (SNR) of inter-annual trends for the precipitation and water storage changes are 1.7 and 0.9, respectively, indicating that the positive trend in water storage changes is insignificant. At the seasonal time scale, a significant positive correlation (0.91)between the water storage changes and precipitation was found, indicating a high level of agreement between areal averaged water storage changes and precipitation.

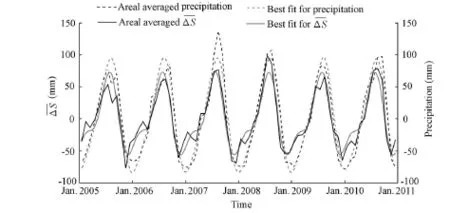
Fig. 4 De-trended areal averaged precipitation andas well as best fit for both time-series

When comparing the phases of the GRACE-derivedand the TRMM precipitation at the annual amplitude (Table 1), a phase lag of −0.42 ± 0.10 months was found. Moreover, we found that the amplitudes are not in close accord, indicating that the annual variation of the water storage within the Volta Basin is dominated by precipitation; as expected, the precipitation tends to bound the water storage changes. This means that the annual signal from the sink terms (E + Q) seems to be a significant contributor to the hydrological mass balance during the time span from January 2005 to December 2010. Crowley et al. (2006) demonstrated, using GRACE-derived water storage changes and precipitation from both TRMM and the Climate Prediction Center’s (CPC) Merged Analysis of Precipitation (CMAP), that the Congo Basin tends to saturate at 30 to 40 mm of equivalent water storage over seasonal time scales. Disregarding the uncertainty in GRACE and TRMM products, it appears that the water storage becomes saturated due to precipitation influx in the Volta Basin at annual and semi-annual time scales at approximately 73 mm (Fig. 4).

The total de-trended output from the Volta Basin could then be determined as the right-hand side of Eq. (9) using GRACE-derived water storage changes and TRMM precipitation (GRACE-TRMM). This residual provides an estimate of the combined contribution of runoff plus the evaporation time series (Fig. 5). As the gridded runoff (surface and subsurface) and total evaporation simulated with the GLDAS (Rodell et al. 2004a) are available for the study period, we compared seasonal estimates of sink terms from GLDAS to those from GRACE and TRMM over the same time span (Fig. 5). Although GLDAS estimates have larger peak-to-peak amplitude than GRACE-TRMM-derived values, the temporal pattern of both time series is similar, with a phase lag of −0.28 ± 0.16 months (GRACE-TRMM precedes GLDAS).

In order to investigate the differences in these solutions, we computed the root mean square error (RMSE) value of the differences between the sink terms derived from GRACE-TRMM and GLDAS, which equal 20.2 mm/month (approximately 0.67 mm/d) with a correlation coefficient of 0.85. Our research only focused on sink terms (evaporation plus runoff), whereas it might be important to include runoff observations. If in situ runoff data were available, the methodology could be used to detect and examine changes in the evaporation pattern associated with the occurrence of extreme climatic events, and this will be a subject of future work. However, Cesanelli and Guarracino (2011) used an estimate of runoff as a fraction of the mean annual precipitation to compute the evaporation using GRACE with an RMSE of 22.6 mm/month (0.75 mm/d). They also reported an estimated RMSE value between GRACE and GLDAS of 25.0 mm/month (0.83 mm/d), which is in agreement with values reported by Rodell et al. (2004b), Ramillien et al. (2006), and Boronina and Ramillien (2008).

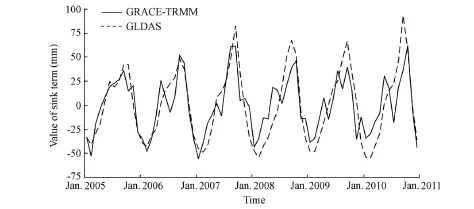
Fig. 5 Difference between time series of GRACE-TRMM-derived sink terms and sink terms from GLDAS

4 Conclusions

This study, for the first time, presents the seasonal variations of the differences between the precipitation from TRMM and the water storage variations from GRACE in the Volta Basin. Comparisons between estimates of evaporation plus runoff in the Volta Basin scale by GRACE-TRMM and GLDAS, which was considered independent data, showed good agreement, with an RMSE of 20.2 mm/month and a correlation coefficient of 0.85. This illustrates the ability of GRACE to predict hydrological processes, e.g., evaporation, on a regional scale in the Volta Basin. When constant and linear terms were removed, the time series of water storage changes estimated from GRACE exhibited a dominant annual signal of 129 mm peak-to-peak at the annual and semi-annual time scales (Fig. 4) for the period under consideration (from January 2005 to December 2010), which is equivalent to a water volume change of 52.51 km3. A comparison of this trend with accumulated precipitation showed a good qualitative agreement, with a phase difference of 0.42 ± 0.10 months. It also showed that the precipitation generally bounded the water storage change time series at seasonal time scales. This is the evidence of basin saturation at approximately 73 mm of equivalent water column and of the importance of sink terms (evaporation and runoff) to the hydrological balance.

References

Boronina, A., and Ramillien, G. 2008. Application of AVGRR imagery and GRACE measurements for calculation of actual evapotranspiration over the Quaternary aquifer (Lake Chad basin) and validation of groundwater models. Journal of Hydrology, 348(1-2), 98-109. [doi:10.1016/j.jhydrol.2007.09.061]

Cazenave, A., and Chen, J. 2010. Time-variable gravity from space and present-day mass redistribution in the Earth system. Earth and Planetary Science Letters, 298(3-4), 263-274. [doi:10.1016/j.epsl.2010.07.035]

Cesanelli, A., and Guarracino, L. 2011. Estimation of regional evapotranspiration in the extended Salado Basin (Argentina) from satellite gravity measurements. Hydrogeology Journal, 19(3), 629-639. [doi:10. 1007/s10040-011-0708-3]

Chen, J. L., Rodell, M., Wilson, C. R., and Famiglietti, J. S. 2005. Low degree spherical harmonic influences on Gravity Recovery and Climate Experiment (GRACE) water storage estimates. Geophysical Research Letters, 32(14), L14405. [doi:10.1029/2005GL022964]

Chen, J. L., Wilson, C. R., Tapley, B. D., and Grand, S. 2007. GRACE detects coseismic and postseismic deformation from the Sumatra-Andaman earthquake. Geophysical Research Letters, 34(13), L13302. [doi:10.1029/2007gl030356]

Chen, J. L., Wilson, C. R., Tapley, B. D., Longuevergne, L., Yang, Z. L., and Scanlon, B. R. 2010. Recent La Plata basin drought conditions observed by satellite gravimetry. Journal of Geophysical Research, 115(D22), D22108. [doi:10.1029/2010JD014689]

Cheng, M., and Tapley, B. D. 2004. Variations in the Earth’s oblateness during the past 28 years. Journal of Geophysical Research, 109(B9), B09402. [doi:10.1029/2004JB003028]

Crowley, J. W., Mitrovica J. X., and Bailey, R. C., Tamisiea, M. E., and Davis, J. L. 2006. Land water storage within the Congo Basin inferred from GRACE satellite gravity data. Geophysical Research Letters, 33(19), L19402. [doi:10.1029/2006GL027070]

Crowley, J. W., Mitrovica, J. X., and Bailey, R. C., Tamisiea, M. E., and Davis, J. L. 2007. Annual variations in water storage and precipitation in the Amazon Basin. Journal of Geodesy, 82(1), 9-13. [doi:10.1007/ s00190-007-0153-1]

Dahle, C., Flechtner, F., Gruber, C., König, D., König, R., Michalak, G., and Neumayer, K. H. 2012. GFZ GRACE Level-2 Processing Standards Document for Level-2 Product Release 0005. Potsdam: German Research Centre for Geosciences. [doi:10.2312/GFZ.b103-12020]

Deus, D., Gloaguen, R., and Krause, P. 2011. Water balance modelling in a semi-arid environment with limited in-situ data: Remote sensing coupled with satellite gravimetry, Lake Manyara, East African Rift, Tanzania. Hydrology and Earth System Sciences, 8(5), 8737-8792. [doi:10.5194/hessd-8-8737-2011]

Grippa, M., Kergoat, L., Frappart, F., Araud, Q., Boone, A., de Rosnay, P., Lemoine, J. M., Gascoin, S., Balsamo, G., Ottlé, C., et al. 2011. Land water storage variability over West Africa estimated by Gravity Recovery and Climate Experiment (GRACE) and land surface models. Water Resources Research, 47(5), 1-18. [doi:10.1029/2009WR008856]

Hinderer, J., Pfeffer, J., Boucher, M., Nahmani, S., Linage, C., Boy, J. P., Genthon, P., Seguis, L., Favreau, G., Bock, O., and Descloitres, M. 2011. Land water storage changes from ground and space geodesy: First results from the GHYRAF (Gravity and Hydrology in Africa) experiment. Pure and Applied Geophysics, 169(8), 1391-1410. [doi:10.1007/s00024-011-0417-9]

Kasei, R., Diekkrüger, B., and Leemhuis, C. 2010. Drought frequency in the Volta Basin of West Africa. Sustainability Science, 5(1), 89-97. [doi:10.1007/s11625-009-0101-5]

Kusche, J. 2007. Approximate decorrelation and non-isotropic smoothing of time-variable GRACE-type gravity field models. Journal of Geodesy, 81(11), 733-749. [doi:10.1007/s00190-007-0143-3]

Milzow, C., Krogh, P. E., and Bauer-Gottwein, P. 2011. Combining satellite radar altimetry, SAR surface soil moisture and GRACE total storage changes for hydrological model calibration in a large poorly gauged catchment. Hydrology and Earth System Sciences, 15(6), 1729-1743. [doi:10.5194/hess-15-1729-2011]

Ramillien, G., Frappart, F., Cazenave, A., and Güntner, A. 2005. Time variations of land water storage from an inversion of 2 years of GRACE geoids. Earth and Planetary Science Letters, 235(1-2), 283-301.[doi:10.1016/j.epsl.2005.04.005]

Ramillien, G., Frappart, F., Güntner, A., Ngo-Duc, T., Cazenave, A., and Laval, K. 2006. Time variations of the regional evapotranspiration rate from Gravity Recovery and Climate Experiment (GRACE) satellite gravimetry. Water Resources Research, 42(10), W10403. [doi:10.1029/2005WR004331]

Ramillien, G., Famiglietti, J. S., and Wahr, J. 2008. Detection of continental hydrology and glaciology signals from GRACE: A review. Surveys in Geophysics, 29(4-5), 361-374. [doi:10.1007/s10712-008- 9048-9]

Rodell, M., Houser, P. R., Jambor, U., Gottschalck, J., Mitchell, K., Meng, C. J., Arsenault, K., Cosgrove, B., Radakovich, J., Bosilovich, M., et al. 2004a. The global land data assimilation system. Bulletin of American Meteorological Society, 85(3), 381-394. [doi:10.1175/BAMS-85-3-381]

Rodell, M., Famiglietti, J. S., Chen, J., Seneviratne, S. I., Viterbo, P., Holl, S., and Wilson, C. R. 2004b. Basin scale estimates of evapotranspiration using GRACE and other observations. Geophysical Research Letters, 31(20), L20504. [doi:10.1029/2004gl020873]

Swenson, S., and Wahr, J. 2006. Post-processing removal of correlated errors in GRACE data. Geophysical Research Letters, 33(8), L08402. [doi:10.1029/2005gl025285]

Vey, S., Steffen, H., Müller, J., and Boike, J. 2012. Inter-annual water mass variations from GRACE in central Siberia. Journal of Geodesy, 287-299. [doi:10.1007/s00190-012-0597-9]

Wahr, J., Molenaar, M., and Bryan, F. 1998. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. Journal of Geophysical Research, 103(B12), 30205-30229. [doi:10.1029/98jb02844]

Wahr, J., Swenson, S., and Velicogna, I. 2006. The accuracy of GRACE mass estimates, Geophysical Research Letters, 33(6), L06401. [doi:10.1029/2005GL025305]

Werth, S., Güntner, A., Schmidt, R., and Kusche, J. 2009. Evaluation of GRACE filter tools from a hydrological perspective. Geophysical Journal International, 179(3), 1499-1515. [doi:10.1111/j.1365-246X.2009.04355.x]

Xie, H., Longuevergne, L., Ringler, C., and Scanlon, B. 2012. Calibration and evaluation of a semi-distributed watershed model of sub-Saharan Africa using GRACE data. Hydrology and Earth System Sciences Discussions, 9(2), 2071-2120. [doi:10.5194/hessd-9-2071-2012]

(Edited by Yun-li YU)

——

This work was supported by the Fundamental Research Funds for the Central Universities (Grant No. 2012B01314).

*Corresponding author (e-mail: vagnergf@hhu.edu.cn)

Received Dec. 10, 2012; accepted Apr. 5, 2013