大理岩破坏起裂应力及断裂能特征试验研究

张黎明，高 速，任明远，王在泉

（青岛理工大学a.理学院；b.蓝色经济区工程建设与安全山东省协同创新中心，山东 青岛 266033）

岩石的起裂应力是判断岩石类材料破坏征兆的重要指标之一。岩石破坏过程中线弹性变形阶段结束亦是裂纹扩展阶段的开始，中间的转折点即为起裂点。对于脆性材料在单轴和三轴压缩条件下的力学行为已经获得了较好的研究成果，对岩石的起裂、断裂特性也开展了相关的研究。

Gaziev等［1－2］发现岩石断裂能和起裂应力密切相关。黄达等［3］研究了加载速率与特征应力之间的对应关系。王学滨等［4］研究了单轴压缩破坏岩石试件断裂能的尺寸效应。徐松林等［5］提出大理岩三轴试验剪切断裂能的计算方法。杨圣奇等［6］研究了三轴压缩大理岩断裂能随围压的变化关系。朱泽奇等［7］研究了不同围下起裂应力、起裂角与围压的关系。Scott等［8］研究了岩石疲劳破坏过程中的应变能耗散特征。Xie等［9］基于能量释放和耗散原理研究了岩体破坏准则。

关于单轴加载条件下岩石破坏过程的能量演化规律已取得较多的研究成果，而三轴压缩破坏岩石的起裂应力是与围压密切相关的，目前这方面的研究还极为缺乏。本文对大理岩常规三轴压缩破坏过程的起裂应力和断裂能影响因素进行了研究。

1 试验介绍

试验采用三个批次的大理岩岩样分别进行单轴和常规三轴试验（岩样标号中字母前的数字表示岩样的1、2、3批次，字母T表示常规三轴压缩）。试验在MTS815岩石力学试验系统上进行，采用AE21C声发射设备检测声发射信息。试验全过程应力应变曲线（1T组）如图1所示。

2 岩石破坏断裂能计算方法

岩石受到外载荷作用发生破坏与能量的消耗有关［9］。外力对岩石做功先以能量积累为主，积累的能量达到一定值时就会发生耗散，岩样出现裂纹，并发展贯通，最终出现宏观的剪切滑移特征。确定了起裂应力就可以对岩石破坏进行提前预判。

岩石破坏与否与其应力状态密切相关，Gaziev等提出一种考虑3个主应力影响的强度指标，即将试验数据采用应力强度τi和应变强度εi2个指标进行分析处理［1－2］

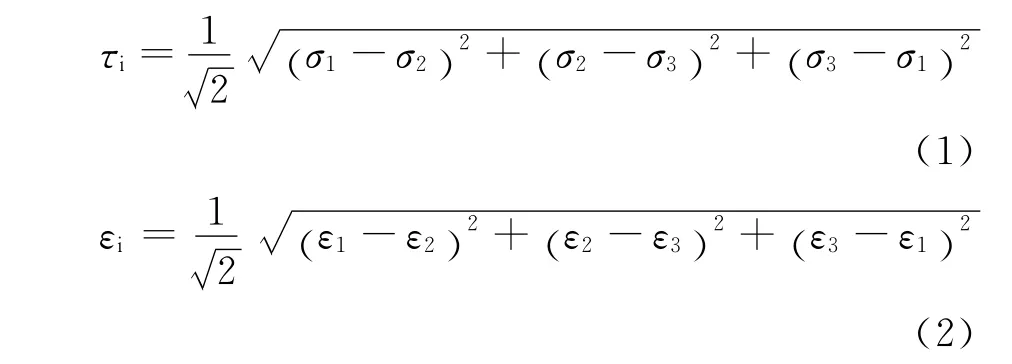
该强度指标能反映应力偏量第二不变量和应变张量对变形的影响，岩石裂纹出现时的τi即为起裂应力τci，相应的的能量计算式为

式中εci为τci所对应的εi。

常规三轴压缩试验τci的判断相对复杂，Gaziev等修正了考虑应力张量第一不变量和应力偏量第二不变量的起裂应力计算式［1－2］。

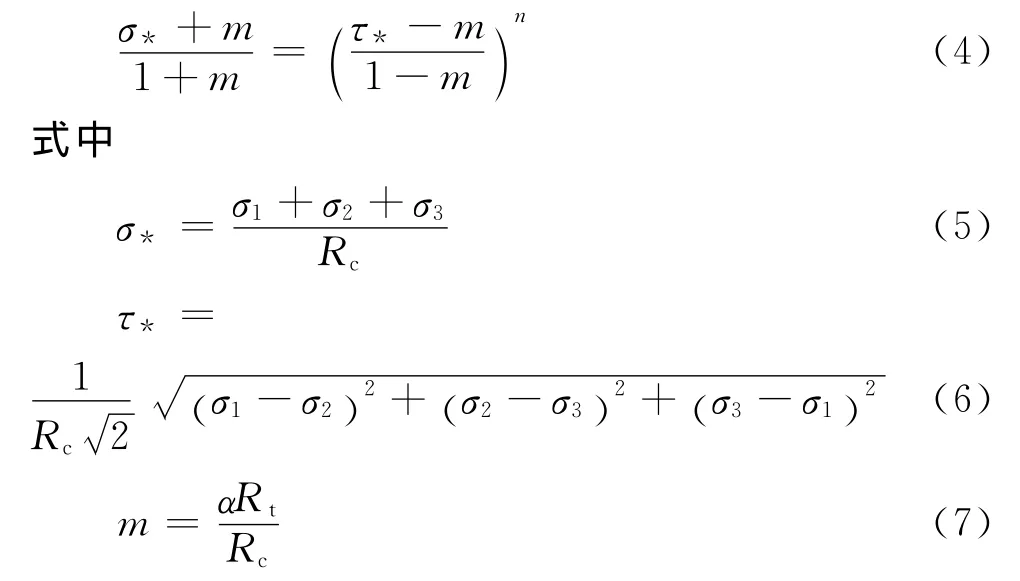
式中：Rt为抗拉强度；Rc为抗压强度；α为实常数；N为试验常数；可以用试验数据拟合得到。

对式（4）做线性变换可得

对岩样破坏时不同组合的主应力进行回归分析，如图2所示。最优的X和Y比例值为1.043 6。

将式（5）、（6）、（7）代入式（4），整理化简后可得

当τi／τi＊＝1时，表示裂纹开始扩展，此时对应的应力即为岩石的起裂应力τci。随后τi会继续增大，岩样的裂纹将扩展、贯通，并逐步形成宏观的剪切滑移面。为了判断岩样裂纹开始扩展的位置，需要确定计算式（3）中的积分上限εci。

表1给出了围压30 MPa岩样破坏过程的起裂应力判断方法。首先根据式（1）和式（10）进行计算得到τi和τi＊，根据τi／τi＊的比值判断起裂应力位置。当τi／τi＊＝1.002时，最接近1，确定大理岩起裂应力为σ1ci＝114.88 MPa，对应的ε1ci＝0.002 32，ε2ci＝ε3ci＝－0.000 26。根据式（1）、式（2）得εci＝0.002 58，τci＝84.883 MPa，根据式（3）得起裂断裂能Eci＝101.14 kJ／m3。岩样到达峰值强度前τi／τi＊比值不断增大，到峰值强度是达到1.253，峰值强度之后τi／τi＊比值逐渐减小。

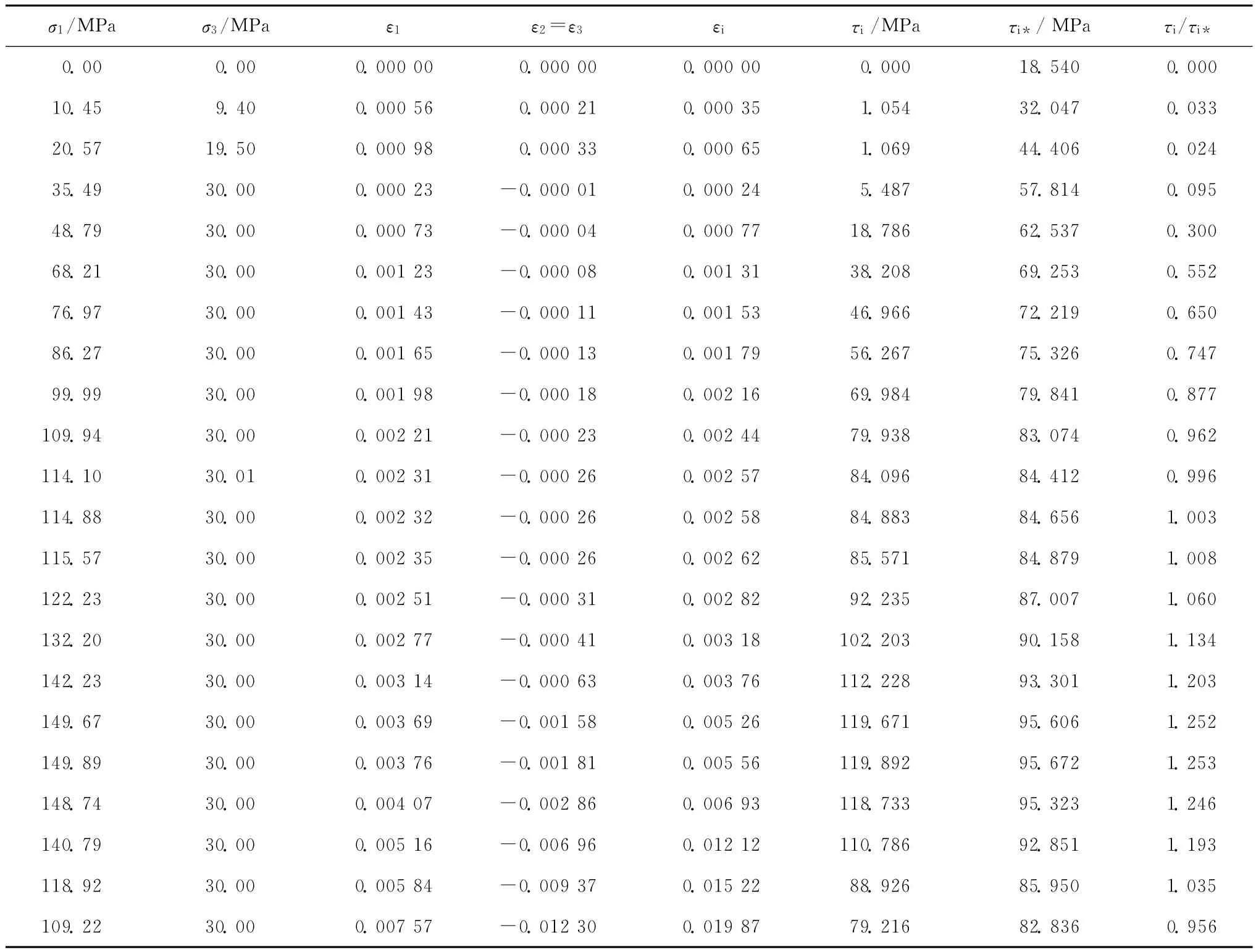
表1 大理岩常规三轴加荷试验数据（1T03＃）

3 大理岩起裂应力和断裂能分析

3.1 大理岩起裂应力分析

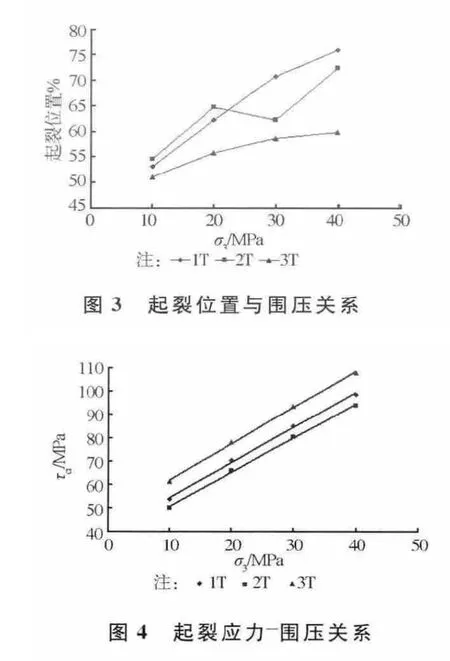
表2为大理岩常规三轴加荷破坏数据分析表。常规三轴加荷破坏大理岩起裂应力基本位于峰值强度的50%～70%之间。从图3起裂应力与围压的关系曲线可以看出，起裂应力与围压密切相关，随围压升高起裂应力逐渐增加（2T组30 MPa岩样出现小的波动），并且随围压升高向峰值强度逐渐靠近。以1T组为例，围压增加，岩样对应的起裂应力分别为53.6、70.3、84.9和98.5 MPa，对应的峰值强度比例分别为53%、62%、71%和76%。

图4为3批岩样起裂应力和围压拟合曲线，相关系数都大于90%，τci和围压σ3满足线性关系

τci＝Mσ3＋N（11）

式中：M、N为材料参数。

表2 常规三轴破坏试验数据分析

3.2 起裂断裂能特征分析

从表2看到，岩样的起裂断裂能随围压升高有递增趋势。分别对3组试验数据进行回归分析，如图5所示，起裂断裂能Eci和围压σ3满足线性关系

式中：H、I为材料参数。

图6为起裂断裂能和峰值应力关系，关系式为

相关系数为94%。对于试验范围内的大理岩，岩样断裂所需要的能量与岩样破坏时的轴向应力呈线性关系，岩石强度越高，起裂断裂能就越大。

4 大理岩破坏过程声发射特征分析

图7为常规三轴（围压20 MPa）岩样破坏全过程的振铃计数率时间关系曲线。声发射从另一方面表征岩石的裂纹扩展过程。声发射振铃计数率在线弹性变形阶段末期出现突增，此后振铃计数率值开始增加，最大振铃计数率出现在峰值附近。由于围压的存在，峰值强度后的应力跌落阶段较缓慢。时间关系曲线。试验过程中声发射事件数随着围压的增加逐渐增多，声发射能量计数率的第一次突增出现在弹性变形阶段的末端（图8（a）中应力

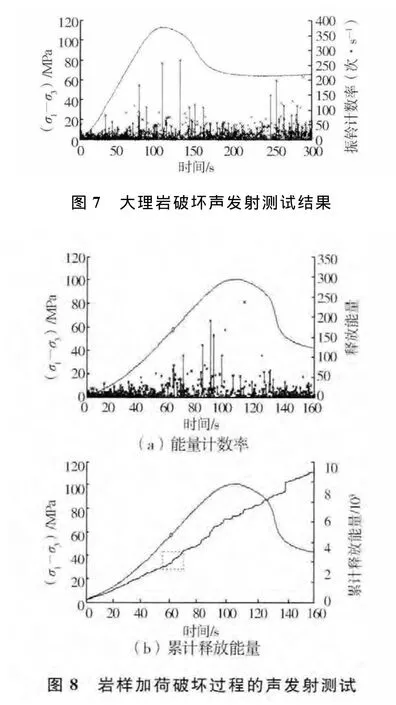
如图8为1T组岩样10 MPa围压作用下的应力差 能量计数率时间曲线上标注的点），该位置与理论计算确定的起裂位置相对应。起裂应力对应的声发射能量计数出现突跳，而且起裂点之后能量计数率明显增加速度明显变快。图8（b）中的累计释放能量曲线表明，在起裂点之前累计释放能量基本呈线性增加，在起裂点位置累计释放能量出现了1个小的突跳，随后累计释放能量基本成跳跃式增加，但突跳的值略有变化。理论计算求得的起裂点和声发射监测数据确定的起裂位置吻合较好。

5 Mogi-Coulomb强度准则

考虑到中间主应力的对岩石强度影响，Mogi将Mohr-Coulomb强度准则进行了改进［10］，对常规三轴试验而言，其数学形式为

式中：A、B为试验材料参数；c为黏聚力；φ为内摩擦角。根据式（13）对试验数据回归如图9。

根据 Mogi-Coulomb准则得到c＝23 MPa，φ＝29°，即破裂面的法向与岩样轴向的夹角为α＝59.5°。常规三轴压缩（围压20 MPa和40 MPa）的岩样，岩样α角测量值分别为58.2°和57.8°，理论值与试验值吻合较好。

6 结 论

1）大理岩起裂应力随围压升高向峰值点靠近，起裂位置位于峰值强度的53%～76%之间，起裂断裂能随着围压升高逐渐增加。

2）声发射能量计数率在起裂位置有明显的突跳，而且起裂点之后能量计数率增加速度变快。理论计算的起裂应力和声发射监测数据吻合较好。

3）Mogi-Coulomb强度准则确定的破裂面倾角与试验实测值吻合较好。

［1］Gaziev E，Levtchouk V.Strength characterization for rock under multiaxial stress states ［C］／／9th International Congress on Rock Mechanics，Paris，France.1999.

［2］Gaziev E.Rupture energy evaluation for brittle materials［J］.International Journal of Solids and Structures，2001，38：7681-7690.

［3］黄达，黄润秋，张永兴.粗晶大理岩单轴压缩力学特性的静态加载速率效应及能量机制试验研究［J］.岩石力学与工程学报，2012，31（2）：245-255.

Huang D，Huang R Q，Zhang Y X.Experimental investigations on static loading rate effects on mechanical properties and energy mechanism of coarse crystal grain marble under uniaxial compression ［J］.Chinese Journal of Rock Mechanics and Engineering，2012，31（2）：245-255.

［4］王学滨.岩样单轴压缩塑性变形及断裂能研究［J］.岩石力学与工程学报，2005，24（10）：1735-1739.

Wang X B.Analysis of plastic deformation and fracture energy of rock specimen in uniaxial compression ［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24（10）：1735-1739.

［5］徐松林，吴文，王广印，等.大理岩等围压三轴压缩全过程研究II：剪切断裂能分析［J］.岩石力学与工程学报，2002，21（1）：65-69.

Xu S L，Wu W，Wang G Y，et al.Study on complete procedures of marble under triaxial compression II：Analysis of shear fracture energy［J］.Chinese Journal of Rock Mechanics and Engineering，2002，21（1）：65-69.

［6］杨圣奇，徐卫亚，苏承东.大理岩三轴压缩变形破坏与能量特征研究［J］.工程力学，2007，24（1）：136-141.

Yang S Q，Xu W Y，Su C D.Study of deformation failure and energy properties of marble specimen under triaxial compression［J］.Engineering Mechanics，2007，24（1）：136-141.

［7］朱泽奇，盛谦，冷先伦，等.三峡花岗岩起裂机制研究［J］.岩石力学与工程学报，2007，26（12）：2570-2575.

Zhu Z Q，Sheng Q，Leng X L，et al.Study of crack initiation mechanism of Three Gorges granite ［J］.Chinese Journal of Rock Mechanics and Engineering，2007，26（12）：2570-2575.

［8］Scott O E，George T J，Cross C J，et al.Analysis of strain energy behavior throughout a fatigue process［J］.Experimental Mechanics，2011，51（8）：1317-1323.

［9］Xie H P，Li L Y，Peng R D，et al.Energy analysis and criteria for structural failure of rocks［J］.Journal of Rock Mechanics and Geotechnical Engineering，2009，1（1）：11-20.

［10］Pariseau W G.Fitting failure criteria to laboratory strength tests ［J］.International Journal of Rock Mechanics and Mining Sciences，2007，44（4）：637-646.

（编辑胡 玲）