边坡动力破坏机理的振动台试验研究

刘振平，刘福海，赵显波

（1.黑龙江工程学院 土木与建筑工程学院，哈尔滨 150050；

2.东北电力设计院，长春130021；3.黑龙江省水利科学研究院，哈尔滨 150080）

在土木工程和水利工程中，有众多的自然边坡、人工边坡如堤坝、路基路堑等边坡工程。中国的许多重大工程如大型水电站、南水北调西线工程、西部山区高速公路等均处于强震区，特别是2008年汶川“5·12”地震以来，边坡动力破坏机理引起学者们的广泛关注，成为岩土地震工程领域中重要的研究课题之一。有关边坡地震的原型观测资料很少，所以室内振动台试验就成为研究地震作用下边坡动力问题的重要手段之一。Lin等［1］采用大型振动台试验研究土坡在地震作用下的响应，认为砂土边坡破坏面较浅，只是坡体表面的破坏。徐光兴等［2－3］通过振动台模型试验研究了混合土边坡的动力特性，并结合数值分析结果认为在强震作用下单一均质土层边坡的破坏模式仍然是沿着某一弧形潜在滑动面失稳。许强等［4］通过多组振动台试验认为均质土坡和块状岩质斜坡的动力破坏模式都是坡顶拉裂，中下部剪切滑移破坏。陈新民等［5－6］采用振动台试验研究了粘土边坡动力特性、动力反应和宏观变形，发现在动力作用下边坡坡顶和坡脚出现裂缝。叶海林等［7］岩质边坡大型振动台模型试验，结果表明地震滑动面为上部拉裂缝和下部剪切滑移面形成贯通的破裂面。刘君等［8］把PIV技术应用在土质边坡振动台模型试验中，获取了边坡破坏的完整过程。Wang等［9］在砂土边坡振动台试验中采用PIV技术获取了边坡表面的位移场，探讨了边坡动力失稳机理。Wartman等［10－11］通过多组粘土边坡振动台模型试验研究了边坡产生的永久位移，并与基于峰值和残余强度的Newmark公式计算结果进行了比较。Katz等［12］采用振动沙箱研究了砂土边坡破坏的类型和频率的关系。以上针对边坡的动力特性、宏观破坏现象及个别点的位移进行的研究，而没有涉及边坡的位移场，刘君、Wang等虽用PIV技术得到了整个边坡的位移场，但没有对应变场进行研究。

应变是直接对含有噪声的离散位移进行差分计算得到的，那么即使微小的位移测量误差也会被急剧地放大，使计算的应变不可靠［13］。一般的数据拟合平滑方法也不能满足应变计算的精度要求，潘兵等［13－14］提出了局部最小二乘拟合的应变计算方法，其原理同Savitzky-Golay平滑方法。该方法能够在一定程度上去除原始位移场的噪声，缺点是由于每个位移点都要一个计算窗口平滑，计算量巨大，并且对于非均匀应变场，应变计算窗口的大小显著影响应变的计算精度，目前还没有合适的方法来选择最佳的窗口大小。本文采用数字图像位移和有限元数据平滑技术，得到了整个边坡模型的位移场和应变场，同时探讨了土质边坡的地震破坏机理。

1 基于有限元数据平滑的应变计算

数字图像位移测量技术现在已经成熟，采用互相关图像匹配技术获取位移场后，再用有限元数据平滑方法对位移场进行处理后，得到应变场。

1.1 基本原理

基本思路是引入泛函f（F）［15－19］，使该泛函取得极小值的自变函数F就是要求的光滑位移函数。

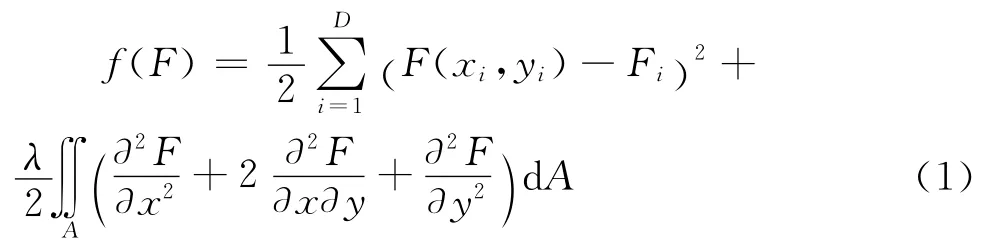
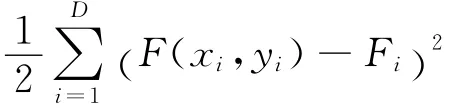
根据试验数据点的位置分布，把区域A划分为若干单元，在每一个单元内用形函数逼近光滑函数F，这个过程与有限元方法是一样的。

在第j个单元内，把光滑函数F表示成式中：N j为第j个单元的形函数；uej为第j个单元的节点自由度。

式（9）是有限元的标准格式，其中K＝K1＋λK2，λ是平滑系数，U表示所有单元的节点自由度。平滑系数的确定方法在下文专门论述。

只要确定了平滑系数，就可从式（9）中解出U，再从式（2）中得到平滑位移函数u，其应变的计算方法如下：

有限变形条形下的格林（Green）应变［20］（以受压为正）为

式中：u和v分别为上述所求的x和y方向的位移函数；εx和εy分别为x和y方向的正应变；γxy为工程剪应变；γmax为最大剪应变。

小变形条件下柯西（Cauchy）应变的计算可不考虑上述应变表达式中的二次项。

1.2 形函数的确定

采用三角形单元，以便适应任意形状的数据区域。同时为提高插值函数的光滑可导性，采用的是五次多项式的单元插值函数［15］，其表达式为式中：X为变量项；C为系数列向量。由于沿三角形单元三条边满足法向导数连续的条件，21个系数可缩减为18个。

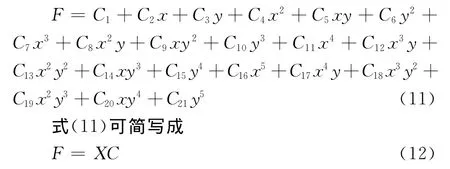
1.3 平滑系数的确定

为了能够自动得到最佳的平滑系数，Golub等［21］、Craven等［22］及 Bates等［23］提 出 了 广 义 交 互验证GCV方法，建立了关于λ的GCV函数X是n阶满秩阵，K2是奇异阵，其秩为r。拟总体刚度阵K1是对称正定阵，因此式（15）成立，可以证明X是满秩阵，因此y也能够由式（16）式唯一确定。

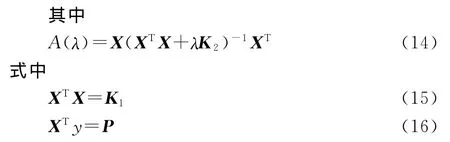
求取广义交互验证函数GCV的最小值，就可以得到最佳平滑系数λ，具体计算方法详见文献［24］。

2 试验设备及模型设计

2.1 试验设备

试验在大连理工大学工程抗震试验室的水平与竖直双向水下振动台上进行，其主要性能参数如下：数字式控制方式，台面尺寸3 m×4 m，最大载重100 k N，工作频率0.1～50 Hz；满载工况下最大加速度±1.0g（水 平 向）、±0.7g（竖 向）、最 大 速 度±50 cm／s（水平向）、±35 cm／s（竖向）、最大位移±75 mm（水平向）、±50 mm（竖向）。

2.2 试验模型

在钢制模型箱内堆制模型进行试验，为便于观察和图像采集，一侧为有机玻璃。模型坝坝高1.3 m，边坡坡率1∶1.6，其模型如图1所示。模型填土基本性能参数见表1。

表1 试验填土基本性能参数

图1 边坡振动台模型示意图（单位：cm）

试验加载的是频率10 Hz的正弦增幅波（喇叭波），如图2所示。从0开始逐渐增加，直至边坡完全失稳。

采用的图像采集设备是CANON EOS 450D高清数码相机，最大分辨率4 272×2 848像素，配备10～22 mm广角镜头，可以在距模型2 m处拍摄整个模型的图片。存储为JPG格式的图片文件，最大连拍速度约3.3帧／s。振动过程中连续的采集图像，用于数字图像位移和应变识别。

图2 输入的加速度时程

3 试验结果分析

3.1 模型的位移应变计算流程

开发了一套数字图像测量分析程序，可以批处理多种格式的图片，可以得到一系列的位移场和应变场，还能以等值线图、云图和矢量图等形式输出各种位移场、应变场和速度场。其计算流程和步骤如下：

位移计算流程：图像像素块划分→计算总位移→计算模型箱位移→计算相对位移（总位移减去模型箱刚体位移）→删除计算的位移坏点→输出位移场等后处理。

得到位移场后，用有限元平滑位移场再微分计算应变场。其计算流程如下：生成单元和节点信息→计算单元刚度阵和单元节点荷载列阵→集成总体刚度阵和总体节点荷载列阵→计算平滑系数→求解节点未知参数→平滑位移场微分求应变→输出应变场等后处理。

3.2 边坡模型的破坏过程描述

边坡模型破坏过程基本可分3个阶段，第1阶段是整体变形阶段（图3（a）），当输入加速度较小时，整个模型以均匀沉降变形为主，同时伴有相对于模型箱的水平往复运动；第2阶段是滑移变形阶段（图3（b）），当输入加速度大约在0.1g时，模型开始沿边坡一侧向下滑移，随着输入加速度的增大，滑移量也逐渐增大，在输入加速度在0.45g时，坡顶出现张拉裂缝，坡体内部也出现剪切裂隙，形成明显的滑动带，边坡达到极限破坏状态；第3阶段是破坏阶段，滑动带上的裂隙使得滑动体与边坡相对分离，滑动体加速下滑，最后整个坡体坍塌，边坡完全破坏。

从图3（c）可以看出，边坡模型动力失稳存在深层滑动带，滑动面大概呈圆弧状。

3.3 位移分析

图4、图5和图6分别是8.42 s（对应输入加速度为0.45g）时即在极限破坏状态时的水平位移、竖向位移和总位移的等值线图，其水平位移出现在坡面中部，竖向位移在坡顶附近，水平位移和总位移等值线基本平行于坡面，均符合一般的边坡破坏时的位移分布规律。

图3 边坡模型位移矢量

图4 8.42 s时（输入加速度0.45 g）时水平位移场（单位：mm）

图5 8.42 s时（输入加速度0.45 g）时竖向位移场（单位：mm）

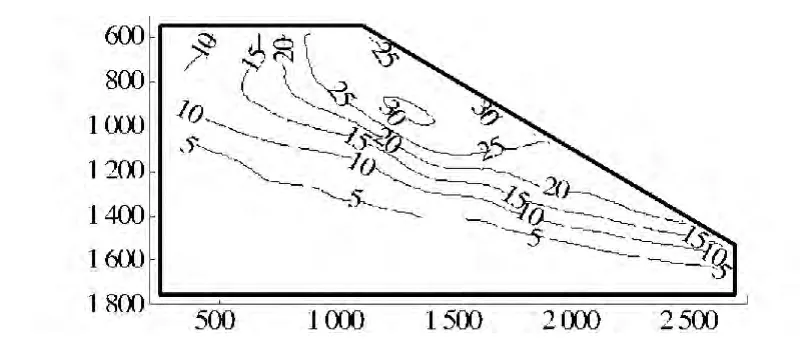
图6 8.42 s时（输入加速度0.45 g）时总位移场（单位：mm）

3.4 应变分析

从图7和图8最大剪应变和水平方向应变分布上可以看出，坡体中部到坡脚是剪切破坏，坡顶一定深度是拉剪破坏。其变形破坏模式与汶川地震观察到的边坡破坏现象相吻合［25］：土坡主要是坡顶向下一定深度内的拉破坏，坡脚向上延伸形成剪切滑移带，最终二者连通形成贯通的破裂面。这也与许强等［4］的振动台试验结果以及郑颖人等［26－27］用 FLAC程序做的数值分析结果基本一致。

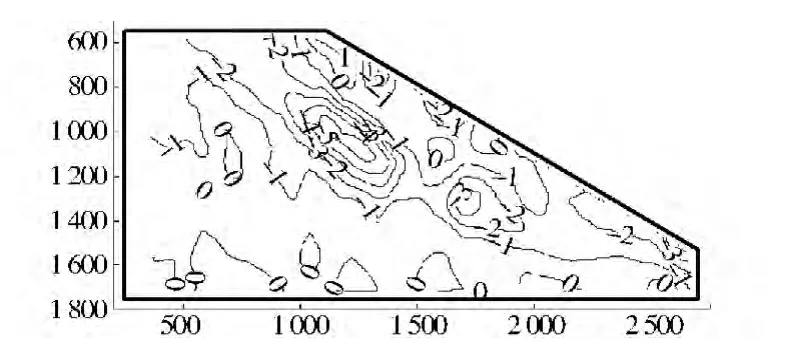
图7 8.42 s时（输入加速度0.45 g）时水平应变场（单位：%）

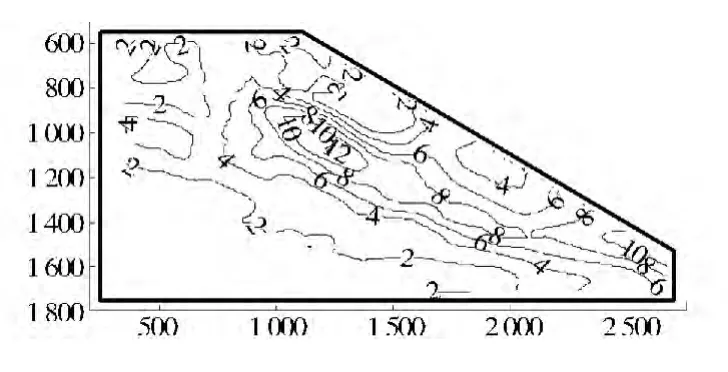
8 8.42 s时（输入加速度0.45 g）时最大剪应变场（单位：%）

3.5 位移应变时程分析

A点位于滑动体上，B点位于滑动体外（图1），从图9的位移时程可以看出，位移随时间是逐渐增加的，没有明显的突变点，说明边坡在地震作用下是渐进式破坏的。

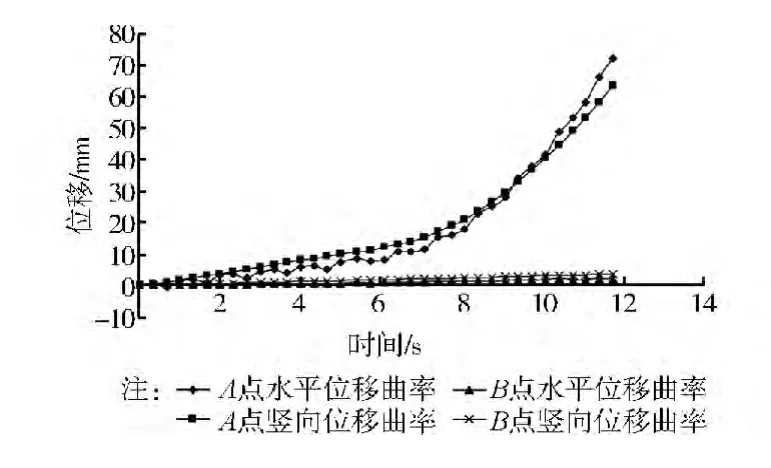
图9 位移时程曲线

由于位移时程曲线没有明显的突变拐点，如何判断模型破坏的时刻就成为一个难题。地震作用下边坡形成滑移带后，滑动体与坡体相对分离，由于滑移带的阻隔，滑动体以外的坝体振动对其影响将大大减小，滑动体将比较平稳的运动，而不会随输入地震波而振动。所以可以把位移时程曲线的曲率做为判断坝坡失稳滑移的一个物理量，这里所指的曲率是有正负之分的，正号表示是凹曲线，负号表示是凸曲线，可定义为广义曲率。

式中：κ为广义曲率；y′是位移的一阶导数；y″是位移的二阶导数。

从A点的位移时程曲线曲率（图10）可以看出，在8.42 s之前，曲率以零线为中心上下波动，说明在此之前没有发生连续的滑动，而在此之后，曲率迅速趋于零，不再发生波动，该点此时已经失稳破坏，曲率发生突变表明滑移带已经贯通形成，边坡整体失稳，达到了极限抗震状态。位于滑动体以外的B点，曲率自始自终都处于振动状态，没有发生失稳破坏。由此可知，用位移时程曲线曲率做为判断边坡动力破坏的物理量是可行的。

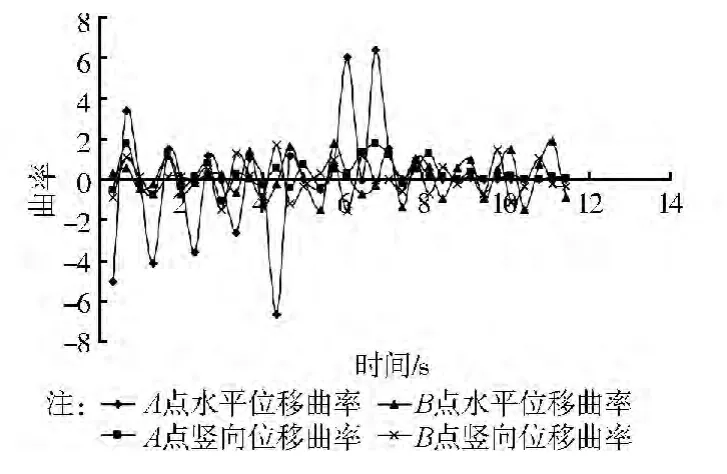
图10 位移时程曲线的曲率

4 结 论

将有限元数据平滑方法引入到数字图像位移应变测量中是可行的，得到了边坡振动台模型整个试验过程的位移场和应变场。初步表明土质边坡的变形是渐进式的，坡体中部到坡脚是剪切破坏，坡顶一定深度是拉剪破坏，破坏时有深层的圆弧状滑动面，用位移时程的广义曲率做为判断边坡动力破坏的物理量是可行的。

［1］Lin M L，Wang K L.Seismic slope behavior in a largescale shaking table model test ［J］.Engineering Geology，2006，86（2／3）：118-133.

［2］徐光兴，姚令侃，高召宁，等.边坡动力特性与动力响应的大型振动台模型试验研究［J］.岩石力学与工程学报，2008，27（3）：624-631.

Xu G X，Yao L K，Gao Z N，et al.Large-scale shaking table model test study on dynamic characteristics and dynamic responses of slope［J］.Chinese Journal of Rock Mechanics and Engineering，2008，27（3）：624-631.

［3］徐光兴，姚令侃，李朝红，等.边坡地震动力响应规律及地震动参数研究［J］.岩土工程学报，2008，30（6）：918-923.

Xu G X，Yao L K，Li C G，et al.Dynamic response of slopes under earthquakes and influence of ground motion parameters［J］.Chinese Journal of Geotechnical Engineering，2008，30（6）：918-923.

［4］许强，陈建君，冯文凯，等.斜坡地震响应的物理模拟试验研究［J］.四川大学学报：工程科学版，2009，41（3）：266-272.

Xu J，Chen J J，Feng W K，et al.Study of the seismic response of slopes by physical modeling ［J］.Journal of Sichuan University：Engineering Science Edition，2009，41（3）：266-272.

［5］陈新民，沈建，魏平，等.下蜀土边坡地震稳定性的大型振动台试验研究（I）-模型试验设计［J］.防灾减灾工程学报，2010，30（5）：492-502.

Chen X M，Shen J，Wei P，et al.Large-scale shaking table test of seismic stability of Xiashu loess slopes（I）：design of model test［J］.Journal of Disaster Prevention and Mitigation Engineering，2010，30（5）：492-502.

［6］陈新民，沈建，魏平，等.下蜀土边坡地震稳定性的大型振动台试验研究（II）-试验结果及分析［J］.防灾减灾工程学报，2010，30（6）：587-594.

Chen X M，Shen J，Wei P，et al.Large-scale shaking table test of seismic stability of Xiashu loess slopes（II）：analysis of test results ［J］.Journal of Disaster Prevention and Mitigation Engineering，2010，30（6）：587-594.

［7］叶海林，郑颖人，杜修力，等.边坡动力破坏特征的振动台模型试验与数值分析［J］.土木工程学报，2012，45（9）：128-135.

Ye H L，Zheng Y R，Du X L，et al.Shaking table model test and numerical analysis on dynamicfailure characteristics of slope［J］.China Civil Engineering Journal，2012，45（9）：128-135.

［8］刘君，刘福海，孔宪京，等.PIV技术在大型振动台模型试验中的应用［J］.岩土工程学报，2010，32（3）：368-374.

Liu J，Liu F H，Kong X J，et al.Application of PIV in largescale shaking table model tests ［J］.Chinese Journal of Geotechnical Engineering，2010，32（3）：368-374.

［9］Wang K L，Lin M L.Initiation and displacement of landslide induced by earthquake-a study of shakingtable model slope test［J］.Engineering Geology，2011，122：106-114.

［10］Wartman J.Physical model studies of seismically induced deformations in slopes ［D］.California：University of California-Berkeley，1999.

［11］Wartman J，Seed R B，Bray J D.Shaking table modeling of seismically induced deformations in slopes ［J］.Journal of Geotechnical and Geoenvironmental Engineering，2005，131（5）：610-622.

［12］Katz O，Aharonov E.Andslides in vibrating sand box：what controls types of slope failure and frequencymagnitude relations？［J］.Earth and Planetary Science Letters，2006，247（3）：280-294.

［13］潘兵，谢惠民.数字图像相关中基于位移场局部最小二乘拟合的全场应变测量［J］.光学学报，2007，27（11）：1980-1986.

Pan B，Xie H M.Full-field strain measurement based on least-square fitting of local displacement for digital image correlation method［J］.Acta Optica Sinica，2007，27（11）：1980-1986.

［14］Pan B，Xie H M，Guo Z Q，et al.Full-field strain measurement using a two-dimensional Savitzky-Golay digital differentiator in digital image correlation ［J］.Optical Engineering，2007，46（3）：1-10.

［15］Segalman D J，Woyak D B，Rowlands R E.Smooth spline-like finite-element differentiation of full-field experimental data over arbitrary geometry ［J］.Experimental Mechanics，1979，19（12）：429-437.

［16］Engelstad M J，Chambless D A，Swinson W F，et al.Hybrid stress analysis of vibrating plates using holographic interferometry and finite elements ［J］.Experimental Mechanics，1987，27（1）：23-30.

［17］Feng Z，Rowlands R E.Continuous full-field representation and differentiation of three-dimensional experimental vector data［J］.Computers and Structures，1987，26（6）：979-990.

［18］Sutton M A，Turner J L，Burck H A，et al.Full-field repersentation of discretely smapled surface deformational for displacement and strain analysis ［J］.Experimental Mechnaics，1991，31（2）：168-177.

［19］Freese C E，Gee L.A multilevel treatment of moiré fringe data using finite elements ［J］.Experimental Mechanics，1999，39（4）：304-310.

［20］陆明万，罗学富.弹性理论基础［M］.北京：清华大学出版社，2001：38-43.

［21］Golub G H，Heath M，Wahba G.Generalized cross validation as a method for choosing a good ridge parameter［J］.Technometrics，1979，21（2）：215-223.

［22］Craven P，Wahba G.Smoothing noisy data with spline functions：estimating the correct degree of smoothing by the method of generalized cross-validation ［J］.Numerische Mathematik，1979，31：377-403.

［23］Bates D M，Lindstrom M J，Wahba G，et al.Gcvpak-routines for generalized cross validation ［J］.Communications in Statistics-Simulation and Computation，1987，16（1）：263-297.

［24］Kent J T，Mohammadzadeh M.Global optimization of the generalized cross-validation criterion ［J］.Statistics and Computing，2000，10（3）：231-236.

［25］许强，董秀军.汶川地震大型滑坡成因模式［J］.中国地质大学学报：地球科学，2011，36（6）：1134-1142.

Xu J，Dong X J.Genetic types of large-scale landslides induced by Wenchuan Earthquake［J］.Journal of China University of Geosciences：Earth Science，2011，36（6）：1134-1142.

［26］郑颖人，叶海林，黄润秋.地震边坡破坏机制及其破裂面的分析探讨［J］.岩石力学与工程学报，2009，28（8）：1714-1723.

Zheng Y R，Ye H L，Huang R Q.Analysis and discussion of failure mechanism and fracture surface of slope under earthquake ［J］.Chinese Journal of Rock Mechanics and Engineering，2009，28（8）：1714-1723.

［27］郑颖人，叶海林，黄润秋，等.边坡地震稳定性分析探讨［J］.地震工程与工程振动，2010，30（2）：173-180.

Zheng Y R，Ye H L，Huang R Q，et al.Study on the seismic stability analysis of a slope ［J］.Journal of Earthquake Engineering and Engineering Vibration，2010，30（2）：173-180.

（编辑王秀玲）