客货共线大跨度简支钢桁梁桥梁轨相互作用*
于向东,沙 嵩,闫 斌
(中南大学 土木工程学院,湖南 长沙 410075)
客货共线大跨度简支钢桁梁桥梁轨相互作用*
于向东†,沙 嵩,闫 斌
(中南大学 土木工程学院,湖南 长沙 410075)
以黄韩侯铁路上某156m大跨度简支钢桁梁桥为背景,采用理想弹塑性道床阻力模型,建立了轨-梁-墩一体化空间有限元模型,对钢桁梁桥上钢轨伸缩力、挠曲力、制动力以及断轨力分布规律进行了分析,探讨了相邻简支梁支座布置、桥墩顶纵向刚度、小阻力扣件布置等设计参数对钢轨纵向力的影响.研究表明:钢轨伸缩力为主要控制性荷载;相邻简支梁宜采用与钢桁梁相同方向的支座布置方式;随墩顶刚度的增加,钢桁梁桥上钢轨伸缩力和挠曲力增大,制动力减小;在钢桁梁桥上采用小阻力扣件即可以减小约36%的钢轨伸缩力.
线路工程;铁路桥梁;钢梁桥;梁轨相互作用;钢轨纵向力;设计参数
铁路桥梁与轨道相互作用问题一方面影响轨道布置,另一方面影响桥跨布置和下部结构刚度[1],研究该课题具有重要意义.国内外学者已对混凝土简支梁桥、连续梁桥和斜拉桥的梁轨相互作用进行了广泛研究[2-10],如卜一之提出了高速铁路有砟线路与桥梁相互作用宜采用理想弹塑性阻力模型,并采用了非线性连杆模拟道砟层[5];徐庆元建立了能够考虑单、双线制动的三维实体单元有限元模型,探讨了不同因素对混凝土简支梁和连续梁桥线路纵向力传递的影响[6-7];闫斌采用带刚臂的梁单元模拟斜拉桥主梁、非线性杆单元模拟线路阻力,分析了相邻桥跨和钢轨伸缩调节器对斜拉桥上无缝线路纵向力的影响[8-9];朱彬对钢箱混合斜拉桥无缝线路纵向力进行了分析,并讨论了小阻力扣件和钢轨伸缩调节器的布置方案[10].
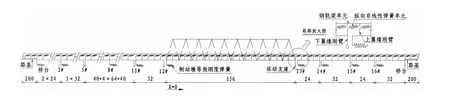
图1 有限元模型及桥跨布置(单位:m)Fig.1 Finite element model and arrangement of bridge spans(unit:m)
但对大跨度简支钢桁梁桥上无缝线路纵向力分布特点的相关研究较少,相邻不等跨度桥梁对大跨度钢桁梁桥上无缝线路纵向力的影响也不明确.简支钢桁梁桥具有跨度大、自重轻、受力明确、施工周期短等优点,近年来使用日益广泛.因此,有必要对大跨度简支钢桁梁桥与轨道相互作用进行研究.本文以黄韩侯铁路线上某156m简支钢桁梁桥为研究背景,建立了考虑轨道、相邻桥跨、路基、墩台的钢桁梁桥与有砟轨道相互作用有限元模型,探讨了大跨度钢桁梁桥上无缝线路纵向力的分布规律,研究了相邻简支梁支座布置、桥墩顶纵向刚度、小阻力扣件布置方式等设计参数对于梁轨相互作用的影响.
1 梁轨计算模型与参数
本工程位于黄韩侯铁路线(客货共线铁路)上,大桥孔跨布置为2×24m简支T梁+3×32m简支T梁+ (40+4×64+40)m混凝土连续梁+32 m简支T梁+156m钢桁梁+24m简支T梁+32 m简支T梁+24m简支T梁+32m简支T梁.其中钢桁梁桁高17m,桁宽8.6m,纵梁设置2处断开,桥上铺设单线有砟轨道,轨道采用60kg/m的钢轨.
本文在既有研究成果的基础上,采用带竖向刚臂的梁单元模拟桥梁,用非线性弹簧模拟梁轨之间纵向连接,建立的有限元模型如图1所示.
桥墩顶纵向刚度取1 000kN/cm,桥台顶纵向刚度取1 500kN/cm.为准确模拟边界条件,在桥梁范围外的路基上模拟(L+40m)长度(L为桥孔平均长度)的钢轨[11],此处取200m.线路纵向阻力模型采用《铁路无缝线路设计规范》[12]中的理想弹塑性模型,即认为梁轨相对纵向位移超过2mm(0.5 mm)时,轨道将发生滑移.道床纵向阻力:


式中:r为线路纵向阻力,(kN/m)/轨;u为梁轨纵向相对位移,mm.
计算钢轨伸缩力时,不考虑梁温升降的交替变化,因此本文只计算钢桁梁升温25℃,混凝土梁升温15 ℃的工况[12].
计算钢轨挠曲力时,采用中-活载,分机车下和车辆下两段等效均布加载于纵梁单元上(加载长度为200m).简支梁计算挠曲力时可简化为在相邻两孔梁上布载,连续梁在固定支座至梁端的多跨梁上布载[12],针对本桥,将活载简化为4种最不利方式进行加载(见图2),计算时取4种工况下的包络值.
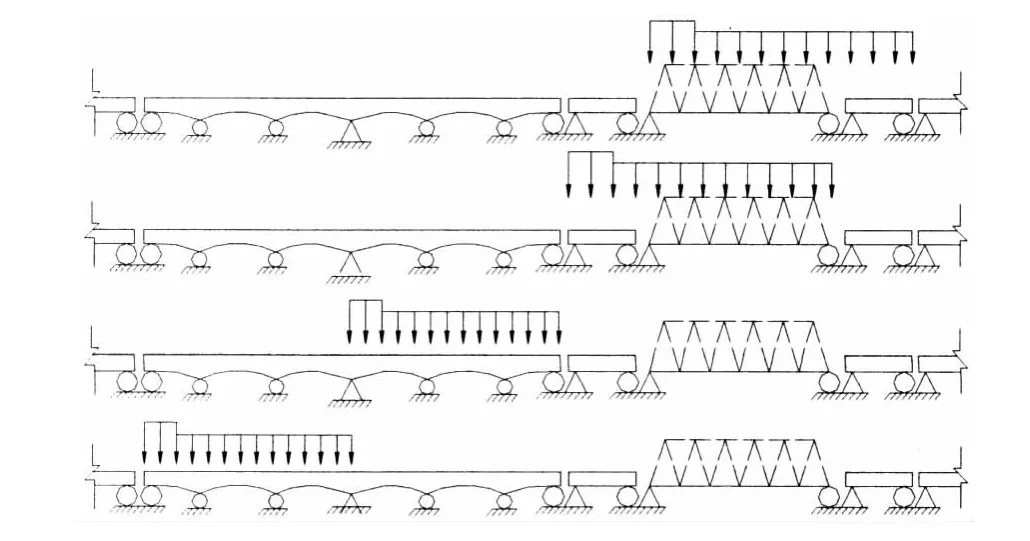
图2 列车活载加载工况示意图Fig.2 Train living load loading conditions
计算钢轨制动力时,轮轨黏着系数取0.164[12],等效均布加载于钢轨单元上,加载位置同挠曲力,分为左侧入桥和右侧入桥2种情况计算[13].
计算断轨力时,最高轨温为61℃,最低轨温为-15℃,取钢轨最大降温45℃,在钢轨受力较大的钢桁梁右端(活动支座端)、连续梁左端、连续梁右端3处折断[14].
2 钢桁梁桥上无缝线路纵向力
桥上无缝线路纵向力包括伸缩力、挠曲力、制动力和断轨力.
2.1 钢轨伸缩力
将钢桁梁整体升温25℃,混凝土梁升温15℃,计算钢轨伸缩力,如图3所示.
由计算可知,钢轨最大伸缩拉应力为47.0MPa,出现在钢桁梁桥跨中附近;压应力最大值为73.7MPa,出现在钢桁梁右侧活动支座端.钢轨伸缩拉应力区段出现突变的原因是突变处纵梁设置了断开,使得温度作用下钢轨的伸缩拉应力得到了一定程度的释放.其余梁端处由于下部结构刚度改变,应力也出现不同程度的突变.另外由于相邻连续梁温度跨度较大,在连续梁两边跨端部产生了较大应力值.
钢桁梁右侧活动支座端纵梁产生最大纵向位移36.4mm;钢轨的最大纵向位移为20.9mm,位置在靠近钢桁梁活动支座的节间内.另外纵梁和钢轨的纵向位移在连续梁边跨端均出现较大峰值.
2.2 钢轨挠曲力
取图2中4种最不利工况下钢轨挠曲力,计算结果如图4所示.
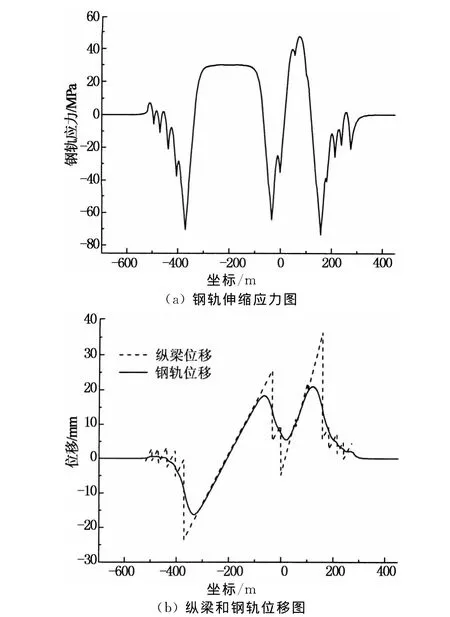
图3 钢轨伸缩力工况计算结果Fig.3 Calculation results of rail expansion stress

图4 钢轨挠曲应力包络图Fig.4 The envelope diagram of bending rail stress
由于应力得到了释放,钢轨挠曲拉应力在纵梁断开处出现了两处峰值,最大值为35.9MPa;钢桁梁活动支座端产生了最大压应力,其值为25.6 MPa,仅为最大伸缩应力值的1/3.挠曲力峰值也出现在其他梁端处.
2.3 钢轨制动力
制动力分为左侧入桥和右侧入桥(制动力大小相等、方向相反)进行计算,加载工况同挠曲力,计算结果如图5所示.
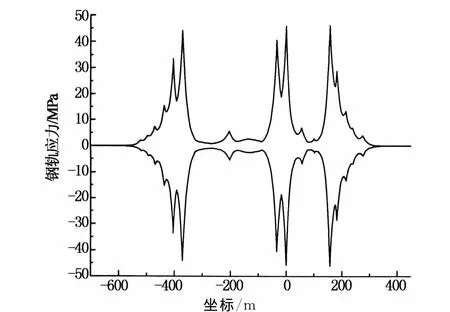
图5 钢轨制动应力包络图Fig.5 Envelope diagram of rail braking stress
由图5可以看出,钢轨制动应力包络值为上下对称分布,在钢桁梁左右两端、连续梁两边跨末端,钢轨制动应力均出现了峰值,最大值(钢桁梁右端)为46.1MPa,约为最大伸缩应力值的一半.在峰值两侧的位置处应力值降低较快.
2.4 钢轨断轨力
在钢轨降温45℃工况下,计算不同位置处折断的钢轨断轨力和钢轨位移(如图6所示).

图6 钢轨断轨工况计算结果Fig.6 Calculation results of breaking stress
在折断处钢轨应力均为0,并向两侧迅速增大.在远离折断处,钢轨应力达到最大.钢轨应力在其余梁端位置出现了不同程度的突变.
对于本桥而言,在不同位置折断时钢轨位移的变化规律基本一致,虽然钢轨在三处折断处的位移值不同,但产生的断缝宽度相差不大,断缝宽度值分别为:48.7mm(连续梁左端折断)、50.0mm(连续梁右端折断)、50.8mm(钢桁梁右端折断).
3 设计参数分析
影响大跨度钢桁梁桥梁轨相互作用的主要参数包括相邻简支梁支座布置,桥墩顶纵向刚度,小阻力扣件的布置方式.
3.1 相邻简支梁支座布置方式
为比较相邻桥跨(简支梁)约束方式对钢桁梁桥梁轨相互作用的影响,设置了如表1所示的4种支座布置形式进行分析.
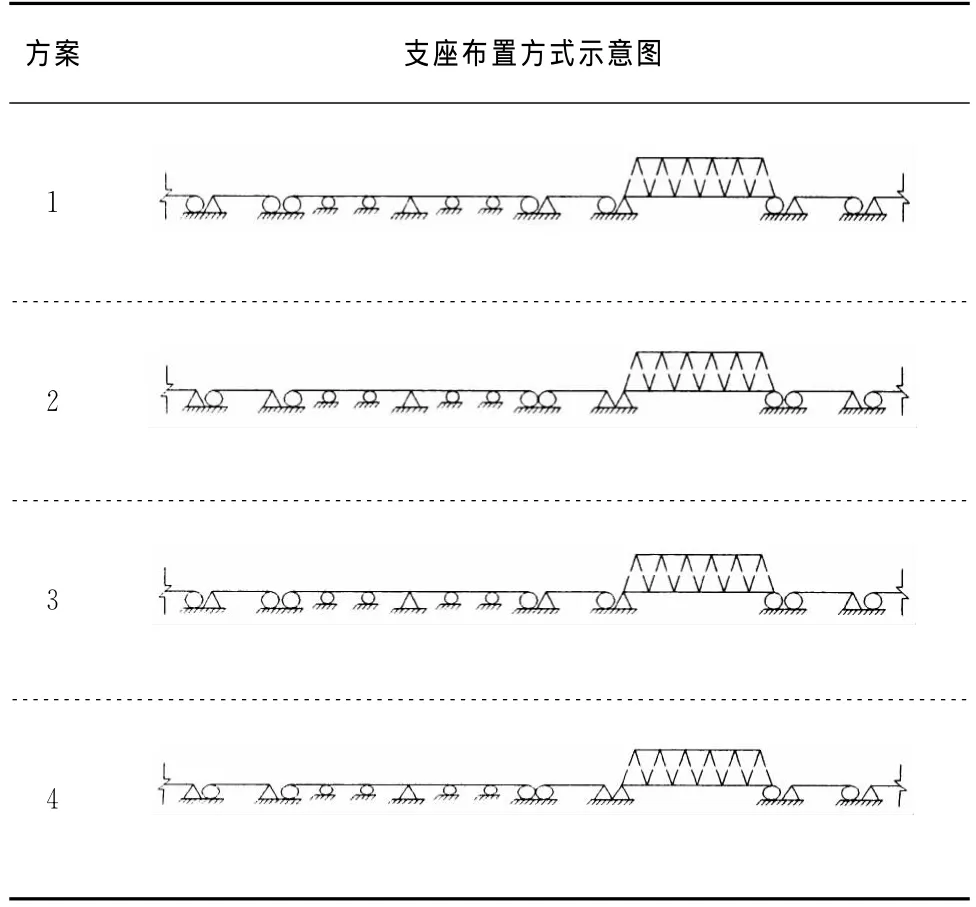
表1 相邻简支梁支座布置方案Tab.1 Bearing arrangement plans of adjacent simply supported bridges
在4种支座布置方案下,计算钢轨伸缩力与各桥墩水平力,结果见表2和图7.
对于本钢桁梁桥而言,相邻简支梁支座布置方式对钢轨伸缩力影响较小,其中方案1与方案4最大伸缩应力值相对其他方案偏小,且两者比较接近.考虑到对于所受水平力最大的12号墩(钢桁梁制动墩),方案1的桥墩水平力值较方案4减少了12%,是由于此跨简支梁固定支座布置在11号墩上,分担了水平受力.故本桥选用方案1的简支梁支座布置方式.
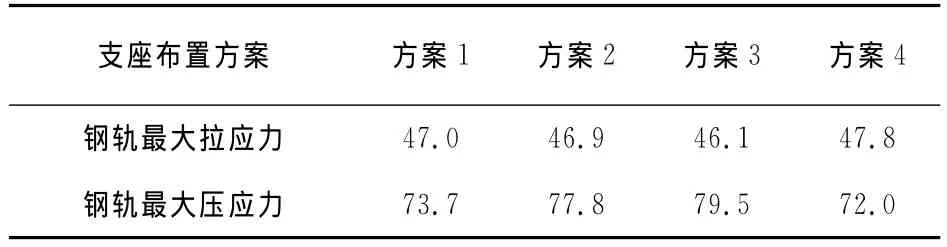
表2 不同支座布置方案下钢轨伸缩应力Tab.2 Rail expansion stress with different bearing arrangement plans MPa

图7 支座布置方案对桥墩水平力的影响Fig.7 Impact of bearing arrangement plans on pier horizontal force
3.2 桥墩顶纵向刚度
本文采用以下几种不同的桥墩顶纵向刚度值:K=500kN/cm,1 000kN/cm,2 000kN/cm,5 000kN/cm,10 000kN/cm,来探讨其对钢轨纵向力的影响规律.
通过计算钢轨伸缩力(图8)可以看出,当墩顶纵向刚度值增大时,钢桁梁左侧固定支座端到跨中的节间,以及钢桁梁右侧活动支座端(压应力最大值处)的钢轨应力增大趋势显著.钢轨纵向力最大值汇总于表3,由表3知,随着墩顶纵向刚度的增加,钢轨伸缩应力和挠曲应力的最值有增大趋势,制动应力的最值有减小趋势.

图8 墩顶纵向刚度对钢轨伸缩应力的影响Fig.8 Impact of pier longitudinal stiffness on rail expansion stress
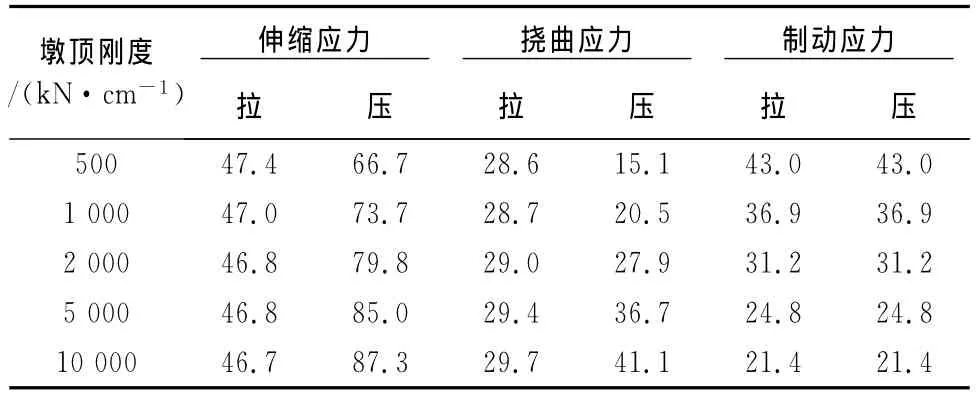
表3 钢桁梁上无缝线路纵向力最大值Tab.3 Maximum longitudinal stress of CWR in steel truss bridges MPa
3.3 小阻力扣件布置方式
小阻力扣件可以改善钢轨纵向力分布,减小应力幅值,本文考虑以下4种布置方案:
方案1:仅在钢桁梁桥上布置小阻力扣件;
方案2:在钢桁梁桥上和两端相邻1跨简支梁上布置小阻力扣件;
方案3:在钢桁梁桥上和两端相邻2跨简支梁上(以及连续梁两端的边跨上)布置小阻力扣件;
方案4:在钢桁梁桥上和两端相邻3跨简支梁上(以及连续梁两端的边跨上)布置小阻力扣件.
由钢轨伸缩力计算图(图9)看出,在钢桁梁上布置小阻力扣件后钢轨最大伸缩压应力(钢桁梁活动支座端)与拉应力(钢桁梁跨中附近)均显著减小,大大降低了应力的峰值.与一般扣件方案相比,方案1的钢轨最大伸缩拉、压应力降幅明显,分别为36.0%和33.5%.方案4相对于方案1的应力降幅仅为9.4%.由此得出,在相邻桥跨上布置小阻力扣件对钢桁梁上钢轨应力影响不大.另外由方案3和方案4看出,连续梁的应力峰值显著降低,因此在相邻连续梁边跨段应布置小阻力扣件.

图9 小阻力扣件布置方案对钢轨伸缩应力的影响Fig.9 Impact of small resistance fasteners plans on rail expansion stress
4 结 语
由于温度跨度大(钢桁梁承受的日温差也较大),本156m简支钢桁梁桥的最大伸缩应力可达73.7MPa,成为主要控制性荷载.由于其竖向刚度相对较小,其上无缝线路也承受了较大的挠曲力和制动力,分别为35.9MPa和46.1MPa,在检算钢轨强度和稳定性时应予以考虑.各钢轨纵向力均在梁端下部结构刚度发生突变处取得峰值.
相邻简支梁与钢桁梁宜采用相同方向的支座布置方式,可减小钢桁梁上钢轨伸缩力和钢桁梁制动墩所受的水平力,并使其他墩所受水平力分布更为均衡.
桥墩顶纵向刚度对钢轨纵向力有较大影响,随着墩顶纵向刚度的增加,钢桁梁上钢轨的伸缩力和挠曲力增大,制动力减小.
在钢桁梁范围内布置小阻力扣件可减小钢轨伸缩力36%.
[1] 广钟岩,高慧安.铁路无缝线路 [M].北京:中国铁道出版社,2005:2-35.
GUANG Zhong-yan,GAO Hui-an.Railway CWR [M].Beijing:China Railway Publishing House,2005:2-35.(In Chinese)
[2] SONG M K,NOH H C,CHOI C K.A new three-dimensional finite element analysis model of high-speed train-bridge interactions[J].Engineering Structures,2003,25(13):1611-1626.
[3] RUGE P,BIRK C.Longitudinal forces in continuously welded rails on bridge decks due to nonlinear track-bridge interaction[J].Computers &Structures,2007,85(7/8):458-475.
[4] READ D,LOPRESTI J.Management of rail neutral temperature and longitudinal rail forces[J].Railway Track and Structure,2005,101(8):18-19.
[5] 卜一之.高速铁路桥梁纵向力传递机理研究[D].成都:西南交通大学土木工程学院,1998:8-10.
BU Yi-zhi.Research on the transmission mechanism of longitudinal force for high-speed railway bridges [D].Chengdu:College of Civil Engineering,Southwest Jiaotong University,1998:8-10.(In Chinese)
[6] 徐庆元.高速铁路桥上无缝线路纵向附加力三维有限元静力与动力分析研究 [D].长沙:中南大学土木工程学院,2005:19-20.
XU Qing-yuan.Static and dynamic 3Dfinite element analysis of additional longitudinal forces transmission between CWR and high-speed railway bridges[D].Changsha:College of Civil Engineering,Central South University,2005:19-20.(In Chinese)
[7] 徐庆元,陈秀方.连续梁桥上无缝线路附加力研究 [J].中国铁道科学,2003,24(3):58-62.
XU Qing-yuan,CHEN Xiu-fang.Study on additional longitudinal forces transmission between continuously welded rails and continuous beam bridge [J].China Railway Science,2003,24(3):58-62.(In Chinese)
[8] YAN Bin,DAI Gong-lian.Seismic pounding and protection measures of simply-supported beams considering interaction between continuously welded rail and bridge[J].Structural Engineering International,2013,23(1):61-67.
[9] 闫斌,戴公连.高速铁路斜拉桥上无缝线路纵向力研究 [J].铁道学报,2012,34(3):83-87.
YAN Bin,DAI Gong-lian.CWR longitudinal force of cablestayed bridge on high-speed railway[J].Journal of the China Railway Society,2012,34(3):83-87.(In Chinese)
[10]朱彬.大跨度钢箱混合梁斜拉桥无缝线路设计研究[J].铁道标准设计,2012(2):4-6.
ZHU Bin.Design of continuous welded rail upon long span cable-stayed bridge with steel-concrete composite box beam [J].Railway Standard Design,2012(2):4-6.(In Chinese)
[11]DS899/59Special procedures on railway Shinkansen bridge[S].Berlin:Bridge Research Institute of Railway Bridge Authority,1991.
[12]TB 10015—2012铁路无缝线路设计规范[S].北京:中国铁道出版社,2013:8-17.
TB 10015—2012Code for design of railway continuously welded rail[S].Beijing:China Railway Publishing House,2013:8-17.(In Chinese)
[13]赵卫华,王平,曹阳.大跨度钢桁梁桥上无缝线路制动力的计算[J].西南交通大学学报,2012,47(3):361-366.
ZHAO Wei-hua,WANG Ping,CAO Yang.Calculation of braking force of continuous welded rail on large-span steel truss cable-stayed bridge [J].Journal of Southwest Jiaotong University,2012,47(3):361-366.(In Chinese)
[14]戴公连,闫斌.高速铁路斜拉桥与无缝线路相互作用研究[J].土木工程学报,2013,46(8):90-97.
DAI Gong-lian,YAN Bin.Interaction between cable-stayed bridge traveled by high-speed trains and continuously welded rail[J].China Civil Engineering Journal,2013,46(8):90-97.(In Chinese)
Track-bridge Interaction of Long-span Simply Supported Steel Truss Bridge in Mixed Passenger and Freight Railway
YU Xiang-dong†,SHA Song,YAN Bin
(College of Civil Engineering,Central South Univ,Changsha,Hunan 410075,China)
A beam-rail-pier 3Dfinite element model was built by adopting the mechanism of ideal elastic-plastic ballast resistance under the background of a 156mlong-span simply supported steel truss bridge on Huangling-Hancheng-Houma Railway line.The purpose was to study the distribution of longitudinal force due to temperature variations,bridge deflection,braking force and the breaking force of long rail in steel truss bridges.The influences of design parameters on longitudinal forces,such as the bearing arrangements of adjacent simply supported bridges,pier longitudinal stiffness and the arrangement of small resistance fasteners,were also discussed.It has been shown that the longitudinal force due to temperature variations plays a major role.Secondly,the bearing of adjacent simply supported bridge should be in the same direction as the steel truss bridge.Thirdly,the longitudinal force due to temperature variations and structural deflection increases and the braking force decreases as the pier longitudinal stiffness increases.Finally,the small resistance fasteners have a good effect on the longitudinal force due to temperature variations,which can reduce the force by 36%after being installed.
railroad engineering;railroad bridges;steel truss bridges;track-bridge interaction;longitudinal force of rail;design parameters
U213.912
A
1674-2974(2014)06-0106-06
2013-08-28
国家自然科学基金资助项目(51378503);高速铁路基础研究联合基金资助项目(U1334203)
于向东(1970-),男,河南遂平人,中南大学副教授
†通讯联系人,E-mail:xyd77@139.com

