宽带卫星通信系统中强干扰抵消方法*
杨恒,党军宏,潘亚汉
(1.解放军理工大学 通信工程学院,南京 210007;2.总参第六十三研究所,南京 210007)
1 引言
有效载荷具有更强的星上信号处理能力是卫星通信的重要发展方向,星上处理转发器要在星上对信号进行数字域处理离不开模数转换器(Analog to Digital Converter,ADC),但当干扰增大到一定强度时,信号与干扰的合成信号瞬时幅度将会超出ADC的量程,使ADC发生削幅效应(clipping effect),即任何超出量程的输入都将被限定为ADC最大(或最小)量化电平,造成信号的严重失真[1]。为解决以上问题,星上一般采用自动增益控制(Automatic Gain Control,AGC)技术对输入信号的大小进行自动控制调整,使得到达A/D的输入信号基本保持恒定,或者使得到达A/D的输入信号在所要求的动态范围之内[2]。但当干扰足够大时,AGC环节为保证输出信号强度在ADC量程内,会对有用小信号剧烈压缩,当小信号的被压缩程度达到某一限度时,受量化噪声影响,被压缩的有用小信号AD后信噪比将大大降低,因此误码率也将急剧增大[3-4]。采用高精度ADC能减小量化噪声,但实际中受功耗、设计复杂度等影响,高精度的 ADC很难实现[5-6]。星上动态带阻陷波技术通过一系列带阻滤波器避免了干扰信号进入转换器造成溢出效应[7],目前动态滤波技术主要有两种实现方式:一种为采用滑动带阻滤波器,当检测到干扰的具体位置以及个数等信息后,实时设计或者查表给出与之对应的带阻滤波器设计参数,从而实现存在干扰位置的陷波处理;另一种为变换频域陷波,进行DFT变换后,在频域中进行相应的干扰检测和带陷滤波,最后再进行IDFT变换。但目前的动态带阻滤波技术均在模拟域进行处理,灵活性、可靠性都不高。
本文提出了自适应强干扰信号抵消技术,具体就是采用基于数字域强干扰分离、模拟域强干扰抵消思路,对强干扰信号进行抑制,减弱到达AGC环节的强干扰信号强度,避免AGC环节对有用小信号的严重压缩,进而提高有效载荷的整体瞬时动态范围。
2 总体方案
强干扰信号抵消系统由强干扰信号检测、强干扰信号提取、信号幅度相位调整、强干扰信号抵消、检测反馈回路等部分组成,系统框图如图1所示。
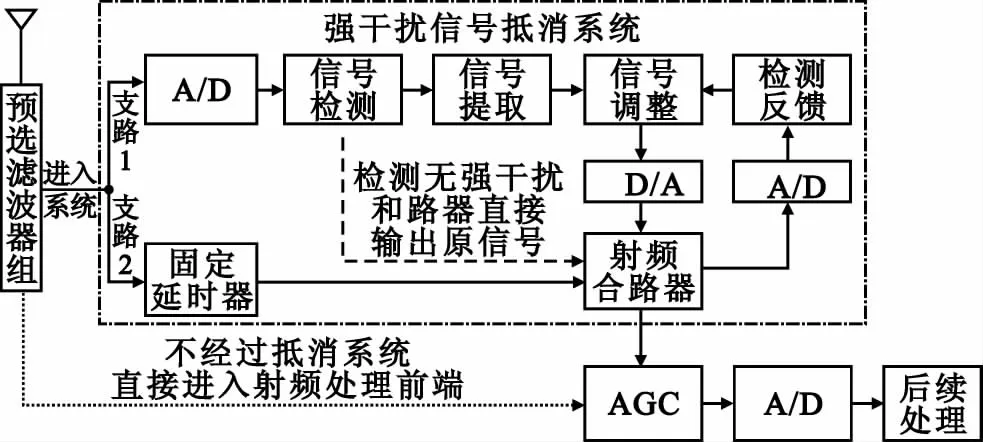
图1 抵消系统框图Fig.1 Block diagram of the proposed strong interference cancellation system
接收天线接收到的信号经预选滤波器组进行目标频段提取,采用功分器把接收射频信号一分为二,分成信号固定延时支路和强干扰信号检测、分离、参数调整支路(本文为了便于叙述,以下把信号固定延时支路称为支路1,把强干扰信号检测、分离、参数调整支路称为支路2)。把支路1的输出信号和支路2的输出信号通过合路器相加,以达到抵消强干扰信号的目的。为确保抵消效果,检测反馈模块将对强干扰信号的剩余信号强度进行检测,如满足要求,则保持信号幅度、相位参数;如剩余干扰强度依然太大,则继续调整参数至输出符合要求。为了实现更好的抵消效果,还可采用多个强干扰抵消系统串行级连的方式进行处理。
3 具体实现方法
3.1 强干扰信号检测
强干扰信号检测模块是整个强干扰信号抵消单元的基础,需要对接收信号进行处理,做出是否存在强干扰信号的判决,其框图如图2所示。

图2 强干扰信号检测框图Fig.2 Block diagram of strong interference detection module
同时,为进一步提高系统性能,如果能准确确定出有用弱信号的具体参数特性(中心频率、信号带宽等),在后续处理中,我们可以利用自适应波束形成的方法有效提高信噪比。自适应波束形成是数字波束形成中的一个子类,其核心是采用自适应算法,利用数字信号处理技术提高系统性能及通信容量等,因此,准确获得宽频带内有用信号的具体参数具有重要作用。有关数字波束成形的内容可参考文献[8]。
在依据判决门限进行判决并确定强干扰信号的占用频带(图3中An至Bn),同时确定宽频带内各有用信号,尤其微弱有用信号的具体参数时,由于卫星通信宽频带范围内噪声基底的不同会对信号的判决造成偏差,尤其可能对噪底较高的有用小信号造成误判,因此需要在进行判决前消除噪底起伏的影响。
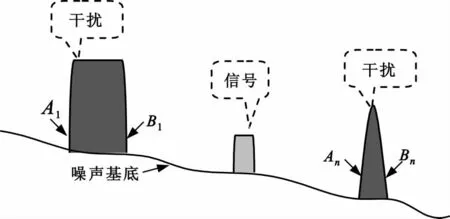
图3 频谱分布图Fig.3 Spectrum distribution
常用的噪声基底估计方法是在切断输入信号的情况下测量接收机的噪声基底。然而,接收机前端噪声基底的频谱特性会随着器件老化、外部温度和湿度、信号环境、器件工作参数等因素的变化而变化,并且测量工作繁琐反复。为此,本文采用数学形态学滤波方法首先估计出噪声基底,排除噪底干扰后再根据修正频谱的统计特征估计出自适应动态检测门限。
形态学的基本思想是用具有一定形态结构的结构元素去探测一个图像中的形态,主要解决图像的理解分析问题。结构元素在数学形态变换中的作用类似信号处理中的滤波器。设信号f为定义在F={0,1,2,…,N-1}上的离散函数,结构元素 g 为 G={0,1,2,…,M-1}上的离散函数,且有 N>M,则4 种基本形态变换定义为
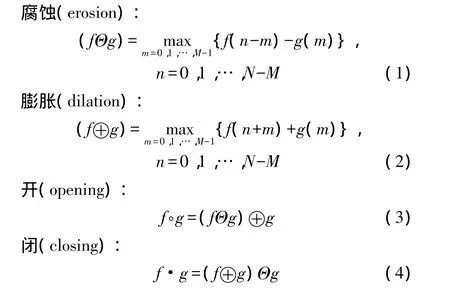
在数据分析中,腐蚀运算扩展信号谷域,减小信号峰值,膨胀运算减小信号谷值,扩展信号峰顶。先腐蚀后膨胀的过程称为开运算,能平滑图像轮廓,消除尖峰、凸缘。先膨胀后腐蚀的过程称为闭运算,闭运算也能使图像轮廓平滑,同时抑制信号波谷[9]。当取线性结构元素时,膨胀运算可等价于最大值滤波,腐蚀运算可等价于最小值滤波,开运算可通过最小值滤波和最大值滤波级联实现。图4给出了用数学形态学分析估测噪声基底的原理图。
首先将所得谱线以m(图中取3)为单元分段,分段后有3种情况,即分段内所有谱线都为基底噪声的谱线、部分谱线为基底噪声和所有谱线都为信号的谱线,如图4(a)所示。将每个单元中最小值取出后得到新的谱线,对最小值作开运算,将进行开运算后的值与开运算前的值作差,差的绝对值很小的谱线可视为各个单元噪声基底的估计值,对各单元噪底估计值进行内插运算得到噪声基底谱线,如图4(b)所示。原有谱线减去噪底谱线近似为在高斯白噪声上叠加了信号谱线和干扰谱线,这样就消除了卫星通信宽频带范围内噪底起伏的问题,如图4(c)所示。
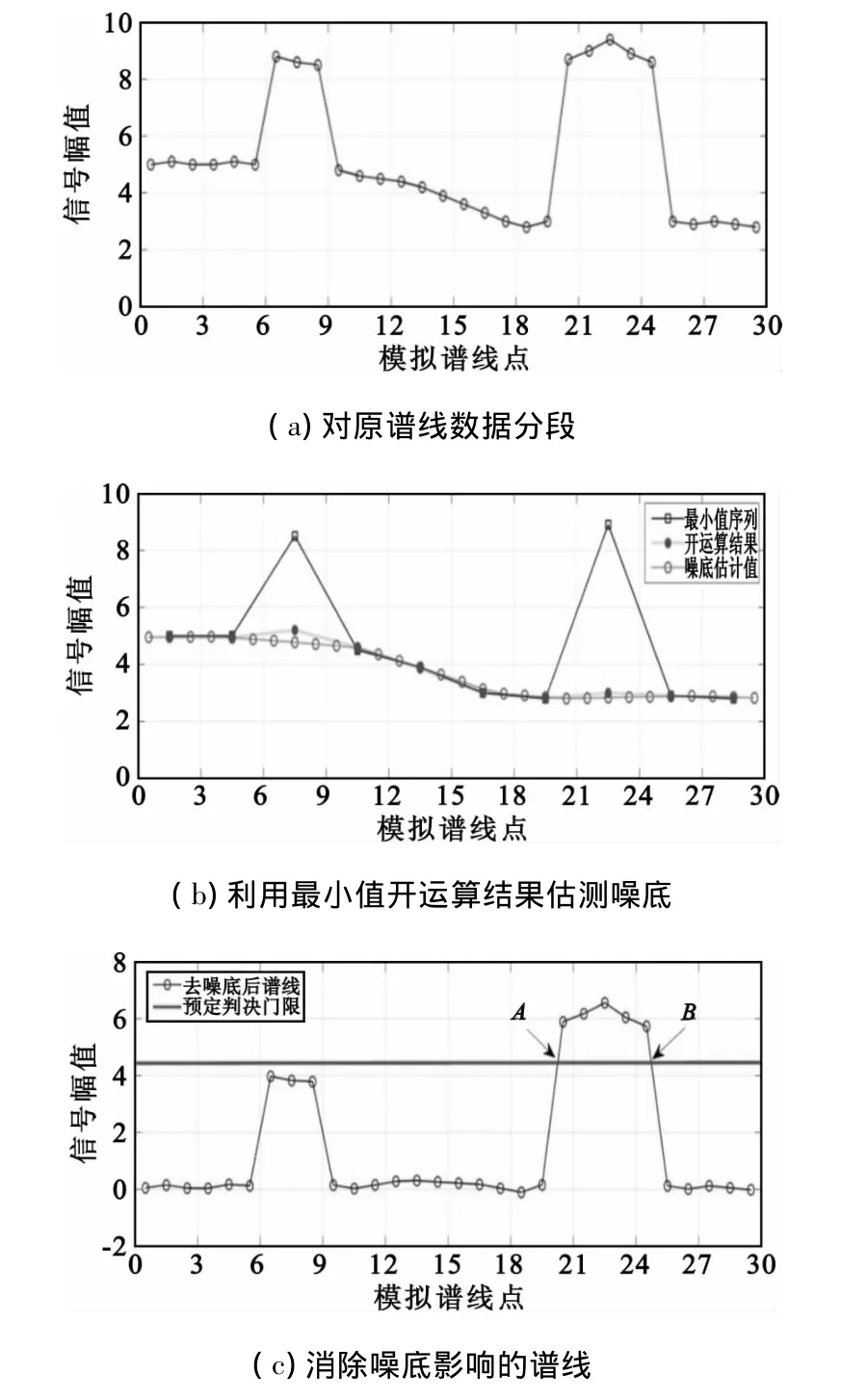
图4 消除噪底原理的图形描绘Fig.4 Principle description for noise floor elimination
此时则可直接根据信号强度的大小判定小信号的具体位置以及是否存在强干扰信号。对于小信号具体位置,可以采用N-Sigma方法对未叠加信号的谱线进行处理来估计检测门限:
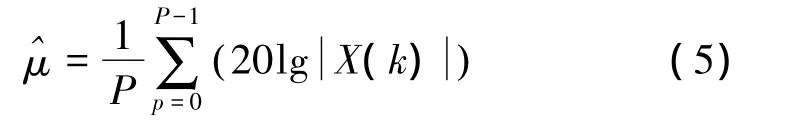
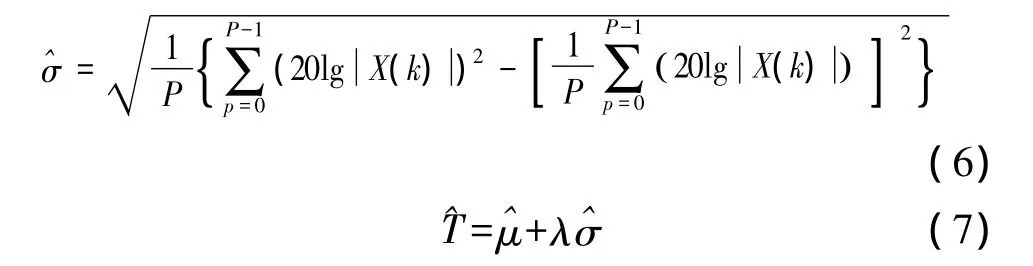
3.2 强干扰信号提取
本文采用数字FIR带通滤波器对强干扰信号进行提取,其核心问题是根据已知强干扰信号的占用频带快速设计出适用的FIR带通滤波器。为尽可能降低提取强干扰信号的复杂度,并能快速设计出FIR带通滤波器,本文提出以预先设计好的两组FIR带通滤波器为基础,构造各种适用的FIR带通滤波器,如图5所示。

图5 预先设计基本FIR带通滤波器中部分FIR带通滤波器的幅频响应Fig.5 Amplitude-frequency response of compound filters
图5中设计的基本滤波器过渡带带宽、通带带宽均相同,每个基本滤波器的通带波动为0.01dB,阻带衰减为90dB。每个基本滤波器均可独立使用,当强干扰处于FIR带通滤波器1的通带范围内,则仅使用滤波器1即可。当强干扰信号的占用频带超出滤波器1的范围,则相邻的基本滤波器可组合使用,以形成通带范围更宽的带通滤波器。如图5中基本FIR滤波器1与基本FIR滤波器2可构成复合滤波器1,基本FIR滤波器3与基本FIR滤波器4可构成复合滤波器2,其幅频响应如图6所示。
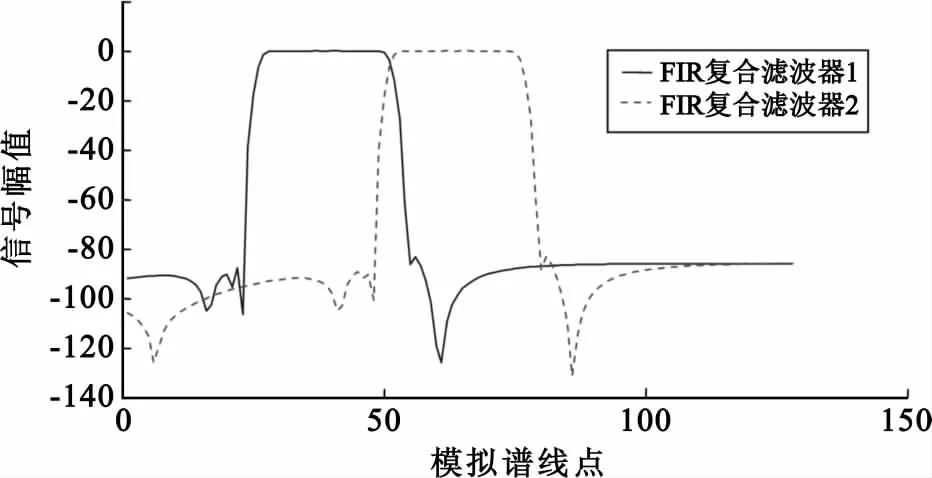
图6 复合滤波器的幅频响应Fig.6 Amplitude-frequency response of composite filters
图6中所示每个复合FIR滤波器各自的通带波动为0.1dB,阻带衰减为90dB。当强干扰信号处于复合滤波器1的通带范围内时,则可以采用复合滤波器1把强干扰信号提取出。通过以上设计方式,我们可以利用两组基本的FIR带通滤波器快速构造出各类适用的复合滤波器对强干扰信号进行提取。
3.3 强干扰幅度相位调整与抵消
提取出的强干扰信号在射频合路器与原信号进行抵消时,若幅度或相位不合适,则可能造成抵消失效甚至增大干扰,因此需要对提取的强干扰信号进行幅度和相位调整。
幅度调整由两部分构成,大步进信号幅度调整由增益可控放大器实现,小步进信号幅度调整采用数字方法实现。相位调整通过延时实现,延时分为整数采样周期延时调整和小数采样周期延时调整,其中整数采样周期延时调整通过移位寄存器实现,小数采样周期延时调整可通过多相内插滤波器实现,如图7所示。
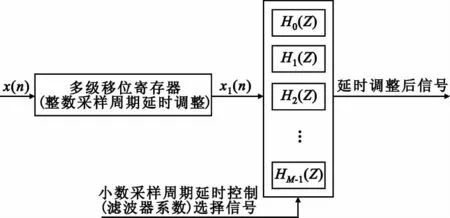
图7 采样周期延时调整Fig.7 System model of sampling period delay adjustor
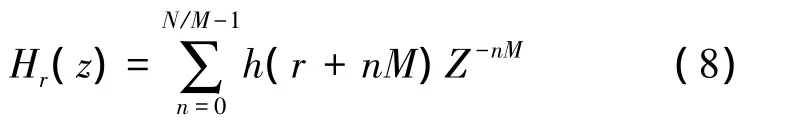
对通带截止频率为 f1、通带波动0.1dB,阻带起始频率为f2、阻带衰减90dB,滤波器阶数为N的FIR低通滤波器进行M相分解,即形成M个16阶单通道滤波器,x1(n)通过滤波器H1(z)得到的结果比x1(n)通过滤波器H0(z)得到的结果超前1/M采样周期,依次类推。所以通过选择不同的单通道滤波器Hr(z)就可以实现不同的小数采样周期延时。
调整后的强干扰信号与经过固定延迟器的原始信号在射频合路器相加即可实现强干扰抵消。有关射频合路器的特性参考文献[10]。
3.4 检测反馈
理论上如果提取出的强干扰信号与原始信号中的强干扰信号幅度相同,相位相差180°,则该强干扰信号可以完全抵消。但在实际实现中由于提取并调整后的强干扰信号无论在幅度还是相位上都与原始强干扰信号可能存在偏差,所以需要一个检测反馈环节来检测强干扰信号的抵消效果,主要是将抵消后的剩余干扰信号幅度与原干扰信号幅度进行对比,当抵消后的效果达不到预设定值(一般可设为40dB)时,调整模块先固定提取强干扰信号的幅度,采用整数采样周期延时调整和小数采样周期延时调整让提取强干扰信号的相位调整到最佳,再固定信号的延时参数,对信号幅度进行调整。通过调整使抵消后的剩余干扰信号幅度满足预设定值的要求后,保持信号幅度、相位参数,再将抵消后的射频信号送入后续处理。
4 仿真结果分析
图8为Eb/n0取10dB、谱线分段m取5、滤波器通带波动0.01dB、阻带衰减90dB、单音干扰条件下相位调整从0~2π的抵消效果图。图中抵消效果最好为63 dB,最差时为-6 dB,即调整后与原干扰信号正好相位相差180°,幅值扩大1倍,造成性能恶化。
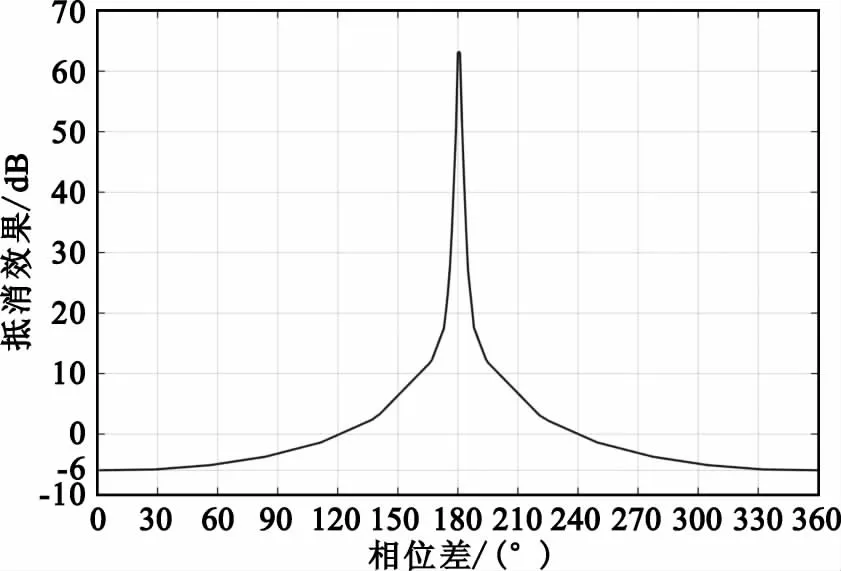
图8 不同相位抵消效果对比图Fig.8 Cancellation result comparison for various phases
图9为Eb/n0取10dB、谱线分段m取5、滤波器通带波动0.01dB、阻带衰减90dB、窄带干扰条件下抵消前后的对比图。从图中可以看出,抵消系统能对窄带干扰进行62 dB的抑制。
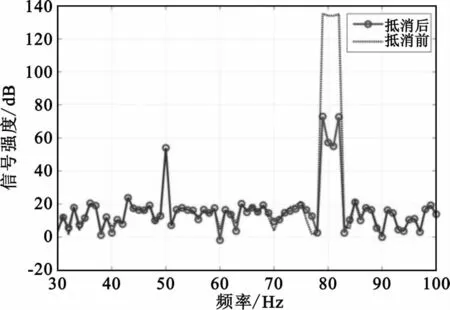
图9 抵消系统对窄带强干扰抑制效果图Fig.9 Narrow band strong interference suppression result
在工程实现中,由于数字域提取、模拟域抵消强干扰需要分别使用ADC和DAC,ADC转换后的数字信号与原模拟信号相比,叠加了高斯白噪声,DA转换后的模拟信号与原数字信号相比,也将叠加高斯白噪声,这将会对抵消效果造成一定的影响。图10为与图9相同仿真条件下,假设原模拟信号与AD转换叠加的高斯白噪声相比,SNR取80dB,DAC的SNR分别取60dB、70dB及理想情况的窄带干扰条件下抵消后的对比图。仿真结果表明,当DAC的SNR取70dB时,抵消效果与不考虑DAC造成影响的理想情况相近,而目前高速DAC的SNR超过70dB,满足工程要求。
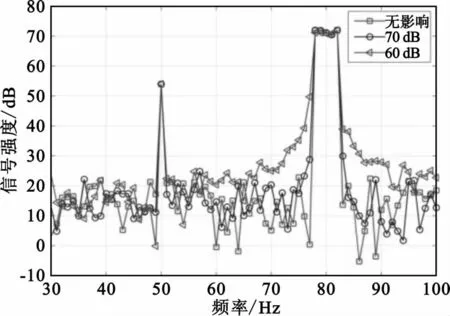
图10 DAC取不同SNR抵消效果对比图Fig.10 Cancellation result comparison for different SNR of DAC
图11为与图9相同仿真条件下,将频率为50Hz的单音信号视为有用信号,对中心频率为80Hz、强度超过有用信号50~95 dB的强干扰信号进行抵消,抵消后有用信号信噪比与不进入抵消系统的有用信号信噪比对比图。仿真中,计算信噪比时对有用信号进行10Hz滤波,ADC的SNR设为80dB。仿真结果表明,当强干扰信号逐渐增大至55 dB以上时,有用信号信噪比迅速降低。而经过抵消系统后,有用信号信噪比基本保持恒定。
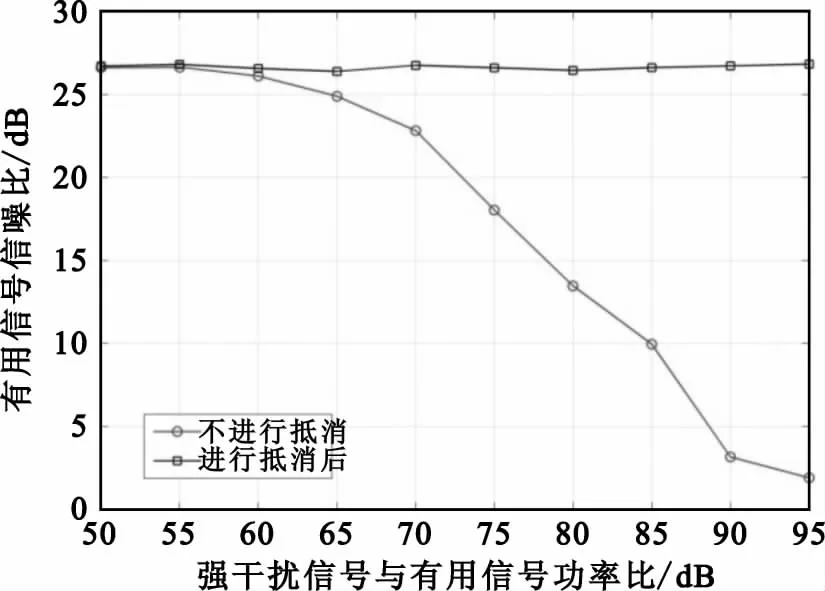
图11 有用信号信噪比对比图Fig.11 Comparison for various desired signal SNR
5 结束语
本文针对星上处理转发器受强干扰信号影响时,AGC环节为保证合成信号不超过ADC量程严重压缩有用小信号的问题,提出了强干扰信号抵消技术,对强干扰信号进行数字域提取、模拟域抵消,并利用数学形态学滤波消除了卫星通信宽频带范围内噪声基底不平带来的影响,为后续处理时进行小信号波束成形提供了所需参数,提出了工程适用的提取强干扰信号的滤波器设计方法,仿真验证了抵消系统能对强干扰信号进行有效抑制,避免了AGC环节对有用小信号严重压缩导致的信噪比降低。
[1]Walden R.Analog-to-digital converter survey and analysis[J].IEEE Journal on Selected Areas in Communications,1999,17(4):539-550.
[2]Dardari D.Joint clip and quantization effects characterization in OFDM receivers[J].IEEE Transactions on Circuits and System,2006,53(8):1741-1748.
[3]Hua Y,Liang P,Ma Y,et al.A method for broadband full-duplex MIMO radio[J].IEEE Signal Processing Letters,2012,19(12):793-796.
[4]Kumar R,Taggart D,Chen C.Probability of Error Analysis of Analog-to-Digital Converters with Multiple 8-PSK Modulated Signals[C]//Proceedings of the 2005 IEEE Aerospace Conference.Big Sky,MT:IEEE,2005:1705-1712.
[5]Dabeer O,Madhow U.Channel Estimation with Low-Precision Analog-to-Digital Conversion[C]//Proceedings of 2010IEEE International Conference on Communications.Toronto,Canada:IEEE,2010:1-6.
[6]Singh J,Madhow U.On block noncoherent communication with low-precision phase quantization at the receiver[C]//Proceedings of 2009 International Symposium on Information Theory.South Korea:IEEE,2009:2199-2203.
[7]张邦宁,魏安全,郭道省.通信抗干扰技术[M].北京:机械工业出版社,2006.03.ZHANG Bang-ning,WEI An-quan,GUO Dao-xing.Anti-jamming Technology in Communications[M].Beijing:Machineary Industry Press,2006.(in Chinese)
[8]何业军,桂良启,李霞.智能天线[M].北京:电子工业出版社,2009.HE Ye-jun,GUI Liang-qi,LI Xia.Smart Antenna[M].Beijing:Publishing House of Electronics Industry,2009.(in Chinese)
[9]Ao C,Yang X,Zhang C.A Sort of Improved Image Segmentation Algorithm Based on Geometry Characteristc[C]//Proceedings of 2010IEEE WCICA.Taipei,Taiwan:IEEE,2010:58-62.
[10]Pozar D M.Microwave Engineering[M].3rd ed.Hoboken,NJ:Wiley,2005.

