变权重蛙跳算法在PMU 优化配置中的应用

牛胜锁，张思为，梁志瑞

（华北电力大学新能源电力系统国家重点实验室，保定071003）

相量测量单元PMU（phasor measurement unit）是基于全球定位系统GPS 的一种相量测量装置，PMU 能够实现广域电网运行状态的实时同步测量，为实现电力系统全局稳定性控制创造了条件，克服了现有以监控与数据采集系统、能量管理系统为代表的调度检测系统不能检测和辨识电力系统动态行为的缺点[1]。

在保证系统完全可观测情况下，如何在电网中合理配置较少数目的PMU 是目前一个较为热点的研究课题。针对此类问题通常考虑两个方面：PMU 最优数目的确定和PMU 安装位置的确定。文献[2]提出了一种概率偏移粒子群算法，该方法对小规模网络求解效率高，但不善于求解复杂网络。文献[3]提出一种遗传算法和模拟退火法组合算法，有较强爬山性能，但收敛方向不准确，影响迭代效果；文献[4]提出一种改进禁忌搜索法，避免了重复搜索，但缺乏搜索方向指引，较难得到最优结果。

本文提出一种变权重蛙跳算法[5]VWFLA（weighted and shuffled frog leaping algorithm）解决PMU 优化配置问题。该方法以PMU 配置数目最小为目标函数，以电力系统可观测为约束条件，设计了算法的适应度函数，结合混合蛙跳算法的蛙体跳跃进化方式，并改进权重系数的更新策略，进一步提高了收敛效果和最优解集多样性。最后通过对各方案进行冗余度分析得出最优方案。

1 PMU 优化配置问题的数学模型

1.1 PMU 测量规则

电力系统的节点电压和支路电流可以通过直接测量或虚拟测量的方式获得。其中虚拟测量是利用与其相关的测量经计算而得出待测量的方法。在电网中，结合欧姆定律和基尔霍夫电压电流定律，得出以下4 条测量规则[6]：

（1）配置PMU 的节点，其节点电压和与该节点相关的支路电流可直接量测，与该节点相邻节点的电压相量可计算得到；

（2）已知支路两端节点电压相量，则该支路电流可计算得到；

（3）未配置PMU 的零注入节点若其电压已知，且其相关支路只有一条不可观测，则该支路电流可计算得到；

（4）若零注入节点所有相连的节点电压都已知，则该节点电压可计算得出。

1.2 电力系统可观的定义

如果PMU 量测能提供足够的测量信息，从而通过状态估计可计算出系统全部状态量，就称系统是可观的。系统可观性可从代数可观与拓扑可观两种角度考察[6-8]。代数可观计算需要满秩的电网信息矩阵，计算量大、速度慢。本文结合系统拓扑信息和注入信息求解可观测性问题，计算量和计算速度均优于代数可观。而拓扑可观是将电力系统看作一个由n 个顶点、b 条边构成的图，即

式中：V 为图的顶点集合；E 为图的边集合。分别对应于系统的母线和支路集合。基于测量规则的测量网络构成一个测量子图，即

式中：V′⊆V；E′⊆E。如果测量子图G′与图G 的关系满足V⊆V′，即子图G′包含图G 的所有顶点，则系统拓扑可观。

1.3 问题的数学模型

由以上PMU 测量规则和电力系统可观测判断方法，PMU 优化配置问题的数学模型可表述为

式中：X 为n 个节点的PMU 配置矩阵，X=[x1，x2，…，xn]T，若第i 个节点配置PMU，则xi=1；否则xi=0；A 为支路-节点关联矩阵。目标函数为配置PMU的数目最小，约束条件为系统完全可观测（判据为：向量XA 中值最小的元素大于零，即每个元素均大于零）。

2 混合蛙跳算法的基本原理

混合蛙跳算法HFLA 是由Eusuff 等于2003年提出的一种新的元启发式的搜索算法，通过模拟青蛙群体在觅食过程中所体现出的协同行为来完成对问题的求解。这种算法按照族群分类进行信息传递，并将全局信息的交换与局部进化搜索相结合[9-11]。

HFLA 算法首先随机生成p 只青蛙组成初始群体，每只青蛙表示问题的解为

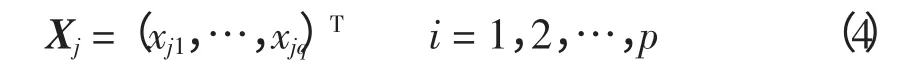
式中：j 为第j 只青蛙；q 为解空间的维数。在生成初始群体之后，将种群内青蛙个体按其适应度降序排列。然后将整个青蛙群体分成m 个子群，每个子群包含n 只青蛙。其中，第1 只青蛙分入第1 子群，第2 只青蛙分入第2 子群，第m 只青蛙分入第m 子群，第m+1 只青蛙分入第1 子群，第m+2只青蛙分入第2 子群，依次类推，直到全部青蛙划分完毕。

子群中青蛙个体进化时，首先借助子群最好个体Xpb与最差个体Xpw产生新个体Xpw，new（视为青蛙的一次跳跃）。更新策略为

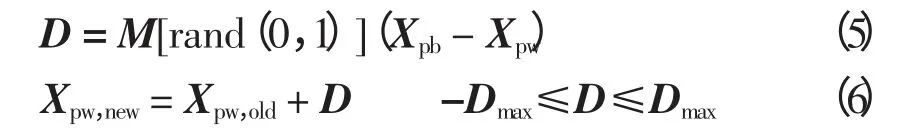
式中：D 为各分量的移动距离矩阵；M（rand（0，1））为0 和1 之间的随机数矩阵；Dmax为青蛙所允许改变位置的最大值。

如果Xpw，new的适应度优于其父代个体Xpw，则替换之；否则借助种群最优个体Xgb与该子群的Xpw重新产生新个体Xpw，new（视为青蛙的第2 次跳跃）。如果优于父代个体则替换之；否则随机产生一个新个体Xpw，new（视为青蛙的第3 次跳跃）替换父代个体。重复3 次跳跃式的更新操作直到设定的迭代次数。当所有子群局部深度搜索完成后，将所有子群的青蛙重新混合并排序和划分子群，然后再次进行局部深度搜索，重复此操作直到满足终止条件[11-12]。

3 变权重蛙跳算法求解PMU 优化配置问题

3.1 蛙体的结构编码

在蛙跳算法中，相关参数大部分属于连续实数域，因此蛙跳算法主要适用于连续空间域的优化问题，难于直接处理离散的组合优化问题[13]。PMU 优化配置问题属于离散组合优化问题，所以在分析传统蛙跳算法优化机理的基础上，本文采用了整数编码方式。第j 只青蛙的位置可表示为

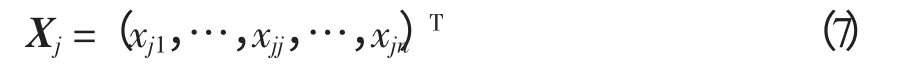
式中的各维变量分别表示PMU 在n 个节点电力系统中的配置情况，xjk=0 表示不在k 节点配置PMU，xjk=1 表示在k 节点配置PMU。

3.2 蛙体的变权重更新策略

在电力系统线性量测模型的基础上，根据蛙体跳跃进化的特点，构建系统状态可观性评估的适应度函数为

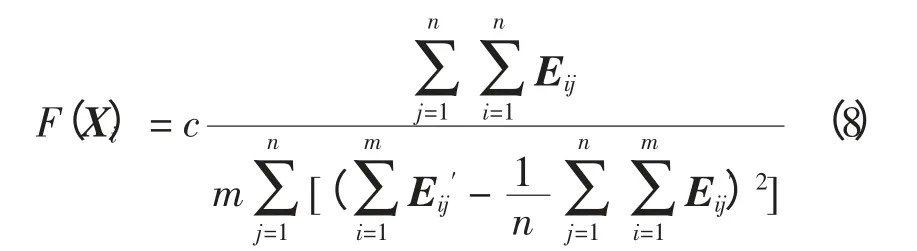
式中：E 为n×n 网络拓扑矩阵；E′为Xi对应的m×n可观测网络矩阵；c 为惩罚因子，若系统完全可观测，则c=1；否则c 取一个较小数值。对不能达到完全可观测的蛙体Xi降低其适应度。

通过种群内青蛙个体的适应度进行降序排列，并分成若干子群，子群中青蛙个体进化的第1次跳跃变化为

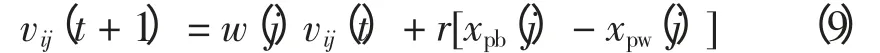
式中：vij（t）为蛙体i 在第t 次迭代时移动速度矩阵的第j 维分量；w 为权重系数；r 为介于[0，1]之间的随机数。新个体为

对Xpw，new、Xpw、Xgb的适应度进行比较分析，依次进行青蛙的第2 次跳跃和第3 次跳跃，直到设定的迭代次数。

当所有蛙体完成3 次跳跃搜索后对蛙体跳跃方向进行更新。根据种群整体进化后的基因编码赋予相应的权重，对多次出现需要配置PMU 的节点赋予高权重，有利于其在跳跃的进化中继续保留，对较少出现需要配置PMU 的节点赋予低权重，提高其跳跃进化中发生变异的概率。权重系数的变化公式为

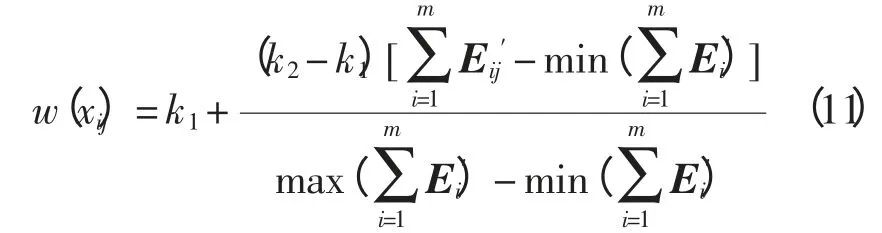
式中，k1和k2为权重系数的取值限制，可以将w（xij）钳位在[k1，k2]之间。经仿真结果分析，k1取（0.2～0.4），k2取（0.6～0.8），收敛效果较好。

3.3 冗余度分析

系统中独立测量量的数目和状态量数目之比称为冗余度。PMU 数目相等的前提下，可以通过比较不同配置方案的冗余度来确定最优方案。从而提高实时信息的可靠性与完整性[14]。

对一个n 节点系统，其状态量为n 维电压向量，其独立测量量为配置了PMU 的节点电压向量以及与之关联的电流向量。冗余度可表示为

式中：P 为配置了PMU 的节点集合；di为与配置了PMU 的节点i 相关联的支路数。

3.4 算法实现流程

变权重蛙跳算法流程如图1 所示。

4 算例分析

在Matlab 软件环境下开发了基于变权重蛙跳算法的PMU 优化配置程序，并针对新英格兰39母线系统和IEEE 57 母线系统进行了仿真分析。取蛙体个数为100 个，迭代次数为100 次。

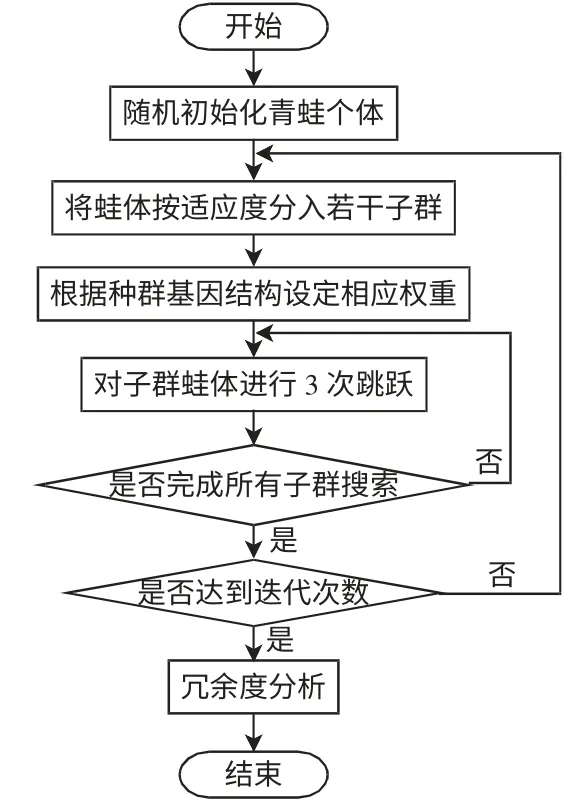
图1 变权重蛙跳算法流程Fig.1 Flow chart of VWFLA algorithm

4.1 算例1

New England 39 母线系统结构简化图见图2。

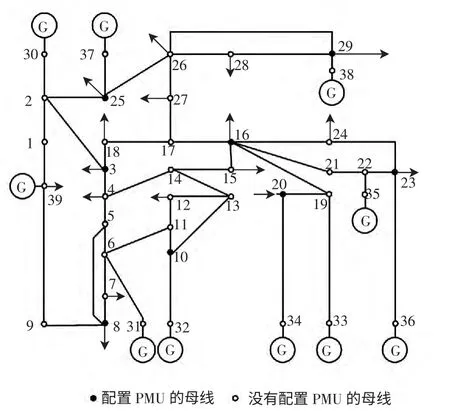
图2 New England 39 母线系统简化图Fig.2 Simplified diagram of New England 39-bus system

对图2 网络的PMU 优化配置问题分别用性能较好的遗传算法[15-17]、粒子群算法[2，18]和本文算法进行求解，几种算法的求解结果比较如表1 所示。

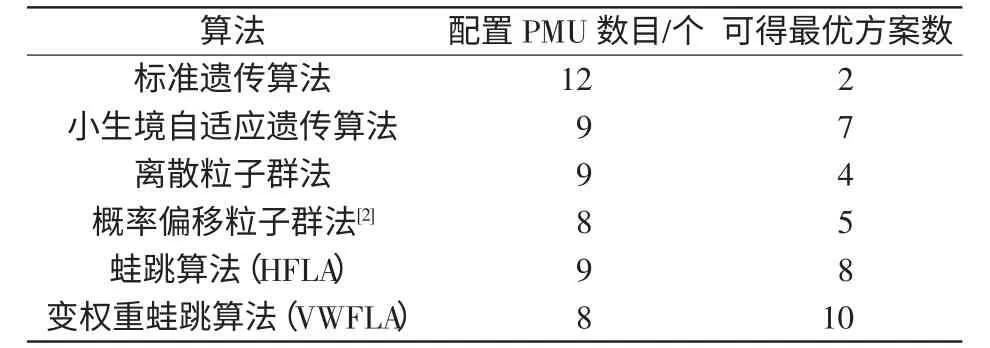
表1 几种算法比较（算例1）Tab.1 Comparison of several algorithms（case 1）

由表1 可知，在相同迭代次数下，综合考虑最优方案需配置的PMU 数目和所得最优方案个数，变权重蛙跳算法更优于其他算法。概率偏移粒子群法、蛙跳算法和变权重蛙跳算法的是其中计算效果较优的3 种算法。图3 为这3 种算法在New England 39 母线系统完全可观条件下的收敛效果分析。由图3 可以看出，变权重蛙跳算法较性能优良的概率偏移粒子群法有着更好的收敛速度，这对求解多节点复杂网络的PMU 优化配置问题更加有利。

由表1 和图3 可以看出，变权重蛙跳算法相比其它算法在搜索方向性、收敛速度、可行解数目等方面都表现得更为出色。通过该算法求得的各方案如表2 所示，优选冗余度较大的1、3 号方案。

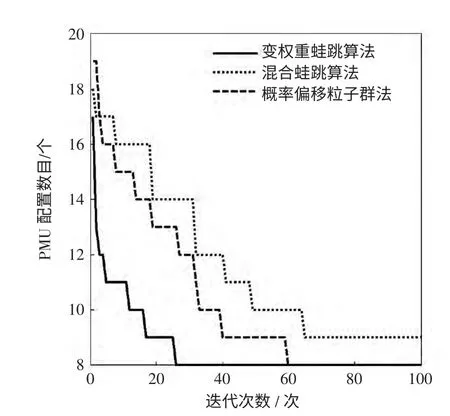
图3 New England 39 母线系统变权重蛙跳算法、混合蛙跳算法和概率偏移粒子群法的收敛效果对比Fig.3 Comparison of VWFLA，HFLA and PBPSO for New England 39-bus system

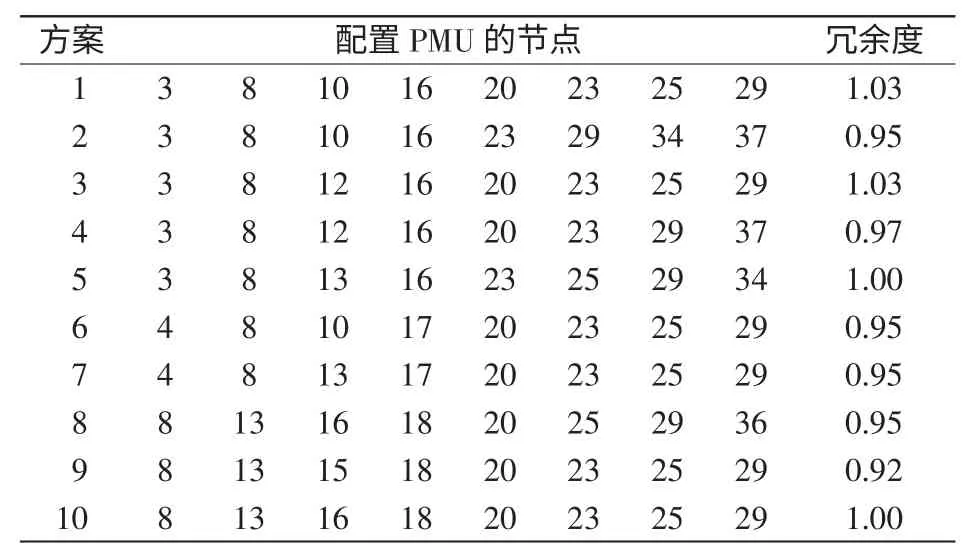
表2 变权重蛙跳法求解New England 39 母线系统配置方案Tab.2 Optimal placement scheme of PMU for New England 39-bus system by VWFLA

方案1 的配置方式见图2，通过优化配置，选择关联支路数较多的母线配置PMU，有效提高了观测冗余度和量测精度，需要8 个PMU 即可达到系统完全可观测。

4.2 算例2

IEEE 57 母线系统结构简化图见图4，算法比较结果见表3，收敛效果比较如图5 所示。

由表3 可知，利用概率偏移粒子群法和原蛙跳算法均未能得出最少配置11 台PMU 的最优方案。而本文所提变权重蛙跳算法可在求得最优解的同时还可提供多种配置方案。由图5 可以看出，本文算法在收敛性方面也更优于另外2 种算法。

利用变权重蛙跳算法求得的3 种最优配置方案如表4 所示，结果中可优选冗余度较大的2 号方案。方案2 的配置方式如图4 所示，需要配置11个PMU 即可达到系统完全可观测。相比其它方案，方案2 在关联支路数较多的6 号和19 号母线配置PMU，明显提高了系统观测冗余度。

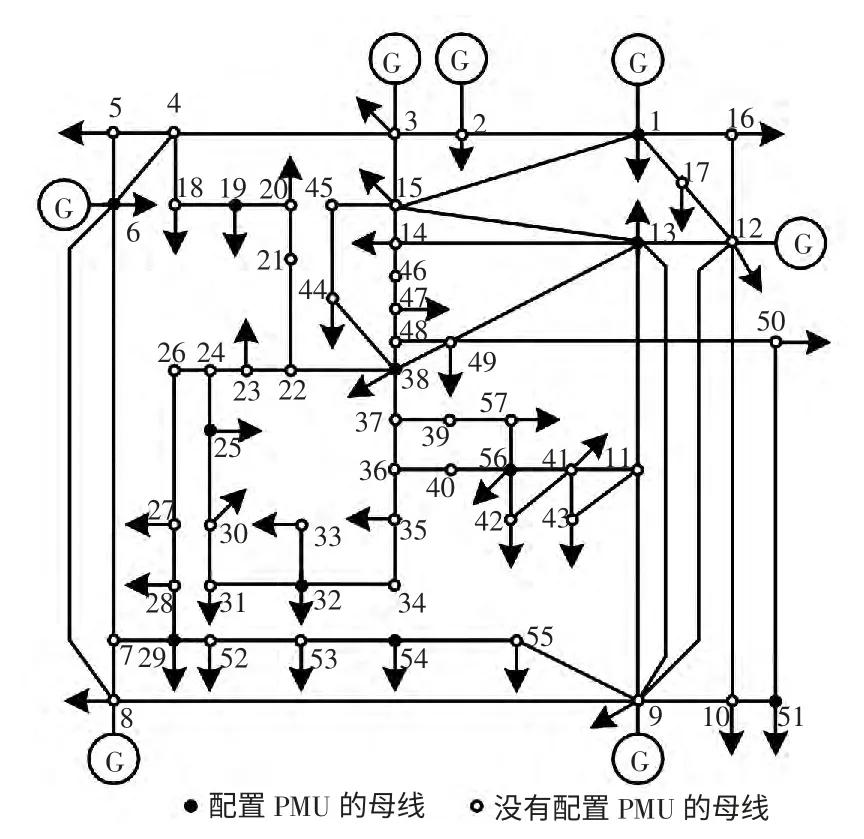
图4 IEEE 57 母线系统简化图Fig.4 Simplified diagram of IEEE 57-bus system

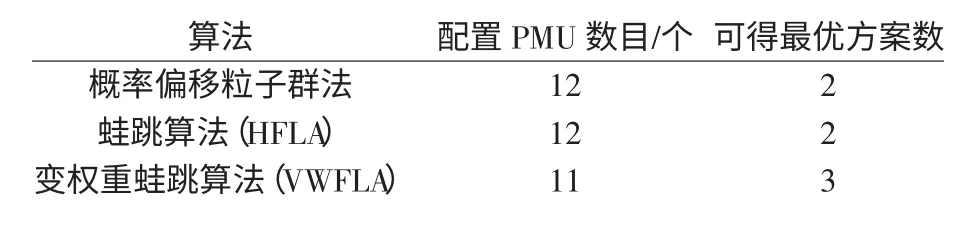
表3 几种算法比较（算例2）Tab.3 Comparison of several algorithms（case 2）

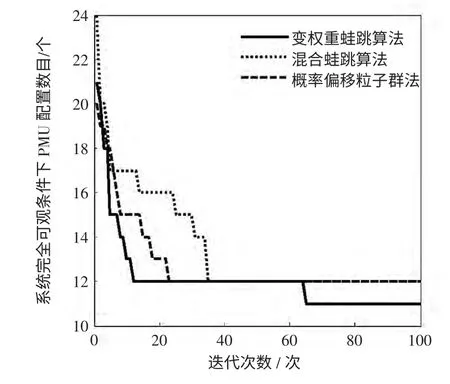
图5 IEEE 57 母线系统变权重蛙跳算法、混合蛙跳算法和概率偏移粒子群法的收敛效果对比Fig.5 Comparison of VWFLA，HFLA and PBPSO for IEEE 57-bus system

表4 变权重蛙跳法求解IEEE 57 母线系统配置方案Tab.4 Optimal placement scheme of PMU for IEEE 57-bus system by VWFLA

由以上2 个仿真算例可知，变权重蛙跳算法与其他常用优化算法相比，更善于解决复杂网络的PMU 配置问题。算法在保证求得最优解的同时具有更好的收敛速度，并可以给决策者提供更多可行的PMU 配置方案。复杂算例也验证了这一结果。

5 结语

针对电力系统PMU 优化配置问题，本文提出应用一种变权重蛙跳算法来求解。通过算例仿真验证，本文算法具有更高计算收敛速度和全局性，并具有最优方案多样化的特点。通过不同算例比较分析，本文算法在分析多节点复杂网络的PMU优化配置问题时更能体现其优势。

[1]Phadke A G.Synchronized phasor measurements in power systems[J].IEEE Computer Applications in Power，1993，6（2）：10-15.

[2]刘斌，黄纯，李波，等（Liu Bin，Huang Chun，Li Bo，et al）.改进二进制粒子群算法在PMU 优化配置中的应用（Application of improved binary particle swarm optimization algorithm in PMU placement）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2010，22（2）：5-10.

[3]田伟，王洪希，孙铁军（Tian Wei，Wang Hongxi，Sun Tiejun）.基于改进遗传模拟退火算法的PMU 优化配置（PMU optimization configuration based on improved genetic simulated annealing algorithm）[J]. 华东电力（East China Electric Power），2007，35（11）：78-81.

[4]彭疆南，孙元章，王海风（Peng Jiangnan，Sun Yuanzhang，Wang Haifeng）. 考虑系统完全可观测性的PMU 最优配置方法（An optimal PMU placement algorithm for full network observability）[J]. 电力系统自动化（Automation of Electric Power Systems），2003，27（4）：10-16.

[5]王茜，张粒子，舒隽，等（Wang Qian，Zhang Lizi，Shu Jun，et al）.基于阈值选择策略的改进混合蛙跳算法在电网规划中的应用（Application of improved shuffled frog leaping algorithm based on threshold selection strategy in transmission network planning）[J].电力系统保护与控制（Power System Protection and Control），2011，39（3）：34-39.

[6]彭春华（Peng Chunhua）.基于免疫BPSO 算法与拓扑可观性的PMU 最优配置（Optimal PMU placement based on immune BPSO algorithm and topology observability）[J].电工技术学报（Transactions of China Electrotechnical Society），2008，23（6）：119-124.

[7]周跃伟，蒋建东（Zhou Yuewei，Jiang Jiandong）. 电力系统中基于MMT 算法的PMU 配置应用研究（PMU disposition research in power system based on MMT algorithm）[J].电力系统保护与控制（Power System Protection and Control），2010，38（4）：74-77.

[8]房大中，王建明，锺德成（Fang Dazhong，Wang Jianming，Chung Takshing）.PMU 最优配置问题的混合优化算法（Hybrid optimization algorithm for optimal phasor measurement unit placement）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2008，20（1）：95-100.

[9]代永强，王联国（Dai Yongqiang，Wang Lianguo）.带记忆功能的混合蛙跳算法（Shuffled frog leaping algorithm with memory function）[J].计算机工程与设计（Computer Engineering and Design），2011，32 （9）：3170 -3173，3202.

[10]Thai-Hoang Huynh.A modified shuffled frog leaping algorithm for optimal tuning of multivariable PID controllers[C]//IEEE International Conference on Industrial Technology.Chengdu，China：2008.

[11]Liu Junwan，Li Zhoujun，Hu Xiaohua，et al.Multiobjective optizition shuffled frog-leaping biclustering[C]//IEEE International Conference on Bioinformatics and Biomedicine Workshops.Atlanta，USA：2011.

[12]骆剑平，李霞，陈泯融（Luo Jianping，Li Xia，Chen Minrong）.混合蛙跳算法的Markov 模型及其收敛性分析（The Markov model of shuffled frog leaping algorithm and its convergence analysis）[J].电子学报（Acta Electronica Sinica），2010，38（12）：2875-2880.

[13]许金元（Xu Jinyuan）.混合型蛙跳算法及其应用研究（Novel frog-leaping algorithm and its application）[J]. 计算机应用研究（Application Research of Computers），2011，28（8）：2835-2837.

[14]Makram E，Zheng Zhao，Girgis A. An improved model in optimal PMU placement considering sensitivity analysis[C]//IEEE/PES Power Systems Conference and Exposition，Phoenix，USA：2011.

[15]王艳松，韩美玉，谭志勇（Wang Yansong，Han Meiyu，Tan Zhiyong）.基于遗传算法的PMU 配置对谐波状态估计质量影响的研究（Study on the effect of PMU allocation on the quality of harmonic state estimation）[J]. 电力系统保护与控制（Power System Protection and Control），2010，38（21）：233-236，240.

[16]程涛，黄彦全，申铁（Cheng Tao，Huang Yanquan，Shen Tie）.遗传算法在PMU 优化配置中的应用（Application of genetic algorithm in optimizing the configuration of PMU）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2009，21（1）：48-51.

[17]张明光，赵金亮，王维洲，等（Zhang Mingguang，Zhao Jinliang，Wang Weizhou，et al）.基于自适应遗传算法和蚁群算法融合的配电网重构（Distribution network reconfiguration based on the combination of adaptive genetic algorithm and ant colony algorithm）[J]. 电 气 自 动 化（Electrical Automation），2011，33（6）：57-60.

[18]吴秀华，朴在林，徐静，等（Wu Xiuhua，Piao Zailin，Xu Jing，et al）.基于改进粒子群优化算法的电力系统无功电压综合控制（Reactive power and voltage control based on improved particle swarm optimization in power system）[J].继电器（Relay），2007，35（21）：28-33，38.