黑龙江省小兴安岭北坡林分生长率模型的建立

郑春华，高振寰，杨胜涛

（1.黑龙江省林业监测规划院，黑龙江 哈尔滨150080；2.黑龙江省林业厅，黑龙江 哈尔滨150090）

掌握正确的森林生长规律是森林资源科学管理的基础。各林分和树种的生长率是林业生产经营的重要定量指标，是编制林业规划、经营方案，确定采伐限额，实行森林集约经营的重要依据。本次编表采用黑龙江省小兴安岭北坡的白桦林、柞树林、黑桦林、软阔叶混交林等主要林分类型样地监测数据，探索林分生长率表的编制方法。

1 基础数据的来源

林分生长率表编表数据和检验数据均来源于1997年、2006年、2007年、2009年、2010年、2011年的森林资源县级监测样地数据和国家重点生态公益林监测样地的复位样地数据。各林分生长率表编表检验数据来源于2012年国家重点生态公益林监测样地的复位样地数据。

2 数据的收集和整理

通过定量与定性相结合的综合分析方法，剔除了样地变化较大、样木生长不正常、外业测定有误的数据。对整理后的数据录入微机，建立编制生长率表数据库，作为编表工作的基础。

2.1 收集数据

为了编制黑龙江省小兴安岭北坡主要林分生长率表，将小兴安岭北坡森林资源监测样地进行了整理，并重新计算了复位的有林地样地蓄积量和各株样木的材积，并分别计算出了各样地的生长率和各样木生长率。其中复位样地3 327块，年复位样木120 890株。见表1。

表1 林分生长率表样本数量统计 个

2.2 数据整理

将上述不同优势树种（组）分别进行统计后，建立不同优势树种（组）各林分年龄所对应的生长率的数据库，然后分别计算出各个林分年龄的平均生长率和标准差，以2倍标准差为临界值，对数据进行筛选，剔除异常数据。同时将数据库随机分成两组独立样本：编表样本和检验样本。

经检验各树种的编表数据和验表数据各年龄株数的分布近似正态分布，符合编表要求。见表2。

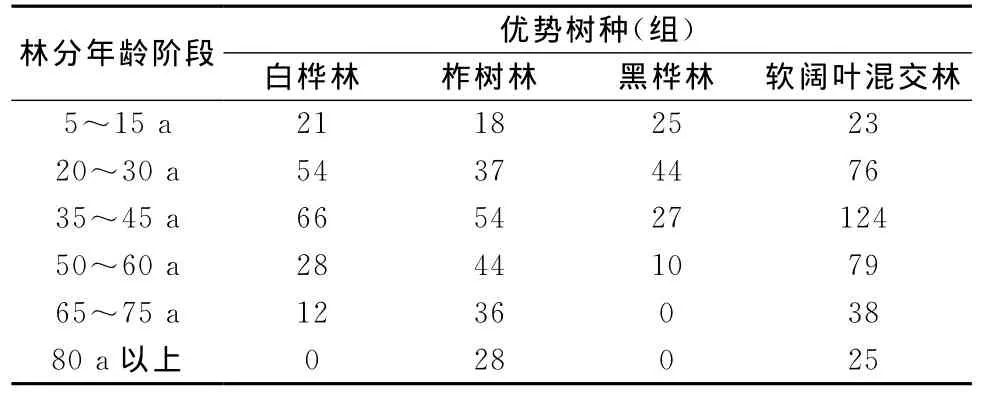
表2 编表数据和验表数据年龄阶段分布 个

3 林分生长率表编制

3.1 林分生长率表编制的方法

3.1.1 相关计算公式

林分总生长率公式：PZ＝（Vb－Va＋M0＋C）×2／［（Vb＋Va）×N］×100

林分净生长率公式：Pj＝ （Vb－Va＋C）×2／［（Vb＋Va）×N］×100

式中，Pz—林分总生长率（%）；Pj—林分净生长率（%）；Va—林分期初蓄积（m3）；Vb—林分期末蓄积（m3）；M0— 林分枯损蓄积（m3）；C—林分采伐蓄积（m3）；N—间隔期。

3.1.2 林分年龄的确定 根据生长率的计算公式，其生长率是指林分从N年至N＋A年之间的生长率，所以，将生长率所对应的年龄确定为复位样地间隔期中间年龄。

3.1.3 林分龄组的划分 将林分年龄加上1／2间隔期作划分林分龄组的年龄，按照黑龙江省重点公益林监测操作细则龄组划分标准确定龄组。

3.2 方程拟合结果及参数检验

根据各样地林龄和生长率的散点图，结合国内外的编表经验，确定y＝a＋blnx为林分总生长率和净生长率的回归方程式，应用SPSS14.0软件对其进行拟合，得出其回归模型的参数进而得出回归模型。根据回归模型计算出该林分各整数年龄的理论生长率，然后根据林分龄组划分标准，通过加权平均的方法计算出各龄组的生长率。

对方程y＝a＋blnx（y—林分生长率，x—林分年龄），在估计数学模型参数的同时，在α＝0.05的显著水平下，理论t值为1.96。spss14.0求出了该数学模型的各种拟合统计量：剩余离差平方和（RSS）、相关系数（r2），回归显著性检验（F检验）结果及偏回归系数的显著性检验（t检验）结果等的相关指标值。见表3。

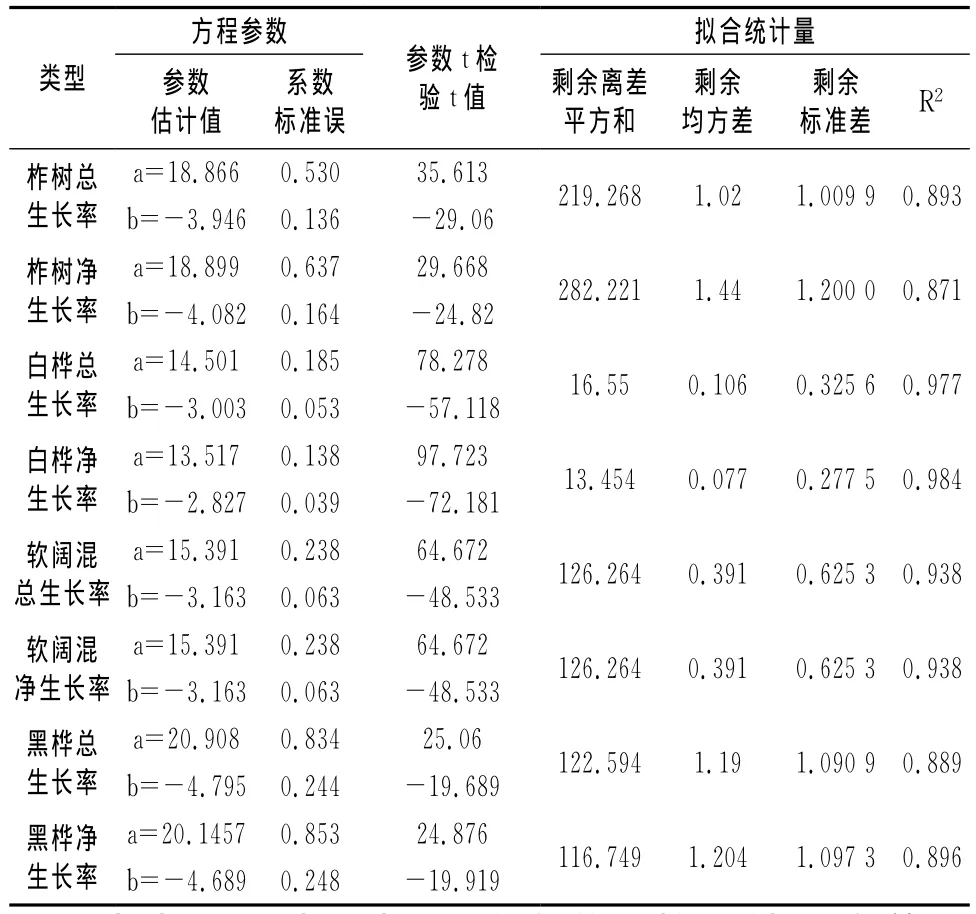
表3 林分生长率回归方程参数及参数检验结果

由表3可以看出，两个参数t检验结果均差异显著，表明回归模型相关显著。

3.3 林分生长率回归模型的精度

采用独立检验数据，对小兴安岭北坡林分生长率模型进行了误差、预估精度分析。包括：平均误差、平均绝对误差、平均相对误差、平均绝对相对误差、系统误差、精度。见表4。

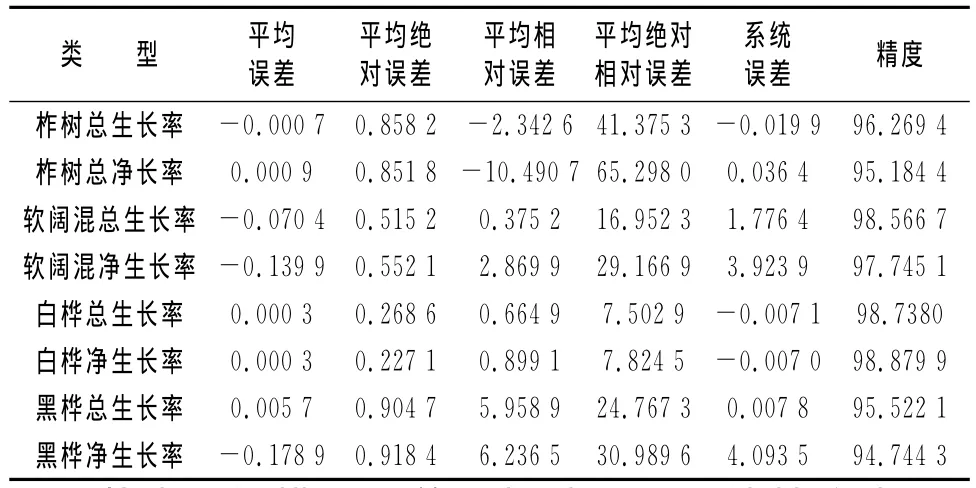
表4 林分生长率模型检验结果

从表4的模型误差分析结果及预估精度来看，无论是平均误差、绝对平均误差和系统误差还是预估精度，两者相差无几。系统误差小于±5%，模型预估精度不低于95%。这表明所建模型满足精度要求，可以在生产中推广使用。

［1］白云庆，郝文康.测树学［M］.哈尔滨：东北林业大学出版社，1997

［2］陈华豪，丁恩统.林业应用数理统计学［M］.大连：大连海运学院出版社，1988