线性规划的教学模式探讨

苗连英，逄世友

（中国矿业大学　理学院，江苏　徐州　221008）

线性规划的教学模式探讨

苗连英，逄世友

（中国矿业大学理学院，江苏徐州221008）

线性规划是运筹学的核心内容，求解线性规划的单纯形法在理论上已趋于成熟，应用也越来越广泛。为了使学生更容易、更深刻地理解这种算法及其理论基础，本文给出了一种循序渐进的教学模式。这种模式也适用于运筹学其他内容的教学。

单纯形法；循序渐进；教学模式

运筹学是二战期间发展起来的一门应用学科，它广泛应用现有的科学技术知识和数学方法，解决实际中提出的一些问题，为决策者选择最优策略提供定量依据，其内容包括：规划论（线性规划、非线性规划、整数规划、动态规划、多目标规划等）、图论与网络分析、对策论、排队论、存储论、决策论、排序与统筹方法等[1]。运筹学的实际应用涉及生产计划、运输问题、人事管理、库存管理、市场营销、财务和会计等方面。另外，还应用于设备维修、更新和可靠性分析，项目的选择与评价、工程优化设计、环境保护等问题中。据统计，50%数学建模问题与运筹学内容相关，可以用运筹学的方法解决。另外，为各大高校数次争得荣誉的建模队伍，长期以来一直接受运筹学相关知识的培训。

运筹学中最主要的分支是线性规划。线性规划模型是前苏联著名经济学家康托罗维奇于1939年提出的，这一重大发现使他获得了诺贝尔经济学奖。1947年G.B.Dantzig提出求解线性规划的单纯形法。针对退化问题，1952年A.Charner和W.W.Cooper[2]给出了摄动法，1954年G.B.Dantzig，A.Orden和P.Wolfe[3]提出了字典序方法，1976年G.G.Bland[4]提出了Bland法则，这些方法都能避免循环发生。线性规划理论上已趋于成熟，应用也越来越广泛。事实上，运筹学中许多问题都可以或需要用线性规划模型来描述或近似地描述，如运输问题——求解运输问题的表上作业法本质上就是单纯形法，并且这种方法充分展示了单纯形法的魅力。求最短路、最小费用最大流的问题都可以用线性规划模型来解决。求解指派问题的匈牙利法本质上也是单纯形法[5]。矩阵对策问题最后转化成求解线性规划。学习运筹学的先修课程主要有线性代数、微积分、概率论与数理统计。事实上，运筹学不仅应用了这些学科，也从理论上进一步发展了这些学科。

单纯形法是建立在一系列理论基础之上的。首先，如果线性规划的可行域非空，则它是一个凸集，这个结论很容易证明。线性规划的可行域的顶点与基可行解之间是一一对应的，所以其顶点个数有限，这个结论与单纯形法的关系不大，其证明可以省略。其次，线性规划若有可行解，则一定有基可行解，这个结论是很重要的，为了更好地理解它的证明，我们先看下面的例子。

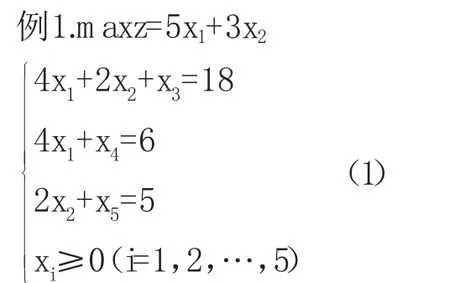
任意找出该线性规划的一个可行解，比如X0=（1，1，12，2，3）T。由于其正分量的个数大于3，所以它不是基可行解。如何找出一个基可行解呢？由（1）可知P1-P2-2P3-4P4+2P5=0，令α=（1，-1，-2，-4，2）T.

设t是一个很小的正数，构造两个向量：

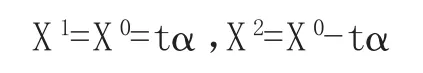
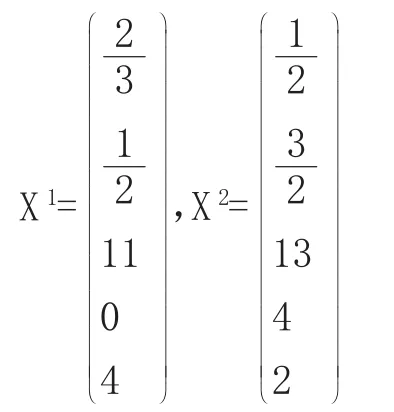
首先注意到AXi=A（X0±tα）=AX0±tAα=b.另外我们要取适当的t，使得X1≥0，X2≥0.通过观察上面两式可知时，X1和X2都是可行解。取得，

进一步讲，若线性规划有最优解，其最优解一定可以在其可行域的顶点上找到，也就是在其基可行解中找到，这样就把一个从无限个可行解中找最优转化成在有限个可行解中找最优。这是单纯形法的理论基础。为了更好地理解这一重要结论的证明，我们看下一个例子。

X0=（1，2，0，1）T是（2）的一个最优解，由于其正分量的个数大于2，所以它不是基可行解。下面找一个基可行解也是最优解，方法与例1类似。由（2）可知2P1-P2-P4=0，令α=（2，-1，0，-1）T.

设t是一个很小的正数，构造两个向量：

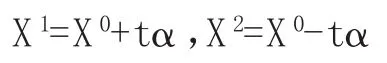
首先注意到AXi=A（X0±tα）=AX0±tAα=b。另外我们要取适当的t，使得X1≥0，X2≥0。通过观察上面的式子可知时，X1和X2都是可行解。

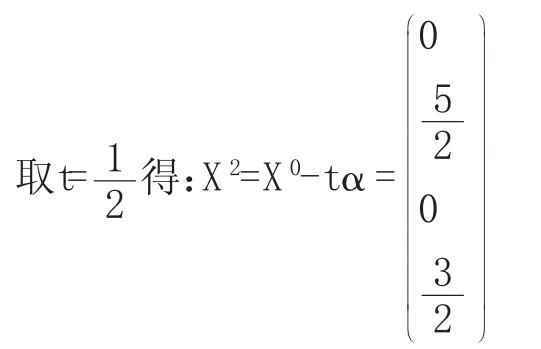
而且有CX0≥CX1，CX0≥CX2，即CX0+tCα=CX1≤CX0，CX0-tCα=CX2≤CX0.从而Cα=0，即X1和X2都是最优解。X2的正分量的个数是2。由于P2，P4线性无关，所以X2是基可行解。这样我们就找到了一个最优解也是基可行解。一般地，若X2的正分量对应的系数列与线性相关，继续上述过程，直到找到基可行解为止。

从基可行解中找最优解所用的方法是单纯形迭代法。那么，如何判断一个线性规划是否有最优解？如何判断一个基可行解是否是最优解？在一个基可行解不是最优的情况下如何迭代到下一个与其相邻的更好的基可行解？为回答这些问题，我们举例说明。

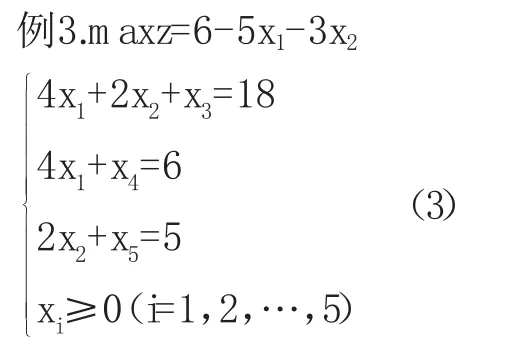
该问题有一明显的基可行解X0=（0，0，18，6，5）T，且（3）就是X0对应的典式，由于x1，x2的价值系数都小于0，从而X0是最优解，且是唯一的最优解。因为若还有另一个最优解则必有，从而即X0=X1.

把上例稍作修改，如下例：

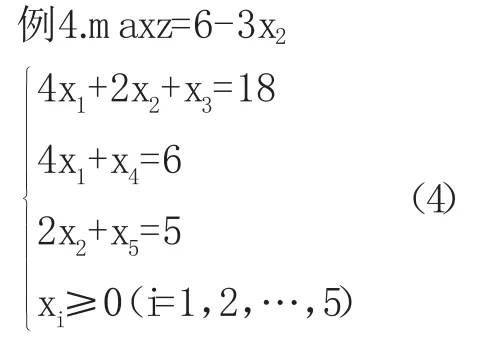
X0是（4）的基可行解。由于x1的价值系数是0，所以只要保持x2=0，x1的增加不会改变z的值。由约束方程组可知，x1可取中的任何值。当时，可得另一最优解，X0的X1任意凸组合都是最优解，从而该问题有无穷多最优解。

再看下例：

X0是（5）的基可行解，但不是最优解，因为只要x1增大，z就会增大。若令x2=0，则约束方程组变成：

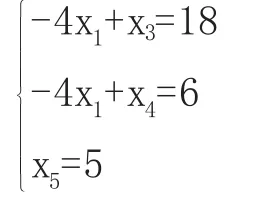
令x1=θ＞5，则得一个可行解X=（θ，0，18+4θ， 6+4θ，5）T，其对应的由此可知，该问题无最优解或有无界解。

通过例3~例5可以引出最优性判别定理：

设X0是基可行解，其对应典式为：

①如果对一切j=m+1，…，n，有σj≤0，则X0是线性规划的最优解。

②如果对一切j=m+1，…，n，有σj＜0，则X0是线性规划的唯一最优解。

③如果对一切j=m+1，…，n，有σj≤0，且存在某个σm+k=0，则线性规划有无穷多最优解。

④若存在某个σm+k＞0，且对一切i=1，2，…，m，有βi，m+k≤0，则线性规划无最优解（最优值为无穷大）。

再看一个例子：

X0是（6）的基可行解，但不是最优解，因为当x1、x2增大时，z也会增大。注意我们只能让x1、x2之一增大，这样才能得到一个与X0相邻的基可行解。由于x1的价值系数比x2的价值系数大，我们一般是让x1增大，x2还是0。

由于x1最大可以增大到，从而得到新的基可行解：

这里需要说明X1还是基可行解，只要证明P1，P2，P3线性无关即可。由于P1，P3，P4与P3，P4，P5等价（容易看出，从而X1也是基可行解。通过变换求出X1对应的典式，完成一次单纯形迭代。

通过上例可以引入基可行解的改进定理：

设X0是基可行解，其对应典式如（6）：

①若存在某个σm+k＞0.

②存在i∈{1，2，…，m}，使得βi，m+k＞0.

③所有的αi＞0，i∈{1，2，…，m}，则一定存在另一个基可行解X1，使得CX0＜CX1。

进而提出单纯形算法的基本步骤：

①找出一个初始基可行解X0，写出X0相应的典式。

②如果所有非基变量xj的检验数都不大于0，则X0是最优解，计算结束，否则转至③。

③取一个最大的检验数σk＞0，如果所有的βik≤0，则线性规划问题无最优解，计算结束，否则转至④。

则xk为换入变量，xl为换出变量，得到一个新的基可行解X1，转⑤。

⑤进行基变换，得到X1的典式，转②。

先讲特例再引入最优性判别定理、基可行解的改进定理以及单纯形法的迭代步骤，学生就容易理解。即使针对有些专业的学生讲解这些定理的证明，也容易接受。

总之，现代社会信息量大，大学生需要学习的课程很多，用于预习或复习的时间就很少，这样上课时间就尤为珍贵，教师应该如何讲，才能使学生当堂听明白所授内容，这是一个必须思考的问题。其实，运筹学这门学科更侧重的是应用，数学理论并不难，之所以有人觉得难学，是因为没有把握一种好的学习方法。本文针对单纯形法给出了一种循序渐进的教学模式，实践证明这种模式能使学生更容易的理解课堂内容，有利于激发学生的自信心和学习兴趣，使学生在轻松掌握数学理论的基础上，能更好地探讨运筹学的经典案例的建模和求解，加强学生运用所学知识解决实际问题的能力和创新能力。

[1]《运筹学》教材编写组.运筹学[M].北京：清华大学出版社，2004.

[2]Charnes，A.And CooperW.W.，The stepping stonemethod of explaining linear programm ing calculations in thansportation problems，ManagementScience，1954，（1）：49-69.

[3]Dantzig，G.B.，O rden.A.and W olfe.P.，Note on linear programm ing，Pacific J.Math.1955，（5）：183-195.

[4]Bland，G.G.，New finite pivoting rules of Simplex method，Math.O fOperationsResearch，1977，（2）：103-107.

[5]Hamdy，A.Taha，Operations Research-An Introduction[M].北京：人民邮电出版社，2007.

G642.0

A

1674-9324（2014）45-0036-04

2014年度江苏省研究生教育教学改革研究与实践课题，《运筹学》立体化教学平台建设；2014年中国矿业大学精品资源共享课：《运筹学》

苗连英（1966-），女，中国矿业大学理学院教授，主要从事运筹学教学和科研工作。