A Matrix Formulation of Discrete Chirp Fourier Transform Algorithms

Juan Pablo Soto Quiros and Domingo Rodriguez

A Matrix Formulation of Discrete Chirp Fourier Transform Algorithms

Juan Pablo Soto Quiros and Domingo Rodriguez

—This work presents a computational matrix framework in terms of tensor signal algebra for the formulation of discrete chirp Fourier transform algorithms. These algorithms are used in this work to estimate the point target functions (impulse response functions) of multiple-input multiple-output (MIMO) synthetic aperture radar (SAR) systems. This estimation technique is being studied as an alternative to the estimation of point target functions using the discrete cross-ambiguityfunctionforcertaintypesof environmental surveillance applications. The tensor signal algebra is presented as a mathematics environment composed of signal spaces, finite dimensional linear operators, and special matrices where algebraic methods are used to generate these signal transforms as computational estimators. Also, the tensor signal algebra contributes to analysis, design, and implementation of parallel algorithms. An instantiation of the framework was performed by using the MATLAB Parallel Computing Toolbox, where all the algorithms presented in this paper were implemented.

Index Terms—Discrete chirp Fourier transform, MATLAB, parallel computing, tensor signal algebra.

1. Introduction

This work deals with the fundamental issue of fast and efficient treatment of microwave remote sensed data of objects modeled as point targets in order to extract information important to a surveillance user. Great advances in active sensor technology, communications, and signal processing technology are demanding new computational theories and methods to improve our rapid awareness of our physical sensory reality. For the particular case of synthetic aperture radar (SAR) systems[1], this implies the need for faster and efficient means for signal intelligence.

The work presents here concentrates on the formulation of a computational matrix framework in terms of tensor signal algebra, which is as a set consisting of signal spaces, operators, and special matrices for algebraic modeling of point target response functions using point estimates of discrete chirp Fourier transforms (DCFTs) of echo returns modeled as multi-component polynomial phase signals. The tensor signal algebra has been demonstrated to be instrumental in the analysis, design, and implementation of different classes of algorithms for SAR computational signal processing applications[2]-[4].

We concentrate our effort on the matrix formulation of algorithms for the computation of discrete chirp Fourier transforms. This computational matrix framework allows the systematic study of variants of discrete chirp Fourier transforms formulations under a unified setting, which is considered as one of the major contributions of this work. Also, an instantiation of this computational matrix framework was implemented by using the MATLAB Parallel Computing Toolbox.

The paper is organized as follows. In Section 2, we explain preliminaries concepts: matrix notations, tensor signal algebra definitions, and the definition for the discrete Fourier transform operator. In Section 3, we describe the different DCFTs definitions. In Section 4, we develop a matrix formulation for DCFTs algorithms using tensor signal algebra. Also, a proof of DCFTs matrix inverses is developed. In Section 5, we provide an implementation of DCFT algorithms using the MATLAB Parallel Computing Toolbox. Finally, we present our conclusions in Section 6.

2. Preliminaries

2.1 Matrix Notation

2.2 Tensor Signal Algebra

In this paper, we define tensor signal algebra as a mathematics environment composed of signal spaces, operators, and special matrices where algebraic methods are used to develop algorithms to perform signal processing operations. Also, the tensor signal algebra contributes to analysis, design, and implementation of parallel algorithms for signal processing applications. Now, we proceed to define some operators and matrices associated with tensor signal algebra.

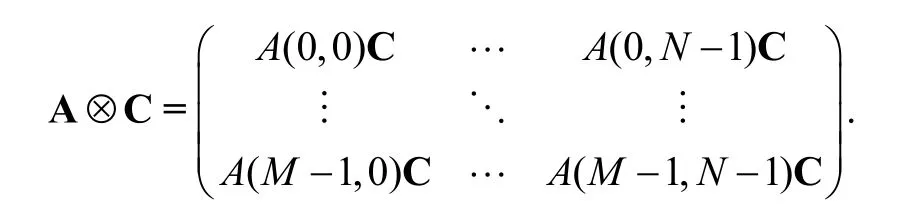
Let N RS= , the stride permutation matrix,permutes the elements of the input vectorasThe vector operator,transforms a matrix of dimension M N× into a vector of dimensionMN, by stacking, in order, all the columns of this matrix one underneath the other. The vector inverse operator,, transforms a vector of dimension MNinto a matrix of sizethenis the matrix indefined by

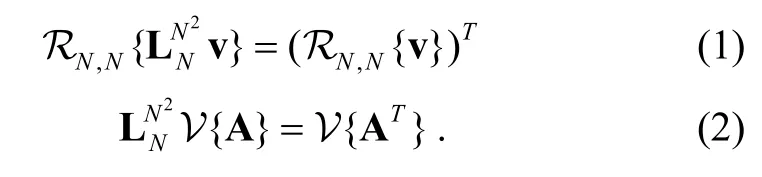
The operators and matrices mentioned above have been used in several research associated with signal processing in [2], [3], and [5]-[10].

2.3 Discrete Fourier Transform

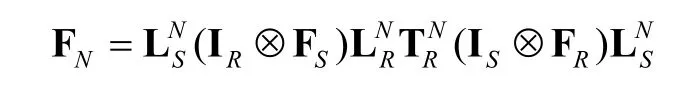
3. Discrete Chirp Fourier Transform

DCFT defined by Xia in [11] matches the multiple chirp rates in a chirp-type signal with multiple chirp components. Also, the DCFT can be used to transform signals that are not sparse in either time or frequency, such as linear chirps, into sparse signals[12].. The DCFT ofxis defined as the map with domainand co-domain ℂ. Here, we formulate three types of DCFTs definitions:

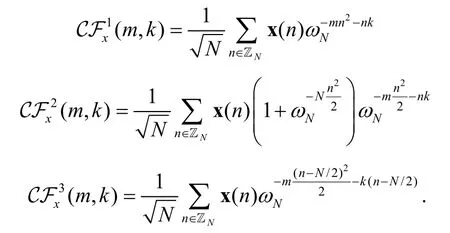
When the signal length is prime, the magnitudes of all the sidelobes of the DCFT-1 of a quadratic chirp signal are 1, whereas the magnitude of the mainlobe of the DCFT-1 isWhen the signal length is12N N= ,1N prime, the magnitudes of all the sidelobes of the DCFT-2 of a quadratic chirp signal arewhereas the magnitude of the mainlobe of the DCFT-2 isWhen the signal length isprimes, the magnitudes of all the sidelobes of the DCFT-3 of a single chirp signal are N1,N2or 1, whereas the magnitude of the mainlobeof the DCFT-3 isthen the DCFT-1, DCFT-2, and DCFT-3 can be represented as:

4. Matrix Formulation of DCFTs

The DCFTs are bi-dimensional functions and we can express each of them as a matrix. Forthe DCFT-nis defined asThe following theorem formulates the DCFTs matrices using tensor signal algebra.

Proof: We provide a proof ofThe proofs ofare similar.

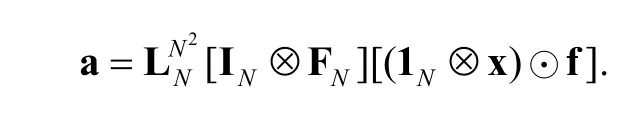
Multiplying the parentheses, we obtain

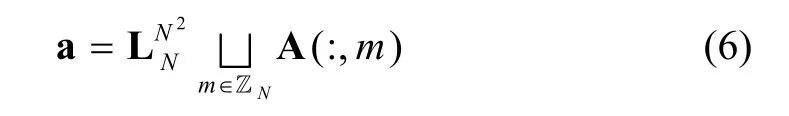
such that

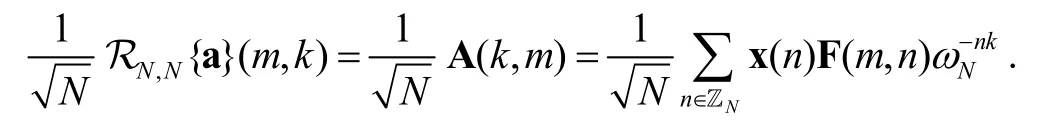
A study of the inverse of DCFT-1 was developed in [11] and [15]. Now, we present an alternative proof for the DCFT-1 inverse and the DCFT-3 through matrix representations.

Then,

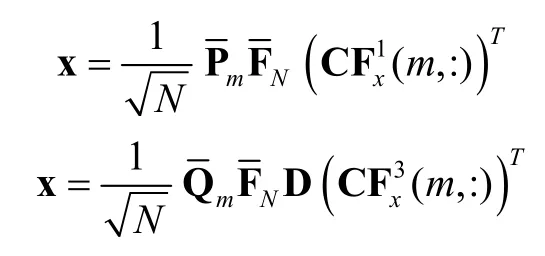
Proof. We provide a proof forThe proof foris similar. For fixedand from (3), we obtain a system of linear equations of order N. The matrix representation of this system is shown in (8) and (9). From the coefficient matrixM, we obtainandare invertible, we then have

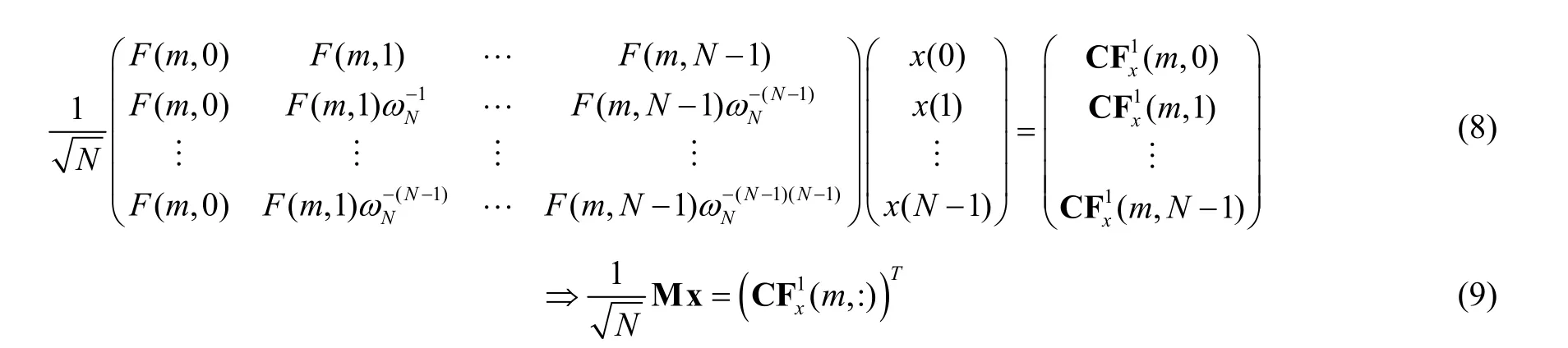
The DCFT-2 is not invertible, because it is not injective (see Appendix B). However, Theorem 3 will obtain the best signal approximation for the original signal, such that the norm-2 of the signal approximation is less than norm-2 of the original signal.

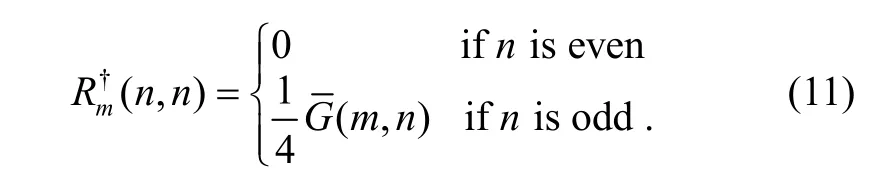
Proof. Similarly to the proof of Theorem 2, we obtain

5. Implementation of DCFT Algorithms with Parallel Computing Toolbox™

Owing to the close relation between DFT and DCFTs, Theorem 1 presents the matrix representation of DCFTs. Also, asis called parallel operation[2], the implementation of DCFTs can be performed by using parallel computing. From Theorem 1, the DCFT-1 matrix can be computed in parallel, since each (:,)mAof (7) can be computed independently and in parallel.

In this paper, we perform an implementation of DCFTs using the MATLAB Parallel Computing Toolbox, through the basic command parfor, as shown in below. The parfor divides the loop iterations into groups so that each lab executes in parallel some portion of the total number of iterations. Here, a lab is an independent instance of MATLAB that runs separately.

% DCFT-1: An implementation in parallel MATLAB

N=67; w=exp(2*pi*1i/N); t=0:N-1; C=zeros(N);

m0=25; k0=30; m1=5; k1=63;

x=w.ˆ(m0*t.ˆ2+k0*t) + w.ˆ(m1*t.ˆ2+k1*t);

matlabpool open 2

parfor m=0:N-1

f=w.ˆ(-m*t.ˆ2); v=x.*f;

C(:,m+1)=fft(v);

end

C=C.’;

matlabpool close

surface(t, t, abs(C)).

6. Conclusions

This work presented a computational matrix framework for the formulation of DCFTs algorithms by using the tensor signal algebra. An instantiation of the framework was performed by using the Parallel Computing Toolbox™of Matlab®, where all the algorithms presented in this work were implemented.

Appendix A: Pseudocodes of DCFTs Algorithms

Algorithm 1: DCFT-1 Algorithm

2. (,:)m←vF(see (3) for(,:)mFvalues)

3: ←fxv⊙

5: end for

Algorithm 2: DCFT-2 Algorithm

2. (,:)m←vG(see (4) for (,:)mGvalues)

3: ←gxv⊙

5: end for

Algorithm 3: DCFT-3 Algorithm

2. (,:)m←vH(see (5) for (,:)mΗvalues)

3: ←hxv⊙

5: end for

6: ←Ddiagonal matrix such that (,) (1)nD n n=-

Appendix B: Auxiliary Result

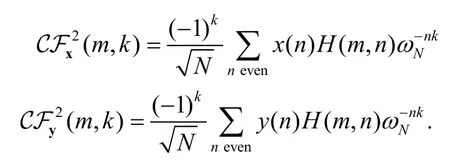
[1] G. Krieger, N. Gebert, and A. Moreira, “Multidimensional waveform encoding: A new digital beamforming technique for synthetic aperture radar remote sensing,” IEEE Trans. on Geoscience and Remote Sensing, vol. 46, no. 1, pp. 31-46, 2008.

[2] D. Rodriguez, “A computational kronecker-core array algebra SAR raw data generation modeling system,” in Proc. of the Thirty-Fifth Asilomar Conf. on Signals, Systems and Computers, Pacific Grove, 2001, pp. 116-120.

[3] J. Johnson, R. Johnson, D. Rodriguez, and R. Tolimieri, “A methodology for designing, modifying, and implementing Fourier transform algorithms on various architectures,” Proc. of Circuits, Systems, and Signal Processing, vol. 9, no. 4, 1990, pp. 449-500.

[4] P. M. Woodward, Probability and Information Theory, With Applications to Radar, New York: McGraw-Hill, 1953.

[5] C. V. Loan, Computational Framework for the Fast Fourier Transform, Philadelphia: SIAM, 1992.

[6] B. Yang, “A study of inverse short-time Fourier transform,”in Proc. of IEEE Int. Conf. on Acoustics, Speech and Signal Processing, Las Vegas, 2008, pp. 3541-3544.

[7] F. Franchetti, M. Püschel, Y. Voronenko, S. Chellappa, and J. M. F. Moura, “Discrete Fourier transform on multicore,”IEEE Signal Processing Magazine, vol. 26, no. 6, 2009, pp. 90-102.

[8] M. An, A. K. Brodzik, and R. Tolimieri, Ideal Sequence Design in Time-Frequency Space, Berlin: Birkhäuser Basel, 2009.

[9] D. Marquez, J. Valera, A. Camelo, C. Aceros, M. Jimenez, and D. Rodriguez, “Implementations of cyclic crossambiguity functions in FPGAs for large scale signals,” in Proc. of IEEE Second Latin American Symposium on Circuits and Systems, Bogotá, 2011, pp. 1-4.

[10] J. P. S. Quiros and D. Rodriguez, “Representación matricial de algoritmos en paralelo de la transformada discreta de fourier, la función discreta de ambigüedad y la distribución discreta de Cohen,” La Gaceta, vol. 16, no. 3, pp. 479-500, 2013.

[11] X.-G. Xia, “Discrete chirp-Fourier transform and its application to chirp rate estimation,” IEEE Trans. on Signal Processing, vol. 48, no. 11, pp. 3122-3133, 2000.

[12] P. Fan and C. Feng, “A new discrete chirp Fourier transform,” in Proc. of the 6th Int. Conf. on Signal Processing, Beijing, 2002, pp. 49-53.

[13] P. Fan and X.-G. Xia, “A modified discrete chirp-Fourier transform scheme,” in Proc. of the 5th Int. Conf. on Signal Processing, Beijing, 2000, pp. 57-60.

[14] A. Ben-Israel and T. Greville, Generalized Inverses: Theory and Applications, Berlin: Springer, 2003.

[15] O. Alkishriwo and L. Chaparro, “A discrete linear chirp transform (DLCT) for data compression,” in Proc. of the 11th Int. Conf. on Information Science, Signal Processing and Their Applications, Montreal, 2012, pp. 1283-1288.

The authors’ photographs and biographies are not available at the time of publication.

Manuscript received April 19, 2013; revised June 31, 2013.

J. P. S. Quiros is with the Department of Mathematics, Costa Rica Institute Technology, 159-7050 Cartago, Costa Rica (Corresponding author e-mail: jusoto@itcr.ac.cr).

D. Rodríguez is with the Department of Electrical and Computer Engineering, University of Puerto Rico, Mayagüez Campus, Mayagüez, PR 00681, USA (e-mail: domingo@ece.uprm.edu).

Digital Object Identifier: 10.3969/j.issn.1674-862X.2014.02.013